E2Par04 - Universidad de Sevilla

Departamento: Física Aplicada III
Escuela Superior de Ingenieros. Universidad de Sevilla
Fundamentos Físicos de la Ingeniería. (Industriales)
Primer parcial (Mecánica) . Curso 2003/2004
Solución del corrector
Ejercicio 2: CINEMÁTICA DEL SÓLIDO RÍGIDO Y VECTORES DESLIZANTES
G
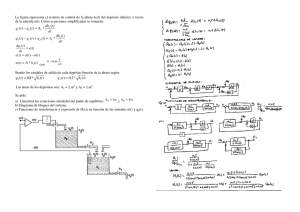
Se sabe que la fuerza infinitesimal dFP que actúa sobre cada punto P de un semianillo rígido, homogéneo, de grosor
despreciable, y situado en el plano horizontal OXY (modelo: semicircunferencia de densidad longitudinal de masa λ, centro
G
G
G
en O y radio R), viene dada por la expresión dFP = aP dm , donde aP es la aceleración de dicho punto, y dm = λ R dθ es el
elemento de masa infinitesimal que lo ocupa. Para la posición representada en la figura, determine:
G
1. la resultante, F ;
G
2. el momento resultante respecto al punto O, M O ;
3. el eje central, ∆C ;
4. y la reducción canónica
del sistema distribuido de fuerzas (vectores deslizantes) que actúa sobre el semianillo, en cada uno de los siguientes
supuestos:
i. El semianillo rota con velocidad angular constante ω alrededor del eje OZ.
G
2
G
ii. El semianillo se traslada con velocidad v(t)=- ω 2 Rt j
π
Y
Consideraciones previas.
P
dm
R
O•
θ
X
•
En cualquiera de los casos pedidos, la figura
corresponde al instante predeterminado en que se desean las
respuestas.
•
La aceleración de cada masa infinitesimal es la del
punto P que ocupa en el semianillo y puede obtenerse
mediante la expresión del campo de aceleraciones del sólido
rígido en cada caso
G
•
Llamaremos F a la resultante del sistema de fuerzas
G
elementales {P; dFP }
Caso i: Rotación uniforme
G
G
G JJJG G G JJJG
a P = a O + α × OP + ω × (ω × OP ) .
G
a O = 0 , porque O pertenece al eje permanente de rotación OZ
α = 0, porque rota con ω constante.
JJJG
G G JJJG
ω × (ω × OP ) = −ω 2 OP
G
G
G
Con lo cual a P = − ω 2 R (cosθ i + senθ j )
JJJG
G
G
G
G
ó
dFP = −ω 2 OP dm
dFP = − ω 2 R (cos θ i + senθ j )λ R dθ
1.
G
Cálculo de la resultante F
G
G
G
G
G
F
π
F = ∫ dFP = ∫ −ω 2 R(cosθ i + sen θ j ) λ R dθ
0
0
G
G
F = −2λ R 2ω 2 j
G
G
G π
F = −λ R 2ω 2  senθ i − cosθ j  0
G
2. Calculo del momento M O
JJJG
JJJG
JJJG
G
G
G
dM O = OP × dFP ; dM O = OP × ( −ω 2 OP dm )
JJJG
G
G
Como OP y dFP , son vectores paralelos, su producto vectorial vale 0 para cualquier punto P. En consecuencia M O = 0
Ejercicio 2
Departamento: Física Aplicada III
Escuela Superior de Ingenieros. Universidad de Sevilla
Fundamentos Físicos de la Ingeniería. (Industriales)
Primer parcial (Mecánica) . Curso 2003/2004
3.
Eje central
G
M O = 0 significa que el momento es mínimo en O y por ello este punto debe pertenecer al eje central del sistema. Además el
eje central posee la dirección de la resultante, es decir OY, luego el eje central de este sistema de vectores deslizantes es el eje
OY.
4.
Reducción canónica
G G
La reducción en un punto Q de un sistema de vectores deslizantes –tres vectores como máximo– se indica por F , M Q donde
G
G
F es la resultante aplicada en el punto Q y M Q representa el momento de un par de vectores de resultante nula, que ha de
{
coincidir con el momento en Q del sistema completo.
}
G G
G
La reducción canónica es la referida a cualquier punto C del eje central y se representa por F , mC , donde mC posee la
G
G
propiedad adicional de ser el momento de módulo mínimo y paralelo a F . En el caso que nos ocupa mC = 0 .
G
En consecuencia el sistema equivale a un solo vector F aplicado en cualquier punto del eje OY.
{
}
G
2
G
Caso ii: Traslación v P = − ω 2 R t j
π
La traslación se caracteriza porque el vector rotación angular vale 0, lo que nos conduce a que todos los puntos del sólido
poseen la misma velocidad y la misma aceleración en cada instante t. Derivando la expresión anterior se obtiene
G
G
2
G P dv P
G
a =
;
aP = − ω2R j
dt
π
1.
G
Cálculo de la resultante F
G
G
2
dFP = − λω 2 R 2 dθ j ;
π
G
G π
2
F = − λω 2 R 2 j ∫ dθ ;
π
G
G
F = − 2λω 2 R 2 j
0
G
Cálculo del momento M O
JJJG
G
G
G
G
G −2
G
π
dM O = OP × dFP ;
M O = ∫ R (cosθ i + senθ j ) × λω 2 R 2 dθ j
2.
π
0
G π
G
−2
MO =
λω 2 R3 k ∫ cos θ dθ ;
π
0
G
−2
π G
MO =
λω 2 R 3 [ senθ ]0 k ;
π
G
MO = 0
3. 4. Eje central y reducción canónica
La ecuación vectorial del eje central y del momento mínimo son respectivamente:
G G
G G
JJJG F × M O
G
MO ⋅ F
OC =
m=
+µF
F
F2
G G
Como puede observarse dependen solo de F y M O . Por otra parte estos valores coinciden con los calculados en el
caso anterior, por ello también coinciden el eje central y la reducción canónica
Ejercicio 2