EXAMEN DE ECONOMETRÍA 20/06/98
Anuncio
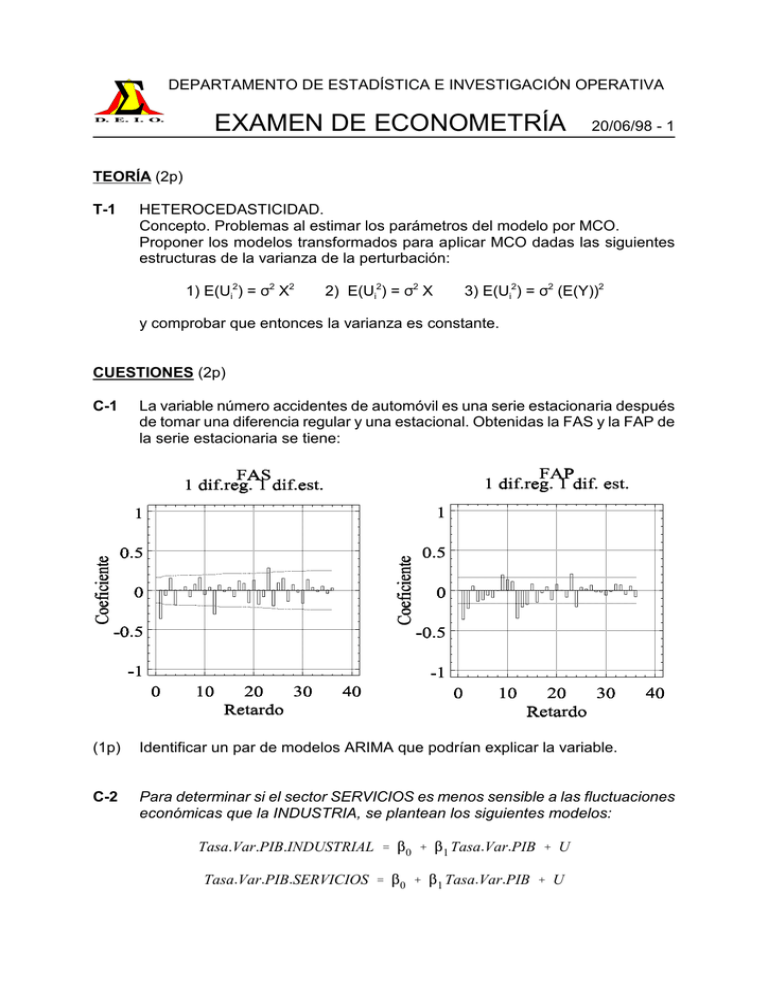
DEPARTAMENTO DE ESTADÍSTICA E INVESTIGACIÓN OPERATIVA EXAMEN DE ECONOMETRÍA 20/06/98 - 1 TEORÍA (2p) T-1 HETEROCEDASTICIDAD. Concepto. Problemas al estimar los parámetros del modelo por MCO. Proponer los modelos transformados para aplicar MCO dadas las siguientes estructuras de la varianza de la perturbación: 1) E(Ui2) = 2 X2 2) E(Ui2) = 2 X 3) E(Ui2) = 2 (E(Y))2 y comprobar que entonces la varianza es constante. CUESTIONES (2p) C-1 La variable número accidentes de automóvil es una serie estacionaria después de tomar una diferencia regular y una estacional. Obtenidas la FAS y la FAP de la serie estacionaria se tiene: (1p) Identificar un par de modelos ARIMA que podrían explicar la variable. C-2 Para determinar si el sector SERVICIOS es menos sensible a las fluctuaciones económicas que la INDUSTRIA, se plantean los siguientes modelos: Tasa.Var.PIB.INDUSTRIAL 0 1 Tasa.Var.PIB U Tasa.Var.PIB.SERVICIOS 0 1 Tasa.Var.PIB U DEPARTAMENTO DE ESTADÍSTICA E INVESTIGACIÓN OPERATIVA EXAMEN DE ECONOMETRÍA 20/06/98 - 2 Ajustando ambos con datos correspondientes al periodo 1971-1990, se obtiene: Model fitting results for: PIB.INDUSTRIAL -------------------------------------------------------------------------------Independent variable coefficient std. error t-value sig.level -------------------------------------------------------------------------------CONSTANT -1.375485 0.564029 -2.4387 0.0253 PIBTOTAL 1.458788 0.141143 10.3355 0.0000 -------------------------------------------------------------------------------R-SQ. (ADJ.) = 0.8478 SE= 1.455279 MAE= 1.111192 DurbWat= 1.893 20 observations fitted, forecast(s) computed for 0 missing val. of dep. var. Model fitting results for: PIB.SERVICIOS -------------------------------------------------------------------------------Independent variable coefficient std. error t-value sig.level -------------------------------------------------------------------------------CONSTANT 1.84478 0.296186 6.2284 0.0000 PIBTOTAL 0.585086 0.074118 7.8940 0.0000 -------------------------------------------------------------------------------R-SQ. (ADJ.) = 0.7634 SE= 0.764204 MAE= 0.567921 DurbWat= 1.841 20 observations fitted, forecast(s) computed for 0 missing val. of dep. var. Para verificar que el sector SERVICIOS es menos sensible a las fases de crisis y expansión de la economía, basta con comprobar que la pendiente del sector INDUSTRIAL toma un valor mayor que uno, y superior a la pendiente del sector SERVICIOS (mas del doble). (1p) ¿Es aceptable ese razonamiento?. Proponer otro modelo que permita responder la pregunta en mejores condiciones. PROBLEMAS (6p) P-1 Se dispone de los valores de la PRODUCCIÓN de GASÓLEO (en miles de toneladas) correspondientes a España, medidos de forma mensual desde el año 1980, e interesa predecir el volumen de dicha producción mediante series temporales. Para ello se ha utilizado la metodología Box-Jenkins, y se ha identificado y estimado un modelo ARIMA. (0.5p) a) ¿Qué ARIMA se ha utilizado y cuál es la expresión del modelo en notación de retardos?. (2.0p) b) Comprobar si se cumple que el residuo es un ruido blanco. (0.5p) c) ¿Qué es lo que falla realmente en el modelo y qué habría que hacer para mejorarlo?. DEPARTAMENTO DE ESTADÍSTICA E INVESTIGACIÓN OPERATIVA EXAMEN DE ECONOMETRÍA 20/06/98 - 3 -------------------------------------------------------------------------------Summary of Fitted Model for: LOG GASOLEO -------------------------------------------------------------------------------Parameter Estimate Stnd.error T-value P-value MA ( 1) 0.73123 0.07138 10.24477 0.00000 MA ( 2) 0.24498 0.07065 3.46755 0.00066 SMA( 12) 0.45473 0.06128 7.42020 0.00000 -------------------------------------------------------------------------------Model fitted to differences of order 1 Model fitted to seasonal differences of order 1 with seasonal length = 12 Estimated white noise variance = 0.0209139 with 182 degrees of freedom. Estimated white noise standard deviation (std err) = 0.144616 Chi-square test statistic on first 20 residual autocorrelations = 21.0041 with probability of a larger value given white noise = 0.226107 Backforecasting: yes Number of iterations performed: 10 -------------------------------------------------------------------------------Residual Summary -------------------------------------------------------------------------------Number of observations = 185 Residual average = 0.00221622 Residual variance = 0.0209139 Residual standard error = 0.144616 Coeff. of skewness = 0.0582091 standardized value = 0.323222 Coeff. of kurtosis = 6.16613 standardized value = 17.1196 DEPARTAMENTO DE ESTADÍSTICA E INVESTIGACIÓN OPERATIVA EXAMEN DE ECONOMETRÍA P-2 20/06/98 - 4 Se va a tratar de utilizar el número de vehículos y motos matriculados en una región española como indicador de su riqueza. Para ello se propone el siguiente modelo: RENTA.PROVINCIAL 0 1 N.AUTOMOVIL 2 N.MOTOS U Se dispone de los valores de la renta provincial (miles de millones de pesetas), del número de automóviles (número de unidades) y del número de motos (número de unidades) de las 50 provincias españolas correspondientes al año 1967. DEPARTAMENTO DE ESTADÍSTICA E INVESTIGACIÓN OPERATIVA EXAMEN DE ECONOMETRÍA 20/06/98 - 5 (0.5p) a) Verificar si son significativos los parámetros del modelo, tanto a nivel individual como conjunto. (0.5p) b) Comprobar si existen problemas de multicolinealidad en el modelo mediante un test adecuado. (0.5p) c) Comprobar si existen problemas de heteroscedasticidad en el modelo mediante un test adecuado. (0.5p) d) Comprobar si existen problemas de autocorrelación en el modelo mediante un test adecuado. (1.0p) e) Formular un modelo que evite los problemas que aparecen. Eigenvalues and Eigenvectors -------------------------------------------------------------------------------Input matrix: MATCORRELACION Eigenvalues = 0.118951 1.88105 INVERSE MATCORRELACION -------------------------------------------------------------------------------4.46921 -3.93759 -3.93759 4.46921 Model fitting results for: RENTA_PROV -------------------------------------------------------------------------------Independent variable coefficient std. error t-value sig.level -------------------------------------------------------------------------------CONSTANT 6343.896542 1127.154621 ; ; AUTOMÓVIL 0.610527 0.024924 ; ; MOTOS 0.110189 0.056593 ; ; -------------------------------------------------------------------------------R-SQ. (ADJ.) = 0.9843 SE= 5417.682157 MAE= 3469.797434 DurbWat= 50 observations fitted, forecast(s) computed for 0 missing val. of dep. var. Analysis of Variance for the Full Regression -------------------------------------------------------------------------------Source Sum of Squares DF Mean Square F-Ratio P-value -------------------------------------------------------------------------------Model ; ; ; ; ; Error ; ; ; ; -------------------------------------------------------------------------------Total (Corr.) 91613543554. 49 R-squared = ; Stnd. error of est. = 5417.68 R-squared (Adj. for d.f.) = 0.984301 Durbin-Watson statistic = 2.29065 Residual Summary -------------------------------------------------------------------------------Number of observations = 50 (0 missing values excluded) Residual average = 9.93168E-12 Residual variance = 2.93513E7 Residual standard error = 5417.68 Coeff. of skewness = 1.14472 standardized value = 3.30451 Coeff. of kurtosis = 6.56895 standardized value = 9.48147 Durbin-Watson statistic = 2.29065 DEPARTAMENTO DE ESTADÍSTICA E INVESTIGACIÓN OPERATIVA EXAMEN DE ECONOMETRÍA Model fitting results for: R01.RESIDUOS1 RAISE 2 -------------------------------------------------------------------------------Independent variable coefficient std. error t-value sig.level -------------------------------------------------------------------------------CONSTANT 2.270048E7 1.650149E7 1.3757 0.1754 AUTOMOVIL 14.916096 364.881304 0.0409 0.9676 MOTOS 172.369886 828.524292 0.2080 0.8361 -------------------------------------------------------------------------------R-SQ. (ADJ.) = 0.0000 SE=79314609.568175 MAE=36098160.531772 DurbWat= 2.201 50 observations fitted, forecast(s) computed for 0 missing val. of dep. var. Flagged Observations for R01.RENTA_PROV ------------------------------------------------------------------Obs. Number Stnd. Residual Leverage Mahalanobis Dist. DFITS 3 -1.37477 0.15413 7.76686 -0.58685 7 -3.37648 0.07428 2.87166 -0.95641 8 0.05350 0.44896 38.1287 0.04829 20 2.34678 0.02023 0.01171 0.33725 28 -0.96076 0.60142 71.4490 -1.18018 46 0.57481 0.20776 11.6084 0.29436 48 5.10535 0.02975 0.49239 0.89404 ------------------------------------------------------------------Number of flagged observations (residual, leverage or DFITS) = 7 20/06/98 - 6