7.- Una empresa de alimentación produce dos tipos de tallarines
Anuncio

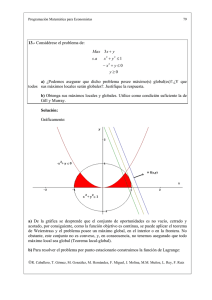
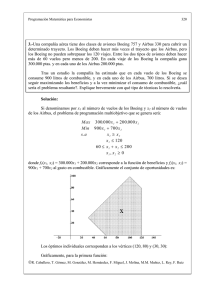
Programación Matemática para Economistas 1 7.- Una empresa de alimentación produce dos tipos de tallarines: delgados y gruesos. Cada kg. de tallarines delgados le reporta a la compañía una ganancia de 2 u.m. y requiere 6 minutos en su máquina cortadora. Cada kg. de tallarines gruesos produce una ganancia neta de 1,4 u.m. y precisa 4 minutos de tiempo en la máquina. La empresa tiene 40 horas de tiempo máquina disponible esta semana y necesita producir, al menos, 100 kg. de tallarines delgados y 250 kg. de tallarines gruesos. Además de maximizar la ganancia total, la empresa quiere minimizar el consumo de energía. Se sabe que el consumo de energía es de 1 kw. por kg. de tallarín delgado y la misma cantidad por kg. de tallarín grueso. a) Formule el problema de programación multiobjetivo que permita obtener el plan de producción que maximiza las ganancias de la empresa y minimiza el consumo de energía. b) Si la máxima ganancia se alcanza en el punto (100, 450) y, por otra parte, el mínimo de consumo de energía en (100, 250), elabore la matriz de pagos. c) Si es posible, dibuje el conjunto de puntos eficientes. d) ¿Qué se entiende por solución satisfactoria? Indique alguna técnica para su obtención. Solución: a) Denotemos por x1 al número de kg. de tallarines delgados y por x2 a los kg. de tallarines gruesos. Las restricciones del problema se corresponden, en primer lugar, con el tiempo disponible en la máquina cortadora y, en segundo lugar, con las necesidades de producción. Así, las restricciones del problema serían las siguientes: 6x1 + 4x2 ≤ 2400 x1 ≥ 100 x2 ≥ 250 x1 , x2 ≥ 0 El conjunto de oportunidades es: ©R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz Programación Matemática para Economistas 2 Los objetivos de la empresa son, por un lado, maximizar las ganancias de la empresa y, por otro, minimizar el consumo de energía. Así pues, los objetivos son: Max 2x1 + 1,4x2 Min x1 + x2 Por tanto, el problema multiobjetivo que permite el plan de producción que maximiza las ganancias de la empresa y minimiza el consumo de energía es el siguiente: Max 2x1 + 1,4x2 Min x1 + x2 s. a 6x1 + 4x2 ≤ 2400 x1 ≥ 100 x2 ≥ 250 x1 , x2 ≥ 0 Para la obtención de los óptimos individuales, tendríamos que resolver dos problemas correspondientes a: ©R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz Programación Matemática para Economistas 3 1. Beneficios Max B(x1, x2 ) = 2x1 + 1,4x2 s. a 6x1 + 4x2 ≤ 2400 x1 ≥ 100 x2 ≥ 250 x1 , x2 ≥ 0 2. Energía Min E(x1, x2 ) = x1 + x2 s. a 6x1 + 4x2 ≤ 2400 x1 ≥ 100 x2 ≥ 250 x1 , x2 ≥ 0 Si representamos gráficamente ambos problemas, calculando sus correspondiente óptimos y curvas de nivel, obtenemos que: f1(x1, x2) = B(x1, x2) alcanza su máximo en el vértice (100, 450) f2(x1, x2) = E(x1, x2) alcanza su mínimo en el vértice (100, 250) ©R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz Programación Matemática para Economistas 4 b) La matriz de pagos, tras evaluar los óptimos individuales en el otro objetivo, nos quedaría: * 1 * 2 x = (100, 450) x = (100, 250) f1 = B 830 550 -f2 = -E -550 -350 Hemos considerado -f2 para tener los dos objetivos bajo máximo. c) En el apartado anterior ya hemos representado gráficamente el conjunto de oportunidades y obtenido los óptimos individuales. El conjunto de puntos eficientes se corresponde con el segmento de la frontera del conjunto de oportunidades que va desde el punto (100, 250) al punto (233.33, 250) y el segmento que va de este último al punto (100,450). ©R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz Programación Matemática para Economistas 5 d) Una solución satisfactoria es un punto que verifica las restricciones originales del problema y además las metas impuestas por el decisor, en el caso de que éste haya impuesto niveles de aspiración a los objetivos del problema. La técnica que encuentra soluciones satisfactorias se conoce como Programación por Metas. ©R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz