1.1 Distancia entre dos puntos
Anuncio

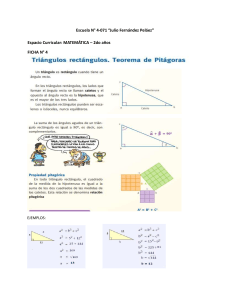
La línea recta. La recta se define como el lugar geométrico de todos los puntos de un plano que al tomarse de dos en dos se obtiene la misma pendiente. Distancia entre dos puntos. Sea el punto A(x1, y1) y el punto B(x2, y2) dos puntos en un plano cartesiano como el que se muestra en la siguiente figura. Al trazar líneas paralelas a los ejes que pasen por cada uno de los puntos se forma un triángulo rectángulo en donde la hipotenusa “d” es la distancia entre A y B y los catetos son los segmentos AP y BP , entonces si aplicamos el teorema de Pitágoras se tiene que: B y2 2 2 2 d = ( AP ) + ( BP ) AP = x2- x1 y BP = y2 - y1 Pero d 2 2 2 Por lo tanto d = (x2- x1 ) + (y2 - y1) y1 A 1 1y1 P 1 x1 d = (x 2 − x 1 ) 2 + (y 2 − y1 ) 2 x2 Ejemplo 1. Obtener la distancia entre los puntos A(1, -2 ) y B(4, 3). d = (x 2 − x1 ) 2 + (y 2 − y1 ) 2 d= (4 − 1)2 + (3 − (− 2))2 (3)2 + (3 + 2)2 2 9 + (5) 9 + (25) d= 34 d= d= d= d= 5.83 Ejemplo 2. Dados los puntos A(0, 4), B(-2, 0) y C(2, 0) demostrar que los puntos forman un triángulo isósceles. Debemos recordar que en triángulo isósceles la medida de dos de sus lados son iguales y uno diferente. Deberemos determinar la medida de sus tres lados. d AB = (x 2 − x 1 ) 2 + (y 2 − y1 ) 2 d AB = (− 2 − 0 )2 + (0 − 4)2 (− 2 )2 + (− 4 )2 d AB = 4 + 16 d AB = = 20 d AB = 4.47 d AB d AC = (x 2 − x 1 ) 2 + (y 2 − y1 ) 2 d BC = (x 2 − x 1 ) 2 + (y 2 − y1 ) 2 d AC = (2 − 0)2 + (0 − 4 )2 d BC = (2 − (−2) )2 + (0 − 0)2 d AC = (2)2 + (− 4)2 d BC = (2 + 2 )2 + (0 )2 d AC = 4 + 16 d BC = (4 )2 + (0 )2 d AC = 20 d BC = 16 d AC = 4.47 d BC = 4 Como la distancia d AC = d AB y éstas son diferentes a triángulo isósceles. d BC , entonces se trata de un