programa geometría analítica

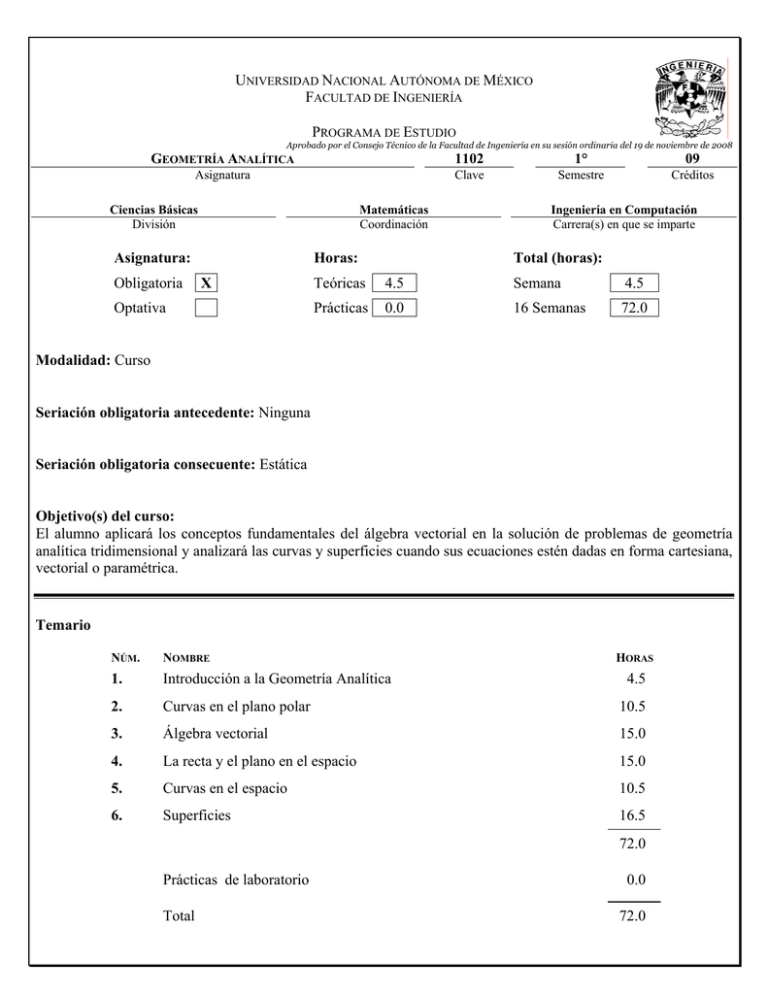
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO
FACULTAD DE INGENIERÍA
PROGRAMA DE ESTUDIO
Aprobado por el Consejo Técnico de la Facultad de Ingeniería en su sesión ordinaria del 19 de noviembre de 2008
GEOMETRÍA ANALÍTICA
1102
1°
09
Asignatura
Clave
Semestre
Créditos
Ciencias Básicas
División
Matemáticas
Coordinación
Asignatura:
Obligatoria
Horas:
X
Optativa
Ingeniería en Computación
Carrera(s) en que se imparte
Total (horas):
Teóricas
4.5
Semana
4.5
Prácticas
0.0
16 Semanas
72.0
Modalidad: Curso
Seriación obligatoria antecedente: Ninguna
Seriación obligatoria consecuente: Estática
Objetivo(s) del curso:
El alumno aplicará los conceptos fundamentales del álgebra vectorial en la solución de problemas de geometría
analítica tridimensional y analizará las curvas y superficies cuando sus ecuaciones estén dadas en forma cartesiana,
vectorial o paramétrica.
Temario
NÚM.
NOMBRE
HORAS
1.
Introducción a la Geometría Analítica
2.
Curvas en el plano polar
10.5
3.
Álgebra vectorial
15.0
4.
La recta y el plano en el espacio
15.0
5.
Curvas en el espacio
10.5
6.
Superficies
16.5
4.5
72.0
Prácticas de laboratorio
Total
0.0
72.0
GEOMETRÍA ANALÍTICA
(2 / 5)
1 Introducción a la Geometría Analítica
Objetivo: El alumno identificará los antecedentes históricos y principios de la geometría analítica:
Geometría Euclidiana y geometrías no Euclidianas.
Contenido:
1.1 Breve reseña histórica: Geometría Euclidiana y geometrías no Euclidianas.
1.2 Introducción al sistema de coordenadas cartesianas en el plano y en el espacio de tres dimensiones.
2 Curvas en el plano polar
Objetivo: El alumno obtendrá ecuaciones en forma polar de curvas en el plano y determinará las
características de éstas a partir de su ecuación en forma polar.
Contenido:
2.1 Sistema de coordenadas polares. Simetría de puntos en coordenadas polares.
2.2 Transformación de coordenadas cartesianas a polares y de polares a cartesianas.
2.3 Ecuaciones polares de curvas. Cardioides, lemniscatas, rosas de n pétalos.
2.4 Análisis de una curva representada por una ecuación polar.
3 Álgebra vectorial
Objetivo: El alumno aplicará el álgebra vectorial en la resolución de problemas geométricos.
Contenido:
3.1 Sistema cartesiano en tres dimensiones. Simetría de puntos.
3.2 Cantidades escalares y cantidades vectoriales. Definición de segmento dirigido. Componentes
escalares de un segmento dirigido en la dirección de los ejes coordenados. El vector como terna
ordenada de números reales. Definición de módulo de un vector e interpretación geométrica. Vector
de posición de un punto. Vector nulo. Vector unitario. Vectores unitarios i, j, k. Vectores
representados por una combinación lineal de los vectores i, j, k.
3.3 Definición de igualdad de vectores. Operaciones con vectores: adición, sustracción y multiplicación
por un escalar. Propiedades de las operaciones.
3.4 Producto escalar de dos vectores y propiedades. Condición de perpendicularidad entre vectores.
Componente escalar y componente vectorial de un vector en la dirección de otro. Ángulo entre dos
vectores. Ángulos, cosenos y números directores de un vector.
3.5 Producto vectorial: definición, interpretación geométrica y propiedades. Condición de paralelismo
entre vectores. Aplicación del producto vectorial al cálculo del área de un paralelogramo.
3.6 Producto mixto e interpretación geométrica.
GEOMETRÍA ANALÍTICA
(3 / 5)
4 La recta y el plano en el espacio
Objetivo: El alumno aplicará el álgebra vectorial para obtener las diferentes ecuaciones de la recta y del
plano, así como para determinar las relaciones entre ellos y con puntos en el espacio de tres dimensiones.
Contenido:
4.1 Ecuación vectorial y ecuaciones paramétricas de la recta. Ecuaciones cartesianas en forma simétrica
y en forma general de la recta.
4.2 Distancia de un punto a una recta. Ángulo entre dos rectas. Condición de perpendicularidad y
condición de paralelismo entre rectas. Distancia entre dos rectas. Intersección entre dos rectas.
4.3 Ecuación vectorial, ecuaciones paramétricas y ecuación cartesiana del plano. Distancia de un punto
a un plano. Ángulo entre dos planos. Condición de perpendicularidad y condición de paralelismo
entre planos. Distancia entre dos planos. Intersección entre planos.
4.4 Relaciones entre rectas y planos: ángulo entre una recta y un plano, condición de paralelismo y
condición de perpendicularidad. Intersección de una recta con un plano. Distancia entre una recta y
un plano.
5 Curvas en el espacio
Objetivo: El alumno obtendrá ecuaciones paramétricas y en forma vectorial de curvas en el espacio e
identificará curvas a partir de sus ecuaciones.
Contenido:
5.1 Ecuaciones paramétricas y ecuación vectorial de una curva contenida en planos paralelos a los
planos coordenados. Intervalo paramétrico.
5.2 Ecuaciones paramétricas y ecuación vectorial de las cónicas.
5.3 Ecuaciones cartesianas de una curva plana en el espacio, obtenidas a partir de sus ecuaciones
paramétricas.
6 Superficies
Objetivo: El alumno identificará superficies cuádricas a partir de su ecuación cartesiana; y obtendrá la
ecuación vectorial, las ecuaciones paramétricas y la ecuación cartesiana de superficies.
Contenido:
6.1 Clasificación de superficies. Superficies cuádricas. Definición de superficies cilíndricas, cónicas,
regladas y de revolución.
6.2 Ecuación vectorial y ecuaciones paramétricas de una superficie cuádrica.
6.3 Obtención de la ecuación cartesiana por el método de las generatrices.
6.4 Ecuación cartesiana de una superficie a partir de una de sus ecuaciones vectoriales.
6.5 Determinación de las características de una superficie cuádrica (identificación) a partir de su
ecuación cartesiana.
(4 / 5)
GEOMETRÍA ANALÍTICA
Bibliografía básica:
BELL, E. T.
Historia de las Matemáticas
2a edición
México
Fondo de Cultura Económica, 1995
Temas para los que se recomienda:
1
CASTAÑEDA De I. P., Érik
Geometría analítica en el espacio
México
Facultad de Ingeniería - UNAM, 2003
2, 3, 4, 5 y 6
SOLÍS U., Rodolfo et al.
Geometría analítica
México
Limusa-Facultad de Ingeniería, UNAM, 1999
3, 4, 5 y 6
SWOKOWSKI, Earl
Cálculo con geometría analítica
11a edición
México
Cengage Learning, 2007
Todos
Bibliografía complementaria:
RUIZ ZÚÑIGA, ÁNGEL
Geometrías no euclidianas
Breve historia de una gran revolución intelectual
1a edición
Editorial de la Universidad de Costa Rica, 1999
1
LEHMANN, Charles
Geometría analítica
México
Limusa, 2008
2, 3, 4, 5 y 6
MENNA G., Zózimo
Geometría analítica del espacio un Enfoque Vectorial
México
Limusa, 1981
3y6
(5 / 5)
GEOMETRÍA ANALÍTICA
RIDDLE DOUGLAS F.
Analytic geometry
6th edition
Boston
PWS Publishing Company, 1996
Sugerencias didácticas:
Exposición oral
Exposición audiovisual
Ejercicios dentro de clase
Ejercicios fuera del aula
Seminarios
Forma de evaluar:
Exámenes parciales
Exámenes finales
Trabajos y tareas fuera del aula
2, 3, 4, 5 y 6
X
X
X
X
X
X
X
Lecturas obligatorias
Trabajos de investigación
Prácticas de taller o laboratorio
Prácticas de campo
Otras: Empleo de nuevas
tecnologías
X
X
Participación en clase
Asistencias a prácticas
Otras
X
X
Perfil profesiográfico de quienes pueden impartir la asignatura
Licenciatura en Ingeniería, Matemáticas, Física o carreras cuyo contenido en el área de matemáticas sea similar.
Deseable haber realizado estudios de posgrado, contar con experiencia docente o haber participado en cursos o
seminarios de iniciación en la práctica docente.