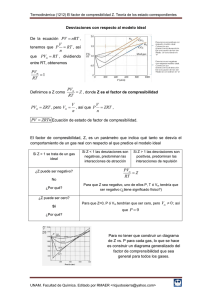
= TRZn Vp = usar la función pseudo-presión de un gas real: ( ) λ λ
Anuncio

SIMULACION NUMERICA DE RESERVORIOS Práctica 1 1- De la ecuación general del flujo monofásico en un medio poroso y especificando todas las hipótesis que aplica, deducir las ecuaciones que rigen el movimiento de: a) Flujo monofásico lineal, 1-D, horizontal, de un fluido incompresible (agua) de viscosidad constante. Suponer además que la compresibilidad de la formación es despreciable y que el medio poroso es homogéneo. b) Flujo monofásico radial, 1-D, horizontal, de un fluido de compresibilidad constante y pequeña (petróleo) y viscosidad constante. Suponer además que la compresibilidad de la formación es despreciable, que el medio poroso es homogéneo y que no existen términos fuente o sumidero. c) Flujo monofásico radial, 1-D, horizontal, de un gas ideal. Suponer además que la compresibilidad de la formación es despreciable, que el medio poroso es homogéneo y que no existen términos fuente o sumidero.(Sugerencia: usar la ecuación de estado de los gases ideales p V = n R T y considerar que la viscosidad de un gas ideal es constante en un medio isotérmico). d) Flujo monofásico lineal, 1-D, horizontal, de un gas real. Suponer además que la compresibilidad de la formación es despreciable, que el medio poroso es homogéneo y que no existen términos fuente o sumidero. . (Sugerencia: usar la ecuación de estado de los gases reales p V = Zn R T y usar la función pseudo-presión de un gas real: m( p ) = p 2λ ∫ µ(λ ) Z (λ )dλ ) p0 2. De las siguientes pw , po , Sw , So ecuaciones, cuya formulación tiene como incógnitas kk q ∂ S ∇. rw ( ∇pw − ρw g ∇D) + w = φ w µw Bw ρw ∂ t Bw kk q ∂ S ∇. ro ( ∇po − ρo g ∇D) + o = φ o µo Bo ρo ∂ t Bo pc = po − pw Sw + So = 1 deducir nuevas formulaciones, en las que las derivadas espaciales y temporales queden únicamente en función de: a) pw y po b) po y pc c) po y Sw 3. Deducir la ecuación en saturación (ecuación de Buckley-Leverett): α(S) ∂S ∂S = ∂x ∂t que describe el flujo de dos fases (agua-petróleo) en arena, bajo las siguientes condiciones: flujo unidimensional, horizontal, fluidos incompresibles, fuerzas capilares despreciables y sin fuentes ni sumideros. 1 de 3 SIMULACION NUMERICA DE RESERVORIOS Práctica 1 4 - Soluciones analíticas-gráficas de Buckley-Leverett (Método de Welge) a) Se decide realizar una inundación con agua en un reservorio con las siguientes propiedades de la roca y los fluidos: Swc = 0.2 µw =1 cp Bw = 1 Sor = 0.2 µo = 1 cp Bo = 1.28 α = 0º Sw krw kro 0.20 0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60 0.65 0.70 0.75 0.80 0 0.002 0.009 0.020 0.033 0.051 0.075 0.100 0.132 0.170 0.208 0.251 0.300 0.800 0.670 0.555 0.445 0.354 0.273 0.199 0.136 0.087 0.052 0.020 0.006 0 Se desea determinar : i) La saturación de agua en el frente y la saturación de agua por detrás de él. ii) La eficiencia al desplazamiento al tiempo de breakthrough. iii) El porcentaje de agua en la producción. b) Se desea analizar el mecanismo de inundación con agua en un reservorio que tiene las siguientes propiedades: k rw = * k rw S w − S wc ∗ 1 − S wc − S or k ro = * k ro 1 − S w − S or ∗ 1 − S wc − S or nw no krw* = 0.2 kro* = 0.8 nw = 2 no = 2 Swc = 0.25 Sor = 0.2 2 de 3 SIMULACION NUMERICA DE RESERVORIOS Práctica 1 i) Determinar el flujo fraccional al tiempo de breakthrough en los tres casos siguientes: Caso 1 2 3 µo (cp) 50 5 0.5 µw (cp) 0.4 1 1 ii) Comparar los resultados y sacar conclusiones. 5. De las ecuaciones del modelo composicional, y especificando todas las hipótesis que aplica, deducir las ecuaciones que rigen el movimiento de: a) flujo monofásico bidimensional en coordenadas cilíndricas (r,z), de un fluido de compresibilidad c constante y pequeña (petróleo) y viscosidad constante. Suponer además que la compresibilidad de la formación es despreciable, que el medio poroso es homogéneo y que no existen términos fuente o sumidero. b) flujo trifásico, sin transferencia de masa, bidimensional en coordenadas cilíndricas (r,z). Suponer que las fases agua y petróleo son incompresibles y la fase gas es compresible. Considerar además que la compresibilidad de la formación es despreciable y que el medio poroso es homogéneo 6. De las ecuaciones del modelo black-oil, y especificando todas las hipótesis que aplica, deducir las ecuaciones que rigen el movimiento de: a)- Flujo monofásico bidimensional en coordenadas cartesianas x, y, horizontal, de un fluido de compresibilidad constante y pequeña (petróleo) y viscosidad constante. Suponer además que la compresibilidad de la formación es despreciable y que el medio poroso es isótropo y homogéneo. b)- Flujo bifásico incompresible (agua-petróleo) bidimensional en coordenadas cartesianas x, y ; horizontal, de fluidos de viscosidad constante. Suponer además que la compresibilidad de la formación es despreciable y que el medio poroso es isótropo y homogéneo. 7. Deducir el modelo que representa un flujo trifásico (g-o-w) de tres componentes (G-O-W) y que considera la solubilidad de la componente gas (G) en las fases oleosa y acuosa (o-w) y la vaporización de la componente petróleo (O) en la fase gaseosa (g). Para ello utilizar : V V Rso = GS Rsw = GS y VOS VWS V Rv = OS (volatilidad del petróleo en el gas) VGS 3 de 3