Cálculo Diferencial e Integral II - Repositorio CB
Anuncio

COLEGIO DE BACHILLERES
SECRETARÍA ACADÉMICA
COORDINACIÓN DE ADMINISTRACIÓN
ESCOLAR Y DEL SISTEMA ABIERTO
COMPENDIO FASCICULAR
CÁLCULO DIFERENCIAL
E INTEGRAL II
p
FASCÍCULO 1.
LA INTEGRAL DEFINIDA
FASCÍCULO 2.
LA INTEGRAL INDEFINIDA
DIRECTORIO
Roberto Castañón Romo
Director General
Luis Miguel Samperio Sánchez
Secretario Académico
Héctor Robledo Galván
Coordinador de Administración
Escolar y del Sistema Abierto
Derechos reservados conforme a la Ley
© 2004, COLEGIO DE BACHILLERES
Prolongación Rancho Vista Hermosa núm. 105
Col. Ex Hacienda Coapa
Delegación Coyoacán, CP 04920, México, D.F.
ISBN 970 632 262-0
PRESENTACIÓN GENERAL
El Colegio de Bachilleres en respuesta a la inquietud de los estudiantes de contar con
materiales impresos que faciliten y promuevan el aprendizaje de los diversos campos del
saber, ofrece a través del Sistema de Enseñanza Abierta y a Distancia este compendio
fascicular, resultado de la participación activa, responsable y comprometida del personal
académico, que a partir del análisis conceptual, didáctico y editorial aportaron valiosas
sugerencias para su enriquecimiento, y aunarse a la propuesta educativa de la
Institución.
Este compendio fascicular es producto de un primer esfuerzo académico del Colegio por
ofrecer a todos sus estudiantes un material de calidad que apoye su proceso de
enseñanza-aprendizaje, conformado por fascículos
Por lo tanto, se invita a la comunidad educativa del Sistema de Enseñanza Abierta y a
Distancia a compartir este esfuerzo y utilizar el presente material para mejorar su
desempeño académico.
DIRECCION GENERAL
P RE S E N T AC I Ó N D E L CO M P E N DI O F AS C I C UL A R
Estudiante del Colegio de Bachilleres, te presentamos este compendio fascicular que
servirá de base en el estudio de la asignatura “Cálculo Diferencial e Integral II” y
funcionará como guía en tu proceso de Enseñanza – Aprendizaje.
Este compendio fascicular tiene la característica particular de presentarte la información
de manera accesible, propiciando nuevos conocimientos, habilidades y actitudes que te
permitirán el acceso a la actividad académica, laboral y social.
Cuenta con una presentación editorial integrada por fascículos, capítulos y temas que te
permitirán avanzar ágilmente en el estudio y te llevarán de manera gradual a consolidar
tu aprendizaje de esta asignatura. Lo anterior tiene como finalidad que puedas
comprender el concepto fundamental del Cálculo Integral así como sus nociones
básicas, es decir, que a partir del planteamiento de problemas en los que sea necesario
calcular el área bajo la curva de la función, puedas obtener el modelo del problema y
aplicar los métodos de integración para la solución de los mismos. Para lograr lo
anterior, este material se apoya en la representación de gráficas de funciones y
utilización de métodos matemáticos para cuantificar, describir y pronosticar los cambios.
COLEGIO DE BACHILLERES
CÁLCULO DIFERENCIAL
E INTEGRAL II
FASCÍCULO 1. LA INTEGRAL DEFINIDA
UNA VISIÓN ESTÁTICA
Autores: Guadalupe Xóchitl Chávez Pérez
Sergio Sánchez Carrillo
1
2
Í N D I C E
INTRODUCCIÓN
5
PROPÓSITO
9
CAPÍTULO 1. INTEGRAL DEFINIDA
11
1.1 ÁREA BAJO LA GRÁFICA DE UNA RECTA
13
1.2 ÁREA BAJO LA GRÁFICA DE UNA CURVA
22
1.3 INTEGRAL DEFINIDA
37
1.4 PROPIEDADES DE LA INTEGRAL DEFINIDA
41
1.5 TEOREMA FUNDAMENTAL DEL CÁLCULO
44
RECAPITULACIÓN
48
ACTIVIDADES DE CONSOLIDACIÓN
49
AUTOEVALUACIÓN
51
ACTIVIDADES DE GENERALIZACIÓN
53
BIBLIOGRAFÍA CONSULTADA
54
3
4
INTRODUCCIÓN
Desde épocas remotas el hombre se enfrentó al problema de la cantidad y la medida,
sobre todo de medir longitudes, áreas y volúmenes. Cuando estas longitudes eran
segmentos de rectas o una sucesión finita de dichos segmentos, el problema de medir
su longitud no representaba gran dificultad.
Figura 1.
Análogamente, cuando se quería medir áreas de polígonos, aunque fueran irregulares, el
problema se resolvía dividiendo el polígono irregular en triángulos –esto demuestra que
siempre lo podemos hacer, y calculada el área de cada triángulo, se decía que el
problema estaba resuelto, ya que la suma de las áreas de dichos triángulos es el área
buscada del polígono irregular.
Figura 2.
5
De la misma manera, nuestros antepasados podían calcular con extraordinaria exactitud
el volumen de cuerpos cuyas fronteras (caras) fueran superficies planas (polígonos),
como paralelepípedos, pirámides, etcétera.
Figura 3.
Estos conocimientos se aplicaron de manera excepcional en la construcción de grandes
obras que hoy nos sorprenden. Pero no solamente en la construcción se tiene dicho
conocimiento sino también en muchas otras ramas del saber humano, como el
conocimiento del movimiento de los astros.
Sin embargo, calcular la longitud de una línea cuando ésta es curva, o encontrar el área
de una región determinada por una curva cerrada o encontrar el volumen de un cuerpo
cuya superficie ya no es plana sino curva, constituyó un verdadero reto en la antigüedad.
Hoy en la actualidad, con el estudio del Cálculo Integral, ya no es gran problema, puesto
que con su aplicación, tenemos la posibilidad de calcular el área de figuras irregulares
como las siguientes:
Figura 4.
El método para encontrar el área de estas figuras se conoce como método de exahución.
Un problema famoso característico que ilustra la obtención del área en figuras irregulares
es el de encontrar el área del círculo, esto es, aproximarnos al área del círculo por medio
de una red de cuadrados cada vez más fina. Esto se consideró imposible, pues por muy
fina que fuera la red siempre tendrían el problema del elemento.
6
Figura 5.
¿Qué significa que un círculo mida x metros cuadrados de área?, ¿Significa que
podemos cubrir con x metros cuadrados la superficie del círculo? Para responder
resuelve el siguiente ejemplo:
2
Dibuja un círculo con un radio (r) de 20 cm. y calcula su área mediante la fórmula A = r .
Ahora dibuja un cuadrado de 35.449 cm. de lado y recórtalo. ¿Cuál es el área de este
cuadrado?
Después de recortar el cuadrado en partes iguales e irlas acomodando dentro del
círculo, hasta llenarlo completamente, ¿qué sucede?
Al principio podrás acomodar partes del cuadrado relativamente grandes, pero conforme
avances observarás que tienes que ir cortando partes cada vez más pequeñas hasta
quedar algunos huecos por llenar y pedazos del cuadrado por acomodar. ¿Qué pasa
entonces? ¿Tienen o no el círculo y el cuadrado aproximadamente la misma área?
¿Tenían o no razón en la antigüedad respecto a la conclusión que llegaron? Este tipo de
problemas y otros podrás resolver por medio del estudio de este fascículo.
Definir el área para figuras geométricas en general, implica un proceso de límite, es por
ello que a lo largo del contenido del fascículo obtendrás aproximaciones de los
resultados de problemas que impliquen sumas infinitas, calcularás el área exacta bajo
una curva para establecer la Integral Definida y concluirás con el Teorema Fundamental
de Cálculo.
7
8
P R O P Ó S I T O
El problema básico de la derivación es: dado
el recorrido de un punto móvil, calcular su
velocidad, o bien, dada una curva, calcular su
pendiente. El problema básico de la integración es
el inverso: dada la velocidad de un punto móvil en
cada instante, hallar su trayectoria, o bien, dada la
pendiente de una curva en cada uno de sus
puntos, calcular la curva.
Hans Hahn (1897-1934)
El contenido de este fascículo pretende que al finalizar su estudio:
¿QUÉ APRENDERÁS?
A obtener el área bajo la gráfica de una
función f(x) en un intervalo de valores a,b,
estimar áreas por métodos numéricos, el
concepto
de
integral
definida,
sus
propiedades y relación con la derivada,
además del Teorema Fundamental del
Cálculo.
¿CÓMO LO APRENDERÁS?
Por medio del desarrollo y solución de
problemas en los que se requiera conocer el
resultado acumulado de procesos de cambio
y situaciones problemáticas en rectángulos.
¿PARA QUÉ TE VA A SERVIR?
Para resolver problemas cuya solución esté
dada por el cálculo de integrales definidas.
9
10
CAPÍTULO 1
INTEGRAL DEFINIDA
Entre los precursores del Cálculo Integral está Arquímedes (287–212 a. C.), quien logró
calcular el área de la superficie de un segmento parabólico mediante integraciones y
descomponiendo una superficie plana en fajas rectangulares sumamente estrechas.
Képler, quien descubrió la ley de las áreas con base en integraciones, también concibió
a los sólidos como formados por un número sumamente grande de elementos
infinitesimales, ya sean triángulos, rectángulos, discos o conos. Buenaventura Cavalieri
(1598–1647), en su Geometría de los Indivisibles calculó la longitud de líneas, áreas de
volúmenes, recurriendo a sumas; John Wallis (1616–1703) estableció cuadraturas y
curvaturas con base en los descubrimientos de Cavalieri.
Puesto que el concepto de integral se deriva de la suma, en un principio se le concibió
como la suma de una infinidad de rectángulos con una dimensión infinitesimal. Después
de que Barro (1669) descubrió que el problema de calcular el área con arreglo a curva es
el inverso del cálculo de la pendiente de la tangente y que Newton y Leibniz
reconocieron, a su vez, que la integración y la diferenciación son procesos inversos, se
definió la integral de una función de cierta variable independiente por la diferencial de
esta variable, como otra función cuya derivada era la función propuesta.
Los trabajos de Newton relativos al cálculo son anteriores a los de Leibniz, pero el
primero nada publicó en un principio, limitándose a exponer en sus cátedras los
descubrimientos que había hecho; no así Leibniz, quien publicó una notación distinta a
las de Newton, el cual basó su concepción en la noción de velocidad de partículas,
considerando lo que él llamó crecimiento instantáneo, mientras que Leibniz partió del
concepto de diferencias sumamente pequeñas.
11
El método de las fluxiones, que concibió Newton a los 20 años y redactó a los 23, se dio
a conocer después de su muerte; pero insertó una breve nota que da a conocer este
método en sus memorias, Philosophia Naturalis Principia Matemática, en donde utiliza
este método, aplicado no sólo a problemas de Matemática pura, sino a fenómenos
celestes.
Leibniz, durante su primera estancia en París (1692), creó los procedimientos
infinitesimales de indiscutible originalidad y admirable potencia, en que destaca la
tendencia simbolizadora. Estudió el problema de las tangentes y su inverso.
Respecto a la tangente y su inversa, Leibniz introdujo el nuevo signo de la integral,
representando con y la misma cantidad que Cavalieri consideraba como suma de
ordenadas y designaba por omn (omnia, o sea, la suma de todas las y).
Al ver como en la operación indicada por el signo
se eleva el grado, infirió que la
x
, que
d
luego abandonó para adoptar dx, de cuyo significado sólo dio Leibniz esta explicación:
diferencia entre dos x próximas. Son suyas las notaciones dx, dy/dx, lo mismo que la
palabra derivada.
operación lo rebaja, y como esto suele suceder en la división, creó la notación
Numerosos matemáticos completaron la obra iniciada por Newton y Leibniz. Deben
citarse, entre ellos, a Jacobo Bernoulli (1654-1705), quien escribió una carta a Leibniz en
1687 para solicitarle esclareciera la comprensión del nuevo cálculo; pero como Leibniz
estaba de viaje, la carta le llegó hasta 1690. La tardanza de la respuesta causó que
Jacobo Bernoulli se dedicase a la tarea de penetrar los secretos del Cálculo Diferencial,
tanto él como su hermano Juan (1667-1748) dieron muestras de aptitudes excepcionales
para la investigación matemática, por lo que Leibniz declaró que ésta era tanto de ellos
como suya.
El barón Agustín Luis Cauchy (1789-1857) fue el primero en demostrar, de manera
rigurosa y plenamente satisfactoria y con base en el método de los límites, la
consistencia de sus principios fundamentales.
A Jacobo Bernoulli se debe la denominación de Cálculo Integral, sugerida en 1690 y
adoptada por Leibniz en 1696. La integración por sustitución fue aplicada por Jacobo
Bernolli desde los primeros tiempos del cálculo y la expresión cambio de variable se
encuentra en las obras de Cauchy. La integración por partes, consecuencia inmediata de
la fórmula de la diferencial de un producto, se encuentra accidentalmente en Brook
Taylor, pero la denominación se debe a Silvestre F. Lacroix (1765-1843).
La notación
b
a
es de José Fourier (1768-1830) y se publicó por primera vez en la
Théorie analytique de la Chaleur, de 1822, innovación que se adoptó de inmediato y dio
a la expresión de la integral definida, la cual está representa como,
12
b
a F( x) dx .
1.1 ÁREA BAJO LA GRÁFICA DE UNA RECTA
A continuación te presentamos el cálculo del área bajo distintas funciones constantes,
para que observes que la integral es la operación inversa de la derivada.
Para contestar las preguntas que se formularon en la introducción, primero calcularemos
áreas de rectángulos. Supongamos que tenemos la función constante ƒ(x) = 1.
Figura 6.
Primero se calcula el área comprendida bajo esta función; entre las rectas x = 0, x = 1 y
2
el eje X, se sabe que el área de un cuadrado es l , y como el lado mide 1, entonces el
área es 1.
Figura 7.
Ahora calculemos el área comprendida bajo la misma función; las rectas x = 0,x = 2 y el
eje X.
13
Figura 8.
Vemos en la figura 8 que se trata de un rectángulo, por lo tanto, el área es 2.
Con los mismos datos, sólo variando la recta cuya ecuación al principio fue x = 1 y luego
x = 2, ahora por x = 3, tenemos que el área del nuevo rectángulo es 3 y así
sucesivamente.
Figura 9.
El valor de la base de los rectángulos la denotaremos como x.
Completa la tabla 1.
Tabla 1.
14
Se advierte que el cálculo del área nos lleva a obtener una nueva función A 1(x); el valor
del área A1(x) depende de x. La gráfica de la nueva función queda como sigue:
Figura 10.
Esta función es continua ya que sólo calculamos el valor del área para valores de x
enteros positivos, pero también se puede calcular el valor para x en todos los reales
1
1
positivos; por ejemplo, si x , entonces el área es .
2
2
¿Cómo se llama la nueva función?
Ahora podemos pensar en calcular el área bajo la función identidad (anterior), la recta x
= 1 y el eje X.
Figura 11.
Como se trata de un triángulo rectángulo, el área se obtiene mediante la fórmula
base x altura
1
, mas como la base y la altura valen 1, entonces el área es .
2
2
15
Al calcular el área bajo la función identidad, la recta x = 2 y eje X, análogamente nos
queda un triángulo rectángulo cuya base y altura valen 2.
Figura 12.
Por consiguiente, el área es 2. para comprenderlo mejor observa la tabla 2.
Tabla 2,
x
ƒ(x)
A1(x)
1
1
1
2
1
2
3
1
3
4
1
4
5
1
5
6
1
6
7
1
7
8
1
8
9
1
9
10
1
10
16
A2(x)
1
2
4
2
9
2
16
2
25
2
36
2
49
2
64
2
81
2
100
2
La primera columna de la tabla 2 es el valor de x; la segunda son valores de la función
constante, en este caso 1; la tercera es el valor de las áreas de la función constante
conforme cambia el valor de x que da como resultado otra función llamada identidad, y la
cuarta columna son los valores del área delimitada por la función identidad, el eje X y las
rectas que van variando x = 1, x = 2,..., x = 10.
¿Qué se observa en los resultados de la última columna de la tabla 2?
¿Cuál es el área de la región comprendida debajo de la función identidad, el eje X y la
recta x = n cuando n es número real positivo?
Es
n2
.
2
x2
, lo que
2
nos conduce a otra función que es la mitad de la función cuadrática (figura 13).
Podemos generalizar que para cualquier valor de x real positivo el área es
Figura 13.
Deriva la función A2 ( x )
x2
.
2
¿Qué función obtuviste?
¿Tiene alguna relación con la función A1(x) = x?
17
Es la misma función y si ahora derivas A1(x) = x obtendrás la función constante 1, que es
la función inicial.
¿Pasará siempre lo mismo con cualquier otra función constante?
Para contestar veamos otro ejemplo.
1
, calculemos las áreas que se forman con esta función, el eje X, el eje Y y las
2
rectas x = 1, x = 2, x = 3,..., x = 10.
Si f ( x )
Figura 14.
Pon los datos y los resultados de las áreas en los espacios vacíos de la tabla 3.
Tabla 3.
x
1
2
3
4
5
6
7
8
9
10
ƒ(x)
18
A1(x)
Ahora podemos ver el área como una función que depende del valor de x, esto es,
1
A1 ( x ) x , que es una función lineal. Su gráfica es:
2
Figura 15.
En esta gráfica de nuevo podemos calcular el área comprendida entre la función
1
A1 ( x ) x , el eje X y las rectas x = 1, x =2, x = 3,..., x = 10, respectivamente.
2
Figura 16.
Haz la gráfica de las áreas para x = 5 y x = 8.
19
Tabla 4.
x
1
2
3
4
5
6
7
8
9
10
ƒ(x)
1
2
1
2
A1(x)
1
2
A2(x)
1
4
1
1
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
3
2
9
4
2
4
5
2
25
4
3
9
7
2
49
4
4
16
9
2
81
4
5
25
La tabla 4 muestra el valor de todos los cálculos de las áreas. De éstas, la columna 4
1
nos induce a otra función, A2 ( x ) x 2 . Deriva esta función dos veces y observa el
4
resultado en cada caso.
¿El cálculo de las áreas parciales bajo las gráficas de las funciones cuadráticas nos
conducirá a una función cúbica?
¿Cómo calcularemos áreas de regiones irregulares?
20
ACTIVIDAD DE REGULACIÓN
Resuelve los siguientes ejercicios.
1. Sea f(x) = 3, calcula las áreas que se forman con esta función, el eje X, el eje Y y las
rectas x = 1, x = 2, x = 3,…, x = 10.
2. Escribe la función área como una función que depende del valor de “x” y construye su
gráfica. Llámale A1(x) =
3. ¿Qué forma tiene la gráfica?
4. Calcula las áreas que se forman con la función A1(x), el eje X, el eje Y y las rectas x =
1, x = 2, x = 3,…, x = 10.
5. ¿Los resultados anteriores nos inducen a otra función? Si es así, ¿Cuál es?
6. Deriva esta función dos veces y observa el resultado en cada caso.
EXPLICACIÓN INTEGRADORA
Con base en estos ejemplos podemos generalizar, es decir, cualquier función constante
al calcular sus áreas parciales nos conduce a una función lineal de la cual también
podemos ir calculando las áreas en relación con éstas, que nos lleva a una función
cuadrática.
La integral es la operación inversa de la derivada, lo cual se advierte en los dos
ejemplos analizados.
Llamaremos Integral Definida al valor del área bajo una curva en un intervalo.
21
1.2 ÁREA BAJO LA GRÁFICA DE UNA CURVA
Se ha calculado el área bajo la gráfica de ciertas funciones elementales, de cierto modo
sencillo, que son de tipo lineal, es decir, son rectas o segmentos de recta y el cálculo de
las áreas se reduce a determinar el área de rectángulos o triángulos.
Del cálculo del área con base en la gráfica de la función constante f ( x ) 1 , resulta la
función A1 ( x ) x . Y al calcular el área bajo la gráfica de la función A1 ( x ) x , obtenemos
la función A2 ( x )
x2
.
2
También vimos que si derivamos la función A2(x) con respecto a x, obtenemos la función
A1(x) = x; es decir,
dA2 ( x )
dx
x2
2 2x x
dx
2
d
Mas si derivamos la función A1(x) = x con respecto a x, obtenemos f (x ) , esto es:
dA1 ( x )
dx
1
dx
dx
Es decir, la función de donde partió el cálculo.
Para calcular el área bajo la gráfica de una función que no sea necesariamente lineal,
esto es, el área bajo la gráfica de una curva, usaremos el método de exahución, que
sirve para determinar áreas de regiones que no sean de tipo poligonal, sino curvo, como
el círculo. Para esto usaremos tres resultados elementales.
1. El área de un rectángulo es igual al producto de su base por su altura: a = bh .
2. Si tenemos una región conformada por un conjunto de rectángulos adyacentes
que no se traslapan, entonces el área de la región es igual a la suma de las
áreas de cada uno de los rectángulos.
Figura 17.
22
3. Si una región R1 está completamente contenida en una región R2, entonces el
área de R1 es menor o igual que el área de R2, es decir, área de R1 que área
de R2.
Figura 18.
Ahora calcularemos el valor del área bajo la gráfica de una parte de una parábola,
aproximando el área de la región por medio de una sumatoria de áreas de rectángulos
construidos de tal manera que se aproximen cada vez más al área de la región deseada.
2
Sea R la región comprendida entre la gráfica de la función ƒ(x) = x , el eje X y la recta x =
2, construyamos los rectángulos de la siguiente manera:
1. Dividimos el intervalo [0, 2] en 4 subintervalos de igual longitud.
x
20 2
4
4
Esto nos proporciona un conjunto de puntos {x0, x1, x2, x3, x4} con:
x0 0
x1 x 0 x 0
2
2
4
4
x 2 x1 x
2 2
4
4 4
4
x 3 x 2 x
4 2
6
4 4
4
x 4 x 3 x
6 2
8
4 4
4
2 2 4 4 6 6 8
que nos determinan los 4 subintervalos; 0, , , , , , , .
4 4 4 4 4 4 4
23
2. En cada subintervalo construimos un rectángulo con base igual a la longitud del
2
y la altura igual al valor máximo que toma la función en dicho
subintervalo x
4
subintervalo.
Como la función es continua, entonces ésta alcanza su valor máximo en algún punto del
2
intervalo cerrado [a, b]; además, como la función ƒ(x) = x es una función creciente, toma
el valor máximo en el extremo derecho del subintervalo. ¿Por qué?
Figura 19.
Estos rectángulos adyacentes así construidos forman un polígono rectangular
circunscrito P, cuya área es igual a la suma de las áreas de los rectángulos que lo
conforman. El área de cada rectángulo es igual a:
2
2
2 2
A1 f ( x1 )x f x
4
4 4
2
4
4 2
A2 f ( x 2 )x f x
4
4 4
2
6
6 2
A3 f ( x 3 )x f x
4
4 4
2
8
8 2
A4 f ( x 4 )x f x
4
4 4
24
El área del polígono rectangular P es:
2
2
2
2
2 2 4 2 6 2 8 2
P A1 A2 A3 A4
4 4 4 4 4 4 4 4
Tras factorizar y asociar términos tenemos:
3
1
30
2
8
AP 12 2 2 3 2 4 2 1 4 9 16 (30)
3.75
8
8
4
64
Como el polígono rectangular contiene a la región R, entonces tenemos que el área de R
es que el área de P = 3.75.
2 1
; si los cálculos anteriores los hiciéramos con este valor,
4 2
¿cambiaría el resultado?
Observa que x
Si dividimos el intervalo [0,2] en 8 subintervalos, con base en el mismo procedimiento
tenemos:
x
20 2
8
8
2 4 6 8 10 12 14 16
que determina el conjunto de puntos 0, , , , , , , , y los subintervalos:
8 8 8 8 8 8 8 8
2 2 4 4 6 6 8 8 10 10 12 12 14 14 16
0, 8 , 8 , 8 , 8 , 8 , 8 , 8 , 8 , 8 , 8 , 8 , 8 , 8 , 8 , 8 .
Nuestro conjunto de rectángulos lo construiremos con base en la longitud del intervalo y
2
como altura el valor máximo que alcanza la función ƒ(x) = x en cada subintervalo.
25
Figura 20.
2
,
8
donde 2 es la longitud del intervalo que estamos partiendo y 8 es el número de
subintervalos que estamos tomando.
Antes de continuar analicemos más de cerca nuestro procedimiento. Tenemos x
x0 0
x1 x0 x 0
x2 x1 x
2 2
8 8
2 2
2
2
8 8
8
2 2
2
x3 x2 x 2 3
8
8
8
2 2
2
x4 x3 x 3 4
8
8
8
2 2
2
x5 x4 x 4 5
8 8
8
2 2
2
x6 x5 x 5 6
8 8
8
26
2 2
2
x 7 x 6 x 6 7
8 8
8
2 2
2
x 8 x 7 x 7 8
8 8
8
El área de cada rectángulo formado es:
2
3
2 2
2
A1 f ( x 1 )x 12
8 8
8
2
3
2
3
2
3
2
3
2
3
2
3
2
3
2 2
2
A2 f ( x 2 )x 2 2 2
8
8
8
2 2
2
A3 f ( x 3 )x 3 3 2
8
8 8
2 2
2
A4 f ( x 4 )x 4 4 2
8
8
8
2 2
2
A5 f ( x 5 )x 5 5 2
8
8 8
2 2
2
A6 f ( x 6 )x 6 6 2
8
8
8
2 2
2
A7 f ( x 7 )x 7 7 2
8
8 8
2 2
2
A8 f ( x 8 )x 8 8 2
8
8
8
Por lo tanto, el área del nuevo polígono rectangular P será:
AP = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8.
Factorizando y asociando términos tenemos:
3
23
2
AP 12 2 2 3 2 4 2 5 2 6 2 7 2 8 2 3 204 3.1875
8
8
27
De esta expresión vemos que la suma de las áreas de los rectángulos construidos es
igual a la longitud del subintervalo (x) elevado al cubo, multiplicada por la suma de los
cuadrados de los ocho primeros números naturales.
Si partimos ahora el intervalo [0,2] en n = 16 subintervalos tendremos:
x
3
2 2
1
1 2 2 3 2 .... 15 2 16 2
1496 2.9218
16
512
2
16
AP
Si lo dividimos en n = 32 subintervalos tendremos:
x
2
32
3
2 2
1
AP
1 2 2 3 2 .... 312 322
11440 2.7929
32
4096
Si dividimos en n = 64 subintervalos tendremos:
x
2
64
3
2 2
1
AP
1 2 2 3 2 .... 63 2 64 2
89440 2.7294
64
32768
De la operación anterior uno de los factores es la suma de los cuadrados de los 64
primeros números naturales. Como este proceso es muy laborioso, ¿qué ocurre al hacer
la siguiente operación?
64(64 1)2(64) 1
.
6
Compara este resultado con el que ya teníamos.
De aquí en adelante usaremos una operación similar para cada uno de los siguientes
casos.
Si dividimos en n = 128 subintervalos tendremos:
x
2
128
3
1
2 2
AP
1 2 2 3 2 .... 1272 1282
707264 2.6979
128
262144
28
Si dividimos n = 256 subintervalos tendremos:
x
2
256
3
1
2 2
AP
1 2 2 3 2 .... 2552 2562
5625216 2.6823
256
2097152
Si dividimos en n = 512 subintervalos tendremos:
x
2
512
3
1
2 2
AP
1 2 2 3 2 .... 5112 5122
44870400 2.6744
512
16777216
Si dividimos en n = 1024 subintervalos tendremos:
x
2
1024
3
1
2 2
AP
1 2 2 3 2 .... 10232 10242
358438400 2.6705
1024
134217728
2
Ahora calcularemos el área bajo la gráfica de la misma función ƒ(x) = x , comprendida
entre el eje X y la recta x = 3.
Mediante el mismo procedimiento tendremos, para una partición en n = 4 subintervalos.
3
12 2 2 3 2 4 2
3
3
x
AP 12 2 2 3 2 4 2 3 3
4
43
4
Si n = 8 ; x
3
3
8
12 2 2 .... 8 2
3
AP 12 2 2 .... 8 2 3 3
83
8
27(30)
12.6562
64
29
27(204)
10.7578
512
Si n = 16; x
3
3
16
12 2 2 .... 16 2
3
AP 12 2 2 .... 16 2 3 3
163
16
Si n = 32; x
3
3
32
12 2 2 .... 322
3
AP 12 2 2 .... 322 3 3
323
32
Si n = 64; x
3
3
64
3
9.4262
12 2 2 .... 64 2
3
AP 12 2 2 .... 64 2 3 3
643
64
Si n = 128; x
27(1496)
9.8613
4096
3
128
9.2120
12 2 2 .... 1282
3 2
AP
1 2 2 .... 1282 3 3
1283
128
Si n = 256; x
3
3
256
12 2 2 .... 2562
3 2
AP
1 2 2 .... 2562 3 3
2563
256
Si n = 512; x
3
3
512
9.0528
12 2 2 .... 5122
3 2
AP
1 2 2 .... 5122 3 3
5123
512
9.1057
30
9.0263
Si n = 1024; x
3
3
1024
12 2 2 .... 10242
3 2
AP
1 2 2 .... 10242 3 3
10243
1024
9.0131
Al generalizar nuestro procedimiento, se observa que cuanto mayor es el número de
subintervalos en que dividimos el intervalo inicial, menor es el área que resulta de sumar
las áreas de los rectángulos construidos. Para explicarlo analicemos qué sucede en un
subintervalo cualquiera, dada una participación. Tenemos:
Figura 21.
Al duplicar en cada paso el número de subintervalos, significa que para la siguiente
participación el intervalo [xk1,xk] lo dividimos en 2; y al construir los nuevos rectángulos
eliminaremos una parte original.
En la siguiente partición el intervalo queda dividido en 4 subintervalos, con lo cual al
construir los nuevos rectángulos eliminamos otra parte del área original.
Al dividir nuevamente el intervalo en 8 subintervalos y construir los rectángulos
eliminamos otra parte del área original.
Por lo tanto, para cada nueva partición del área del polígono rectangular construido se va
reduciendo, ajustándose al área que deseamos calcular. Cuando el número de
subintervalos es muy grande (n muy grande) entonces el área del polígono rectangular,
así construido, es prácticamente igual al área bajo la gráfica de la función.
31
2
Si calculamos ahora el área bajo la gráfica de la función ƒ(x) = x , el eje X y la recta x =
b, tenemos:
Figura 22
1. Dividimos el intervalo [0, b] en n subintervalos x
partición x 0 , x1,.....,x n con.
x0 0
x1 x 0
b b
n n
x 2 x1
b
b
2
n
n
x3 x2
b
b
3
n
n
.
.
.
x n x n 1
b
b
n b
n
n
32
b
. Esto nos proporciona la
n
Y las áreas de los rectángulos son:
2
b3
b b
A1 f ( x 1 )x 3
n
n n
2
b3
b b
A2 f ( x 2 )x 2 2 2 3
n
n n
2
b3
b b
A3 f ( x 3 )x 3 3 2 3
n
n n
.
.
.
2
b3
b b
An f ( x n )x n n 2 3
n
n n
Sumando estas áreas y factorizando tenemos:
A A1 A2 A3 ... An
b3 2
1 2 2 3 2 ... n 2
n3
12 2 2 3 2 ... n 2
A b 3
n3
Para determinar cada valor debemos establecer qué valor toma la cantidad entre
paréntesis cuando n es muy grande.
n n 1
. De
2
acuerdo con esta expresión ¿habrá una expresión general que nos dé la suma de los
2
2
2
2
cuadrados de los n primeros números naturales?, es decir, 1 + 2 + 3 + ... + n = ?
Como recordarás de tus fascículos de primer semestre, 1 + 2 + 3 +...+ n =
¡Sí! Esta sumatoria es igual a: 12 2 2 3 2 ... n 2
nn 12n 1
6
Demuestra esta fórmula mediante el método de inducción matemática.
33
Sustituyendo la expresión anterior en la fórmula del área, tenemos:
nn 12n 1
A b3
6n 3
Efectuando el producto y la división indicados nos queda:
1
1
1
A b3
2
3 2n 6n
Cuando n es muy grande (n ), el segundo y tercer término dentro del paréntesis
tienden a ser cero; por consiguiente:
A
Si b = 1 ; A
1
0.3333 ;
3
Si b = 2 ; A
8
2.666 ;
3
Si b = 3 ; A
27
9.00 .
3
b3
.
3
Compara estos valores con los obtenidos anteriormente.
Si b = x, entonces el área es una función de x, esto es,
2
Si la función es ƒ(x) = x ; entonces su área es A( x )
x3
.
3
¿Qué obtienes si derivas la función A(x) con respecto de x?
Determinemos por medio del mismo procedimiento el área bajo la gráfica de la función
3
ƒ(x) = x , el eje X y la recta x = b.
1. Partimos el intervalo [0, b] en n subintervalos: x
34
b
n
Obtenemos la partición:
x0 0
x1 x 0
b b
n n
x 2 x1
b
b
2
n
n
x3 x2
b
b
3
n
n
.
.
.
x n x n 1
b
b
n b
n
n
3
2. En cada subintervalo tomemos el valor máximo que alcanza la función ƒ(x) = x .
Como esta función es creciente, el máximo lo alcanza en el extremo derecho de cada
subintervalo. ¿Por qué?
Construyamos el conjunto de rectángulos de base igual a la longitud del subintervalo y
altura igual al valor máximo de la función en el subintervalo; por consiguiente, sus áreas
son:
3
b4
b b
A1 f ( x 1 )x 4
n
n n
3
b4
b b
A2 f ( x 2 )x 2 2 3 4
n
n n
3
b4
b b
A3 f ( x 3 )x 3 3 3 4
n
n n
.
.
.
3
b4
b b
An f ( x n )x n n 3 4
n
n n
35
Sumando estas áreas y factorizando, tenemos:
A A1 A2 A3 ... An
A
4
4
4
b4
3 b
3 b
3 b
2
3
...
n
n4
n4
n4
n4
13 2 3 3 3 ... n 3
A b 4
n4
Investiga hacia dónde tiende el valor de la cantidad que está entre paréntesis cuando n
es muy grande (n ).
¿Hay una fórmula general que nos da la suma de los cubos de
3
3
3
3
los n primeros números naturales 1 + 2 + 3 + ... + n = ?
ACTIVIDAD DE REGULACIÓN
Practica el método que utilizamos para estudiar el área bajo la parábola en un caso más
sencillo:
1. Calcula el área limitada por la función identidad f(x) = x, el eje de las abscisas (eje X)
y las rectas x = 0 (eje Y) y x = 20.
¿De qué figura geométrica se está pidiendo el área?
¿Podrías haber calculado el área bajo la curva más fácilmente?
36
1.3 INTEGRAL DEFINIDA
Ahora calcularemos el área bajo la gráfica respecto de una función ƒ(x) cualquiera.
1. Sea ƒ(x) una función continua en el intervalo cerrado [a, b]
2. Tomemos una partición del intervalo [a, b] en n subintervalos de igual magnitud:
x
ba
n
Esto nos proporciona un conjunto de puntos {x0, x1, x2,...,xn} que conforman un conjunto
de intervalos cerrados [x0, x1], [x1, x2], [x2, x3],..., [xn1,x n].
Con x0 = a
x1 = a + x
x2 = x1 + x = a + 2∆x
.
.
.
ba
b
xn = xn-1 + x = a n
n
3. Construyamos una serie de rectángulos cuya base sea igual a la longitud de los
subintervalos y cuya altura sea igual al valor que toma la función en un punto
cualquiera vk de cada subintervalo [xk1, xk].
Figura 23
37
Esta serie de rectángulos nos determina un polígono P cuya área será igual a la suma de
las áreas de los rectángulos así construidos.
A1 f (v 1 )x
A2 f (v 2 )x
A3 f (v 3 )x
.
.
.
An f (v n )x
Ap A1 A2 A3 ... An f (v 1 )x f (v 2 )x f (v 3 )x ... f (v n )x
4. Tomamos particiones con un número n cada vez más grande de subintervalos; es
decir, que sumaremos las áreas de una infinidad de rectángulos con áreas
infinitamente pequeñas ya que al incrementarse el número de subintervalos x
tiende a ser muy pequeño.
Por lo tanto, si
lìm f (v 1 )x f (v 2 )x f (v 3 )x ... f (v n )x
n
Existe, entonces este límite será igual al área bajo la gráfica de la función ƒ en el
intervalo [a, b] y a esta cantidad le llamaremos integral definida de la función ƒ en el
Intervalo [a,b]; la denotaremos por
b
a
f ( x )dx , es decir,
b
a
f ( x )dx lìmf (v 1 )x f (v 2 )x f (v 3 )x ... f (v n )x
n
x 0
Al símbolo
se le llama integral; a, b se conocen como límite inferior y superior
respectivamente.
38
La expresión
b
a
f ( x )dx se lee, integral de “a” a “b” de la función ƒ(x).
Donde, dx es la diferencial de “x” y se considera una cantidad infinitamente pequeña. La
diferencia es que x la usamos cuando tenemos sumas finitas y dx cuando tenemos
sumas infinitas, es decir, límites.
La función ƒ(x) pude tomar valores negativos, entonces ƒ(vk)x pueden ser cantidades
negativas. Gráficamente esto nos induciría a que el rectángulo construido está por
debajo del eje X y el área del rectángulo estaría multiplicando por –1.
Esto nos lleva a la siguiente conversión: si la región bajo la gráfica está sobre el eje X
ƒ(x)>0 desde x = a hasta x = c, su área es
c
a
f ( x )dx , que es un valor positivo, pero si la
región entre la gráfica y el eje X está por debajo de éste ƒ(x)<0 desde x = c hasta x = b,
el área estará dada por
b
c
f ( x )dx .
Figura 24.
39
ACTIVIDAD DE REGULACIÓN
Calcula el área de las siguientes funciones aplicando el “método de exhaución”.
1)
2)
EXPLICACIÓN INTEGRADORA
Estamos andando sobre un camino que otros hicieron y que ha sido ya bastante
suavizado, podemos incluso aspirar a sintetizar todo este trabajo en un par de ideas:
1. la integral es un método para definir el área de una figura mediante aproximaciones
sucesivas.
2. Las aproximaciones están dadas por medio de rectángulos con la base en el dominio
de la función y con altura determinada de tal manera que el área de cada rectángulo
se asemeje lo más posible al área de la función correspondiente a la base del
rectángulo.
40
1.4 PROPIEDADES DE LA INTEGRAL DEFINIDA
A partir de la definición de la Integral Definida podemos establecer las siguientes
propiedades.
Sean ƒ(x) y g(x) funciones integrales en el intervalo [a,b].
1.
2.
a
a
f ( x )dx 0 ; si f(a) existe
b
b
a
a
cf ( x )dx c f ( x )dx
La integral de una constante por una función es igual a la constante por la integral de la
función.
3.
f ( x ) g( x )dx
b
b
b
a
a
a
f ( x )dx g ( x )dx
La integral de una suma (f + g) de funciones es igual a la suma de las integrales.
4. Sea c un punto entre a y b; a < c < b, entonces
b
a
f ( x )dx
c
a
b
f ( x )dx f ( x )dx .
c
Figura 25.
5.
b
a
a
b
f ( x )dx f ( x )dx .
Si cambiamos los límites de la integral entonces el valor de la integral cambiará de signo.
41
Expresando los resultados obtenidos anteriormente en términos de la nueva terminología
tenemos:
1. Si f(x) = 1 ; 0,b ,
2. Si f(x) = x ,
2
3. Si f(x) = x ,
3
4. Si f(x) = x ,
b
0
b
0
f ( x )dx
b
0
f ( x )dx
b
0
b
dx b .
f ( x )dx
f ( x )dx
0
b
xdx
0
b
0
b
0
b2
.
2
x 2 dx
b3
.
3
x 3 dx ?
Con base en estos resultados y de las propiedades de la integral podemos calcular la
2
integral de la siguiente función: ƒ(x) = 3x 2x + 4, sobre el intervalo [0,2].
b
0
f ( x )dx
2
0
(3 x 2 2x 4)dx 3
2
2
23 22
x 2dx 2 xdx 4 dx 3 2 4(2) 8 4 8 12
3 2
0
0
0
2
ACTIVIDAD DE REGULACIÓN
Resuelve los siguientes ejercicios.
1. Interpreta este resultado en cuanto al área bajo la curva, para esto construye la
gráfica de ƒ(x).
3
2
2. Determina el valor de la integral para la función ƒ(x) = x + 3x – 5x + 7, sobre el
intervalo [0,3].
3. ¿La integral de un producto es igual al producto de las integrales?
4. Piensa en la función f(x) = x = g(x), calcula
a) como un producto de integrales.
1
0
f ( x ) g ( x ) dx :
b) multiplica antes las funciones y después calcula la integral.
Del inciso “a” y el “b”, ¿Se obtiene el mismo resultado?
42
EXPLICACIÓN INTEGRADORA
Las propiedades de la integral definida nos sirven para facilitar el cálculo de ésta.
Como recordarás se vieron 5 propiedades.
a
1.
a
2.
b
b
a
a
3.
f ( x ) g( x )dx
4.
a
5.
b
a
a
b
f ( x )dx 0 ; si f(a) existe
cf ( x )dx c f ( x )dx
b
b
b
a
a
a
b
f ( x )dx
c
a
f ( x )dx g ( x )dx
b
f ( x )dx f ( x )dx
c
si a < c < b
f ( x )dx f ( x )dx .
43
1.5 TEOREMA FUNDAMENTAL DEL CÁLCULO
Como se advierte, encontrar el valor de una integral mediante sumas es bastante difícil;
si la función es polinomial podríamos con dificultad determinar su integral; si la función es
más compleja, como ƒ(x) = sen x ó ƒ(x) = x cos x, podríamos auxiliarnos de una
computadora para encontrar las integrales de estas funciones.
Sin embargo existe una relación entre el concepto de derivada y el de integral que nos
permite determinar las integrales de una manera relativamente sencilla. Este método se
basa en el teorema fundamental del cálculo.
Consideremos una función ƒ(x) definida sobre el intervalo [a,b]. Si F(x) es una función tal
dF( x )
que
f ( x ) , entonces F(x) se dice que es una antiderivada o una primitiva de ƒ(x).
dx
df ( x ) dc
0 , es decir, la derivada de una
dx
dx
constante es igual a cero, pero además el resultado inverso también es cierto:
Sabemos que si ƒ(x) = c, entonces
Si
df ( x )
0 , entonces f(x) = c
dx
La definición de antiderivada y el resultado anterior nos lleva a que si ƒ(x) y g(x) son dos
funciones tales que ƒ’(x) = g’(x), o bien ƒ’(x) – g’(x) = 0 equivalente a ƒ(x) – g(x)’ = 0,
significa que ƒ(x) y g(x) difieren a los más en una constante, es decir, ƒ(x) = g(x) + c.
Si ƒ(x) es una función continua en el intervalo cerrado [a,b], entonces la función F(x)
definida como
x
F ( x ) f ( x )dx con x [a,b]
a
Figura 26.
44
Es una función continua y derivable, ya que:
x
dF( x ) d a f ( x )dx
f (x) ;
dx
dx
es decir, F(x) es una antiderivada o función primitiva de ƒ(x),
F ’(x) = ƒ(x) .
Esto concuerda con los resultados obtenidos en los cálculos que hemos hecho en este
fascículo.
Sea G(x) una antiderivada de la función ƒ(x), esto es,
G’(x) = ƒ(x) ,
Entonces como F(x) =
x
a
f ( x )dx es tal que F ’(x) = ƒ(x) ,
tenemos
F ’(x) = G’(x).
Lo anterior implica que F(x) y G(x) son funciones que difieren a lo más de una constante,
por lo tanto,
F(x) = G(x) + C.
Como F(a) =
a
a
f ( x )dx 0 (primera propiedad de la integral), entonces
0 = F(a) = G(a) + C;
por lo tanto, G(a) + C = 0; C = –G(a); es decir, el valor de la constante C es igual a
menos el valor que toma la función primitiva en el punto “a” y:
F(b) =
b
a
f ( x )dx G(b) G(a) .
Si G(x) es una función primitiva de ƒ(x), entonces
b
a
f ( x )dx G(b) G(a)
A este resultado, el teorema fundamental del cálculo, llegaron Newton y Leibniz.
45
Este teorema nos facilita el cálculo de la integral de muchas otras funciones, como lo
podrás comprobar en los siguientes fascículos. En particular como
d
Esto es,
x n 1
n 11
n 1 n 1 x
xn
dx
(n 1)
x n 1
n
es antiderivada de x , por lo tanto, tenemos:
(n 1)
b
a
b
x n dx
x n 1
b n 1
a n 1
(n 1) a
(n 1) (n 1)
que es congruente con los resultados obtenidos y que nos permite calcular integrales de
6
4
2
funciones tales como ƒ(x) = 5x – 7x + 2x – 5, en el intervalo [2,3].
3
2
f ( x )dx
5
3
3
2
x 6 dx 7
2
(5x 6 7x 4 2x 2 5)dx
3
x 4 dx 2
2
3
2
x 6 1
x 4 1
x 21
2
7
5
2 1 5 x
4 1
6 1
5 x 7 7 x 5 2x 3
5x
7
5
3
3
x 2 dx 5 dx
2
3
2
3
2
5( 2) 7 7( 2) 5 2( 2) 3
5(3) 7 7(3) 5 2(3) 3
5(3)
5( 2)
7
5
3
5
3
7
1562.14 340.2 18 15 91.42 44.8 21.33 10
1282.89
46
ACTIVIDAD DE REGULACIÓN
Calcula la integral de las siguientes funciones en los intervalos indicados.
2
1. ƒ(x) = 4x – 5x + 2 ; [–4,5]
3
2. ƒ(x) = 3x – 2x ; [–3,3]
4
2
4
3
2
6
4
3
3. ƒ(x) = 2x – 7x + 2 ; [–4,4]
4. ƒ(x) = 5x – 3x + 2x – 5x ; [1,2]
5. ƒ(x) = 6x – 4x + 2x – 3x ; [–1,1]
EXPLICACIÓN INTEGRADORA
La integral de funciones polinomiales se puede obtener por medio del Teorema
Fundamental de Cálculo, mediante la aplicación de la siguiente propiedad.
b
a
b
x n dx
x n 1
b n 1
a n 1
(n 1) a
(n 1) (n 1)
47
RECAPITULACIÓN
El siguiente esquema te proporcionará los elementos necesarios para elaborar una
Recapitulación.
Área bajo la gráfica de una recta
Área bajo la gráfica de una curva
Integral Definida
Área bajo la gráfica de una curva
48
ACTIVIDADES DE CONSOLIDACIÓN
1. Calcula el área bajo la gráfica de la función ƒ(x) = 2 sobre el eje X, entre el eje Y
y las rectas x = 1, x = 2, x = 3,..., x = 10.
2. Calcula por el método de exahución el área bajo la gráfica de la función
2
ƒ(x) = 25 – x ; sobre el eje X, entre el eje Y y la recta x = 4. Para construir los
rectángulos toma el valor mínimo de la función en cada subintervalo.
3. Calcula por medio del método de exahución el área de la región determinada por
3
la gráfica de la función ƒ(x) = x ; el eje X y las rectas x = –2 y x = 2.
Figura 26.
49
En los siguientes ejercicios utiliza las propiedades de la integral, el Teorema
Fundamental del Cálculo y el resultado
b
a
x n dx
x n 1
n 1
b
para determinar el valor de la
a
integral que se te pide.
2
4. Sea ƒ(x) = 3x – 2x + 1 ; [0,5]
5
3
7
4
5. Sea ƒ(x) = 4x – 6x + 3x ; [–2,2]
2
6. Sea ƒ(x) = x + 8x 3x + 5 ; [–1,2]
7. Sean ƒ(x) = 3x – 2 y g(x) = 2x 3 ;
f ( x ) g( x ) dx
5
0
x 2 si 0 x 2
8. Sea f ( x )
calcula el área bajo la función ƒ(x), sobre el eje X
b si 2 x 4
y la recta y = 4.
Figura 27.
50
AUTOEVALUACIÓN
Con la intención de corroborar tu aprovechamiento se te proporcionan algunas
respuestas a las Actividades de consolidación.
1. Ya que ƒ(x) = 2 es una función constante, ¿puedes tomar el extremo derecho de
cada subintervalo para tener la altura de los rectángulos? ¿Cuál es la altura de
éstos?, ¿cuál es su base?, ¿sucede lo mismo para las rectas x = 2, x = 3,..., x =
10? Abreviando el desarrollo:
2
Para x = 1 el área es A1 = 2 u
2
x = 2 el área es A2 = 4 u
2
x = 3 el área es A3 = 6 u
.
.
.
2
x = 10 el área es A10 = 20 u .
2. ¿Se llegará al mismo resultado si tomamos los máximos de la función en cada
uno de los subintervalos?
3
3. Como ƒ(x) = x toma valores negativos en el intervalo [2,0]; el valor de la
integral será negativo. Además, por la simetría de la gráfica, el área por arriba
del eje X es igual al área por abajo del eje X. Entonces, ¿Cuál es el valor de la
integral? ¿Cómo puede determinarse el área verdadera? ¿cuál es la propiedad
de la integral que te permite lograr esto?
Después de haber realizado tu desarrollo, conforme a lo anterior, compara tú
resultado con:
2
Área = 8 u .
51
2
4. 105 u
5. 0
6.
1077 2
u
40
7.
75 2
u
2
8.
32 2
u
3
52
ACTIVIDADES DE GENERALIZACIÓN
Se recomienda visitar el Museo de las Ciencias “Universum”, donde encontrarás
diferentes apoyos para la comprensión analítica de las cuestiones básicas de las
Matemáticas.
También te sugerimos ver la película con ganas de triunfar (que se proyecta en varios
planteles del Colegio de Bachilleres) para tener actitud crítica y reflexiva en cuestiones
relacionadas con el cálculo.
53
BIBLIOGRAFÍA CONSULTADA
ANFOSSI, A. Y Fores Meyer M. A. Cálculo Diferencial e Integral, 9ª. Ed. Progreso,
México, 1954.
BOSCH, Guerra, Hernández y Oteyza. Cálculo Diferencial e Integral. Publicaciones
Cultural, México, 1995.
CRUSE, A.B. y Lehman M. “Introducción a la Integral”, en Lecciones de Cálculo 2. Fondo
Educativo Interamericano, México, 1982.
GÓMEZ, José Luis. Introducción al Cálculo Diferencial e Integral, 2ª. Ed. Limusa, México,
1987.
HOCKETT, Shirley O. y Sternstein Martín. Cálculo por objetivos y aplicaciones. CECSA,
México, 1985.
LARSON, Hostetler. Cálculo y Geometría Analítica. McGraw-Hill, México, 1986.
SALAS, S.L. y Hille E. Cálculos de una y varias variables, 2ª. Ed. Reverté, España,
1982.
SWOKOWSKI, E.W. Cálculo con Geometría Analítica. Iberoamérica, México, 1979.
WENZELBURGER, E. Cálculo
Iberoamericana, México, 1985.
Integral.
Módulo
introductorio.
Universidad
Revista del Seminario de Enseñanza y Titulación, año II, núm. 6, diciembre de 1985.
54
COLEGIO DE BACHILLERES
CÁLCULO DIFERENCIAL
E INTEGRAL II
FASCÍCULO 2. LA INTEGRAL INDEFINIDA
Autores: Luisa Guerrero Chávez
Alejandro Jesús López Argüelles
Alberto Luque Luna
María del Carmen Santoveña
Delgado
Mauro Enrique Vázquez Muñoz
Miguel Ángel Villagómez Aragón
2
Í N D I C E
INTRODUCCIÓN
7
CAPÍTULO 1. INTEGRAL INDEFINIDA
9
PROPÓSITO
11
1.1 ANTIDERIVADA O FUNCIÓN PRIMITIVA
16
1.2 CONCEPTO DE INTEGRAL INDEFINIDA
20
1.3 CONSTANTE DE INTEGRACIÓN
25
1.4 DETERMINACIÓN DE LA CONSTANTE
30
1.5 COMPARACIÓN ENTRE INTEGRAL
INDEFINIDA Y DEFINIDA
37
1.6 ALGUNOS CASOS BÁSICOS DE
INTEGRALES INDEFINIDAS
40
RECAPITULACIÓN
ACTIVIDADES INTEGRALES
AUTOEVALUACIÓN
47
3
48
49
CAPÍTULO 2. TÉCNICAS DE INTEGRACIÓN
51
PROPÓSITO
53
2.1 CAMBIO DE VARIABLE
57
2.2 INTEGRACIÓN POR PARTES
62
2.3 INTEGRACIÓN DE FUNCIONES
RACIONALES POR DESCOMPOSICIÓN EN
FRACCIONES PARCIALES
68
2.3.1 DENOMINADOR FORMADO POR UNA
FUNCIÓN LINEAL
2.3.2 DENOMINADOR FORMADO POR FACTORES
LINEALES DE PRIMER GRADO QUE NO SE
REPITEN
2.3.3 DENOMINADOR FORMADO POR FACTORES
DE SEGUNDO GRADO QUE NO SE REPITEN
RECAPITULACIÓN
ACTIVIDADES INTEGRALES
AUTOEVALUACIÓN
ANEXO
CAPÍTULO 3. APLICACIONES DEL CÁLCULO
INTEGRAL
68
71
75
81
82
83
84
87
PROPÓSITO
89
3.1 VALOR PROMEDIO DE UNA FUNCIÓN Y
ÁREA BAJO LA CURVA
92
3.2 INTEGRAL DE LA RAZÓN DE CAMBIO
INSTANTÁNEA
100
3.3 ÁREA BAJO LA CURVA
112
3.4 ÁREA ENTRE CURVAS: UTILIDADES
119
3.5 CÁLCULO E INTERPRETACIÓN DE LA
CONSTANTE DE INTEGRACIÓN
131
4
RECAPITULACIÓN
ACTIVIDADES INTEGRALES
AUTOEVALUACIÓN
138
139
140
RECAPITULACIÓN GENERAL
141
ACTIVIDADES DE CONSOLIDACIÓN
142
AUTOEVALUACIÓN
144
ACTIVIDADES DE GENERALIZACIÓN
146
BIBLIOGRAFÍA CONSULTADA
151
5
6
I N T R O D U C C I Ó N
Este Fascículo consta de tres capítulos:
En el capítulo 1. Integral Indefinida, se plantea desde lo que es el concepto de integral,
pasando por lo que es la determinación de la constante, así como la comparación entre
integral definida (Fascículo 1) e integral indefinida, sin olvidar, por supuesto, algunos
ejemplos básicos de integrales indefinidas.
Una de las mejores maneras de aprender el Cálculo es a base de resolver ejercicios y/o
problemas, y que mejor para el logro del objetivo que aventurarnos en el capítulo 2
referente a las Técnicas de Integración.
Por último, para reforzar lo aprendido del capítulo 1 y 2, se presentan en el capítulo 3
una serie de problemas muy interesantes de las aplicaciones del Cálculo Integral en el
campo de la Física, Biología, Ingeniería, Economía y Medicina.
7
8
C A P Í T U L O
1
INTEGRAL INDEFINIDA
1.1 ANTIDERIVADA O FUNCIÓN PRIMITIVA
1.2 CONCEPTO DE INTEGRAL INDEFINIDA
1.3 CONSTANTE DE INTEGRACIÓN
1.4 DETERMINACIÓN DE LA CONSTANTE DE INTEGRACIÓN
1.5 COMPARACIÓN ENTRE INTEGRAL INDEFINIDA Y DEFINIDA
1.6 ALGUNOS CASOS BÁSICOS DE INTEGRALES INDEFINIDAS
9
10
PROPÓSITO
El cálculo diferencial y el cálculo integral son procesos inversos cuyo análisis de relación
se alcanza con el contenido del presente fascículo, el cual pretende que al concluir su
estudio:
¿QUÉ APRENDERÁS?
El Teorema Fundamental del Cálculo y a
resolver integrales indefinidas y definidas.
¿CÓMO LO APRENDERÁS?
Mediante la relación existente entre
ambas integrales y el procedimiento de
evaluación y solución de dichas integrales
¿PARA QUÉ TE VA A SERVIR?
Para evaluar una integral definida (área
bajo una curva) de funciones elementales
y para determinar el valor de la constante
de
integración
que
se
indica
explícitamente en cada integral indefinida.
11
12
CAPÍTULO 1
LA INTEGRAL INDEFINIDA
A continuación te presentamos un ejemplo que te ayudará a comprender el concepto de
la integral indefinida.
Durante un recorrido en autobús, un estudiante observó que el velocímetro marcaba 15
km/h y que este trayecto se hizo en una hora; al llegar a una parte de subidas y curvas la
velocidad era de 40 km/h, y al salir de éstas la velocidad era de 60 km/h. Al circular en la
autopista, la velocidad era de 90 km/h. Con estos datos el observador hizo la siguiente
gráfica.
Figura 1.
13
Esta gráfica representa los cambios de velocidad en un intervalo de tiempo, pero no dice
cuántos kilómetros son, ya que son resultados acumulados de razones de cambio, mas
al tomar la suma de los productos de las razones de cambio multiplicados por el intervalo
el resultado obtenido será la suma total de los procesos de cambio. Por consiguiente,
para obtener la distancia total se tiene:
15 km/h(1h) + 40 km/h(1h) + 60 km/h(1h) + 90 km/h(1h);
Entonces la distancia resulta:
15 km + 40 km + 60 km + 90 km = 205 km.
La figura 2 representa la distancia total recorrida en 4 h.
Figura 2.
De acuerdo con las gráficas se puede establecer que obtener la distancia que recorre el
autobús implica sumar o integrar esas razones de cambio simbólicamente, por lo tanto,
vdt s
función desplazamiento
función velocidad
O inversamente, si es la distancia o desplazamiento lo que se tiene y deseas obtener la
ds
velocidad, debes derivar la función desplazamiento
v.
dt
14
Lo anterior es una explicación que te ayudará a entender el porqué de ciertas funciones
continuas; por ejemplo:
y
2
(1) ƒ(x) = x , cuya gráfica es:
x
0
y
2
(2) ƒ(x) = x + 2, cuya gráfica es:
x
0
y
2
(3) ƒ(x) = x – 2, cuya gráfica es:
x
0
Al derivar obtienes otra función: ƒ’1(x) = 2x, ƒ’2(x) = 2x y ƒ3(x) = 2x , que al integrarlas se
regresa a las funciones (1), (2) y (3).
15
1.1 ANTIDERIVADA O FUNCIÓN PRIMITIVA
A lo largo de tu formación académica has observado que en Matemáticas existen
operaciones y funciones inversas, algunos ejemplos se especifican en la siguiente tabla:
Respecto a la derivada y la antiderivada, se manejarán como procesos inversos.
En los conceptos estudiados en Cálculo Diferencial hay uno que plantea el siguiente
problema: dada una función, encontrar su derivada, que en Cálculo Integral
estudiaremos como el problema inverso: dada la derivada de una función, hallar la
función original o primitiva. Supongamos que deseamos encontrar una función F(x) que
tiene como derivada a:
dF( x )
2
3x
dx
Se diría que:
F ( x ) x 3 porque
dF( x ) dx 3
3x 2
dx
dx
o podemos decir que:
F1( x ) x 3 4 porque
16
dF1 ( x )
3x 2
dx
Las gráficas serían:
Figura 3.
De acuerdo con lo anterior, si llamamos a la función F(x) antiderivada o primitiva,
3
2
decimos que x es antiderivada o primitiva de 3x .
La derivación y la antiderivación, que se consideran procesos inversos, podemos
esquematizarlas como sigue:
ƒ(x) es una
función que
da una razón
de cambio.
Integración
Integrando
la razón de
cambio se
obtienen
sus efectos
acumulados
, F(x).
Derivación
Derivando
los
efectos cumulados
se obtiene la razón
de cambio original,
ƒ(x).
De acuerdo con el esquema, F(x) es una antiderivada o primitiva de ƒ(x) en un lugar de
la antiderivada o primitiva de ƒ(x). ¿Por qué?
2
Una antiderivada o primitiva de ƒ(x) = 2x es F(x) = x , puesto que
2
2
dF( x )
2x
dx
Incluso podemos decir que F1(x) = x – 1 y F2(x) = x + 10 son antiderivadas o primitivas
de ƒ(x) = 2x, puesto que
dF1( x ) dF2 ( x )
f (x)
dx
dx
17
Si F(x) es un antiderivada (primitiva) de una función ƒ(x), entonces G(x) = F(x) + C
también lo es. Aquí C representa una constante (valor independiente de x) y G(x) es otra
función cualquiera.
¿Por qué G(x) también es una antiderivada o primitiva? Si suponemos que G(x) es una
antiderivada o primitiva entonces concluimos que:
dG( x )
f (x)
dx
Hemos dicho que G(x) = F(x) + C, más si derivamos se tendrá:
dG( x ) dF( x ) C dF( x ) dC dF( x )
0 f (x)
dx
dx
dx
dx
dx
Por lo tanto,
de ƒ(x).
dG( x )
f ( x ) . Por consiguiente, G(x) es una antiderivada o función primitiva
dx
De esto concluimos que la antiderivada (o primitiva) de ƒ(x) debe tener la forma G(x) =
F(x) + C, es decir, dos antiderivadas de la misma función pueden diferir cuando más en
una constante.
En adelante se hará referencia a F(x) + C como la antiderivada de ƒ(x). Además, F(x) +
C representa un conjunto de funciones del cual cada miembro tiene por derivada a ƒ(x),
y C tendrá valores diferentes.
ACTIVIDAD DE REGULACIÓN
¿Cuál es la operación inversa de la integración?
18
EXPLICACIÓN INTEGRADORA
Función Primitiva F(x). Es la función que se obtiene al integrar la función original f(x).
Así,
Si F(x) es una función primitiva de f(x)
entonces
La derivada de F(x), será la función original
19
d F(x)
f (x)
dx
1.2 CONCEPTO DE INTEGRAL INDEFINIDA
Si F(x) y G(x) son antiderivadas o primitivas de ƒ(x) que difieren cuando más en una
constante, podemos decir que al derivar la función primitiva obtendremos la función
original, esto es:
F’(x) = ƒ(x),
O bien
dF( x )
f (x)
dx
Lo anterior puede expresarse como:
dF(x) = ƒ(x)dx
o
dF(x) = F’(x)dx
La operación para encontrar todas las soluciones de la ecuación anterior se llama
antiderivación o integración, y se representa por
estilizada.
, que es una sigma mayúscula
Así, podemos representar la solución como
f ( x )dx = F(x) + C,
donde f ( x )dx se lee como la integral o antiderivada de ƒ(x) respecto a x.
De acuerdo con la simbología:
ƒ(x) es el integrando
es el signo de integral
ƒ(x)dx es el elemento de integración
C es la constante de integración
20
2
2
Recuerda que F1(x) = x 1 y F2(x) = x + 10 son dos antiderivadas o primitivas de la
función ƒ(x) = 2x, pero ¿son las únicas? Para responder, de la función ƒ(x) = x
obtengamos sus antiderivadas o primitivas.
antiderivada de x es
x2
2
porque la derivada de
x2
es x
2
antiderivada de x es
x2
1
2
porque la derivada de
x2
1 es x
2
antiderivada de x es
x2
7
2
porque la derivada de
x2
7 es x
2
antiderivada de x es
x2
11
2
porque la derivada de
x2
11 es x
2
antiderivada de x es
x2
4
2
porque la derivada de
x2
4 es x
2
¿Hay otras antiderivadas o primitivas de la función ƒ(x) = x ?
¿Podrías demostrar que hay otras expresiones antiderivadas de x ?
Haz el ejercicio anterior con base en la derivación como comprobación. Nos referimos a:
Una antiderivada de x es
d x2 d
x2
8 x 0 x
8 , porque
2
dx 2 dx
Para los ejemplos anteriores se debe entender que aunque la función ƒ(x) = x tiene un
número infinito de antiderivadas o primitivas, hay una parte de todas ellas que
permanece:
x2
2
Así podemos escribir todas las antiderivadas o primitivas de x con base en la siguiente
notación.
Antiderivada de x es
x2
C ,
2
donde C es un número que llamaremos constante de integración.
21
La ecuación anterior se expresa en forma simbólica como:
xdx
x2
C que es la antiderivada o integral indefinida.
2
Es decir, para indicar una antiderivada o primitiva o integral indefinida de una función
general ƒ(x) es común encontrarla con la siguiente simbología:
f ( x )dx F ( x ) C ,
llamada integral indefinida de la función ƒ(x).
Pero, ¿por qué una función puede tener un número infinito de antiderivadas? Se darán
dos respuestas: una analítica y otra geométrica.
La primera es simple, pues la hemos estado usando: por ejemplo, recuerda que
habíamos mencionado a:
x2
7
2
y
x2
11
2
como algunas de las antiderivadas de la función ƒ(x) = x. Esto se comprueba derivando
ambas fórmulas, como ya se había indicado.
De éstos dos ejemplos se deduce que podemos añadir una constante arbitraria de
integración porque la derivada de la constante es cero. Cualquiera que sea el valor de la
constante, no tiene efecto al calcular la derivada.
La respuesta geométrica está en razón de la interpretación de la derivada como una
pendiente. La figura 4 muestra tres diferentes curvas, cada una de las cuales tiene la
misma derivada, mostrada en la figura 5. Así, la antiderivada de x representa una familia
x2
C .
de funciones, todas de la forma
2
22
Figura 4.
Figura 5.
23
ACTIVIDAD DE REGULACIÓN
Traza la gráfica de la función f ( x )
x2
2 (utiliza el eje de coordenadas de la figura 4).
2
EXPLICACIÓN INTEGRADORA
Integral Indefinida.
Se llama integral indefinida de la función f(x) al conjunto de todas las primitivas de f(x).
A la integral indefinida se le nota por la expresión:
24
f ( x )dx F ( x ) C
1.3 CONSTANTE DE INTEGRACIÓN
En la figura 4 se observa que la constante C de la antiderivada puede tomar diferentes
valores, que dependen de la función original Recuerda que en Cálculo Diferencial se
daban, por ejemplo, las siguientes funciones:
f (x)
1 2
x 4
2
f (x)
1 2
x 10
2
f (x)
1 2
x 1,
2
que al derivarlas obtenías:
ƒ’(x) = x
ƒ’(x) = x
ƒ’(x) = x
¿Qué pasaba con los valores 4, 10 y 1?
Estos valores, que si bien valen cero en la función derivada, son de gran importancia en
Cálculo Integral, si queremos obtener las funciones originales a partir de las funciones
derivadas.
Para entender lo anterior, además del término constante de integración; pasaremos a las
funciones planteadas en el principio del capítulo, esto es:
ƒ(x) = x
2
(1)
2
(2)
2
(3)
ƒ(x) = x + 2
ƒ(x) = x – 2
Analizando veremos que:
En la función (1) la constante no existe, por lo tanto, es cero.
En la función (2) la constante vale 2.
En la función (3) la constante vale – 2.
25
Para un mejor análisis recurramos al aspecto gráfico, esto es, hacer la gráfica de cada
función (figura 6), Tabularemos la primera función y tú harás las restantes.
ƒ(x) = y = x
2
y=x
2
o
ƒ(x) = x
2
Figura 6.
Obsérvese la posición sobre los ejes x y y de cada una de las gráficas, ¿qué diferencias
y similitudes hay? Para una mejor comprensión de lo que es Cálculo Diferencial e
Integral hagamos lo siguiente:
Al derivar la función (1)
tendremos
dx 2
2x
dx
(1’)
Al derivar la función (2)
tendremos
d x 2 2
2x
dx
(2’)
Al derivar la función (3)
tendremos
d x 2 2
2x
dx
(3’)
Estas derivadas tienen la misma expresión matemática, aun cuando prevengan de
diferente función; mas si recurrimos al proceso inverso, es decir, integramos la función
derivada, entonces:
26
Se integra la función (1’)
2xdx x 2 C , porque
dx 2
2x .
dx
Se integra la función (2’)
2xdx x
2
C , porque
dx 2
2x .
dx
2xdx x
2
C , porque
dx 2
2x .
dx
Se integra la función (3’)
Como la integración es un proceso inverso de la derivación se infiere que al integrar las
funciones (1’), (2’) y (3’) tendríamos las funciones (1), (2) y (3); sin embargo, en los
resultados de la integración no se cumple, ¿por qué?, ¿Qué hace falta para obtener las
funciones (1), (2) y (3)? Se debe agregar a la integral indefinida una constante, C que al
calcularse podremos determinar las funciones (1), (2) y (3), respectivamente. Por lo
tanto, lo correcto es escribir la integración de la siguiente forma:
2xdx x
2xdx x
2
2
2xdx x
2
C ,
donde C = 0
C ,
donde C = 2
C ,
donde C = 2
Se advierte que el valor de C es fácil inferirlo porque ya conocíamos las funciones (1), (2)
y (3); sin embargo, no ocurre así en todos los casos, pues las más veces debemos
indicar la constante, C, cuando efectuamos una integral indefinida. En otros casos se
nos dan algunas condiciones iniciales de la función para determinar el valor de C.
Antes de determinar el valor de la constante es importante ver en forma gráfica la
relación entre la integración y diferenciación. Para esto vemos el siguiente ejemplo.
2
De la función (1), ƒ(x) = x sabemos que su gráfica es una parábola cuyo vértice es el
origen y concavidad hacia arriba; al obtener la derivada resulta otra función que es de
primer grado (una recta). Este proceso se estudió en Cálculo Diferencial (Figura 7a),
pero en Cálculo Integral se tiene el proceso inverso, porque a la función derivada hay
que aplicarle el proceso de integración (Figura 7b).
27
Figura 7a.
ACTIVIDAD DE REGULACIÓN
Analiza la siguiente figura.
Figura 7b.
Al aplicarle la integración a la función f(x) = 2x, ¿Puedes inferir que gráfica obtendrás
correspondiente a la función integrada?
28
EXPLICACIÓN INTEGRADORA
Cuadro en donde se indica el por qué una integral indefinida tiene siempre una
constante.
29
1.4 DETERMINACIÓN DE LA CONSTANTE DE INTEGRACIÓN
Se ha visto que evaluar una integral indefinida implica que hay una constante de
integración C, la cual, al evaluarla, obtendremos la función original. Si retomamos las
2
2
2
funciones ƒ(x) = x , ƒ(x) = x + 2 y ƒ(x) = x – 2, de manera general podemos indicar que
2
y = ƒ(x) = x + C
representa una familia de parábolas y cada valor de C corresponde a una de ellas; por
ejemplo:
2
y=x +2
2
y=x –2
2
y=x –3
2
2
y=x +C ó y=x –C
2
y = x + 1/4
2
y = x + 10
2
y = x – 1/16
2
Se observa que C toma diferentes valores, incluso cero, y toma la forma y = x . A
continuación se indican ciertas condiciones iniciales para determinar el valor de la
constante C.
2
Si queremos que una de las parábolas descritas por la ecuación y = x + C pase por el
punto P(2,1), al sustituir tendremos:
2
y=x +C
si P(2,1) que es condición de la función
2
1=2 +C
1=4+C
C=1–4
C = 3.
2
Entonces se estará hablando de la parábola y = x – 3. Veamos otro ejemplo:
30
2
Si y = x + C y uno de sus puntos es P(1,3) tendremos:
2
y=x +C
2
3=1 +C
3=1+C
C = 2,
2
Y la parábola será y = x + 2
2
Adicionalmente, calcula la constante de y = x + C si queremos que los siguientes puntos
pertenezcan a las parábolas. Comprueba lo anterior trazando las parábolas.
P(3,1)
P(4,3)
P(3,2)
P(3,4)
P(2,5)
P(3,2)
Cuando se conoce la constante de integración, podemos llegar a la función primitiva que
dio origen a la derivada.
Veamos cómo determinar la constante de integración a partir de otro enfoque. Para ello
recuerda lo estudiado en el Fascículo 1, de Cálculo Diferencial e Integral II, donde se
indica que debes:
x
f ( x ) dx
si
f ( x ) 0 en a, x
f ( x ) dx A( x )
si
f ( x ) 0 en a, x
A( x )
a
o bien,
x
a
es decir, en estas circunstancias la integral definida representa geométricamente el área
bajo la curva ƒ(x) cuando x varía en [a, x].
31
En este fascículo se llegó a la expresión de integral indefinida como:
f ( x )dx F ( x ) .
De estas dos expresiones se deduce que las integrales de la misma función difieren
únicamente en una constante, ya que A(x) y F(x) son dos integrales de ƒ(x):
A(x) = F(x) + C ;
Por lo tanto, el siguiente paso es determinar el valor de C, consideremos el área
sombreada bajo ƒ(x) entre las líneas verticales sobre (a,0) y (x,0) de la figura 8.
Figura 8.
Aquí A(a) = 0 es el área del segmento con extremos en (a,0) y (a,ƒ(a)).
Usando A(x) = F(x) + C y cuando x = a:
A(a) = F(a) + C;
pero A(a) = 0
0 = F(a) + C
C = F(a)
De la ecuación anterior recuerda que:
A(x) es el área bajo la curva ƒ(x) en el intervalo [a,x]
F(x) es la integral indefinida
f ( x )dx
F(a) es F(x) evaluada en a.
32
2
Encontremos ahora el área bajo la curva y = x desde 0 hasta x (figura 9).
Figura 9.
Como sabemos
x 2 dx
x3
C F(x)
3
A(x) = F(x) – F(0);
Pero F ( x )
y F(0 )
x3
C
3
03
C ;
3
Por lo tanto, al sustituir en A(x),
x3
03
A( x )
C
C
3
3
A( x )
x3
.
3
Observa que la constante, C, se elimina al encontrarse la expresión F(x) – F(a); así,
podemos omitir sencillamente C, como en el siguiente ejemplo:
2
¿Puedes encontrar el área bajo la curva y = 2x , entre los puntos (2,0) y (3,0) de la figura
10?
33
f(x)
x
0
1
2
3
4
Figura 10.
Solución
A(x) = F(3) – F(2),
Donde F(x) = 2x 2 dx =
Así, F(3) =
23
18
3
3
2x 3
3
y
F(2) =
22
16
3
3
3
Al sustituir en la primera expresión, el área es:
A(x) = 18
16 38
.
3
3
Se concluye que si se pide el área limitada por la curva ƒ(x) cuyo intervalo es [a,b] (figura
11), podemos encontrarla con:
A
o bien
b
a
f ( x ) dx
A = F(b) – F(a), siempre que F’(x) = ƒ(x) ó F(x) = f ( x )dx .
La última expresión de A indica que el área también puede encontrarse en términos de la
integral indefinida.
34
Figura 11.
De acuerdo con lo anterior tenemos la relación
b
a
f ( x ) dx F (b) F (a) , si F ( x ) f ( x )dx .
En consecuencia, la integral definida puede expresarse en términos de una integral
indefinida evaluada en los límites.
¿Te es familiar este resultado?
Por supuesto que si, la formalidad de estos ejemplos es lo que se analiza en el Teorema
Fundamental de Cálculo del Fascículo 1.
ACTIVIDAD DE REGULACIÓN
2
Calcula el área bajo la curva y = x entre los puntos (1,0) y (2,0).
35
EXPLICACIÓN INTEGRADORA
36
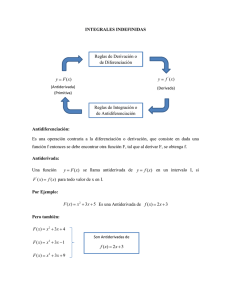
1.5 COMPARACIÓN ENTRE INTEGRAL INDEFINIDA Y DEFINIDA
Es importante establecer la relación entre integrales indefinidas y definidas, ya que son
muy diferentes aun cuando existe una relación estrecha entre ellas.
La integral definida
b
a
Suma [ƒ(x) x] o bien
f ( x ) dx se define en términos del límite de una suma:
[ƒ(x) x].
2
2
La integral definida es un número (frecuentemente en dimensiones como cm o m ) que
se aproxima por términos de sumas cuyo número de rectángulo se hace infinito y el
ancho de la base de los mismos se aproxima a cero.
La integral indefinida
f ( x ) dx es una función cuya derivada es ƒ(x).
Como ejemplo de distinción entre la integral definida e indefinida tenemos:
3
0
x2
2
xdx
3
0
3
0
xdx
cuya gráfica se muestra en la figura 12.
Figura 12.
37
32 02
2
2
9
2
En cuanto a la integral indefinida
x2
C ,
2
x dx
La gráfica correspondiente es la figura 13, que es una familia específica de funciones
donde la diferencia entre cada una es la constante.
Figura 13.
ACTIVIDAD DE REGULACIÓN
Resuelve y evalúa las siguientes integrales:
1.
x
2.
3.
p dp
2
1
3
dx
4.
x 3 dx
5.
y dy
6.
x 1 dx
3
1
q 3 dq
38
EXPLICACIÓN INTEGRADORA
39
1.6 ALGUNOS CASOS BÁSICOS DE INTEGRALES INDEFINIDAS
De la siguiente serie de funciones obtener su antiderivada o primitiva para observar y
deducir su comportamiento.
1. Antiderivada de 1 = x
2. Antiderivada de x
x2
2
3. Antiderivada de x 2
4. Antiderivada de x 3
x4
4
5. Antiderivada de x 4
x5
5
x3
3
¿Puedes dar el patrón de éstas fórmulas? Hay una fórmula para una antiderivada de
n
n+1
cualquier función de la forma x , que siempre es una constante multiplicada por x .
Entonces, cuando derivamos ésta función llegamos a otra función cuyo exponente es
uno menos que el de la función original. Por lo tanto, si antiderivamos una función,
llegamos a una nueva función cuyo exponente es más uno que la función original. Esto
nos lleva a las siguientes fórmulas:
40
Por lo tanto, antiderivada de x n
x3
x 31 x 4
.
3 1
4
x n 1
C . Por ejemplo, si n = 3, antiderivada de
n 1
Que está de acuerdo con el resultado de la tabla.
Si n = 7, entonces de acuerdo con la fórmula antiderivada de:
x7
x 71 x 8
7 1
8
Para comprobar la fórmula general de antiderivada o función primitiva basta con derivar
la siguiente función:
x n 1
y
n 1
de la cual resulta:
y ' n 1
x n 11
xn
n 1
que es la función con la cual empezamos y muestra que la fórmula general es correcta.
La integral de las funciones ƒ(x) = 1 y ƒ(x) = x permite ver el comportamiento de la
integral definida con el de la integral indefinida o antiderivada.
Figura 14.
El área bajo una curva en un intervalo cerrado se calcula por medio de la integral
definida.
b
f ( x ) Área
a
41
Respecto a la figura 14 tenemos ƒ(x) = 1 y el área de un rectángulo es bh (base por
altura), por lo tanto:
b
a
1
0
f ( x ) dx bh
dx (1)(1) 1,
que es el área del rectángulo A1
2
0
dx (2)(1) 2 ,
xn
0
que es el área del rectángulo A2
dx ( x n )(1) x n , que es el área del rectángulo n–simo
De esta integral definida resulta el área del n–simo rectángulo. Para la misma función la
integral indefinida es:
dx x C
En el caso de la integral indefinida para la misma función el resultado no es un número,
es una familia de funciones de la forma x + C.
Figura 15.
El área está definida por:
b
a
f ( x ) dx área
42
En este caso ƒ(x) = x, y el área
bh
(área de un triángulo).
2
Por lo tanto,
b
a
f ( x ) dx
1
0
2
0
x dx
(1)(1) 1
2
2
x dx
(2)( 2) 4
2
2
xn
0
bh
2
xdx
( x n )( x n ) x n
.
2
2
2
De la integral definida resulta un valor numérico, que en este caso representa el área del
triángulo n-simo. Para la integral indefinida de la función ƒ(x) = x se tiene:
xdx
Que representa una familia de funciones
una de esas funciones.
x2
C
2
x2
C donde C es el valor que caracteriza a
2
En los siguientes ejercicios obtendremos la integral indefinida.
1. ƒ(x) = x
4
4. ƒ(x) = x
3
2. ƒ(x) = 1
5. ƒ(x) = x
3. ƒ(x) = cos x
6. ƒ(x) = sen x
Como la integral indefinida es equivalente de antiderivada podemos indicar como:
1. Antiderivada de x
4
4. Antiderivada de x
3
2. Antiderivada de 1
5. Antiderivada de x
3. Antiderivada de cos x
6. Antiderivada de sen x
43
Si lo anterior lo indicamos con una simbología más adecuada, de hecho lo que nos pide
es:
1.
x
4.
xdx
2.
dx
5.
x
3.
cos x dx
6.
senx dx
4 dx
3 dx
Para resolver las integrales recuerda que debemos encontrar una función F(x) tal que:
dF( x )
f (x) .
dx
A fin de resolver la integral 1 podemos hacer uso de la tabla de antiderivadas, por lo
tanto:
x 41 x 5
x 4 dx
C
4 1
5
Con objeto de comprobar que es correcto hacemos:
4
d x5
d x5 d
C 5x 0 x 4 .
C
dx 5
5
dx 5 dx
Entonces:
x
4 dx
x5
C.
5
La integral indefinida de la función 3 es:
cos x dx senx C ,
Porque
d
senx C d senx d C cos x 0 cos x
dx
dx
dx
44
ACTIVIDAD
DE
REGULACIÓN
Obtén la integral indefinida de los ejercicios 2, 4, 5 y 6
La dificultad para encontrar la integral indefinida de una función se resuelve
particularmente para cada función, ya que no hay un método general para resolverla. No
obstante, en ciertos casos es sencillo encontrarla, mediante las derivadas de las
funciones.
En las siguientes propiedades de la integral indefinida se indican dos fórmulas que
pertenecen a la tabla de integrales inmediatas que estudiarás más adelante. Es fácil
comprobar que las igualdades indicadas son válidas mediante la derivación, es decir, se
puede verificar que la derivada del segundo miembro es igual al integrando.
Las propiedades generales de las integrales indefinidas pueden también deducirse de
las propiedades homólogas de las derivadas.
1. La integral de una suma es igual a la suma de las integrales.
f ( x ) g( x )dx f ( x )dx g( x )dx .
2. La integral de una constante por una función es la constante por la integral de la
función.
k f ( x ) dx k f ( x ) dx .
3. La integral de una potencia es igual a la potencia más uno entre la potencia más
uno.
x n dx
x n 1
C , si n 1.
n 1
45
EXPLICACIÓN INTEGRADORA
46
RECAPITULACIÓN
47
ACTIVIDADES INTEGRALES
Realiza los siguientes ejercicios:
1. Sea la función y = x
4
a) Grafica la función.
b) Obtén la derivada
c) Grafica la función derivada
48
AUTOEVALUACIÓN
A continuación se presenta la solución de las actividades integrales, compara tus
respuestas y si tuviste alguna duda regresa al capítulo o bien consulta a tu asesor de
contenido.
49
50
C A P Í T U L O
2
TÉCNICAS DE INTEGRACIÓN
2.1 CAMBIO DE VARIABLE
2.2 INTEGRACIÓN POR PARTES
2.3 INTEGRACIÓN DE FUNCIONES RACIONALES
DESCOMPOSICIÓN EN FRACCIONES PARCIALES
POR
2.3.1 Denominador Formado por una Función Lineal
2.3.2 Denominador Formado por Factores Lineales de Primer Grado que no
se Repiten
2.3.3 Denominador Formado por Factores de Segundo Grado que no se
Repiten
51
52
P R O P Ó S I T O
Existe una gran variedad de integrales que se tiene que transformar a un patrón
establecido y de ésta forma resolverlas, para ello el contenido de este fascículo pretende
que al concluir su estudio:
¿QUÉ APRENDERÁS?
A conocer y aplicar las técnicas de
integración más sencillas.
¿CÓMO LO APRENDERÁS?
Mediante la aplicación de conocimientos
algebraicos, geométricos y analíticos.
¿PARA QUÉ TE VA A SERVIR?
Para evaluar integrales que no se
obtienen de forma común en los
problemas de Ingeniería, Física, Química,
Biología,
Economía,
Administración,
Finanzas y Computación entre otras áreas
del conocimiento.
53
54
CAPÍTULO 2
TÉCNICAS DE INTEGRACIÓN
La integración es un procedimiento esencialmente de ensayo que facilita el cálculo de
cada integral que se presente. Ésta debe compararse con las distintas integrales
elementales ordinarias; si coinciden plenamente con alguna de ellas se conoce el
resultado, pero si existen diferencias se deberá recurrir a las técnicas de integración.
Como muchas integrales indefinidas es imposible encontrarlas directamente, debemos
buscar la forma de arreglarlas o presentarlas a las que ya conocemos, con base en
procesos matemáticos que requieran la aplicación adecuada de las propiedades básicas
que forman la estructura de la Matemática.
Dos principios permiten ampliar el alcance de la integración:
Considerar que cada regla de integración es un patrón o modelo.
Las reglas de derivación pueden suministrar una pauta para el patrón o modelo.
Ejemplo: la integral de una potencia cuya base es x corresponde a
x n dx
donde n es un número real diferente de – 1, que es un patrón o modelo.
La integral
x
5
dx se asemeja al patrón, por lo tanto,
corresponder a una expresión diferente de x.
n
d
, donde
x n 1
C ,
n 1
puede
Si la base de la potencia es diferente de x podemos utilizar una nueva variable, u, para
expresar el integrando como una potencia de la nueva variable.
55
Ejemplo:
x 2
4
dx , que es similar al patrón
x
n dx
.
Expresamos la base x + 2 como una nueva variable u, tal que u = x + 2; observa que
4
du = dx, por lo tanto, (x + 2) dx =
expresión original en términos de x:
u
4 du
4
x 2 dx
. Después de integrar sustituimos u por la
56
x 25
5
C .
2.1 CAMBIO DE VARIABLE
Analizaremos varios ejemplos para comprender el cambio de variable:
Encontrar
2x
1 x 2 dx .
x
Para comparar con el modelo
n dx
se debe recordar que:
1 x 2 1 x 2
1/ 2
Ahora la expresión queda
2x1 x
2
vemos que se asemeja al patrón.
.
1/ 2 dx , o bien, 1 x 2 1/ 2 2x dx . De esta manera
2
Si consideramos u = 1 + x , du será du = 2x dx, pero el exponente es ½ porque
corresponde a la n del modelo.
Como 2x dx es parte de la expresión original, al cambiar la variable queda:
2x1 x
2
1/ 2 dx
u
1/ 2 du
Esta expresión puede integrarse como:
u
1/ 2 du
2
u3/2
C u3/2 C
3/2
3
Al regresar a la variable original llegamos a:
2x
Halla
1 x 2 dx
2
1 x 2 3 / 2 C 2
3
3
1 x 2 3
C
3 x 5 dx .
Primero expresa el radical como una potencia:
Compara con el modelo
x
n dx
.
57
3 x 5 ____________________________.
Si u = 3x + 5, el exponente es ½ y du = ___________________________________________.
Como du es el triple de dx, por lo tanto, dx será la tercera parte de du.
u
En consecuencia,
1/ 2
du 1
u 1/ 2 du ; y tienes _________________________________.
3
3
Simplificando y sustituyendo u por su equivalente la integral queda:
Encontrar
3 x 5dx
3x 8
5/3
2
3x 53 / 2 C 2
9
9
3x 53
C .
dx .
Esta integral se acerca al modelo: ________________________________________________.
¿Cuál sería el valor de u y du? ___________________________________________________.
¿Cuál sería la integral una vez hecho el cambio de variable? ________________________.
Al simplificar se obtiene: ________________________________________________________.
Al cambiar u por su equivalente se tiene
¿Cómo calcularías
cos
5
3x 8
5/3
dx __________________________.
x senx dx ? ____________________________________________.
Primero se debe encontrar la diferencial de u = cos x _______________________________.
Así, sen x dx = du y
cos
5
x senx dx u 5 du .
Ahora se tiene la integral adecuada al patrón establecido, por lo tanto: ________________.
Comprender el método implica ejecutarlo mentalmente, en caso contrario, seguir el
algoritmo u = cos x; n = 5; du = sen x dx, que forma parte de la expresión original.
58
De acuerdo con el patrón, se tiene
u
original:
cos
5
5 du
u6
C ; regresando a la variable
6
x senx dx = _____________________________________________________________.
El método de cambio de variable para integrales indefinidas es una herramienta valiosa
siempre que se reconozca que el integrando es de la forma
f ( x ) f ' ( x )dx
ó
f ( x ) k f ' ( x ) dx , donde k es un número real.
Reconocer esta forma de integración es directamente proporcional al número de
ejercicios resueltos. Haz los siguientes ejercicios considerando los ejemplos anteriores.
Encontrar
x
3
7 6 x 2 dx
3
7 6 x 2 x dx .
Observa que el integrando contiene a x dx.
Cambiar la expresión mediante un equivalente que no utilice el radical: _______________.
En esta expresión, u = _____________; n = _____________; du = _____________.
Aparece un factor diferente de 1 en el integrando, por lo tanto, hay que multiplicar por su
inversa para compensar. Con esto hemos encontrado la semejanza con el patrón.
Escribe la integral con el cambio de variable: ______________________________________.
Comparar con el patrón y realizarla _______________________________________________.
Al sustituir se tiene: ____________________________________________________________.
Al hacer operaciones, la integral queda:
x
3
7 6 x 2 dx
1
7 6x 2 4 / 3 C
16
59
Encontrar
2x 5dx
x 2 5x 7
.
2
Si u = x + 5x + 7; du = (2x + 5) dx, entonces:
du
u
1/ 2
u 1/ 2 du ,
que es la forma similar al patrón.
Al aplicar la fórmula y regresar a la variable original, el resultado debe ser:
2x 5dx
x 2 5x 7
2 x 2 5x 7 C .
El patrón es una integral elemental ordinaria; sin embargo, habrá casos en que después
de ensayar distintos mecanismos algebraicos será imposible valerse del cambio de
variable, porque la integral no corresponde a un patrón establecido, momento en que se
deben aplicar otras técnicas de integración.
El cambio de variable se da cuando nos encontramos con integrales similares a las
integrales elementales ordinarias como los que aparecen en el Apéndice, mas si se
está familiarizando con la técnica, el cambio de variable se puede hacer
mentalmente.
ACTIVIDAD DE REGULACIÓN
Resolver la integral
2x 3 dx , aplicando el método por cambio de variable.
60
EXPLICACIÓN INTEGRADORA
El método por cambio de variable consiste en identificar la variable “u”, para que a partir
de ésta, se obtenga la diferencial de u “du” y así asociar la integral
conocido.
61
u du a un patrón ya
2.2 INTEGRACIÓN POR PARTES
Para Leibniz, uno de los iniciadores del Cálculo, la derivada de un producto era el
producto de las derivadas, conclusión engañosa y con frecuencia mal utilizada por
quienes se inician en el estudio del Cálculo Integral. Lo correcto es la integración por
partes, basada en la fórmula de la diferencial de un producto de funciones.
d (uv) = u dv + v du.
Mediante la integración de ambos miembros de esta expresión tenemos:
d(uv ) u dv v du .
Como
d(uv ) uv C (comparar con la lista de integrales del Apéndice)
uv u dv v du C
Esta expresión la podemos representar como:
u dv uv v du C
que se conoce como integración por partes. Esta fórmula establece que hallar
u dv es
v du . Su utilidad radica en que, si la selección de u y dv son apropiadas, la
integración de v du se facilitará más que la de u dv. Es decir, el cálculo de u dv se
realiza en dos partes, una con dv y otra con v du .
determinar
La selección de dv debe ser tal que pueda obtenerse v por la integración directa.
La aplicación de la fórmula para la integración por partes comienza con una integración
seguida por una derivación como se muestra enseguida:
u dv uv v du C
Paso 1 integrar
Paso 2 obtener la diferencial
El último paso es evaluar
v du .
No existen normas generales para elegir de entre u y dv, pero sí se recomienda:
62
a)
Descomponer en factores de tal manera que dx sea siempre una parte de dv.
b)
dv debe tener una integración inmediata.
¿Cuándo podremos aplicar el método de integración por partes?
Se debe considerar que este método permite hacerlo para aquellos integrandos que
incluyan productos de funciones polinomiales con trigonometría o logaritmos.
Los siguientes ejercicios ayudarán a comprender esta técnica, y el tener a la mano una
tabla de integrales agilizará la búsqueda de un patrón (el apéndice contiene una lista de
integrales elementales ordinarias).
Evaluar
x sen x dx .
Primero se debe elegir u, dv, aunque debes tener presente que la integración es un
carácter de ensayo; si no se logra encontrar la integral, cambia la elección después de
analizar las recomendaciones sugeridas.
Elegir que factor se debe designar como dv y determinar si la integración es posible
mediante la lista de integrales elementales del Anexo. Como sen x dx tiene una integral
directa,
senx dx cos x C , elegimos:
dv = sen x dx
v = cos x dx
u=x
du = dx
Sustituyendo en la fórmula de integración por partes tenemos:
x senx dx x( cos x ) C ( cosx )dx .
1
Efectuando los productos:
x senx dx x cos x cosx dx C
1
por lo tanto,
x senx dx x cos x senx C .
; pero
cos x dx senx C
2
,
Así, C = C1 + C2.
Recuerda que al hacer una integración se obtiene una constante de integración. La
primera integración se realiza cuando obtenemos v a partir de dv.
63
Encontrar
x sec
2
x dx .
2
Se puede elegir dv = sec x dx , pues tiene la facultad de integrarse directamente, lo cual
se confirma al consultar el Apéndice; por lo tanto, v = _______, si u = x ; entonces
du = _______, mediante la fórmula de integración por partes.
u dv uv v du
Sustituyendo los resultados en la fórmula de integración por partes:
x sec
Al consultar el Anexo:
por consiguiente,
Encontrar
2
x dx x tan x C1 tan x dx
tan x dx lnsec x C
x sec
2
2
;
x dx x tan x ln sec x C
x cos x dx .
El resultado a que se debe llegar es:
x cos x dx x senx cos x C
Recuerda que C = C1 + C2.
Habrás realizado una elección correcta cuando llegues fácilmente a una solución, en
caso contrario, tu segunda integral, v du, es más complicada que la original, u dv.
En ocasiones, una integral particular requiere aplicaciones repetidas de la integración por
partes; por ejemplo:
64
Evaluar
x
2
e x dx .
x
La expresión que puede integrarse en forma directa es e dx, por lo tanto:
x
2
dv = e dx
x
v=e
u=x
du = 2xdx
u dv uv v du tenemos:
Sustituyendo en
x
2
e x dx x 2 e x e x 2x dx x 2 e x C1 2 e x x dx
e
Esta última integral,
x
x dx , comprende un producto y vuelve a integrarse por partes:
x
dv = e dx
x
v=e
u=x
du = dx
Sustituyendo:
e
x
x dx x e x e x dx , pero
e
x
dx e x , por lo tanto
e
x
x dx x e x e x C .
Reuniendo las integrales:
x
Evaluar
z
3
2
e x dx x 2 e x 2x e x e x x 2 e x 2 x e x 2 e x C
e z 2 dz .
3
Descomponiendo en factores a z tenemos:
z
2 z e z2
dz .
Seleccionando u y dv.
2
dv e z2 z dz
1 z2
v e C1
2
u=z
du = 2zdz
65
Aplicando la fórmula de integración por partes:
z
2
1
1
e z 2 z dz z 2 e z 2 e z 2 2z dz
2
2
1 z2
e tenemos:
2
Al realizar operaciones y factorizar
z
Evaluar
2
e z 2 z dz
1 z2 2
e z 1 C
2
x 3 dx
1 x 2
Descomponiendo en factores a x
3
x
2
1 x 2
1/ 2
x dx .
Seleccionando u y dv:
2
2
dv = (1 – x )1/2 x dx
2 1/2
v = (1 – x ) + C1
u=x
du = 2x dx
Aplicando la fórmula de integración por partes:
x 3 dx
1 x 2
x 2 1 x 2
1/ 2
1 x
2
1/ 2 2x dx .
Al realizar operaciones en la expresión tenemos:
x 3 dx
1 x 2
1 x 2 x 2 2
C.
3
66
Resumiendo:
u dv
u v v du
Fórmula para la integración por partes. Expresa la integral u dv en términos de otra
integral, v du. Es necesario la selección apropiada de u y dv para que la segunda
integral sea más fácil de integrar que la primera.
La práctica es la forma de adquirir seguridad en el manejo de la integración por partes.
Esta requiere determinación, paciencia, estrategia y sobre todo, mucho empeño.
ACTIVIDAD DE REGULACIÓN
Si aplicas el método de integración por partes, ¿Cuál es la función que obtienes al
resolver
xe
2x
dx ?
EXPLICACIÓN INTEGRADORA
La integración por partes es uno de los métodos más recurrentes cuando se tiene un
producto de funciones. La fórmula para éste método es:
u dv
u v v du
La utilidad de este método radica cuando se hace la elección correcta de “u” y “dv”.
67
2.3 INTEGRACIÓN
DE
FUNCIONES
RACIONALES
DESCOMPOSICIÓN EN FRACCIONES PARCIALES
POR
Gran cantidad de problemas de Física, Química o de Matemáticas se pueden
representar con expresiones que contienen integrales de funciones racionales, cuya
notación general es:
P ( x ) dx
,
Q( x )
Que no pueden calcularse mediante los métodos conocidos. El procedimiento a seguir
es descomponer la función racional en fracciones parciales.
P( x )
. Esta función
Q( x )
puede ser propia si el grado del numerador, P(x), es menor que el grado de
denominador, Q(x); en caso contrario, se llama impropia. En ésta el numerador puede
representarse como la suma de un polinomio más una función racional propia.
Recuerda que la función racional es el cociente de dos polinomios,
La integración del polinomio no representa dificultad alguna, lo difícil es hallar las
primitivas de funciones racionales propias, las cuales pueden expresarse mediante
funciones racionales, trigonométricas, exponenciales o sus inversas.
La mayoría de las integrales racionales pueden reducirse a la forma d
integral corresponde a un logaritmo natural.
/
, cuya
Los ejemplos que estudiaremos son de los casos más representativos.
2.3.1 DENOMINADOR FORMADO POR UNA FUNCIÓN LINEAL
Encontrar
x
x 1 dx
Efectuaremos la división hasta que el grado del residuo sea menor que el denominador:
x
1
1
x 1
x 1
Por lo tanto:
x
1
dx
x 1 dx 1 x 1dx dx x 1 .
68
Usando las fórmulas del Anexo para calcular las integrales obtenemos:
x
x 1 dx
x ln x 1 C
Calcular las integrales b) y c) con base en a).
a)
Hallar
x2
x 3 dx .
2
Divide x entre x – 3:
x3
9
x 3
La integral se descompone en:
9
x 3dx x 3 dx
La primera integral es directa y no tiene dificultad.
x 3dx
x2
3 x C1
2
La segunda,
9
x 3 dx ,
Se acerca al patrón
dv
v
y vemos que puede calcularse como
9
dx
x 3
9 ln x 3 C 2
En consecuencia:
x2
x2
dx
3 x 9 ln x 3 C ,
x 3
2
donde: C = C1 + C2 .
69
b)
Calcular
x
x 2 dx .
¿Cuál es el primer paso para calcular la integral? __________________________________.
¿Cuál es el resultado de la división? ______________________________________________.
¿Cómo se descompone la integral? ______________________________________________.
¿Cuál es el resultado de la primera integral? ______________________________________.
¿Cómo se resuelve la segunda integral? __________________________________________.
Escribe el resultado de
¿Coincide con
c)
x
x 2 dx _______________________________________________.
x
x 2 dx x 2 ln x 2 C ? ____________________________________.
Encontrar
x2
x 5 dx .
¿El resultado de la división es? __________________________________________________.
La integral se expresa como: ____________________________________________________.
Completando el algoritmo obtienes:
x2
x2
5x 25 ln x 5 C
dx
x5
2
Con fracciones racionales más complejas se deberá reducir a una expresión mixta
mediante la división. Para integrarla se descompone en fracciones parciales más
simples, lo cual es posible siempre que el denominador pueda integrarse en factores
primos.
Hay diferentes formas para descomponer los factores del denominador, mas en este
fascículo sólo estudiaremos dos.
70
2.3.2 DENOMINADOR FORMADO POR FACTORES LINEALES DE PRIMER GRADO
QUE NO SE REPITEN
Encontrar
2x 3 dx
x
3
x 2 2x
.
3
2
Como 2x + 3 no es la derivada de x + x – 2x, debemos recurrir a este método.
Consideramos el integrando, del cual factorizamos su denominador (recuerda los
métodos de factorización estudiados en primer semestre); en este caso x es factor de los
tres términos del denominador, por consiguiente, podemos expresar el denominador
2
2
como x (x + x – 2) y, a su vez, x + x – 2 se factoriza como (x + 2) (x – 1), en
consecuencia, la factorización es x (x + 2) (x – 1). Observamos que los factores son
lineales y no se repiten.
A continuación se descompone la función racional en una suma de otras más simples.
Se debe tener en cuenta que a cada factor no repetido de primer grado corresponde una
A
fracción parcial de la forma
, siendo A una constante diferente de cero, y x – a
x a
factor denominador. Para comprobar la igualdad se debe considerar el número de
factores encontrados en el denominador, el cual tiene que corresponder al número de
constantes que debemos conocer.
2x 3
A
B
C
x x 1x 2
x x 1 x 2
El método más breve para obtener los valores de A, B y C es el siguiente:
Multiplicamos la igualdad (1) por x (x – 1) (x + 2), producto que suponemos diferente de
cero. Simplificando queda:
2x + 3 = A(x – 1) (x + 2) + B(x + 2)x + C(x – 1)x
2
2
2
2x + 3 = A(x + x – 2) + B(x + 2x) + C(x – x).
Puesto que esta ecuación es una identidad, al factorizar el segundo término de la
expresión igualamos los coeficientes correspondientes a las mismas potencias de x en
los dos miembros y obtenemos tres ecuaciones que se pueden resolver por
determinantes.
Agrupando el segundo término de la expresión tenemos:
2
2x + 3 = (A + B + C)x + (A + 2B – C)x – 2A .
71
Igualando los coeficientes:
A+B+C =0
A + 2B – C = 2
2A = 3
Resolviendo el sistema obtenemos:
A
3
5
1
, B
y C .
2
3
6
Con estos valores nuestra expresión resultante es:
2x 3
3
5
1
x x 1x 2
2x 3x 1 6x 2
Verificar la igualdad mediante la suma de fracciones para comprobar si los valores de A,
B y C son correctos. La integral se descompone en una suma de tres integrales que
calculamos con base en el Anexo.
2x 3
xx 1x 2 dx
Evaluar
x 2 dx
x2 1
3 dx
5
2 x
3
dx
x 1
1
6
dx
x2
3
5
1
ln x ln x 1 ln x 2 C
2
3
6
.
Los factores del denominador son (x + 1) (x – 1), y el integrando es:
x 2 dx
x 1x 1 .
El número de constantes a determinar es equivalente al número de factores encontrados
en el denominador del integrando. En este caso son dos (A, B). Quitando el símbolo de
integración iniciamos el método empleado en el ejemplo anterior.
El integrando se descompone en:
x 2
x 1x 1
72
A
B
x 1 x 1
Al obtener los valores de A y B, se tiene que A
3
1
y B .
2
2
Sustituyendo los valores de A y B en la expresión del integrando, tenemos:
x 2
x 1x 1
3
1
2x 1 2x 1
Tras comprobar la igualdad podemos integrar:
x 2 dx
x 1x 1
Calcular:
x
4x 2 dx
3
3
2
3 x 2 2x
dx
1
dx
x 1 2 x 1
3
1
ln x 1
ln x 1 C
2
2
.
1. Considera el integrando como una función racional. El denominador es de grado
3; por lo tanto, al factorizarlo se tienen tres factores y se deben determinar tres
constantes.
2. Factorizar el denominador _______________________________________________.
3. Con el denominador factorizado igualar la función racional con las constantes
por determinar. Escribir la igualdad ________________________________________.
4. Efectuar la suma de la parte derecha de la igualdad, eliminar denominadores,
hacer operaciones y simplificar. Anota los resultados ________________________.
5. Con base en el ejemplo anterior, considerar la ecuación como una identidad y
encontrar el sistema correspondiente ______________________________________.
6. Resolver el sistema y encontrar los valores de:
A =______
B = ______
C = ______
Anotar los valores obtenidos en la expresión:
4x 2
x 3 3 x 2 2x
x
x 2 x 1
73
Ahora ya se puede integrar:
x
4x 2 dx
3
3 x 2 2x
dx
x
3dx
2dx
x 2 x 1
dx
dx
dx
.
3
2
x
x2
x 1
El resultado es:
x
Calcular
x
4x 2 dx
3
x 1 dx
3
ln x 3 ln x 2 2 ln x 1 C
3 x 2 2x
.
x 2 2x
Anotar la función racional sin la integral _______________________________________.
Factorizar el denominador ______________________________________ y determinar
las constantes necesarias. Recuerda que el número de constantes por determinar es
igual al grado del denominador que a su vez corresponde al número de factores por
encontrar.
¿Cuántas constantes se deben determinar? ___________________________________.
Determinar la igualdad con las constantes necesarias: eliminar denominadores. La
expresión es: _______________________________________________________________
___________________________________________________________________________.
Encontrar el sistema que permita encontrar los valores de:
A =______
B = ______
C = ______
Sustituir estos valores en la identidad e integrar.
¿Qué expresión se debe integrar? ____________________________________________.
El resultado es:
x
x 1 dx
3
x 2 2x
1
1
2
ln x ln x 2 ln x 1 C
2
6
3
74
2.3.3 DENOMINADOR FORMADO POR FACTORES DE SEGUNDO GRADO QUE NO
SE REPITEN.
Hasta ahora hemos visto integraciones donde el denominador de la función racional se
descompone en factores lineales que no se repiten. Teóricamente, es posible escribir
cualquier expresión racional:
P( x )
Q( x )
Como una suma de expresiones racionales cuyos denominadores son polinomios de
grado no mayor que dos.
Si P(x) y Q(x) son polinomios y el grado de P(x) es menor o igual que el de Q(x),
entonces se sigue el teorema de Álgebra que se expresa como:
P( x )
F1 F2 ... Fk ,
Q( x )
donde cada F1 corresponde a una fracción parcial que tiene una de las dos formas
siguientes:
A
Cx D
ó
ax b
ax 2 b c
donde A, B y C son constantes no simultáneamente nulas.
La integración de estas fracciones es similar a la realizada. Para comprenderlo
desarrollemos un ejemplo:
Evaluar
x
4 dx
4x
3
3
2
El denominador, x + 4x, se puede factorizar encontrando su factor común, x (x + 4), por
lo tanto:
4 dx
es nuestra integral
x x 2 4
Al aplicar el algoritmo a la expresión
4
x x 2 4
A Bx C
x x2 4
y quitando denominadores queda:
2
4 = A(x + 4) + (Bx + C) x.
75
Se efectúan operaciones:
2
2
4 = Ax + 4A + Bx + Cx
Se agrupan términos semejantes:
2
4 = (A + B)x + Cx + 4A.
Igualamos los coeficientes de las mismas potencias de x y tenemos:
A+B=0
C=0
4A = 4;
Por lo tanto, A = 1. Sustituyendo en A + B = 0, queda 1 + B = 0; B = 1 y C = 0, de
manera que:
4
x
1
x
2
x x 4
4
dx
x
x
x2
Integramos:
4 dx
2 4
xx
x dx
ln x
2 4
x dx
2 4
x
Esta segunda integral se puede resolver mediante cambio de variable.
x
Encontrar
4 dx
1
ln x ln x 2 4 C
2
4x
3
x2 x 1
dx .
2 1
2x 1x
Para trabajar con la función racional primero se elimina la integral.
x2 x 1
A
Bx C
2x 1x 2 1 2x 1 x 2 1
Con base en los ejemplos anteriores anotar los pasos a seguir para llegar a la siguiente
expresión:
2
2
x + x + 1 = (A + 2B)x + (B + 2C)x + (A + C).
76
Estos dos polinomios son idénticos si las potencias de x tiene los mismos coeficientes,
es decir:
A + 2B = 1
B + 2C = 1
A + C = 1.
Estas tres ecuaciones se resuelven por determinantes. Los valores son:
3
1
2
, B
,C
.
5
5
5
A
La fracción queda expresada como:
x2 x 1
1 3
x2
2
2
2x 1 x 1 5 2x 1 x 1
Al integrar:
x2 x 1
1 3 dx
x dx
2 dx
dx
2
2
.
2
5
2
x
1
x 1
x 1
1
2x 1x
Las dos primeras integrales se resuelven por cambio de variables y la tercera se
compara con la lista de integrales del Anexo:
Primera integral:
3 dx
2x 1
u = 2x + 1; du = 2dx y
por lo tanto,
Segunda integral:
du
dx ;
2
dx
3
1 du
1
ln 2x 1 C1
lnu ; 3
2x 1
2
2 u
2
x dx
;
2
1
x
2
hacemos u = x + 1
du = 2x dx
du
x dx .
2
Al sustituir
1 du
1
lnu , se obtiene:
2 u
2
77
x dx
1
ln x 2 1 C 2 .
2
2
1
x
x
La tercera integral:
2
2
1
dx
Se compara con la lista de integrales elementales del Anexo.
v
2
v
dv
1
tan1 C
2
a
a
a
x
2
dx 2 tan1 x C 3 .
1
2
Regresando a las variables originales tenemos:
x2 x 1
1 3
1
2
1
2x 1 x 2 1 dx 5 2 ln2x 1 2 ln x 1 2 tan x C
Donde: C = C1 + C2 + C3 .
Al multiplicar los coeficientes la expresión final es
3
1
2
ln 2x 1
ln x 2 1 tan1 x C
10
10
5
Con base en este procedimiento haz el siguiente ejemplo:
Evaluar
x 4 dx
3
x 4x
x 4 dx
x x
2
4
Eliminar la integral para empezar el algoritmo y señalar las constantes por determinar.
Recuerda que el número de constantes corresponde al grado de denominador y éste es
el exponente máximo del denominador; por consiguiente,
x4
A Bx C
.
2
x x2 4
x x 4
Para que exista la identidad, los coeficientes de ambos términos de la igualdad deben
2
coincidir; así, A + B = 0, pues no existe x ; C = 1 que es el coeficiente de x y 4 = 4A. De
acuerdo con estos valores: A_______, B_______, C_______.
Al sustituir estos valores e integrar la expresión:
x 4 dx
x x
2
4
dx
x
x
78
dx
2
4
x dx
x
2
4
.
Cada una de estas integrales se acomoda a los patrones ya estudiados en este
fascículo.
El resultado es:
x 4 dx
x x
2
4
ln x
1
1
x
ln x 2 4 tan1 C .
2
2
2
Listar los pasos a seguir para este tipo de integración y resolver las siguientes integrales:
a)
4x 2 3x 1
x 2 x 1 dx
b)
2x 11 dx
x 2 x 1
Los resultados que debes obtener son:
a) 6 ln x 1 2 ln x
b)
9 ln x 9 ln x 1
1
C.
x
11
C.
x
La integración de funciones racionales por fracciones racionales requiere un
procedimiento basado en los algoritmos de la división de polinomios y de los
distintos tipos de factorización estudiados en Matemáticas I.
En los dos últimos casos presentados, factores lineales sin repetición y factores
cuadráticos sin repetición, los procedimientos de solución son similares.
79
ACTIVIDAD DE REGULACIÓN
Integrar 2
x2
dx .
x 1
EXPLICACIÓN INTEGRADORA
Una integral de una función racional se expresa:
P( x )
Q( x ) dx .
Donde P(x) y Q(x) son funciones polinomiales.
– Si el grado de P(x) es menor que el grado de Q(x), se llama integral propia y el método
P( x )
de integración consiste en escribir
como la suma de fracciones parciales.
Q( x )
– Si el grado de P(x) es mayor que el grado de Q(x), se llama integral impropia. En este
caso se divide el numerador entre el denominador hasta que so obtenga una integral
propia, para así resolver la integral como propia.
80
RECAPITULACIÓN
81
ACTIVIDADES INTEGRALES
Coloca los números 1, 2, 3 en los paréntesis según la técnica de integración adecuada
para resolver la integral.
x
a) (
)
b) (
)
2x
c) (
)
3 cos 3x
x 1
3
dx
1. Cambio de variable.
7
1 x 2 dx
2. Integración por partes.
3. Fracciones parciales
dx
82
AUTOEVALUACIÓN
A continuación se presenta la solución de las actividades integrales, compara tus
respuestas y si tuviste alguna duda regresa al capítulo o bien consulta a tu asesor de
contenido.
a) (2)
b) (1)
c) (1)
83
A N E X O
Fórmulas de integración de formas elementales ordinarias
1.
du dv dw du dv dw
2.
adv a dv
3.
dv v C
4.
v n dv
5.
dv
lnv C
v
6.
a v dv
7.
e
8.
senv dv cosv C
9.
cosv dv senv C
10.
sec
2
v dv tanv C
11.
csc
2
v dv cot v C
v
v n 1
C
n 1
av
C
ln a
dv e v C
84
a 2 v 2 dv
v
a2
a
a2 v 2
sen 1 C
2
2
v
13.
v 2 a 2 dv
v
a2
v 2 a2
ln v v 2 v 2 C
2
2
14.
v
2
15.
a
2
16.
sec v tanv dv sec v C
17.
csc v cotv dv csc v C
18.
tanv dv lncosv C
19.
cot v dv lnsenv C
20.
sec v dv lnsec v tanv C
21.
csc v dv lncsc v cot v C
22.
v
23.
24.
25.
v
12.
2
dv
1 v a
ln
C
2
2a v a
a
v
2
a2
dv
1 av
ln
C
2a a v
v2
v
2
a2
ó
tanv dv lnsec v C
v
dv
1
tan1 C
a
a
a2
dv
2
a v
sen 1
2
dv
v a2
dv
v a
ln v v 2 a 2 C
2
2
v
C
a
2
v
1
sec 1 C
a
a
85
86
C A P Í T U L O
3
APLICACIONES DEL CÁLCULO INTEGRAL
3.1 VALOR PROMEDIO DE UNA FUNCIÓN Y ÁREA BAJO LA
CURVA
3.2 INTEGRAL DE LA RAZÓN DE CAMBIO INSTANTÁNEA
3.3 ÁREA BAJO LA CURVA
3.4 ÁREA ENTRE CURVAS: UTILIDADES
3.5 CÁLCULO E INTERPRETACIÓN DE LA CONSTANTE DE
INTEGRACIÓN
87
88
P R O P Ó S I T O
El contenido de este fascículo pretende que al concluir su estudio:
¿QUÉ APRENDERÁS?
A aplicar los conocimientos tanto de la
integral indefinida como de la definida.
¿CÓMO LO APRENDERÁS?
Mediante la utilización de algunas técnicas
de integración en la resolución de
diferentes problemas de aplicación real
generados por fenómenos dinámicos.
¿PARA QUÉ TE VA A SERVIR?
Para mayor comprensión del cálculo
integral y su aplicación en las diferentes
ramas de la Ciencia.
89
90
CAPÍTULO 3
APLICACIONES DEL CÁLCULO INTEGRAL
Analiza las siguientes preguntas.
¿Sabías que existe un método para evaluar la temperatura
en lugares extremadamente fríos?
¿Cómo se puede saber la cantidad dosificada de insulina
para un diabético en diferentes periodos?
¿Cómo calcularías la energía que consume un sistema de clima artificial?
¿Sabías que se puede pronosticar el número total de bacterias de cierto cultivo
para un instante determinado?
El estudio de este fascículo te permitirá conocer las diversas aplicaciones que tiene el
Cálculo Integral y además, contestar estas interrogantes y muchas otras de la misma
índole que se puedan presentar.
91
3.1 VALOR PROMEDIO DE UNA FUNCIÓN Y ÁREA BAJO LA CURVA
En el Polo Norte se registra semanalmente la temperatura del ambiente al mediodía,
durante un año. Las lecturas obtenidas fueron las siguientes:
Semana
Núm.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Temperatura
T(°C)
3.4
6.7
9.8
12.7
15.3
17.7
19.7
21.5
23.0
24.2
25.0
25.5
25.7
25.5
25.0
24.2
23.0
21.5
19.7
17.7
15.3
12.7
9.8
6.7
3.4
0.0
Semana
Núm.
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
92
Temperatura
T(°C)
3.6
7.3
11.0
14.8
18.6
22.3
25.9
29.4
32.7
35.7
38.5
40.9
42.8
44.9
45.3
45.7
45.4
44.4
42.5
39.7
36.0
31.3
25.4
18.2
9.8
0.0
La gráfica de barras para las primeras 26 semanas es:
Figura 1.
La gráfica de barras para las siguientes 26 semanas es:
Figura 2.
93
¿Cómo obtendrías la temperatura promedio durante las primeras 26 semanas?
Es como si en lugar de tener 26 barras de alturas diferentes (Figura 1) tuvieras
solamente una, de altura constante (Figura 3).
Figura 3.
Ésta no es tan alta como la barra más alta (13) ni tan baja como la más baja (26). Esto
se debe a que las barras altas ceden pequeñas porciones a las barras pequeñas, de
modo que la altura entre todas se iguala. Esto es, se está obteniendo el promedio de la
altura de las 26 barras. Además, el área que representan las 26 barras debe ser igual a
la que representa la barra única de 26 semanas de ancho.
Para obtener el promedio de un número dado de datos deben sumarse todos ellos y
posteriormente dividirse entre el número de datos. Así, la suma de la altura de las barras
es 434.7°C, y al dividir este valor entre el número de datos (26) se obtiene el promedio
de temperatura durante las primeras 26 semanas, es decir:
434.7
16.72 ºC
26
Para calcular el área de la barra ancha, de altura cuyo valor es 16.72°C, se multiplica la
longitud de la base (26) por la altura (16.72); por consiguiente, el área es de
434.7°C x semana.
Figura 4.
94
Si se desea determinar la prueba hay que calcular la suma de las áreas de las 26
primeras barras multiplicando la altura de cada barra por la longitud de la base, cuyo
valor en este problema siempre es de 1; por último se efectúa la suma de áreas. El
resultado que se obtiene es de 434.7°C x semana.
Es el mismo procedimiento para calcular la temperatura promedio de las siguientes 26
semanas. Su promedio es de – 28.91°C(figura 5).
Figura 5.
Para calcular el área se multiplica –28.91 por 26; por lo tanto, el área es de 751.6 [°C x
semana], mismo resultado que la suma de las áreas de las 26 barras consideradas.
La temperatura promedio de las 52 semanas se obtiene mediante la suma de las dos
áreas, que se divide entre el número de semanas como sigue:
434.7 ( 751.6)
º C x semana
6.1 º C
semana
52
Con la relación funcional entre la temperatura y el tiempo transcurrido se determinan los
fenómenos en estudio y se predicen futuros comportamientos; sin embargo, las más
veces es complicado porque es necesario aplicar diversos conocimientos sobre
funciones y comparar muchas de ellas hasta obtener la que mejor se ajuste a los datos
registrados.
La función o modelo matemático, cuya gráfica pase por los 52 puntos de la figura 6,
aunque sea cercanamente, tiene la forma siguiente:
95
Figura 6.
Después de probar diversas funciones, la que mejor se ajusta a ella es:
4
2
ƒ(t) = 0.0001(t – 13) – 0.169(t – 13) + 25.7,
Donde t es el número de semanas, el cual queda comprendido en el intervalo 0 t 52,
y ƒ(t) expresa la temperatura en grados Celsius (°C).
Para comprender qué significa la integral definida de la función ƒ(t) veamos un ejemplo:
52
0
f (t ) dt
Al calcular la función:
52
0
f (t ) dt
52
0
0.0001t 13
4
0.169t 13 25.7 dt
2
0.0001t 135 0.169t 133
f (t ) dt
25.7t
0
5
3
52
0
0
0
f (t ) dt 0.00002t 13 0.05633t 13 25.7t
52
52
5
3
f (t ) dt 316.886 º C x semana
52
96
52
0
Este valor es el mismo que se obtiene al sumar las áreas de las 52 barras, o cuando se
suman las áreas de las dos barras anchas; por consiguiente:
434.7 + (751.6) = 316.886 °C x semana
La integral definida es el área bajo la curva o bien el total acumulado de las temperaturas
si el tiempo transcurrido entre una y otra lectura es de una semana.
Definición
El área bajo la curva ƒ(t), desde que t forma el valor de a hasta que t toma el valor de
b, es la siguiente integral definida:
A
b
a
f (t ) dt
La figura ilustra los límites de integración,
f(t)
A
a
b
t
ba
donde b – a es la longitud de la base.
Para obtener la temperatura promedio de las 52 semanas se divide el área bajo la curva
o el total acumulado de temperaturas entre el número de semanas o entre la longitud de
la base del área considerada, b – a, o sea, 52 – 0.
Así:
Temperatura promedio anual
316.88 º C x semana
semana .
52
Las semanas pueden cancelarse y únicamente queda °C.
Temperatura promedio anual = 6.1°C, que es el mismo valor calculado por medio de los
diagramas de barras.
97
En conclusión, el valor promedio de una función, f , se define matemáticamente como:
f
Donde
1
ba
b
a
f (t ) dt
b
a
f (t ) dt es la suma total de valores o el área bajo la curva, y b – a la longitud de
la base del área considerada.
Dado que la función ƒ(t) es sólo una aproximación a la gráfica que se obtuvo con el
registro de datos, el área bajo la curva calculada por medio de la integral definida podría
tener un valor diferente que el calculado mediante las barras. Lo mismo puede suceder
al calcular el valor promedio de la función, puesto que únicamente se divide el valor de la
integral definida entre la longitud del intervalo.
ACTIVIDAD DE REGULACIÓN
Analiza la siguiente tabla.
t
G(t)
0
80
1
83.38
2
88.25
3
91.97
4
92.96
5
92.25
En la tabla anterior, G(t) indica el ingreso nacional bruto en mmd de la compañía
Anadac y t es el tiempo en años desde la fecha de su pronóstico.
¿Puedes decir cuál es el promedio de los datos representados?
98
EXPLICACIÓN INTEGRADORA
El valor promedio de una serie de datos se obtiene sumando todos ellos y después se
dividen entre el número de datos. Así, de acuerdo al ejemplo presentado en este
apartado, se tiene que la temperatura promedio en el Polo Norte, es:
T
3.4 6.7 9.8 .... ( 18.2) ( 9.8)
6.1C
52
Que es el mismo valor que se obtiene al emplear la fórmula del valor promedio de una
función:
f
1
ba
f
1
52
b
a
f (t ) dt
0.0001(t 13)
52
0
4
0.169(t 13) 2 25.7 dt
f 6.1C
99
3.2 INTEGRAL DE LA RAZÓN DE CAMBIO INSTANTÁNEA
Para controlar el organismo de un diabético existe la implantación de una cápsula que
proporciona insulina, lenta y continuamente, a la corriente sanguínea. Al medir la
cantidad de insulina administrada al paciente se registró lo siguiente:
tiempo
(días)
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Dosis acumulada
3
(cm )
0.00
0.10
0.36
0.78
1.33
1.99
2.73
3.56
4.45
5.38
6.36
7.37
8.39
9.44
10.49
11.54
12.58
13.62
14.65
15.66
16.66
17.64
18.59
19.52
20.43
21.31
22.17
23.00
23.80
24.57
25.32
tiempo
(días)
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
100
Dosis acumulada
3
(cm )
26.04
26.74
27.41
28.05
28.66
29.26
29.82
30.37
30.89
31.38
31.86
32.31
32.75
33.16
33.55
33.93
34.29
34.63
34.96
35.27
35.56
35.84
36.11
36.36
36.60
36.83
37.05
37.25
37.44
37.62
Para hallar la razón de cambio promedio (RCP) entre dos puntos, A y B, se divide el
incremento de la función, ƒ(b) – ƒ(a), entre el incremento de la variable independiente, b
– a.
f ( b ) f (a )
RCP
ba
Donde: ƒ(a) – ƒ(b) son los valores de la función evaluada en t = a y t = b,
respectivamente. La figura 7 ayuda a recordar este concepto.
Figura 7.
La razón de cambio promedio entre t = 0 y t = 1 se obtiene como sigue:
RCP1
f (1) f (0)
;
1 0
Como ƒ(1) = 0.1 y ƒ(0) = 0 ; entonces RCP1
101
0.1 0 cm 3
1 0 dìa
cm 3
RCP1 0.1
dìa
ACTIVIDAD DE REGULACIÓN
Determinar los datos que faltan en la siguiente tabla.
3
Intervalo
1
2
3
4
5
6
ba
1
1
1
1
1
ƒ(b) – ƒ(a)
0.10
0.26
0.42
0.55
RCP cm /día
0.10
0.26
0.42
0.55
60
1
0.18
0.18
La gráfica de barras de la razón de cambio promedio, tiene la siguiente forma:
Figura 8.
102
La suma de las áreas de todas las barras se obtiene al multiplicar a la altura de cada
barra RCP por la longitud de la base, que en este caso es de un día; posteriormente se
suman todos los productos:
RCP
1
1 60
Donde:
RCP
160
1
3
37.6 cm de insulina,
es la suma de las áreas de todos los rectángulos, desde el 1. hasta el
60. día.
Esta suma representa el total de insulina suministrada al paciente al 60. día.
Encontrar el área de todos los rectángulos comprendidos desde el inicio del suministro
de insulina hasta el 30. día. Se puede hacer de tres maneras:
RCP
Primera
130
1
Encontrar la suma de las áreas de todos los rectángulos hasta el 30. día. El valor por
buscar es:
RCP1 25.32
130
Donde,
significa suma y
cm 3
dìa
suma de las áreas de todos los rectángulos
130
comprendidos desde el inicio del tratamiento, que corresponde al 1. rectángulo, hasta el
día 30, que corresponde al 30. rectángulo.
Segunda
El mismo valor del área se puede encontrar al sumar las siguientes áreas parciales.
RCP
1
130
RCP RCP
1
1130
RCP
130
o bien,
1
1
110
18.96 6.36
RCP1 25.32
130
103
cm 3
de insulina.
día
Tercera
Encontraremos el mismo valor del área con la suma de áreas parciales.
RCP
RCP
8.66 16.66
1
130
1
130
RCP RCP
1
2130
1 20
1
o bien,
RCP1 25.32
130
cm 3
de insulina.
día
Como hay gran cantidad de combinaciones con las que obtendrías el mismo resultado,
se puede verificar que
RCP
1 b
Donde:
RCP
130
1
1
RCP RCP
( a 1) b
1
1 a
1
es el total de insulina suministrada al paciente, desde el 1. hasta el
30. día.
La figura 9 representa los valores de la razón de cambio promedio encontrados.
Figura 9.
104
Encontrar la función que pase, aunque sea cerca, por todos los puntos de la gráfica es
bastante laborioso, aunque la que más se aproxima a la gráfica anterior es:
ƒ(t) = 0.2te
–0.07t
3
cm /día,
que representa la función de cambio instantáneo, ƒ(t), con la que se suministra la
insulina en términos de tiempo, t.
La gráfica de la función de la razón de cambio instantáneo es continua, y puede
obtenerse al unir todos los puntos de la gráfica de la razón de cambio promedio (figura
10).
Figura 10.
Recuerda que el área bajo la curva puede calcularse por medio de una integral definida
de la función en cuestión, que para este caso representa la función de la razón de
cambio instantáneo. Por lo tanto, para calcular el total de insulina suministrada desde
que inicia el tratamiento hasta el 60. día se debe evaluar la integral definida de la
función de la razón de cambio instantáneo.
Cantidad total
0 60
60
0
0.2te 0.07 t dt
Utilicemos el método de integración por partes para evaluar la integral definida.
La fórmula es:
udv uv vdu,
105
y como:
0 60
Se escoge: u = t y dv = e
entonces,
Cantidad total 0.2
du = dt y
-0.07t
60
0
te 0.07 t dt
dt ;
dv .
Al aplicar la fórmula de integración por partes resulta:
60
1
1
Cantidad total = 0.2t
e 0 07 t
e 0.07 t dt ,
0 60
0.07
0
0.07
o
60
t
1
e 0.07 t
e 0 07 t dt ,
Cantidad total = 0.2
0
.
07
0
.
07
0 60
0
o bien,
60
t
1
e 0.07 t
e 0 07 t 0.07dt ,
Cantidad total = 0.2
0.07
0.07
0
0 60
o también
60
t
1
Cantidad total = 0.2
e 0.07 t
e 0.07 t ,
2
0.07
0.07
0
0 60
Al sustituir los límites de integración resulta:
60 0.07 ( 60 )
0
1
1
0.07 ( 60 )
0.07 ( 0 )
0 07 ( 0 )
Cantidad total = 0.2
e
e
e
e
.
0.072
0.072
0.07
0 60
0.07
Al efectuar los productos indicados queda:
Cantidad total = 0.2 12.853 3.06 0 204.0816 ,
0 60
106
o bien,
Cantidad total = 0.2 [188.168],
0 60
o también
3
Cantidad total = 37.634 cm de insulina suministrados durante los primeros 60 días.
0 60
Como se puede encontrar una equivalencia aproximada entre la suma de las áreas y la
integral definida, por consiguiente:
RCP
1 60
1
60
0
(función de la razón de cambio instantáneo) dt .
Ahora calcularemos el total de insulina suministrada hasta el 30. día con base en
integrales definidas.
Primera
Encontramos el total de insulina suministrada hasta el 30. día.
Cantidad total =
0 30
30
0
(función de la razón de cambio instantáneo) dt .
Al sustituir la función queda:
Cantidad total =
0 30
30
0
0.2te 0.07 t dt .
Esta integración se realizó para evaluar el total de insulina suministrada hasta el 60º. día
con la excepción de que los límites de integración son diferentes. Así:
30
t
1
e 0.07 t
e 0.07 t ,
Cantidad total = 0.2
2
0.07
0.07
0
0 30
o
30 0.07 (30 )
1
0 0.07 ( 0 )
1
Cantidad total = 0.2
e
e 0.07 ( 30 )
e
e 0 07 ( 0 ) ,
2
2
0.07
0.07
0.07
0 30
0.07
107
o bien,
Cantidad total = 0.2 52.4813 24.9911 0 204.0816 ,
0 30
o también,
Cantidad total = 0.2 [126.6092],
0 30
3
Cantidad total = 25.32 cm de insulina suministrado durante los primeros 30 días.
0 30
Este valor también lo calculamos al sumar las áreas de todos los rectángulos hasta el
30. día.
También aquí puedes encontrar la equivalencia aproximada entre la sumas de las áreas
y la integral definida; por consiguiente,
RCP
1 30
1
30
0
(función de la razón de cambio instantáneo) dt .
Segunda
La misma cantidad de insulina se puede encontrar al sumar las siguientes cantidades:
Cantidad total =
0 30
30
10
10
0
(función de la razón de cambio instantáneo) dt +
(función de la razón de cambio instantáneo) dt .
Al sustituir la función de la razón de cambio instantáneo tenemos:
Cantidad total =
0 30
30
10
0.2te 0.07 t dt +
10
0
0.2te 0.07 t dt
Al evaluar las integrales se obtiene
Cantidad total = 18.962 + 6.359.
0 30
3
Cantidad total = 25.321 cm de insulina suministrados durante los primeros 30 días.
0 30
108
La equivalencia aproximada entre la suma de las áreas y la integral definida es:
RCP
1 30
1
30
10
(función de la razón de cambio instantáneo) dt +
10
(función de la razón de cambio instantáneo) dt .
0
donde la expresión
10
0
(función de la razón de cambio instantáneo) dt representa la
insulina suministrada al paciente hasta el 10. día, de ahí que se pueda utilizar la
siguiente equivalencia:
10
0
(función de la razón de cambio instantáneo) dt = Acum10.
El valor aproximado de esta integral lo puedes encontrar en tu registro de datos para el
10. día. Entonces, la equivalencia aproximada entre la suma de las áreas de la integral
definida se determina como:
RCP
1 30
1
30
10
f (t )dt Acum10
,
donde:
ƒ(t) representa la función de la razón de cambio instantáneo.
Acum10 representa el valor acumulado de insulina hasta el 10. día.
Tercera
Encontramos la misma cantidad de insulina con la suma siguiente:
Cantidad total =
0 30
30
20
20
f (t )dt f (t )dt
0
Recuerda que ƒ(t) es la función de la razón de cambio instantáneo. Además, como el
valor de la integral
20
0
f (t )dt
representa la cantidad acumulada de insulina hasta el 20. día, entonces,
Cantidad total =
0 30
30
20
f (t )dt Acum20 .
109
Al evaluar las integrales se obtiene
Cantidad total = 8.86 + 16.66
0 30
3
Cantidad total = 25.322 cm de insulina suministrados durante los primeros 30 días.
0 30
Como hay gran cantidad de combinaciones con las que se podría obtener el mismo
resultado, se puede verificar que:
Cantidad total =
ab
b
a
f (t )dt Acuma desde a hasta b,
donde:
ƒ(t) es la función de la razón de cambio instantáneo.
Acum a representa el valor acumulado justamente hasta el instante t = a.
Se observa que, la integral de la razón de cambio instantáneo representa,
exclusivamente, un incremento, que en este problema es el aumento de insulina y no la
cantidad total de insulina suministrada. Matemáticamente puede representarse como:
b
a
f (t )dt
a b
donde:
ƒ(t) representa la función de la razón de cambio instantáneo.
representa el incremento obtenido desde el instante t = a hasta el instante t = b.
ab
110
EXPLICACIÓN INTEGRADORA
El total de insulina suministrada está representada por la suma de la razón de cambio
promedio.
I
RCP 0.10 0.26 0.42 0.55 0.66 .... 0.18 37.62 cm
3
160
Cuyo valor será muy aproximado al obtener por medio de la integral de la razón de
cambio instantánea:
b
a
f (t ) dt
60
0
0.2 t e 007t dt 37.634
Entonces hay una equivalencia aproximada entre la suma de la razón de cambio
promedio y la integral definida:
RCP
160
60
0
(funciónde la razó de cambo instantánea) dt
Para obtener la cantidad total de insulina en términos de una integral, será:
I
b
a
f (t ) dt Acuma desde a hasta b.
Donde Acuma representa el valor acumulado hasta el instante t = a.
111
3.3 ÁREA BAJO LA CURVA
Algunos desiertos del norte del país se caracterizan porque durante el día son
demasiado calientes y durante la noche muy fríos. Para mantener constante la
temperatura en su casa, los habitantes de esa región tienen instalado un sistema
automático de clima artificial, el cual suministra calor durante la noche y frío durante el
día; así, se equilibra la temperatura interior con la del exterior.
Supongamos que se elabora un registro de datos, se encuentra la razón de cambio
promedio de todos los pares y datos consecutivos, se grafica la razón de cambio
promedio y se obtiene una función que pase lo más cercanamente posible por todos los
puntos de la gráfica. Esta función se llama razón de cambio instantáneo.
La función ƒ(t) que describe la velocidad o razón del cambio instantáneo con que el
sistema de clima artificial suministra calor o frío es
ƒ(t) = 200 cos
t
12
50 cientos de BTU/h,
donde:
t está dada en horas para t [0,24]
está dado en radianes.
La unidad de medida es el BTU (British Thermal Unit: Unidad Térmica Británica).
Completa la siguiente tabla, sustituyendo cada valor de “t” en la función f(t) y evaluando
dicha función.
t
ƒ(t)
0
2
223.2
4
6.965
9
0
91.42
12
15
17.035
19
0
101.76
91.42
Recuerda que se están utilizando radianes y no grados; por lo tanto, debes usar
calculadora.
112
24
La gráfica de la función es:
Figura 11.
Los intervalos de t para los que el sistema de clima artificial calienta son:
0 t < 6.965 (muy temprano por la mañana)
17.035 < t ≤ 24 (después del atardecer).
El intervalo durante el cual el sistema de clima artificial enfría es
6.965 < t < 17.035.
Las regiones sombreadas en la figura 12 muestran el total de energía suministrada para
calentar.
Figura 12.
113
En la figura 13 se muestra la cantidad de energía que gasta el sistema para enfriar.
Figura 13.
La cantidad de energía que gasta el sistema de clima artificial se observa en la figura 14.
Figura 14.
Esto se debe a que el sistema de clima artificial consume energía eléctrica tanto para
calentar la habitación como para enfriarla.
114
Al calcular la energía que el sistema emplea para calentar se debe recordar que la
integral definida de la función de la razón de cambio instantáneo representa el área bajo
la curva comprendida en el intervalo definido por los límites de integración.
Definición
El área bajo la curva representa la energía total que consume el sistema de clima
artificial, ya sea para calentar o para enfriar. Esto último puedes verificarlo multiplicando
las unidades de la base (horas) por las unidades de altura (cientos de BTU/h).
ciento de BTU
hora
base x altura = horas x
Al simplificar las horas, queda:
base x altura = cientos de BTU, que son las unidades de energía.
De acuerdo con esto, debes evaluar la integral de la función de razón de cambio
instantáneo para obtener la energía que consume el sistema de clima artificial, ya sea
para calentar o enfriar.
Mas si se quiere obtener la energía que consume el sistema para calentar, debemos
observar las regiones que se encuentran por encima del eje X, a fin de determinar los
límites de integración y sumar las áreas de ambas regiones. Por lo tanto:
Energía para calentar =
6.965
0
t
200 cos 12 50 dt
6.965
t
12(200)
sen
50t
=
12
0
24
17 .035
t
200 cos 12 50 dt
24
t
12(200)
sen
50t
12
17 .035
12(200)
(6.965)
(0 )
=
sen
506.965 0 + ...
sen
12
12
12(200)
(24)
(17.035)
=
sen
5024 17.035
sen
12
12
= [763.94(0.968 0) + 348.25] + [763.94(0 + 0.968) + 50(6.965)]
= 2 175.48 cientos de BTU para calentar.
115
El mismo razonamiento se aplica para calcular la energía que consume el sistema para
enfriar, es decir, con base en la región que se encuentra por debajo del eje X se
determinan los límites de integración y posteriormente se resuelve la integral.
Energía para enfriar =
t
200 cos 12 50 dt
17.035
6.965
t
12(200)
=
sen
50t
12
=
17.035
6.965
12(200)
(17.035)
(6.965
sen
5017.035 6.965
sen
12
12
= 763.94 (0.968 – 0.968) + 50(10.07)
= 763.94 (1.936) + 503.5
= 1478.98 + 503.5
= 975.48 cientos de BTU para enfriar.
El signo negativo indica que la región se encuentra por debajo del eje X, mientras que un
signo positivo señalaría que se ubica por encima del eje X.
El cálculo de la energía que gasta el sistema de clima artificial se determina mediante la
suma de ambos valores, sin considerar su signo, puesto que el sistema gasta energía
para calentar y enfriar. Así:
Energía total gastada = 1 087.74 + 975.48 + 1 087.74
= 3 150.96 cientos de BTU.
De lo anterior se concluye que el sistema de clima artificial en ciertas ocasiones calienta
y en otras enfría la casa, pero
¿Cuál es el efecto neto del sistema de clima artificial al cabo de las 24 horas?
¿Calienta más de lo que enfría la casa?
Hay dos formas para encontrar el resultado:
116
Una de ellas es obteniendo la integral de 0 a 24.
Efecto neto =
24
0
t
200 cos 12 50 dt
24
t
12(200)
sen
50t
=
12
0
=
12(200)
(24)
(0 )
sen 12 sen 12 50(24 0)
= 1200 cientos de BTU.
Como el signo es positivo, el efecto neto del sistema es que calentó la casa en vez de
enfriarla.
La otra manera es sumando las integrales correspondientes a las regiones sombreadas.
Efecto neto = A1 – A2 + A3 =
6.695
0
f (t )dt
17 .035
6.965
f (t )dt
24
17 .035
f (t )dt
= 1087.74 – 975.48 + 1087.74
= 1200 cientos de BTU,
que es el mismo valor calculado por medio de la integral de 0 a 24
Dado que la integral definida representa el área bajo la curva, o bien, el efecto total de
una función la razón de cambio instantáneo y, como las unidades de esa área se
obtienen al multiplicar las unidades del eje horizontal por las del eje vertical, lo mismo
que cuando se multiplica la base por la altura, su cálculo ofrece muchas combinaciones
y, por consiguiente, de aplicaciones en diferentes ramas del conocimiento.
117
ACTIVIDAD DE REGULACIÓN
Resolver el siguiente problema.
En una isla del Pacífico Sur, la temperatura varía regularmente de acuerdo con la
dT
1
2 t
ecuación
sen
60 sen 2 t , donde T es la temperatura en °F y t el
dt
3
365
dT
tiempo en días. Buscar la ecuación de la temperatura real (sugerencia: integrar
).
dt
EXPLICACIÓN INTEGRADORA
La función que describe la velocidad o razón de cambio instantánea con el que un
sistema de clima artificial suministra calor o frío, es:
f (t ) 200 cos
t
12
50
Por lo tanto, para calcular el efecto neto de consumo de energía tanto para enfriar como
para calentar el ambiente, es:
t
200 cos 12 50 dt
24
0
Dicha integral definida, representa a la vez el área bajo la curva de la función f(t).
118
3.4 ÁREA ENTRE CURVAS: UTILIDADES
Para calcular las utilidades o ganancias de una empresa se deben considerar dos
factores fundamentales: los ingresos y los costos. Los ingresos representan el dinero
total que entra en la empresa, mientras que los costos representan el total de dinero que
sale de la misma. De modo que, si por un lado entra dinero y por otro sale, la diferencia
de lo que entra menos lo que sale son las utilidades. Así.
U = I C,
Donde:
U : utilidades
I : ingresos
C : costos
Supongamos que una empresa decide patrocinar durante un año a popular cantante.
Durante los primeros meses los ingresos aumentaban y los costos disminuían con el
transcurso del tiempo. Al término del séptimo mes la situación se revirtió: los ingresos
disminuían y los costos aumentaban considerablemente. Los empresarios decidieron
realizar un estudio económico a fin de pronosticar el momento más propicio para
cancelar los contratos y dar por terminado el negocio.
El estudio económico consistió en el registro de datos, primero de ingresos y después de
costos, se determinó la razón de cambio promedio de todos los pares de datos
consecutivos y se obtuvo la gráfica de los valores calculados. Posteriormente se obtuvo
la función que más se aproximaba a la gráfica realizada (razón de cambio instantáneo).
Con lo anterior se determinó que la tasa de ingresos mensuales que percibía la empresa
estaba representada por la función.
I(t) =
1
(t 6) 2 5 cientos de millones de dólares/mes,
6
mientras que la tasa de costos mensuales estaba representada por la función
C(t) =
2
1
(t 5 ) 0.5 cientos de millones de dólares/mes
4
Ahora veamos las diferentes situaciones que se le presentaron a la empresa durante el
estudio.
119
Una de ellas es el cálculo de los ingresos durante los primeros cuatro meses de
patrocinio. Como la función I(t) representa una razón de cambio instantáneo, si
aplicamos la fórmula del problema anterior.
b
a
f (t )dt
a b
obtendremos el incremento de los ingresos desde el instante t = 0 hasta el instante t = 4,
así:
4
0
f (t )dt
04
Como se trata de un incremento, , a partir de t = 0, entonces se está obteniendo la
0 4
cantidad total del ingreso; antes de t = 0 no había nada más; por consiguiente, los
ingresos totales, I, cuando el tiempo está definido en el intervalo 0 ≤ t ≤ 4 se calculan
mediante la integral.
I =
0 4
1
( t 6 ) 2 5 ;
0 6
4
o sea,
4
1
(t 6) 3 5t ,
I =
0 4
6
(
3
)
0
que es
I =
0 4
1
( 4 6) 3 (0 6) 3 5( 4 0) ,
18
o también
I =
0 4
1
( 8 216) 20 .
18
Por lo tanto,
I = 8.444 cientos de millones de dólares (CMD)
0 4
120
Los costos totales durante los primeros cuatro meses de patrocinio se obtienen del
mismo modo, es decir, también se calcula una integral. Así:
C =
0 4
4
0
1
2
4 (t 5) 0.5 dt ,
o sea,
4
1
C =
( t 5) 3 0.5t ,
0 4
4(3)
0
que es
C =
1
( 4 5) 3 (0 5) 3 0.5( 4 0) ,
12
C =
1
( 1 125) 2 .
12
0 4
o también
0 4
Por lo tanto,
C = 12.333 (CMD).
0 4
Para calcular las utilidades de la empresa en ese mismo período se debe recordar que:
U = I – C,
Donde:
U : utilidades
I : ingresos
C : costos
Entonces las utilidades serán:
U I C ,
04
o sea,
o bien,
04
04
U 8.444 12.333 ,
04
U 3.888 CMD
04
121
Como las utilidades calculadas son negativas, en los primeros cuatro meses se
registraron solamente pérdidas.
Veamos otro procedimiento
Si primero se restan las funciones I(t) y C(t) y después se integra la diferencia obtenida,
la integral sería:
U
04
4
0
(I C )dt
o sea,
U
04
4
'0
1
1
2
2
(t 6) 5 (t 5) 0.5 dt ;
4
6
así
U 3.888 CMD,
04
que representa el mismo valor calculado. Este procedimiento consiste en obtener el área
entre dos funciones de t, f y g. Primero se calcula el área bajo la función f (figura 15).
Figura 15.
Después se calcula el área bajo la función g (figura 16).
122
Figura 16.
Se restan ambas áreas (figura 17).
Figura 17.
123
Así, si se aplica el cálculo para encontrar dichas áreas se obtienen las siguientes
expresiones:
b
Área bajo la función f =
f dt
Área bajo la función g
Área entre ƒ y g =
a
b
a
g dt
b
b
a
a
f dt
g dt .
La última expresión también se puede escribir como:
Área entre ƒ y g =
b
a
(f g ) dt
Al graficar las funciones C(t) e I(t) sobre el mismo plano cartesiano se obtiene la figura
18. El valor de las abscisas, o de los puntos de intersección 2.15 y 8.649 se encontró
mediante calculadora. Puedes aproximarte a los mismos valores por medio del método
gráfico para resolver sistemas de ecuaciones simultáneas.
Figura 18
Únicamente hemos calculado las áreas bajo la curva C(t) e I(t) de 0 a 4 meses, y la
diferencia I(t) – C(t), en el mismo periodo.
124
Otra forma para calcular las utilidades de 0 a 4 meses es calculando las utilidades,
U = I – C, de 0 a 2.15 meses (figura 18) y las utilidades para 2.15 a 4 meses. Observa
que cuando t = 2.15, se tiene el instante en el cual las dos curvas se intersectan,
entonces:
U
0 2.15
I C
0 2.15
0 2.15
Al aplicar la forma simplificada, puesto que son los mismos límites de integración, se
obtiene:
U
0 2.15
2.15
0
1
1
2
2
(t 6) 5 (t 5) 0.5 dt ,
4
6
o bien,
U 1.92 9.56 ,
0 2.15
o también
U 7.64 CMD.
0 2.15
La figura 19 ilustra este cálculo. La región sombreada representa más costos que
ingresos, 7.64 CMD, siendo ésta el significado del signo negativo.
Figura 19
125
Para el siguiente periodo.
U
2.15 4
I C ,
2.15 4
2.15 4
resulta que:
U
2.15 4
1
1
(t 6) 2 5 (t 5) 2 0.5 dt ,
2.15
4
6
4
o bien,
U 6.52 2.77 ,
2.15 4
o también
U 3.75 CMD.
2.15 4
La figura 20 representa este cálculo.
Figura 20
La región sombreada representa más ingresos que costos, 3.75 CMD.
126
Para calcular las utilidades de 0 a 4 meses se deben sumar las dos utilidades calculadas
anteriormente, es decir,
U U U
0 4
0 2.15
2.15 4
,
o sea,
U 7.64 3.75 ,
04
o bien,
U 3.89 CMD.
04
Llenar por medio de la forma simplificada los espacios en blanco de la siguiente tabla.
t(meses)
U(CMD)
1
2
4*
5
6
7
8
9
Recuerda que la forma para hallar el área entre dos curvas es: A
En nuestro problema sería U
a b
10
12
b
a
(f g ) dt .
b
a
(I C ) dt .
Al utilizar a = 0 y b = t meses, deberás obtener una tabla como la siguiente.
t(meses)
1
U(CMD) 5.64
(*) Valor ya calculado
2
4*
3.89*
5
0.14
6
127
7
8.36
8
9
11.25
10
12
9
De acuerdo con la tabla anterior, para que la empresa comenzara a obtener ganancias,
debieron transcurrir cinco meses, puesto que hasta ese momento los ingresos
superaban los costos totales, de ahí que el signo de las utilidades totales sea positivo: +
0.14 CMD.
Asimismo se puede apreciar en la tabla que debieron transcurrir nueve meses para que
la empresa obtuviera el mayor beneficio. Ni antes ni después. Para los empresarios esto
significaba estimar un comportamiento futuro, es decir, pronosticar la situación
económica de su empresa a corto plazo.
Realizar este análisis es fundamental para la toma de decisiones, sobre todo por el
apoyo que brinda el manejo de las computadoras, pues así no se corren riesgos
innecesarios y puede aumentarse la productividad tanto en los negocios como en otras
esferas del saber.
128
EXPLICACIÓN INTEGRADORA
Otro de los problemas en donde se muestran las aplicaciones del Cálculo es en las
utilidades de una empresa.
Utilidades = Ingresos – Costos
Función que representa la tasa
de ingresos mensuales
1
I(t) = (t 6) 2 0.5
6
Función que representa la tasa
de costos mensuales
1
C(t) = (t 5) 2 0.5
4
La cantidad total de ingresos en los
primeros 4 meses se obtiene de evaluar
4
1
I = (t 6) 2 0.5 dt 8.444 (CMD)
0 6
La cantidad total de los costos en los
mismos 4 meses resulta de evaluar
4
C = 1 (t 5) 2 0.5 dt 12.333 (CMD)
0 4
U=I–C
U = 8.444 – 12.333
U = -3.888 CMD
En los primeros 4 meses se
registraron solamente pérdidas
129
Otro procedimiento para llegar a los mismos resultados es al resolver la integral:
U
4
0
(I C ) dt 3.888 (CMD ) , cuya interpretación gráfica representa el área entre
las funciones I(t) y C(t) para el intervalo de 4 meses.
U = AT = –7.64 + 3.75 = –3.89 (CMD)
130
3.5 CÁLCULO E INTERPRETACIÓN
INTEGRACIÓN
DE
LA
CONSTANTE
DE
Existen bacterias patógenas (causan enfermedades) y bacterias inofensivas que tienen
importante función en diversos procesos industriales, sin olvidar aquéllas que destacan
por su importancia en el equilibrio del mundo viviente y por su aplicación en la medicina.
Al registrar cada hora el número aproximado de bacterias que contiene cierto cultivo y,
posteriormente calcular la razón de cambio promedio para pares de datos consecutivos,
con el fin de graficar los valores encontrados y obtener la función que más se aproxime a
la curva trazada, la función que resulta es:
f (t ) 1000 e 2t ,
Donde:
t: medida en horas
ƒ(t): número de bacterias/horas.
Como ƒ(t) representa la función de la razón de cambio instantáneo, al calcular su integral
definida se obtiene el incremento de la población en el periodo definido por los límites de
la integración; pero si en lugar de evaluar la integral definida de la función de la razón de
cambio instantáneo se calcula una integral indefinida, se obtiene una función que
representa el valor de la variable en cualquier instante, t.
2t
Con base en la función de la razón de cambio instantáneo ƒ(t) = 1000 e bacterias/horas
llenar los espacios en blanco de la siguiente tabla:
t (horas)
f(t)
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
bacterias
horas
1000.0
1491.8
2225.5
3320.1
4953.0
7389.1
131
La gráfica para todos los puntos de la tabla tiene la siguiente forma:
Figura 21
Ahora determinaremos la integral indefinida de la función de la razón de cambio
instantáneo para obtener la función de la población, P(t), que nos proporcionará la
cantidad de bacterias en el tiempo, t.
Se tiene que:
P (t ) f (t )dt,
entonces,
2t
P (t ) 1000 e dt;
Como 1000 es un valor constante se puede colocar fuera de la integral, en
consecuencia:
P(t ) 1000 e
2t
dt .
Al completar la integral queda:
P (t )
1000 2t
e (2) dt,
2
132
y al evaluar dicha integral se obtiene:
P(t ) 500 e 2t C ,
Donde:
P(t) representa la función de la población (cantidad de bacterias).
C es la constante de integración, cuyo valor depende de las condiciones específicas del
problema.
Establezcamos las condiciones del problema a partir de la función de la población:
P(t ) 500 e 2t C ,
Si se considera que la constante de integración vale cero, entonces,
P(t ) 500 e 2t .
ACTIVIDAD DE REGULACIÓN
Para la función P(t ) 500 e 2t , llenar los espacios en blanco de la siguiente tabla:
t (horas)
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
P(t) (bacterias)
610.7
911.1
1359.1
2027.6
3024.8
133
La gráfica de estos puntos es la siguiente:
Figura 22
Si se considera que la constante de integración toma otros valores además de cero,
entonces:
Figura 23.
134
La función P(t ) 500 e 2t C representa una familia de curvas porque la constante de
integración puede tomar distintos valores; sin embargo, solamente una de estas curvas
es la que caracteriza a nuestra población de bacterias porque es la única que
corresponde a las condiciones del problema, que pueden determinarse de la siguiente
manera: se observa una muestra de cultivo a través del microscopio y se estima la
cantidad de bacterias, a la vez que se determina el instante en que se hizo la
observación: Supongamos que en el instante t = 0.6 (horas) se observó la muestra a
través del microscopio y se estimó una población de 6660 bacterias. Cuando el instante
de observación corresponde a cero horas, se dice que la cantidad de bacterias en ese
instante es la condición inicial del experimento.
Busquemos las coordenadas (0.6, 6660) en alguna gráfica de la familia de curvas.
Figura 24
De acuerdo con la figura 24, la curva que satisface las condiciones del problema es la
que tiene por constante de integración C = 5000.
En conclusión:
El valor de la constante de integración, C, puede determinarse solamente si se
conoce el valor de la integral, P(t), para un determinado valor de la variable, t.
135
Para determinar analíticamente el valor de la constante de integración, C, se parte de la
función de la población:
P(t ) 500 e 2t C .
Se sustituye tanto el valor estimado de la población, P(t), como el instante, t, en que fue
obtenido.
Por lo tanto:
P(t ) 500 e 2t C ,
se convierte en
6660 500 e 2(0.6) C ,
igual que
6660 500(3.32) C ,
o bien
6660 1660 C ,
o también
6660 1660 C .
Al simplificar resulta:
C = 5000 bacterias.
ACTIVIDAD DE REGULACIÓN
Determinar el valor de la constante C (número de bacterias) para las coordenadas
(0.5,7000) correspondientes a la función P(t ) 500 e 2t C .
Nota. Recuerda que e = 2.7182
136
EXPLICACIÓN INTEGRADORA
f(t) = 1000 e
2t
función que representa el número e
incremento de bacterias que
contiene cierto cultivo
Si se calcula
La integral definida
de f(t)
La integral indefinida
de f(t)
f (t ) 1000 e 2t dt
Se obtiene el
incremento de la
población de
bacterias en el
período definido por
los límites
Se obtiene una
función que
representa la
cantidad de
bacterias en el
tiempo t.
2t
P(t) = 500 e + C
2t
La función P(t) = 500 e + C, representa una familia de curvas porque la constante de
integración puede tomar distintos valores. Si se establecen las condiciones del problema,
se puede determinar C.
137
RECAPITULACIÓN
Determinar una variable fenómeno
Registrar la variable a
Intervalos regulares de tiempo
Calcular la razón de cambio
promedio de todos los pares
de datos consecutivos
Graficar la razón de cambio promedio
Realizar un diagrama de barras
Obtener la función que más se
aproxime a la gráfica: función de la
razón de cambio instantáneo
Obtener el área bajo la curva,
(valor total de la variable)
Integrar la función para encontrar
el valor total de la variable (área
bajo la curva)
Por este camino es imposible obtener
pronósticos confiables
Por este camino se pueden obtener
pronósticos más confiables
138
ACTIVIDADES INTEGRALES
4
2
1. Con base en ƒ(t) = 0.0001 (t – 13) – 0.169 (t – 13) + 25.7
temperatura promedio, f (t ) , para los siguientes intervalos:
Intervalo (semanas)
026
2652
013
ºC, encontrar la
1326
ƒ(t) (ºC)
3
2. A partir de ƒ(t) = 0.2e0.07t cm /día calcular la cantidad de insulina suministrada al
paciente.
3
Intervalo cm de
(días)
insulina
010
1020
2030
3040
4050
5060
139
AUTOEVALUACIÓN
A continuación se presenta la solución de las actividades integrales, compara tus
respuestas y si tuviste alguna duda regresa al capítulo o bien consulta a tu asesor de
contenido.
1.
Intervalo (semanas)
ƒ(t) (ºC)
026 2652 013 1326
16.75 28.95 16.75 16.75
2.
3
Intervalo cm de
(días)
insulina
6.3594
010
1020 10.3005
8.662
2030
6.0627
3040
3.8852
4050
2.3637
5060
37.6335
140
RECAPITULACIÓN GENERAL
INTEGRACIÓN Y APLICACIONES
INTEGRAL INDEFINIDA
TÉCNICAS DE INTEGRACIÓN
APLICACIONES DEL CÁLCULO
INTEGRAL
ANTIDERIVADA O
FUNCIÓN PRIMITIVA
CAMBIO DE VARIABLE
VALOR PROMEDIO DE UNA
FUNCIÓN Y ÁREA BAJO LA
CURVA
CONCEPTO DE
INTEGRAL INDEFINIDA
DETERMINACIÓN DE
LA CONSTANTE
COMPARACIÓN ENTRE
INTEGRAL INDEFINIDA
Y DEFINIDA
ALGUNOS CASOS
BÁSICOS DE LA
INTEGRAL INDEFINIDA
INTEGRACIÓN POR PARTES
INTEGRACIÓN DE
FUNCIONES RACIONALES
POR FRACCIONES
PARCIALES:
INTEGRAL DE LA RAZÓN DE
CAMBIO INSTANTÁNEO
ÁREA BAJO LA CURVA
-DENOMINADOR FORMADO
POR UNA FUNCIÓN LINEAL
ÁREA ENTRE CURVAS:
UTILIDADES
-DENOMINADOR FORMADO
POR FACTORES LINEALES
(DE 1° GRADO) QUE NO SE
REPITEN
CÁLCULO E INTERPRETACIÓN
DE LA CONSTANTE DE
INTEGRACIÓN
- DENOMINADOR FORMADO
POR FACTORES DE 2°
GRADO QUE NO SE REPITEN
141
ACTIVIDADES DE CONSOLIDACIÓN
En este apartado podrás poner en práctica los conocimientos que has adquirido a lo
largo del contenido del fascículo.
Lee con atención lo que se te pide antes de resolver los siguientes ejercicios.
1. Responde el siguiente ejercicio.
Sea la función y = f(x) = x
3
a) Integra la función derivada.
b) Grafica el resultado del inciso anterior para cuando C =1, C = 0 y C = –2.
2. Coloca los números 1, 2 y 3 en los paréntesis según la técnica de integración
adecuada para resolver la integral respectiva.
x
a) (
)
b) (
)
x
c) (
)
d) (
)
5 2x 2
dx
1. Cambio de variable.
2. Integración por partes
sen 3x dx
( 4x 2 13x 9)
x 3 2x 2 3 x
(5x 2 3x 2)
x 3 x 2 2x
dx
3. Fracciones parciales
dx
142
3. Responde lo siguiente:
a) A partir de ƒ(t) = 200 cos
t
12
blanco de las siguientes tablas:
t
ƒ(t)
1
50 cientos de BTU/hora, llenar los espacios en
6
8
Intervalo *Energía
(meses
para
calentar
12 – 24
0 12
3 21
(*) Cientos de BTU.
11
13
18
* Energía
para
enfriar
23
*Efecto
neto
1
1
(t 6) 2 5 CMD/mes y de C(t ) (t 5)2 0.5 CMD/mes,
4
6
completar la siguiente tabla:
b) A partir de I(t) =
Intervalo *ingresos
(meses)
totales
I(t)
1–3
3–8
8 – 10
* En CMD.
*Costos
totales
C(t)
*Utilidades
totales
U(t)
2t
c) A partir de ƒ(t) = 1000 e bacterias/hora llenar la siguiente tabla:
Intervalo
(horas)
3–6
4–6
5–6
Verificar que
6
3
Aumento de la
población
(bacterias)
f (t )dt P(3)
6
4
Población total
(bacterias)
f (t )dt P( 4)
6
5
f (t )dt P(5) .
Calcular la constante de integración si se observó a través del microscopio una
población de 200000 bacterias al cabo de: 1 hora, 2 horas y 3 horas (tres
condiciones específicas).
143
AUTOEVALUACIÓN
En este apartado podrás comparar tus resultados con los que te presentamos a
continuación, asimismo podrás identificar los aciertos y errores obtenidos en las
actividades de consolidación.
1. a) Familia de curvas polinomiales de grado 3.
b) La integración es el proceso inverso de la derivación, ya que esto se observa
gráficamente; además, se puede tener un número infinito de antiderivadas.
2. a) (1)
b) (2)
c) (3)
d) (3)
3.
a)
t
ƒ(t)
1
243.2
6
50
8
11
13
50 143.2 143.2
Intervalo *Energía * Energía
(meses
para
para
calentar
enfriar
12 – 24 1087.94 487.94
1087.94 487.94
0 12
795.5
3 21
975.89
(*) Cientos de BTU.
144
18
50
*Efecto
neto
600.00
600.00
180.38
23
243.2
b)
c)
Intervalo *ingresos
(meses)
totales
I(t)
1–3
4.5
3–8
23.06
8 – 10
6.89
* En CMD.
Intervalo
(horas)
3–6
4–6
5–6
*Costos
totales
C(t)
5.6
5.42
9.16
Aumento de la
población
(bacterias)
81175679
79886918
70364155
*Utilidades
totales
U(t)
1.1
17.64
2.28
Población total
(bacterias)
81450000
81450000
81450000
1 (horas)
1
2
C (bacterias)
196305 172701
C = constante de integración
145
3
1714
ACTIVIDADES DE GENERALIZACIÓN
Para complementar lo aprendido en este fascículo te recomendamos visitar el Museo
“Universum” de Ciudad Universitaria, donde encontrarás aplicaciones y conceptos del
Cálculo Diferencial e Integral.
Haz una lista de las integrales indefinidas con base en diferentes libros de Cálculo.
Pon a germinar unas cuantas semillas de frijol. Para tal efecto introduce algodón en un
frasco de vidrio de boca ancha y coloca, separadas por el algodón, las semillas de frijol;
posteriormente vacía un poco de agua en el interior del frasco. A los pocos días de
iniciado el experimento observa el crecimiento de una de las semillas anotando su altura
día con día en una tabla:
día
altura (cm)
1
2
3
4
5
6
7
...
Calcula la razón de cambio promedio de todos los pares de datos consecutivos y grafica
los valores de la razón de cambio promedio en una hoja de papel milimétrico para
obtener una gráfica como la siguiente:
Figura 25
146
La función que representa esta gráfica anterior es función de la razón de cambio
instantáneo, y el área bajo la curva representa la altura total de la planta hasta el día en
que se efectúo el último registro. Para calcular el área bajo la curva puedes utilizar el
método de barras.
Sobre la gráfica anterior dibuja, de izquierda a derecha, barras del mismo ancho cuya
altura sea el valor de función en los puntos medios de los intervalos.
Figura 26
Para mejorar la precisión del cálculo del área, puedes aumentar el número de barras
disminuyendo el ancho de las mismas.
Figura 27
147
El área bajo la curva se obtiene al sumar el área de todos los rectángulos, obtén esta
suma y verifica que el resultado es la altura de tu planta.
Para obtener el efecto total de una función que representa un fenómeno dinámico
(integral definida o el área bajo la curva) que se encuentre representando gráficamente
como el experimento anterior, puedes aplicar el procedimiento (exclusivo para calcular
integrales definidas) que se basa en el siguiente razonamiento: El área bajo la curva es
proporcional al peso del papel limitado por la misma curva, el eje horizontal y los límites
de integración. Entonces, si pesamos el papel bajo la curva, tendremos un indicativo del
área buscada. Para obtener el valor numérico del área, es necesario tener una medida
que sea considerada como unidad, (un pequeño rectángulo) y posteriormente se divide
el peso bajo la curva entre el peso del rectángulo y se multiplica el resultado por el valor
que represente dicho rectángulo, es decir, por su área.
Procedimiento
1. Sobre papel milimétrico grafica la función. No olvides indicar los límites de integración.
Figura 28
2. Delimita el área sombreada y pésala.
Peso del ejemplo: 7.2 g.
Figura 29
148
3. Recorta un pequeño rectángulo de dimensiones conocidas.
Figura 30
En este caso, el área del rectángulo (base x altura) es A = (6 $/h) (2h), o sea, A = $12.
No olvides multiplicar las unidades de los ejes coordenados
4. Pesa al pequeño rectángulo. Para este ejemplo es de 1.8 g.
Figura 31
5. Ahora divide el peso bajo la curva entre el peso del rectángulo. En nuestro caso sería:
7.2g
4.
1.8g
149
6. Multiplica el resultado por el área del rectángulo.
4($12) = $48.
No olvides las unidades ($).
El resultado representa la integral definida de la función dada.
Para mejorar la precisión de tus cálculos utiliza una balanza analítica del laboratorio de
física, recorta y pesa papel aluminio en lugar de papel milimétrico, el cual solamente
servirá como plantilla después de dibujar sobre él la gráfica.
Prueba con funciones sencillas.
6
a)
2
b)
4
c)
( x 1) dx .
6
( x 2 1) dx .
6
3
( x 2) dx .
150
BIBLIOGRAFÍA CONSULTADA
BAUM, Alan M. et. al.: Cálculo Aplicado. Limusa, México, 1992.
BOSCH, Guerra. et. al.: Cálculo Diferencial e Integral. Publicaciones Cultural, México,
1987.
DEL GRANDE, D.: Introducción al Cálculo Elemental. Harla, México, 1976.
FLORES, M. y Luque A.: Cálculo Diferencial. Fascículo I. Colegio de Bachilleres, México,
1994.
FRANK, A.: Cálculo Diferencial e Integral. (Serie Schaum). McGraw-Hill, México, 1994.
GOLDSTEIN, Larry J. et. al.: Cálculo
Hispanoamericana, México, 1990.
y
sus
Aplicaciones.
Prentice-Hall
GRANVILLE, W. A..: Cálculo Diferencial e Integral. Limusa, México, 1993.
JONSON, R. E. et. al.: Cálculo con Geometría Analítica. CECSA, México, 1987.
KLEPPNER, D. R.: Curso rápido de Cálculo Diferencial e Integral. Limusa, México, 1975.
LEITHOLD, L.: El Cálculo con Geometría Analítica. Harla, México, 1982.
LUQUE A. y Flores M.: Cálculo Diferencial. Fascículo III. Colegio de Bachilleres, México,
1994.
151
METT, C. L. et al.: Cálculo con Aplicaciones. Limusa, México, 1991.
PHILLIPS, H. B.: Elementos de Cálculo Infinitesimal. UTHEA, México, 1960.
PURCELL, E. J.: Cálculo Diferencia Integral. Prentice Hall, México, 1989.
SWOKOWSKI, E. W.: Introducción al Cálculo con Geometría Analítica. Grupo Editorial
Iberoamericana, México, 1979.
ZILL, Dennis G. Cálculo con Geometría Analítica. Grupo Editorial Iberoamérica, México,
1987.
152
DIRECTORIO
Dr. Roberto Castañón Romo
Director General
Mtro. Luis Miguel Samperio Sánchez
Secretario Académico
Lic. Filiberto Aguayo Chuc
Coordinador Sectorial Norte
Lic. Rafael Torres Jiménez
Coordinador Sectorial Centro
Biol. Elideé Echeverría Valencia
Coordinadora Sectorial Sur
Dr. Héctor Robledo Galván
Coordinador de Administración Escolar
y del Sistema Abierto
Lic.José Noel Pablo Tenorio
Director de Asuntos Jurídicos
Mtro. Jorge González Isassi
Director de Servicios Académicos
C.P. Juan Antonio Rosas Mejía
Director de Programación
Lic. Miguel Ángel Báez López
Director de Planeación Académica
M.A. Roberto Paz Neri
Director Administrativo
Lic. Manuel Tello Acosta
Director de Recursos Financieros
Lic. Pablo Salcedo Castro
Unidad de Producción Editorial