ZVVRZ = + ( ) 1 wR C Av ww RRCC wR C wR C
Anuncio

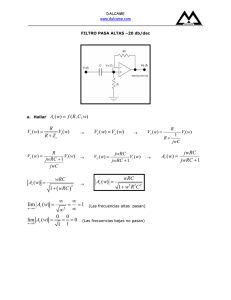
DALCAME www.dalcame.com __________________________________________________________________________ FILTRO PASABANDA: BANDA ANCHA a. Hallar Av ( w) = f ( R, C , w) Z c1 Vx = Vi R1 + Z c1 Vy = R2 Vx R2 + Z c 2 → → 1 jwC Vx = V 1 i R1 + jwC Vo = R2 R2 + 1 jwC2 Vx → Vx = 1 Vi (1) jwR1C1 + 1 → Vo = jwR2C2 Vx (2) jwR2C2 + 1 Reemplazo 1 en 2 Vo = ⎤ jwR2C2 ⎡ 1 V i⎥ ⎢ jwR2C2 + 1 ⎣ jwR1C1 + 1 ⎦ Vo = → jwR2C2 Vi ( jwR2C2 + 1)( jwR1C1 +1) Vo jwR2C2 = 2 Vi − w R1 R2C1C2 + jwR2C2 + jwR1C1 + 1 Av ( w) = wR2C2 (1 − w R R C C ) + ( wR C 2 2 1 b. Hallar wc y f c 2 1 2 2 2 + wR1C1 ) 2 DALCAME www.dalcame.com __________________________________________________________________________ 1 = 2 wR2C2 (1 − w R R C C ) + ( wR C 2 2 1 ⎛ ⎜ ⎝ 2 1 2 2 2 + wR1C1 ) (1 − w R R C C ) + ( wR C 2 2 1 2 1 2 2 (1 − w R R C C ) + ( wR C 2 2 1 2 1 2 2 2 + wR1C1 ) 2 2 2 ( ⎞ ⎟ = wR2C2 2 ⎠ ) 2 + wR1C1 ) = 2w2 R2 2C2 2 2 2 1 − 2 w 2 R1 R2C1C2 + w 4 R12 R2 2C12C2 2 + w 2 R2 2C2 2 + 2 w 2 R1 R2C1C2 + w 2 R12C12 = 2 w 2 R2 2 C2 2 1 + w4 R12 R2 2C12C2 2 − w2 R2 2C2 2 + w2 R12C12 = 0 Como: f H = 10 f L , entonces: fL = 1 2π R2C2 fH = 10 1 = 2π R2C2 2π R1C1 R2 C 2 = 10 R1C1 Lo reemplazo en la ecuación anterior: 1 + w 4 R12 C12 (10 R2 C2 ) 2 − w 2 (10 R1C1 ) 2 + w 2 R12C12 = 0 1 + 100 w4 R14C14 − 100 w2 R12C12 + w2 R12C12 = 0 100 w4 R14C14 − 99 w2 R12C12 + 1 = 0 w2 (100w2 R14C14 − 99 R12C12 ) + 1 = 0 w2 + 1 = 0 100w2 R14C14 − 99 R12C12 = 0 w = −1 99 R12C12 w = 100 R14C14 2 99 2π f H = 10 R1C1 w= → 99 fH = 20π R1C1 0.1583 RC fL = 1 1 10 fL = 0.01583 R1C1 c. Hallar 99 100 R12C12 → Av ( f ) =f ( f , f c ) → → w= 99 10 R1C1 fH = 0.1583 R1C1 → DALCAME www.dalcame.com __________________________________________________________________________ ⎛ 0.1583 ⎞ ⎛ 0.01583 ⎞ 0.05 fr = ⎜ ⎟⎜ ⎟= R C R C ⎝ 1 1 ⎠ ⎝ 1 1 ⎠ R1C1 Av ( w) = R1C1 == → 0.05 fr ⎛ 0.05 ⎞ 10w ⎜ ⎟ ⎝ fr ⎠ 2 2 2 ⎛ ⎞ ⎛ ⎛ 0.05 ⎞ ⎞ 2 ⎛ 0.05 ⎞ ⎜1 − 10 w ⎜ ⎟ ⎟⎟ + ⎜11w ⎜ ⎟⎟ ⎜ f ⎝ r ⎠ ⎠ ⎝ ⎝ fr ⎠ ⎠ ⎝ Av (w) = d. Dibujar ⎛ f ⎞ 3.1415 ⎜ ⎟ ⎝ fr ⎠ 2 2 2 ⎛ ⎛ f ⎞ ⎞ ⎛ ⎛ f ⎞⎞ ⎜1 − 0.986 ⎜ ⎟ ⎟ + ⎜ 3.4557 ⎜ ⎟ ⎟ ⎜ ⎝ f r ⎠ ⎠⎟ ⎝ ⎝ fr ⎠ ⎠ ⎝ Av ( f ) Vs f Av (w) = ⎛ f ⎞ 3.1415 ⎜ ⎟ ⎝ fr ⎠ 2 ⎛ ⎛ f ⎞ ⎞ ⎛ ⎛ f ⎞⎞ ⎜1 − 0.986 ⎜ ⎟ ⎟ + ⎜ 3.4557 ⎜ ⎟ ⎟ ⎜ ⎝ f r ⎠ ⎠⎟ ⎝ ⎝ fr ⎠ ⎠ ⎝ 2 2 f Av ( f ) Av ( f ) db 0 0.1fc 0.5fc 0.8 fc fc 2 fc 4 fc 6 fc 8 fc 10 fc 0 0.3 0.8 0.9 0.9 0.8 0.6 0.5 0.4 0.3 0 -10 -2 -1 -1 -2 -4 -7 -9 -10 ⎛V ⎞ Av = 20 log ⎜ 0 ⎟ ⎝ Vi ⎠