Superficies

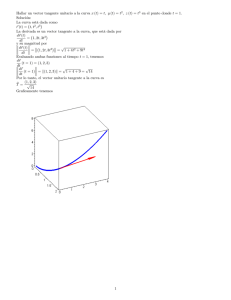
Superficies
Superficies
Superficies
Superficies
DEF. Una superficie, S, es un subconjunto de R3 imagen de
una aplicación:
~x : U ⊂ R2 → S ∈ R3
(u, v) 7→ ~x (u, v) = (x(u, v), y(u, v), z(u, v ))
~x se llama parametrización o carta.
Se dice que una superficie S es continuamente
diferenciable si x, y, z ∈ C 1 (U).
Superficies
Condición de regularidad
∂~x
∂~x ~
Los puntos de S para los que se cumple que
×
6= 0
∂u ∂v
se llaman puntos regulares.
∂~x ∂~x
y
no se
Esta condición significa que los vectores
∂u ∂v
anulan en ese punto y tienen direcciones distintas
Llamaremos punto singular a aquel en el que
∂~x
∂~x
×
= ~0
∂u ∂v
Se dice que S es una superficie regular si todos sus
puntos son regulares
Superficies
Curvas paramétricas
Si tomamos u = u0 tenemos ~x (u0 , v) = α
~ (v).
Esta curva se denomina curva v-paramétrica.
Si tomamos v = v0 tenemos ~x (u, v0 ) = α
~ (u).
Esta curva se denomina curva u-paramétrica.
(u, v) se llaman coordenadas curvilíneas
Interpretación geométrica de la condición de regularidad
En cada punto regular la curva u-paramétrica y la curva
v-paramétrica no son tangentes (el ángulo entre ellas no es
cero).
Superficies
Casos particulares de superficies regulares
Si f : U ⊂ R2 →R es una función diferenciable,
entonces
el grafo de f = (u, v, f (u, v)) ∈ R3 , (u, v) ∈ U es una
superficie regular.
Si f : R3 → R es una función diferenciable y a ∈ f (U) es un
valor regular de f , entonces
n
o
f −1 (a) = (x, y, z) ∈ R3 /f (x, y, z) = a
es una superficie regular.
a es un valor regular de f : R3 → R si para todo
∂f
∂f
∂f
~p = f −1 (a),
(~p ),
(~p) y
(~p) no se anulan a la vez
∂x
∂y
∂z
Superficies
Cambio de parámetros
Sea S una superficie parametrizada por
~x : U ⊂ R2 → S
(u, v) 7→ ~x (u, v)
Si tenemos otra aplicación
~y : Ū ⊂ R2 → S
(ū, v̄ ) 7→ ~y (ū, v̄ )
decimos que se trata de un cambio admisible de parámetros
si
∂(u, v) ∂(ū, v̄ ) 6= 0
Superficies
Plano Tangente
Sea P = ~x (u0 , v0 ) un punto regular de la superficie S y
consideremos una curva α
~ (t) = ~x (u(t), v(t)) contenida en S
pasando por P = α
~ (t0 ).
El vector tangente a α
~ (t) viene dado por:
α
~ ′ (t) =
d ~x (u(t), v(t))
∂~x du ∂~x dv
=
+
= ~xu u ′ + ~xv v ′
dt
∂u dt
∂v dt
Todos los vectores tangentes a la superficie S en un punto
regular están contenidos en un plano con vectores directores
~xu y ~xv . Este plano se llama plano tangente a S en P.
Superficies
Ecuación del Plano Tangente. Vector Normal
Todos los vectores tangentes a la superficie S en un punto
regular están contenidos en un plano con vectores directores
~xu y ~xv . Este plano se llama plano tangente a S en P.
Ecuación: (x, y, z) = ~p + λ~xu + ν ~xv
El vector normal a S en ~p = ~x (u0 , v0 ) viene dado por
~ = ~xu (u0 , v0 ) × ~xv (u0 , v0 )
N
k~xu (u0 , v0 ) × ~xv (u0 , v0 )k
La ecuación del plano tangente también se puede obtener:
((x, y, z) − ~p) · (~xu × ~xv )(u0 , v0 ) = 0
Superficies
Primera Forma Fundamental
DEF. Se llama Primera Forma Fundamental de la superficie
regular S en P ∈ S a la forma cuadrática
IP : TP (S) → R
~ 7→ IP (w
~)=w
~ ·w
~ = kw
~ k2
w
~ =α
Si w
~ ′ (t) = u ′ (t)~xu + v ′ (t)~xv ,
~ ) = (u ′ )2 E + 2u ′ v ′ F + (v ′ )2 G
IP (w
siendo E = ~xu · ~xu , F = ~xu ·~xv y G= ~xv · ~xv los coeficientes de
E F
la 1a Forma Fundamental:
F G
Superficies
Aplicaciones de la 1a Forma Fundamental
Longitud de un arco de curva: α
~ (t) = ~x (u(t), v(t))
s(t) =
=
Z
t
t0
Z t
t0
′
k~
α (t)kdt =
q
Z tp
I(~
α′ (t))dt
t0
(u ′ )2 E + 2u ′ v ′ F + (v ′ )2 Gdt
Elemento de longitud de arco: ds2 = Edu 2 + 2Fdudv + Gdv 2
Superficies
Aplicaciones de la 1a Forma Fundamental (II)
Ángulo que forman 2 curvas sobre una superficie
El ángulo que forman α
~ y β~ al cortarse en el punto
P =α
~
~ (t0 ) = β(t1 ) es el ángulo que forman los vectores
tangentes:
α
~ ′ (t0 ) = du~xu + dv ~xv , β~ ′ (t1 ) = δu~xu + δv ~xv
cos θ =
=
α
~ ′ (t0 ) · β~ ′ (t1 )
k~
α′ (t0 )kkβ~ ′ (t1 )k
√
du 2 E
duδuE + (duδv + dvδu)F + dvδvG
√
+ 2dudvF + dv 2 G δu 2 E + 2δuδvF + δv 2 G
Superficies
Aplicaciones de la 1a Forma Fundamental (III)
Ángulo que forman 2 curvas sobre una superficie
Si α
~ y β~ son curvas u y v paramétricas (respectivamente),
entonces:
~ ′ = ~xv
α
~ ′ = ~xu , β
y por ello
cos θ =
~xu · ~xv
F
=√ √
k~xu kk~xv k
E G
Las curvas paramétricas son ortogonales si F = 0
Superficies
Aplicaciones de la 1a Forma Fundamental (IV)
Área de una región acotada en una superficie
Sea R una región acotada contenida en una superficie S
parametrizada por ~x : U ⊂ R2 → S tal que R = ~x (Q) con
Q ⊂ U.
El área de R viene dada por:
Z Z
Z Z p
Área(R) =
k~xu × ~xv kdudv =
EG − F 2 dudv
Q
Q
Superficies
Orientación
DEF. Una superficie orientada es una superficie de dos caras
en la que se ha fijado una de las caras como lado positivo y la
otra cara como lado negativo.
Para indicar la orientación de S asignaremos a cada punto un
vector normal unitario que apunte hacia el lado positivo.
Si S está parametrizada por ~x : U ⊂ R2 → S sabemos que en
cada punto podemos obtener:
~ = ~xu × ~xv
N
k~xu × ~xv k
No todas las superficies admiten un campo de vectores de este
tipo (no tienen dos caras)
Superficies
Orientación (II)
DEF. Sean ~x e ~y dos parametrizaciones de S. Se dice que
∂(u, v) >0
definen la misma orientación cuando ∂(ū, v̄ ) ∂(u, v) <0
definen orientaciones opuestas si ∂(ū, v̄ ) Superficies
2a Forma Fundamental. Curvatura normal (I)
Sea α
~ una c.p.d.r. contenida en S pasando por
P=α
~ (s0 ) = ~x (u0 , v0 ) ∈ S y su vector curvatura en ese punto:
˙
~k(s0 ) = ~t(s
n(s0 )
0 ) = k(s0 )~
Este vector lo podemos descomponer en 2:
~
el vector proyección de ~k (s0 ) en la dirección de N.
~ n = (k ~n · N)
~ N
~
Vector Curvatura Normal: K
Curvatura Normal de S en la dirección de α
~:
~ = k cos θ
Kn = k ~n · N
~ 0 , v0 )
siendo θ el ángulo que forman los vectores ~n(s0 ) y N(u
Kn es la longitud de la proyección del vector curvatura
~k = k ~n sobre la normal a S en ~p
El signo de Kn viene dado por la orientación de S.
un vector contenido en el plano tangente a S.
~ g = ~k − K
~n
Vector Curvatura Tangencial o Geodésica: K
Superficies
2a Forma Fundamental. Curvatura normal (II)
Para calcular Kn tenemos en cuenta lo siguiente:
~
~
~ · ~t˙ = 0 ⇒ N
~ · ~t˙ = − d N · ~t
~ · ~t = 0 ⇒ d N · ~t + N
N
ds
ds

~
~
~

dN
∂N

′ + ∂N v ′

=
u

 ds
∂u
∂v
Escribimos los vectores:
y

′ (t)
′ +~
′

~
α
~
u
x
v
x

u
v

=
 ~t =
k~
α′ (t)k
IP (~
α′ (t))
sustituimos:
−1 ~ ′ ~ ′ Kn =
Nu u + Nv v · ~xu u ′ + ~xv v ′
′
IP (~
α (t))
~ u · ~xu + u ′ v ′ (N
~ v · ~xu + N
~ u · ~xv ) + (v ′ )2 N
~ v · ~xv
(u ′ )2 N
= −
IP (~
α′ (t))
Superficies
2a Forma Fundamental. Curvatura normal (III)
Denotando por:
~ u · ~xu ,
e = −N
~ u · ~xv = −N
~ v · ~xu ,
f = −N
~ v · ~xv
g = −N
llegamos a:
Kn =
(u ′ )2 e + 2u ′ v ′ f + (v ′ )2 g
IP (~
α′ (t))
Ahora definimos:
DEF. La Segunda Forma Fundamental de la superficie
regular S en P ∈ S es la forma cuadrática
IIP : TP (S) → TP (S)
~ w
~ 7→ IIP (w
~ ) = −(d N)(
~)·w
~ = (u ′ )2 e + 2u ′ v ′ f + (v ′ )2 g
w
~ = ~xu u ′ + ~xv v ′
siendo w
Superficies
2a Forma Fundamental. Curvatura normal (IV)
Interpretación de la 2a Forma Fundamental
~ ~t (s0 )) · ~t(s0 ) = N(
~ ~t(s0 )) · k(s0 )~n(s0 ) = Kn
IIP (~t(s0 )) = −(d N)(
La 2a Forma Fundamental aplicada sobre un vector
~ ∈ TP (S) nos da la curvatura normal de una
unitario w
~ (en P)
c.p.d.r. que pasa por P con vector tangente ~t = w
~ ∈ TP (S),
Para un vector cualquiera w
Kn =
IIP
IP
Superficies
2a Forma Fundamental. Cálculo de coeficientes
Vamos a ver otra forma de calcular de calcular
~ u · ~xu ,
e = −N
~ =
Dado que N
~ u · ~xv = −N
~ v · ~xu ,
f = −N
~ v · ~xv
g = −N
~xu × ~xv
~ · ~xu = N
~ · ~xv = 0
, se cumple que N
k~xu × ~xv k
Derivamos esas igualdades respecto a u y a v:
~ u · ~xu + N
~ · ~xuu
N
~ v · ~xu + N
~ · ~xuv
N
~ · ~xvu
~ u · ~xv + N
N
~ v · ~xv + N
~ · ~xvv
N
~ · ~xuu
=0⇒e=N
=0
(1)
=0
(2)
~ · ~xvv
=0⇒g=N
~ u · ~xv = N
~ · ~xuv = −N
~ v · ~xu
De (1)-(2) se deduce que: −N
~ · ~xuv
y además que f = N
Superficies
Teorema de Meusnier
Todas las curvas contenidas en S que tienen en P ∈ S la
misma tangente, tienen en ese punto la misma curvatura
normal.
Esto nos permite hablar de curvatura normal a lo largo de una
dirección en P.
~ ∈ TP (S), se llama sección normal de S en P en
DEF. Dado w
~ a la intersección de S con el plano que
la dirección de w
~
~ y a N(P).
contiene a w
Para una sección normal: |Kn | = k
Superficies
Direcciones y Curvas asintóticas
DEF. Se llama dirección asintótica de S en P a una dirección
de TP (S) tal que la curvatura normal es 0.
Por tanto las direcciones asintóticas vienen dadas por:
(u ′ )2 e + 2u ′ v ′ f + (v ′ )2 g = 0
DEF.Una curva o línea asintótica es una curva regular tal que
en todo punto su vector tangente es una dirección asintótica.
Su ecuación diferencial es: edu 2 + 2fdudv + gdv 2 = 0
Superficies
Curvaturas principales
DEF. Se denominan curvaturas principales en P a los valores
máximo (Kn1 ) y mínimo (Kn2 ) de la curvatura normal.
Se pueden obtener resolviendo la ecuación
(EG − F 2 )Kn2 + (2Ff − Eg − Ge)Kn + eg − f 2 = 0
Las direcciones en las que la curvatura toma valores extremos
se llaman direcciones principales en P.
Para calcularlas se debe resolver:
(Ef − Fe)du 2 + (Eg − Ge)dudv + (Fg − Gf )dv 2 = 0
DEF. Si una curva α
~ contenida en S es tal que su vector
tangente en todos sus puntos es una dirección principal, se
dice que α
~ es una línea de curvatura de S.
Superficies
Curvatura total y media
DEF. Curvatura total: K = Kn1 Kn2 =
DEF. Curvatura media: H =
eg − f 2
EG − F 2
1
Eg + Ge − 2Ff
(Kn1 + Kn2 ) =
2
2(EG − F 2 )
DEF. Se dice que S es una superficie mínima si sus curvas
asintóticas son ortogonales o (equivalentemente) si H = 0.
Superficies
Clasificación de los puntos de una superficie
Elíptico: K > 0
Hiperbólico: K < 0
Parabólico: K = 0
Plano: K = 0
Umbílico: Kn es constante, por tanto Kn1 = Kn2
Teorema Si todos los puntos de una superficie S son puntos
umbílicos, entonces S está contenida en una esfera o en un
plano.