EJERCICIOS PARA ESTUDIANTES 2011

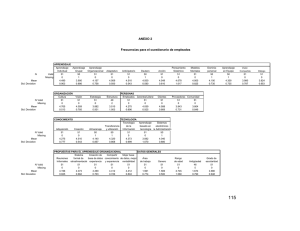
UNIVERSIDAD NACIONAL DEL ALTIPLANO
FACULTAD DE INGENIERÍA AGRÍCOLA
ESCUELA PROFESIONAL DE INGENIERÍA AGRÍCOLA
MÉTODOS ESTADÍSTICOS PARA LA
INVESTIGACIÓN
PROBLEMAS RESUELTOS
POR:
EDUARDO FLORES CONDORI
EDUARDO LUIS FLORES QUISPE
PUNO – PERÚ
2011
SUMATORIA
Al presentarse la suma de una secuencia numérica, en donde destaquemos cierta
secuencia u orden en los sumandos que se van a sumar, podemos esa suma
abreviarla bajo un signo, el que denominaremos sumatoria.
n
Tenemos por lo tanto que la sumatoria,
∑ak
k m
es una forma de expresar la
=
suma de los términos de una sucesión, términos que se obtienen dando a la
variable k valores enteros comprendidos entre dos límites escritos en la
parte superior del símbolo ∑ de sumatoria
Identificación,
Valor donde termina la sumatoria
n
Signo
sumatoria
∑x
i =1
Exprese las siguientes sumas mediante el símbolo
sumatoria.
a) S=12 + 22 + 32 + 42 + .... + n2
b) S= 1.2 + 2.3 + 3.4 + ..... + n(n+1)
c)
d)
d)
1 2
3
n
+ 2 + 3 + ... + n
2 2
2
2
1 2
3
n
S = + 2 + 3 + ... + n
2 2
2
2
3
2
4
S = 1 + 2 + 3 + .... + n +1 n
S=
Término a sumar
i
Valor por el cual comienza la suma
Ejemplos:
5
∑ xi
i =1
n
∑ xi
i =1
= x1 + x 2 + x3 + x 4 + x5
=x1 + x 2 + x3 + x 4 + ..... + x n
SUMATORIA-PROPIEDADES
1. La sumatoria de la suma de dos o más términos, es igual a la suma de las
sumatorias separadas de los términos.
n
n
n
i =1
i =1
i =1
∑ ( xi + y i ) = ∑ x i + ∑ y i
2. La sumatoria de la diferencia de dos o más términos es igual a la diferencia de las
sumatorias separadas de los términos.
n
n
n
i =1
i =1
i =1
∑ ( xi − y i ) = ∑ xi − ∑ y i
3. La sumatoria de una constante multiplicada por una variable es igual a la constante
multiplicada por la sumatoria de la variable.
n
n
i =1
i =1
∑ a.xi = a.∑ xi
4. La sumatoria de una constante es igual a la constante multiplicada por el número
que indique los límites de la sumatoria.
n
∑ a = n.a
x =1
En la práctica frecuentemente se comenten algunos errores, los cuales los
cuales mencionaremos para que no se incurra en ellos.
 n 
x
=
∑ x
∑
i =1
 i =1 
n
2
2
Es falso el tomar a
Otro error se comete es decir que
ya que son valores completamente diferentes
n
n
n
i =1
i =1
i =1
∑ xi yi = ∑ xi .∑ yi
ya que son términos diferentes.
EJERCICIOS.
1.—Escribe los términos de cada una de las siguientes sumatorias.
4
n
5
a )∑ ( X i + 2)
c )∑ U i (U i + 6 )
b )∑ f i X i2
i =1
i =1
d ) ∑ (YK2 − 4 )
N
i =1
4
e )∑ 4 X iYi
K =1
i =1
2.-- Dadas dos variables X e Y toman los valores X1= 2, X2= -5, X3= 4, X4= -8 y Y1= -3, Y2=-8,
Y3=10, Y4= 6. Calcula :
4
4
a )∑ X i
i =1

4
b)∑Y i
i =1
 
4

4
  i =1

i =1
n
4
h)∑ ( X i + Y i ) ( X i −Yi )
g)∑ X i .Y i 2
i =1
i =1
6
∑ X i = −4 y
Xi
∑
i
i =1
6
e)∑Y i 2
i =1
6
3.—Si
4
d)∑ X i2
i =1
f )  ∑ X i  .  ∑Yi 
 i =1
4
c)∑ X iYi
2
6
a )∑ (2X i + 3)
Halle:
6
b)∑ X i ( X i − 1)
i =1
= 10 ,
=1
c)∑ (X i − 5)2
i =1
i =1
4.—Dos variables U y V toman los valores U1= 3, U2= -2, U3= 5 y V1= -4, V2= -1, V3= 6,
respectivamente. Calcule:
3
3
b)∑ ( Ui +3 )(V i − 4 )
a )∑ U iV i
i =1
e )∑ U iV i 2
i =1
n
f)∑ (U i2 − 2V i 2 + 2)
i =1
4
∑Xi = 7
i =1
4
4
4
∑Yi = −3
2
2
i =1
3
5.—Dado
 3
 n 
c)∑V i
d)  ∑ U i   ∑V i 
i =1
 i =1   i =1 
n
U 
g)∑  i 
Vi 
i=1 
3
y
i =1
X iY i
∑
i
= 5 Halle:
=1
4
b)∑ ( X i − 3)( 2Y i + 1)
a )∑ (2 X i + 5Y i )
i =1
i =1
6.-- Desarrolle las siguientes sumatorias.
4
a )∑ xi =
i =1
3
5
b) ∑ f i .xi =
c )∑ x 2 =
i =1
x =1
3
d )∑ 3i =
i =1
3
e ) ∑ m( x − y ) =
m =1
f )∑ (x j + y j ) =
3
j
j =1
g )∑ f i ( xi − 20 ) = h)∑ (2 xi + 4 ) = i )∑ 5 x i = j )∑ (2 xi + y i − 6 z i ) = k )∑ (Ay j + j ) =
3
i =1
2
7
4
2
2
i =1
i =0
i =1
j =1
SUMATORIA----EJERCICIOS
Desarrolle las siguientes sumatorias
a) ∑ k
 12 
b) ∑  
K =1 k 
n) ∑ k (− 1)
i ) ∑ (k + 4 )(k − 1)
ñ) ∑ (20 − 2k )(− 1)
5
k =3
k =0
4
h) ∑ (k − 1)(k + 2 )
8
5
k −1
k
k =0
9
5
k
k =0
k = −1
4
c) ∑ (2k − 4 )
j ) ∑ (k + 3)(k − 4 )
o) ∑ (k + 3)(− 1)
d ) ∑ (2k + 1)
k ) ∑ (k 3 − k )
p ) ∑ (k + 5)
e) ∑ (5 − k )
l ) ∑ (k + 3k − 7 )
q )∑ (k + 1)
ll ) ∑ (3k 3 + 5k 2 + k − 3)
r ) ∑ (k 2 − 7 )
6
7
k =0
k = −3
k = −3
4
k
n
2
n +3
2
3k + 1
f )∑
2
k =0
6
k =4
k = −3
n −1
3k − 5k + 9
m) ∑
2k − 1
k = −2
g ) ∑ (k + 3)
k = −3
s ) ∑ (2k + 3)
2
3
2
3
k =1
k = −1
k =2
4
4
5
3
5
k = −2
k = −2
k =3
k
2
k = −2
Desarrolle las siguientes sumatorias
a ) ∑ (K + 1)
N
2
K =0
n
b) ∑ e − kx Senkx =
k =2
(−1) k −1 e kx
=
e) ∑
1+ k 4
k =0
n
m
i )∑ k k 4 + Sen
k =1
c) ∑ (2 − 3k ) =
5
k =0
f ) ∑ Lg (k + 1) =
kπ
=
2
2
2
k = −2
3
 kπ 
j ) ∑ Sen 2   =
k =0
 4 
2
d )∑ (2 + 3k )
k
(
− 1)
=
g )∑
k =1 k (k + 1)
n
n
k )∑ k 3 =
k =1
6
k −4
k =1
k
(
− 1) (k + 2 )
=
h) ∑
k
k =1 k (k + 1)2
n +1
(k + 3)(k + 4 )
l) ∑
1+ k 2
n
k = −2
1
=
k =3 (2k + 1)(2k − 1)
m
ll ) ∑
HOJA DE EJERCICIOS Nº 1
1. El valor de dos (2) variables X e Y, de una población es de 50 y 70 respectivamente.
i.
¿Cuál es la razón entre X e Y?
ii.
¿Cuál es la proporción de cada variable?
iii.
¿Cuál es el porcentaje de cada variable?
2. En una población de 240 datos y de dos variables X e Y el porcentaje de X [P(X) ] es de
35%.
i.
¿Cuál es valor de cada variable?
ii.
¿Cuál es la proporción de cada variable?
iii.
¿Cuál es la razón entre X e Y?
3. En una población de tres (3) variables X, Y y Z el valor de cada una de ellas es:
40 y 80 respectivamente.
i.
Halle la razón entre X e Y; entre Z y X y entre Y y Z.
ii.
Halle la proporción de cada variable.
iii.
Halle el porcentaje de cada variable.
60,
4. En una población de cinco (5) variables el valor de cada una de ellas es: X1 = 150; X2 =
200; X3 = 180; X4 = 160 y X5 = 300.
i.
Calcule la razón entre: X3 y X1; X4 y X2 y X5 y X1
ii.
Verificar que la suma de las proporciones es igual a uno (1)
iii.
Calcule el porcentaje de cada variable.
5. En una población de dos (2) variables X e Y la razón entre X e Y es de 5 a 3 y el total
de ellas es 240.
i.
Halle el valor de cada variable.
ii.
Calcule la proporción de cada variable.
iii.
Calcule el porcentaje de cada variable.
6. En una población de tres (3) variables X, Y y Z, la razón entre X y Z es de 5 a 9 y la
proporción de Y es 0,3, sí el total de la población es de 720.
i.
¿Cuál es el valor de cada variable?
ii.
Halle la razón entre X e Y, entre Z e Y.
iii.
¿Cuál es la proporción de cada variable?
iv.
¿Cuál es el porcentaje de cada variable?
7. Dada la siguiente tabla
i
1
2
3
4
5
6
7
8
Xi
3
5
7
8
0
9
1
4
Yi
5
7
2
9
3
0
6
3
8. Hallar el valor de las siguientes sumatorias:
8
∑( X
b)
4
∑( 3X
a)
i
∑ ( 2. X
e)
i
− Yi )
6
∑
f )
∑( X
j)
2 6
∑
i =3
( 2. X i + 4 )
 5

c ) X i .Yi 
 i =2

∑
∑X
i +1
− Yi −1 )
i
+1
7
∑( X
k)
i =4
i =2
9. Expresar en forma de sumatoria las siguientes expresiones:
∑( X
d)
i −1
− Yi+1 )2
2
i
− Yi 2 )
i =3
4
7
g)
7
2
i =2
7
i =2
∑
( X i2 + Y3 )2
i =2
+4)
 8

i ) ( X i + Yi 2 )
 i =2

− Yi )
i =1
i =1
6
i
∑X
h)
i =1
2
i
+3
a ) x1 + x2 + x3 + x3
b )x1 + x2 + x3 + x4 + x5
2
c )(cx3 + y0 ) + (cx4 + y0 ) + (cx5 + y0 )
X =
10. Sabiendo que:
2
n
i
Y=
y
n
∑Y
i
i =1
. Demostrar que:
n
n
n
∑( X
A)
i
− X ),( Yi − Y ) =
i =1
n
∑ X .Y −
i
2
i
i =1
 n 
 Yi 
n


= Yi −  i =1 
n
i =1
i =1
(
)
) =∑
− X =0
∑ (X
i
− X 0 ) − n. X − X 0 = 0
2
n
2
)
∑ (Y − Y )
n
i
F)
i =1
n−1

1  n 2 1 
=
Yi −
n − 1  i =1
n 

∑
∑

Yi 


2




i
i =1
n
∑
i
i =1
E)
i
 n

 Xi 


X i −  i =1 
n
∑ (X
D)
i =1
∑
i
−X
i =1
n
i
2
∑ (X
n
C)
n
∑ X .∑ Y
i =1
∑ (Y − Y ) ∑
n
B)
2
2
f )( x2 + x2 + x2 + x2 + x2 ) + 6
n
i =i
2
d )x2 + x3 + x4 + x5 + x6 + 5
e )(4 x3 + 7 ) + (4 x3 + 7 ) + (4 x3 + 7 ) + (4 x3 + 7 )
∑X
2
PROBLEMAS DE APLICACIÓN
(APLICACIONES: EXCEL SAS Y MINITAB)
1. Dada la serie histórica de descargas medias (m3/s) del rio Huancané, para el periodo 19592008. Calcule las frecuencias absolutas, relativa, acumulada, función de densidad y función
acumulada.
año
Q=m3/s
año
Q=m3/s
año
Q=m3/s
año
Q=m3/s
año
Q=m3/s
1959
1960
1961
1962
1963
1964
1965
1966
1967
25.00
20,00
13,00
26,00
29,00
22,00
29,00
20,00
19,00
1969
1970
1971
1972
1973
1974
1975
1976
1977
17,00
11,00
14,00
28,00
28,00
21,00
16,00
7,00
28,00
1979
1980
1981
1982
1983
1984
1985
1986
1987
24,00
21,00
18,00
20,00
19,00
17,00
21,00
17,00
21,00
1989
1990
1991
1992
1993
1994
1995
1996
1997
19,00
29,00
24,00
23,00
24,00
15,00
27,00
19,00
26,00
1999
2000
2001
2002
2003
2004
2005
2006
2007
23,00
10,00
14,00
23,00
21,00
27,00
27,00
28,00
26,00
9,00
1988
8,00
1998
23,00
2008
19,00
o
4
2
4
12
10
8
10
50
frec. Relat.
0.08
0.04
0.08
0.24
0.2
0.16
0.2
1
1968 26,00
1978
Solución problema 1
Número de intervalos de clase
m=
7
min =
7
max =
29
Ancho =
3
m
xi <=xi+1
1
7
10
2
10 13
3
13 16
4
16 20
5
20 23
6
23 26
7
26 29
Total =
frec. Re. Acu.
0.08
0.12
0.2
0.44
0.64
0.8
1
Histograma de frecuencia absoluta
14
12
12
Frecuencia absoluta
10
10
10
8
8
6
4
4
4
2
2
0
1
2
3
4
5
6
7
Intervalo de clase
Histograma de frecuencia relativa
0.3
0.24
Frecuencia relativa
0.25
0.2
0.2
0.2
0.16
0.15
0.1
0.08
0.08
0.04
0.05
0
1
2
3
4
5
6
7
Intervalo de clase
Histograma de frecuencia relativa acumulada
1.2
Frecuencia relativa acumulada
1
1
0.8
0.8
0.64
0.6
0.44
0.4
0.2
0.2
0.08
0.12
0
1
2
3
4
Intervalo de clase
5
6
7
2. Dado los datos de precipitación anual, en mm. De la Estación Ayaviri, para el periodo 19592008. Calcular su media, varianza, desviación estándar, coeficiente de variación, coeficiente
de sesgo y coeficiente de curtosis.
año
1959
1960
1961
1962
1963
1964
1965
1966
1967
pp
(mm)
650.00
752,00
536,00
777,00
127,00
505,00
499,00
552,00
701,00
año
1969
1970
1971
1972
1973
1974
1975
1976
1977
pp
(mm)
158,00
81,00
793,00
635,00
279,00
251,00
354,00
494,00
770,00
año
1979
1980
1981
1982
1983
1984
1985
1986
1987
pp
(mm)
139,00
686,00
531,00
105,00
369,00
519,00
515,00
316,00
79,00
año
1989
1990
1991
1992
1993
1994
1995
1996
1997
pp
(mm)
155,00
601,00
149,00
485,00
193,00
724,00
404,00
514,00
608,00
1968 156,00 1978 726,00 1988 211,00 1998 75,00
año
1999
2000
2001
2002
2003
2004
2005
2006
2007
pp
(mm)
239,00
512,00
97,00
370,00
545,00
751,00
460,00
798,00
124,00
2008 416,00
Solución problema 2
Media
Varianza
Desvest
CV
Coef Sesgo
Curtosis
429.72
54181.88
232.77
54.17
-0.06
-1.29
3. Los gastos máximos anuales registrados en la estación hidrométrica Las Perlas en el
Coatzacoalas se muestran en la tabla siguiente:
a) ¿Cuál es la probabilidad de que, en un año cualquiera, el gasto sea mayor o igual a 7500
m3/s?
b) Se planea construir cerca de este sitio un bordo para protección contra inundaciones.
¿Cual debe ser el gasto de diseño si se desea que el periodo de retorno sea de 60 años?
Supóngase que los datos de la tabla siguen una distribución normal.
Resolver usando las funciones de distribución:
Distribución Lognormal
Distribución Pearson III o Gamma de tres parámetros, y
Distribución Gumbel
año
1954
1955
1956
1957
1958
m3/s
2500
3220
2246
1804
2737
año
1959
1960
1961
1962
1963
m3/s
2070
3682
4240
2367
7061
año
1964
1965
1966
1967
1968
m3/s
2489
2350
3706
2675
6267
año
1969
1970
1971
1972
1973
m3/s
5971
4744
6000
4060
6900
año
1974
1975
1976
1977
1978
m3/s
5565
3130
2414
1796
7430
Solución a) Distribución Normal
Media
Desvest
x
Z
F(x)=P(X<7500)=
P(X>7500)
P(X>x)
P(X<x)
F(z)
z=
x (gasto de diseño m3/s) =
3886.16
1825.91
7500
1.9792
0.9761
0.0239
0.0167
0.9833
0.9833
2.1280
7771.7717
b) Distribución Lognormal
P(X>x)
P(X<x)
F(z)
z=
ln(x) =
x=
0.0167
0.9833
0.9833
2.1280
9.1221
9155.0451
Gamma
bheta1
alpha1
delta1
P(X>x)
gl
2y
y
x
0.6778
8.7057
618.8364
-1501.2647
0.0167
17
31.6415
15.8208
8289.2060
alpha
beta
T
x
0.00059773
2997.96706
60
9833.7448
Distribución Pearson III
Distribución Gumbel
4. Dada la serie histórica de descargas medias (m3/s) del rio Huancané, para el periodo 19592008. Realizar las pruebas de bondad de ajustes de Chi-cuadrado (X2 ) y SmirnovKolmogorov, para ver si se ajustan a una distribución normal.
AÑO Q=m3/s AÑO Q=m3/s AÑO Q=m3/s AÑO Q=m3/s AÑO Q=m3/s
1959
1960
1961
1962
1963
1964
1965
1966
1967
28.00
21,00
13,00
28,00
29,00
23,00
29,00
20,00
19,00
1968 26,00
1969
1970
1971
1972
1973
1974
1975
1976
1977
17,00
11,00
14,00
28,00
28,00
21,00
16,00
7,00
28,00
1978 9,00
1979
1980
1981
1982
1983
1984
1985
1986
1987
24,00
21,00
18,00
20,00
19,00
16,00
21,00
7,00
21,00
1988 8,00
1989
1990
1991
1992
1993
1994
1995
1996
1997
14,00
29,00
24,00
23,00
24,00
15,00
27,00
19,00
26,00
1998 23,00
1999
2000
2001
2002
2003
2004
2005
2006
2007
23,00
10,00
14,00
23,00
25,00
27,00
17,00
28,00
26,00
2008 16,00
5. Se desea saber si en una cierta región el gasto máximo medio anual, el área de la cuenca y la
altura media de precipitación máxima en 24 horas se pueden correlacionar linealmente, y que
tan bueno es el ajuste. Los datos se presentan en la tabla siguiente:
Estación
Meteorológic
a
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Y=gasto máx. medio
anual
102 m3/s
45.2
9.1
48.3
35.8
74.9
26.7
12.1
6.8
69.7
57.0
33.7
71.4
88.2
26.6
16.0
X1=área de la
cuenca,
103 km2
1.23
5.25
8.55
7.99
7.36
5.78
5.98
8.11
2.23
6.77
7.02
3.04
6.78
1.23
2.22
Estadísticas de la regresión
Coeficiente de correlación múltiple
Coeficiente de determinación R^2
R^2 ajustado
Error típico
Observaciones
X2=altura media de pp.
máx.
En 24 h. cm
2.9
1.8
2.2
1.1
3.9
2.7
2.5
2.3
2.8
1.1
2.1
3.9
3.2
3.3
2.7
0.4618
0.2132
0.0821
25.0735
15.0000
F. de V.
Regresión
Residuos
Total
Intercepción
Variable X 1
Variable X 2
GL
2
12
14
SC
2044.4866
7544.1667
9588.6533
Coeficientes
-11.5288
2.2847
15.9144
CM
1022.243
628.6806
Error típico
32.9915
2.8637
8.8250
Fc
1.6260
Estadístico t
-0.3494
0.7978
1.8033
Y = - 11.5288 + 2.2847 X1 + 15.9144 X2
PROGRAMA DE SAS 9.2
data regresion;
input X1 X2 Y;
CARDS;
1.23 2.9 45.2
5.25 1.8 9.1
8.55 2.2 48.3
7.99 1.1 35.8
7.36 3.9 74.9
5.78 2.7 26.7
5.98 2.5 12.1
8.11 2.3 6.8
2.23 2.8 69.7
6.77 1.1 57
7.02 2.1 33.7
3.04 3.9 71.4
6.78 3.2 88.2
1.23 3.3 26.6
2.22 2.7 16
PROC PRINT;
PROC REG;
MODEL Y=X1 X2;
PROC GLM;
PROC PLOT;
RUN;
Obs
1
2
3
4
5
6
7
X1
1.23
5.25
8.55
7.99
7.36
5.78
5.98
X2
2.9
1.8
2.2
1.1
3.9
2.7
2.5
Y
45.2
9.1
48.3
35.8
74.9
26.7
12.1
Valor crít de F
0.2372
Probabilidad
0.7328
0.4405
0.0965
8
9
10
11
12
13
14
15
8.11
2.3
6.8
2.23
2.8
69.7
6.77
1.1
57.0
7.02
2.1
33.7
3.04
3.9
71.4
6.78
3.2
88.2
1.23
3.3
26.6
2.22
2.7
16.0
The REG Procedure
Model: MODEL1
Dependent Variable: Y
Analysis of Variance
Source
Model
Error
Corrected Total
Sum of
Squares
2044.48663
7544.16670
9588.65333
DF
2
12
14
Mean
Square
1022.24332
628.68056
F Value
1.63
Root MSE
Dependent Mean
Coeff Var
25.07350
R-Square
41.43333
Adj R-Sq
60.51529
Parameter Estimates
Parameter
Standard
Variable
Intercept
X1
X2
DF
1
1
1
Estimate
-11.52882
2.28473
15.91441
Error
32.99154
2.86373
8.82500
t Value
-0.35
0.80
1.80
Pr > F
0.2372
0.2132
0.0821
Pr > |t|
0.7328
0.4405
0.0965
Y = - 11.5288 + 2.2847 X1 + 15.9144 X2
6. Se realizaron siete (07) pruebas de la resistencia a la compresión en cuatro muestras de
concreto. La fuerza que fractura cada muestra de forma cilíndrica, medida en kilogramos,
está dada en la siguiente tabla:
Muestras
Pruebas
m1
m2
m3
m4
Prueba 1
45
42
43
48
Prueba 2
90
100
102
104
Prueba 3
40
45
56
58
Prueba 4
89
25
98
25
Prueba 5
105
125
87
103
Prueba 6
111
121
120
109
Prueba 7
80
85
86
88
Pruebe con un nivel de significancia de 0.01 si estas muestras son diferentes en su resistencia a
la compresión, y efectuar la prueba de rango múltiple de Duncan a la probabilidad de 0.01.
SOLUCIONARIO MANUAL
1) Hipótesis
H0: µ i=0
Ha:µ i≠ 0
2) Nivel de significación
α = 0.05 y 0.01
3) Estadística de Prueba
Fc=(CMtratam/CMerror)
4) Regla de decisión
Si Fc ≤ F0.05, no se rechaza la Ho. Se representa (NS)
Si F0.05< Fc < F0.01, se rechaza la H0, representando con un asterisco (*)
Si Fc > F0.01; se rechaza la H0, representándose por dos asteriscos (**)
5) Cálculos
..
=
= ×
a) "..#
×
=
×
177603.571
b) = ∑ ∑ −
= $45' + ⋯ + $88' −177603.571
= 202998.000 − 177603.571 = 25394.42857
c) . =
∑
23 .
..
− ×
=
$34' 5⋯5$6'
− = 36. 47
.
d) = ∑
3 ∑83 8 − = 76. 47 −19424.42857
=5970.0000
6) Análisis de varianza
Cuadro 44. Análisis de varianza de los resultados
F.de V.
Pruebas
Error
Total
GL
SC
CM
Fc
19424.42857 3237.40476 11.3878559
5970.00000 284.285714
25394.42857
6
21
27
Ft
2.57
Pr>F
1.109E-05
Niv. Sig.
**
C.V. = 21.1705 %
SOLUCIONARIO CON EL PAQUETE DEL SISTEMA PARA EL ANALISIS
ESTADISTICO
data trabajo;
input x$ y@@;
datalines;
p1 45
p1 42
p1 43
p148
p2
p2
p2
p2
90
100
102
104
p3
p3
p3
p3
40
45
56
58
p4
p4
p4
p4
89
25
98
25
p5
p5
p5
p5
105
125
87
103
p6
p6
p6
p6
proc print;
proc anova;
class x;
model y=x;
means x/duncan alpha=0.01;
run;
RESULTADOS UTILIZANDO EL SAS
Obs
1
2
3
4
x
p1
p2
p3
p4
y
45
90
40
89
111
121
120
109
p7
p7
p7
p7
80
85
86
88
Class
x
5
p5
105
6
p6
111
7
p7
80
8
p1
42
9
p2
100
10
p3
45
11
p4
25
12
p5
125
13
p6
121
14
p7
85
15
p1
43
16
p2
102
17
p3
56
18
p4
98
19
p5
87
20
p6
120
21
p7
86
22
p1
48
23
p2
104
24
p3
58
25
p4
25
26
p5
103
27
p6
109
28
p7
88
The ANOVA Procedure
Class Level Information
Levels
Values
7
p1 p2 p3 p4 p5 p6 p7
Number of observations
28
The ANOVA Procedure
Dependent Variable: y
Source
Model
Error
Corrected Total
DF
6
21
27
Sum of
Squares
Mean Square
19424.42857
3237.40476
5970.00000
284.28571
25394.42857
F Value
11.39
Pr > F
<.0001
R-Square
0.764909
DF
6
Coeff Var
Root MSE
y Mean
21.17048
16.86077
79.64286
Source
Anova SS
Mean Square
F Value
Pr > F
x
19424.42857
3237.40476
11.39
<.0001
The ANOVA Procedure
Duncan's Multiple Range Test for y
NOTE: This test controls the Type I comparisonwise error rate, not the experimentwise
error rate.
Alpha
0.01
Error Degrees of Freedom
21
Error Mean Square
284.2857
Number of Means
2
3
4
5
6
Critical Range
33.76
35.21
36.17
36.87
37.41
Means with the same letter are not significantly different.
Duncan Grouping
Mean
N
x
A
115.25
4
p6
A
105.00
4
p5
A
99.00
4
p2
B
A
84.75
4
p7
B
C
59.25
4
p4
B
C
49.75
4
p3
C
44.50
4
p1
7
37.85
7. Se diseñó un experimento para estudiar el rendimiento de seis (06) detergentes
diferentes. Las siguientes lecturas de “blancura” se obtuvieron con un equipo
especialmente diseñado para 24 cargas de lavado distribuidas en cuatro (04)
modelos de lavadoras:
Detergente
Lavad 1
Lavad 2
Lavad 3
Lavad 4
Detergente A
100
102
101
104
Detergente B
25
46
52
55
Detergente C
45
58
62
66
Detergente D
47
50
63
65
Detergente E
49
54
68
67
Detergente F
99
95
98
99
Considerando los detergentes como tratamientos y las lavadoras como bloques,
efectuar el análisis de variancia y su prueba con un nivel de significación de 0.05 si
existen diferencias entre los detergentes y entre las lavadoras. Además, efectuar la
prueba de Rango Múltiple de Tukey a la probabilidad de 0.05.
Cuadro 45. Análisis de varianza
F. de V.
bloque
tratamiento
error
total
GL
3
5
15
23
SC
CM
Fc
849.5000 283.166667 8.78490176
11506.8333 2301.36667 71.3971044
483.5000 32.2333333
12839.8333
Ft
Sig
SOLUCIONARIO UTILIZANDO EL SISTEMA PARA ANALISIS ESTADISTICO (SAS)
RESULTADO UTILIZANDO EL SAS
data detergente;
input lavadoras detergente rdto;
cards;
1
1
100
1
2
25
1
3
45
1
4
47
1
5
49
1
6
99
2
1
102
2
2
46
2
3
58
2
4
50
2
5
54
2
6
95
3
1
101
3
2
52
3
3
62
3
4
63
3
5
68
3
6
98
4
1
104
4
2
55
4
3
66
4
4
65
4
5
67
4
6
99
proc print;
proc anova;
class lavadoras detergente;
model rdto= lavadoras detergente;
means detergente/tukey alpha =0.05;
run;
Obs
lavadoras
detergente
rdto
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
1
1
100
1
2
25
1
3
45
1
4
47
1
5
49
1
6
99
2
1
102
2
2
46
2
3
58
2
4
50
2
5
54
2
6
95
3
1
101
3
2
52
3
3
62
3
4
63
3
5
68
3
6
98
4
1
104
4
2
55
4
3
66
4
4
65
4
5
67
4
6
99
The ANOVA Procedure
Class Level Information
Class
Levels
Values
lavadoras
4
1 2 3 4
detergente
6
1 2 3 4 5 6
Number of observations
24
The ANOVA Procedure
Dependent Variable: rdto
Source
Model
Error
Corrected Total
Source
lavadoras
detergente
DF
8
15
23
R-Square
0.962344
DF
3
5
Sum of
Squares
Mean Square
F Value
12356.33333
1544.54167
47.92
483.50000
32.23333
12839.83333
Coeff Var
Root MSE
rdto Mean
8.159196
5.677441
69.58333
Anova SS
Mean Square
F Value
849.50000
283.16667
8.78
11506.83333
2301.36667
71.40
Pr > F
<.0001
Pr > F
0.0013
<.0001
Tukey's Studentized Range (HSD) Test for rdto
NOTE: This test controls the Type I experimentwise error rate, but it generally has a
higher Type II
error rate than REGWQ.
Alpha
0.05
Error Degrees of Freedom
15
Error Mean Square
32.23333
Critical Value of Studentized Range 4.59474
Minimum Significant Difference
13.043
Means with the same letter are not significantly different.
Tukey Grouping
Mean
N detergente
A
101.750
4
1
A
97.750
4
6
B
59.500
4
5
B
57.750
4
3
C
B
56.250
4
4
C
44.500
4
2
8. Evaluar el sistema de riego por exudación utilizando cuatro variedades de melón, bajo
modalidad de siembra, SIMPLE HILERA. Se desea probar el comportamiento de tres
variedades híbridas de melón y uno estándar:
V1 : Híbrido Mission
V3 : Híbrido Topfligth.
V2 : Híbrido Mark.
V4 : Híbrido Hales Best Jumbo.
Hipótesis : Ho : Efecto de variedades de melón en estudio es nulo.
H1 : Al menos dos variedades tienen efectos distintos.
Datos: Rendimiento en Kg. por parcela.
C1
C2
C3
C4
F1
36V1
50 V2
43 V3
35 V4
F2
29 V4
53 V3
41 V2
63 V1
F3
37 V2
41 V4
41 V1
63 V3
F4
38 V3
40 V1
35 V4
41 V2
F. de V.
Hilera
Columna
Tratamiento
Error
Total
GL
3
3
3
6
15
SC
CM
170.75
56.92
552.75
184.25
430.25
143.417
254.0000 42.3333
1407.7500
Fc
1.3445
4.3524
3.3878
Ft
sig.
SOLUCIONARIO APLICANDO EL SAS DISEÑO DE CUADRADO LATINO
DATA OCHO;
INPUT FILA COLUMNA TRAT $ RDTO;
CARDS;
1
1
V1
36
1
2
V2
50
1
3
V3
43
1
4
V4
35
2
1
V4
29
2
2
V3
53
2
3
V2
41
2
4
V1
63
3
1
V2
37
3
2
V4
41
3
3
V1
41
3
4
V3
63
4
1
V3
38
4
2
V1
40
4
3
V4
35
4
4
V2
41
PROC PRINT;
PROC ANOVA;
CLASS FILA COLUMNA TRAT;
MODEL RDTO= FILA COLUMNA TRAT;
MEANS FILA COLUMNA TRAT/DUNCAN;
RUN;
RESULTADOS UTILIZANDO EL SAS
Obs
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
FILA
COLUMNA
TRAT
RDTO
1
1
V1
36
1
2
V2
50
1
3
V3
43
1
4
V4
35
2
1
V4
29
2
2
V3
53
2
3
V2
41
2
4
V1
63
3
1
V2
37
3
2
V4
41
3
3
V1
41
3
4
V3
63
4
1
V3
38
4
2
V1
40
4
3
V4
35
4
4
V2
41
The ANOVA Procedure
Class Level Information
Class
Levels
Values
FILA
4
1 2 3 4
COLUMNA
4
1 2 3 4
TRAT
4
V1 V2 V3 V4
Number of observations
16
The ANOVA Procedure
Dependent Variable: RDTO
Source
Model
Error
Corrected Total
DF
9
6
15
Sum of
Squares
Mean Square
1153.750000
128.194444
254.000000
42.333333
1407.750000
F Value
3.03
Pr > F
0.0954
R-Square
0.819570
Source
FILA
COLUMNA
TRAT
DF
3
3
3
Coeff Var
15.17529
Anova SS
170.7500000
552.7500000
430.2500000
Root MSE
6.506407
Mean Square
56.9166667
184.2500000
143.4166667
RDTO Mean
42.87500
F Value
1.34
4.35
3.39
Pr > F
0.3456
0.0596
0.0949
Duncan's Multiple Range Test for RDTO
NOTE: This test controls the Type I comparisonwise error rate, not the experimentwise
error rate.
Alpha
0.05
Error Degrees of Freedom
6
Error Mean Square
42.33333
Number of Means
2
3
4
Critical Range
11.26
11.67
11.87
Means with the same letter are not significantly different.
Duncan Grouping
Mean
N
FILA
A
46.500
4
2
A
45.500
4
3
A
41.000
4
1
A
38.500
4
4
The ANOVA Procedure
Duncan's Multiple Range Test for RDTO
NOTE: This test controls the Type I comparisonwise error rate, not the experimentwise
error rate.
Alpha
0.05
Error Degrees of Freedom
6
Error Mean Square
42.33333
Number of Means
2
3
4
Critical Range
11.26
11.67
11.87
Means with the same letter are not significantly different.
Duncan Grouping
Mean
N
COLUMNA
A
50.500
4
4
B
A
46.000
4
2
B
A
40.000
4
3
B
35.000
4
1
The ANOVA Procedure
Duncan's Multiple Range Test for RDTO
NOTE: This test controls the Type I comparisonwise error rate, not the experimentwise
error rate.
Alpha
0.05
Error Degrees of Freedom
6
Error Mean Square
42.33333
Number of Means
2
3
4
Critical Range
11.26
11.67
11.87
Means with the same letter are not significantly different.
Duncan Grouping
Mean
N
TRAT
A
49.250
4
V3
B
A
45.000
4
V1
B
A
42.250
4
V2
B
35.000
4
V4
9. Supóngase que se efectúan dos repeticiones del experimento de soldadura, empleando el
cuadrado latino, los resultados que señalan el número de libras fuerza de tensión requerida
para separar los puntos soldados, fueron como se indica a continuación:
REPETICIÓN I
Fundentes
F1
F2
F3
F4
A 20.0
B 17.5
C 14.0
D 14.0
D 24.0
A 21.0
B 18.0
C 14.1
C 12.0
D 18.0
A 23.0
B 19.0
B 20.0
C 15.0
D 13.0
A 22.0
REPETICIÓN II
Fundentes
F1
F2
F3
F4
C 12.0
D 10.0
A 24.2
B 22.1
B 19.5
C 13.0
D 10.5
A 22.3
A 23.5
B 17.2
C 20.4
D 14.0
D 11.0
A 22.2
B 20.5
C 14.5
Analice el experimento como un cuadrado latino y pruébese con un nivel de significancia de
0.05 si existen diferencias en los métodos (A, B, C y D), en los operadores (filas), los fundentes
(columnas) y, entre las producciones. Utilizar la prueba de rango múltiple de Tukey α = 0.01, si
es que es significativo.
F. de V.
Pr > F
GL
SC
CM
Fc
Sig
repetición
1
1.8528125
1.8528
0.181683
NS
0.6742
hilera
3
12.1609375
4.0536
0.3974922
NS
0.7562
columna
3
7.2009375
2.4003
0.2353697
NS
0.8707
tratamiento
error
Total
3
21
31
365.545937
214.159062
600.919688
121.85
10.198
11.948229
**
SOLUCIONARIO MEDIANTE EL SAS
data fundente;
input repet hilera columna trat$
cards;
1
1
1
1
1
1
1
1
1
2
1
2
1
2
1
2
1
2
3
4
1
2
3
4
A
B
C
D
D
A
B
C
20
17.5
14
14
24
21
18
14.1
rdto;
0.0001
1
3
1
C
12
1
3
2
D
18
1
3
3
A
23
1
3
4
B
19
1
4
1
B
20
1
4
2
C
15
1
4
3
D
13
1
4
4
A
22
2
1
1
C
12
2
1
2
D
10
2
1
3
A
24.2
2
1
4
B
22.1
2
2
1
B
19.5
2
2
2
C
13
2
2
3
D
10.5
2
2
4
A
22.3
2
3
1
A
23.5
2
3
2
B
17.2
2
3
3
C
20.4
2
3
4
D
14
2
4
1
D
11
2
4
2
A
22.2
2
4
3
B
20.5
2
4
4
C
14.5
PROC PRINT;
PROC ANOVA;
CLASS REPET HILERA COLUMNA TRAT;
MODEL RDTO= REPET HILERA COLUMNA TRAT;
MEANS HILERA COLUMNA TRAT/TUKEY ALPHA=0.01;
RUN;
RESULTADOS DEL PROGRAMA DE SAS
Obs
repet
hilera
columna
trat
rdto
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
2
2
2
1
1
1
1
2
2
2
2
3
3
3
3
4
4
4
4
1
1
1
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
A
B
C
D
D
A
B
C
C
D
A
B
B
C
D
A
C
D
A
20.0
17.5
14.0
14.0
24.0
21.0
18.0
14.1
12.0
18.0
23.0
19.0
20.0
15.0
13.0
22.0
12.0
10.0
24.2
20
21
22
23
24
25
26
27
28
29
30
31
32
2
2
2
2
2
2
2
2
2
2
2
2
2
1
4
B
22.1
2
1
B
19.5
2
2
C
13.0
2
3
D
10.5
2
4
A
22.3
3
1
A
23.5
3
2
B
17.2
3
3
C
20.4
3
4
D
14.0
4
1
D
11.0
4
2
A
22.2
4
3
B
20.5
4
4
C
14.5
The ANOVA Procedure
Class Level Information
Class
Levels
Values
repet
2
1 2
hilera
4
1 2 3 4
columna
4
1 2 3 4
trat
4
A B C D
Number of observations
32
Dependent Variable: rdto
Sum of
Source
DF
Squares
Mean Square
F Value
Pr > F
Model
10
386.7606250
38.6760625
3.79
0.0048
Error
21
214.1590625
10.1980506
Corrected Total
31
600.9196875
R-Square
Coeff Var
Root MSE
rdto Mean
0.643615
18.19947
3.193439
17.54688
Source
DF
Anova SS
Mean Square
F Value
Pr > F
repet
1
1.8528125
1.8528125
0.18
0.6743
hilera
3
12.1609375
4.0536458
0.40
0.7562
columna
3
7.2009375
2.4003125
0.24
0.8707
trat
3
365.5459375
121.8486458
11.95
<.0001
Tukey's Studentized Range (HSD) Test for rdto
NOTE: This test controls the Type I experimentwise error rate, but it generally has a
higher Type II
error rate than REGWQ.
Alpha
0.01
Error Degrees of Freedom
21
Error Mean Square
10.19805
Critical Value of Studentized Range 4.98557
Minimum Significant Difference
5.629
Means with the same letter are not significantly different.
Tukey Grouping
Mean
N
hilera
A
18.388
8
3
A
17.800
8
2
A
17.275
8
4
A
16.725
8
1
Tukey's Studentized Range (HSD) Test for rdto
NOTE: This test controls the Type I experimentwise error rate, but it generally has a
higher Type II
error rate than REGWQ.
Alpha
0.01
Error Degrees of Freedom
21
Error Mean Square
10.19805
Critical Value of Studentized Range 4.98557
Minimum Significant Difference
5.629
Means with the same letter are not significantly different.
Tukey Grouping
Mean
N
columna
A
17.950
8
3
A
17.750
8
4
A
17.750
8
1
A
16.738
8
2
Tukey's Studentized Range (HSD) Test for rdto
NOTE: This test controls the Type I experimentwise error rate, but it generally has a
higher Type II
error rate than REGWQ.
Alpha
0.01
Error Degrees of Freedom
21
Error Mean Square
10.19805
Critical Value of Studentized Range 4.98557
Minimum Significant Difference
5.629
Means with the same letter are not significantly different.
Tukey Grouping
Mean
N
trat
A
22.275
8
A
B
A
19.225
8
B
B
14.375
8
C
B
14.313
8
D
10. Se desea determinar los efectos de la temperatura de la caldera (1600 y 1900 °F) y del
ancho del horno
(4, 8 y 12 pulgadas) para el experimento; supóngase que cinco
repeticiones de ese experimento dan los siguientes tiempos requeridos para la producción
del coque (en horas):
A
A(4) Pulgadas
A(8) Pulgadas
A(12) Pulgadas
T
T1=1600
T2=1900
T1=1600
T2=1900
T1=1600
T2=1900
I
12.5
8.2
17.1
5.2
17.8
7.6
II
14.0
9.3
16.9
4.6
15.6
9.1
III
12.7
6.4
17.5
8.8
17.8
7.9
IV
13.5
7.8
17.3
5.9
16.8
8.1
V
14.4
10.7
20.2
8.3
22.4
10.2
Explíquese un análisis de variancia basado en este experimento con dos factores y pruébese la
significancia de los efectos factoriales, empleando un nivel de significancia de 0.05. Aplicar la
prueba de Duncan α = 0.05, si es que es significativo al nivel de ANOVA.
RESULTADO UTILIZANDO EL PAQUETE DE SISTEMA DE ANALISIS ESTADISTICO
data flores;
input ancho temp hr;
cards;
1
1
12.5
1
1
14
1
1
12.7
1
1
13.5
1
1
14.4
1
2
8.2
1
2
9.3
1
2
6.4
1
2
7.8
1
2
10.7
2
1
17.1
2
1
16.9
2
1
17.5
2
1
17.3
2
1
20.2
2
2
5.2
2
2
4.6
2
2
8.8
2
2
5.9
2
2
8.3
3
1
17.8
3
1
15.6
3
1
17.8
3
1
16.8
3
1
22.4
3
2
7.6
3
2
9.1
3
2
7.9
3
2
8.1
3
2
10.2
proc print;
proc anova;
class ancho temp;
model hr=ancho temp ancho*temp;
means ancho temp ancho*temp/duncan;
run;
RESULTADO
Obs
ancho
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
temp
hr
1
1
12.5
1
1
14.0
1
1
12.7
1
1
13.5
1
1
14.4
1
2
8.2
1
2
9.3
1
2
6.4
1
2
7.8
1
2
10.7
2
1
17.1
2
1
16.9
2
1
17.5
2
1
17.3
2
1
20.2
2
2
5.2
2
2
4.6
2
2
8.8
2
2
5.9
2
2
8.3
3
1
17.8
3
1
15.6
3
1
17.8
3
1
16.8
3
1
22.4
3
2
7.6
3
2
9.1
3
2
7.9
3
2
8.1
3
2
10.2
The ANOVA Procedure
Class Level Information
Class
Levels
Values
ancho
3
1 2 3
temp
2
1 2
Source
Model
Error
Corrected Total
Source
ancho
temp
ancho*temp
Number of observations
30
The ANOVA Procedure
Dependent Variable: hr
Sum of
DF
Squares
Mean Square
5
630.8106667
126.1621333
24
65.8640000
2.7443333
29
696.6746667
R-Square
Coeff Var
Root MSE
0.905459
13.63085
1.656603
DF
Anova SS
Mean Square
2
28.3326667
14.1663333
1
549.5520000
549.5520000
2
52.9260000
26.4630000
F Value
45.97
Pr > F
<.0001
hr Mean
12.15333
F Value
5.16
200.25
9.64
Pr > F
0.0137
<.0001
0.0008
The ANOVA Procedure
Duncan's Multiple Range Test for hr
NOTE: This test controls the Type I comparisonwise error rate, not the experimentwise
error rate.
Alpha
0.05
Error Degrees of Freedom
24
Error Mean Square
2.744333
Number of Means
2
3
Critical Range
1.529
1.606
Means with the same letter are not significantly different.
Duncan Grouping
Mean
N
ancho
A
13.3300
10
3
B
A
12.1800
10
2
B
10.9500
10
1
Duncan's Multiple Range Test for hr
NOTE: This test controls the Type I comparisonwise error rate, not the experimentwise
error rate.
Alpha
0.05
Error Degrees of Freedom
24
Error Mean Square
2.744333
Number of Means
2
Critical Range
1.248
Means with the same letter are not significantly different.
Duncan Grouping
Mean
N
temp
A
16.4333
15
1
B
7.8733
15
2
The ANOVA Procedure
Level of
Level of
--------------hr------------ancho
temp
N
Mean
Std Dev
1
1
5
13.4200000
0.81670068
1
2
5
8.4800000
1.61771444
2
1
5
17.8000000
1.36014705
2
2
5
6.5600000
1.88228584
3
1
5
18.0800000
2.57914715
3
2
5
8.5800000
1.06630202
11. En un centro de investigación en trigo, se llevó a cabo un experimento para estudiar 06
variedades (A, B, C, D, E y F), y debido a la conformación del terreno, se utilizó el diseño
de cuadrado latino, el rendimiento del trigo expresado en Kg/parcela.
A 21
B 20
C 12
D 23
E 16
F 30
B 22
C 16
D 21
E 18
F 29
A 14
C 16
D 20
E 20
F 31
A 13
B 24
D 28
E 21
F 32
A 12
B 26
C 18
E 20
F 33
A 13
B 28
C 15
D 27
F 31
A 16
B 27
C 14
D 25
E 23
Efectuar el análisis de variancia correspondiente y efectuar la prueba de significancia de Tukey
a la probabilidad de 0.05
SOLUCIONARIO CON EL SISTEMA DE ANALISIS ESTADISTICO
DATA LATINO;
INPUT HILERA COLUMNA TRATAM$ RDTO;
CARDS;
1
1
A
21
1
2
B
20
1
3
C
12
1
4
D
23
1
5
E
16
1
6
F
30
2
1
B
22
2
2
C
16
2
3
D
21
2
4
E
18
2
5
F
29
2
6
A
14
3
1
C
16
3
2
D
20
3
3
E
20
3
4
F
31
3
5
A
13
3
6
B
24
4
1
D
28
4
2
E
21
4
3
F
32
4
4
A
12
4
5
B
26
4
6
C
18
5
1
E
20
5
2
F
33
5
3
A
13
5
4
B
28
5
5
C
15
5
6
D
27
6
1
F
31
6
2
A
16
6
3
B
27
6
4
C
14
6
5
D
25
6
6
E
23
PROC PRINT;
PROC ANOVA;
CLASS HILERA COLUMNA TRATAM;
MODEL RDTO=HILERA COLUMNA TRATAM;
MEANS HILERA COLUMNA TRATAM/TUKEY; RUN;
RESULTADO MEDIANTE EL ANALISIS ESTADISTICO
Obs
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
HILERA
COLUMNA
TRATAM
RDTO
1
1
A
21
1
2
B
20
1
3
C
12
1
4
D
23
1
5
E
16
1
6
F
30
2
1
B
22
2
2
C
16
2
3
D
21
2
4
E
18
2
5
F
29
2
6
A
14
3
1
C
16
3
2
D
20
3
3
E
20
3
4
F
31
3
5
A
13
3
6
B
24
4
1
D
28
4
2
E
21
4
3
F
32
4
4
A
12
4
5
B
26
4
6
C
18
5
1
E
20
5
2
F
33
5
3
A
13
5
4
B
28
5
5
C
15
5
6
D
27
6
1
F
31
6
2
A
16
6
3
B
27
6
4
C
14
6
5
D
25
6
6
E
23
The ANOVA Procedure
Class Level Information
Class
Levels
Values
HILERA
6
1 2 3 4 5 6
COLUMNA
6
1 2 3 4 5 6
TRATAM
6
A B C D E F
Number of observations
36
The ANOVA Procedure
Dependent Variable: RDTO
Sum of
Source
DF
Squares
Mean Square
F Value
Pr > F
Model
15
1244.750000
82.983333
12.74
<.0001
Error
20
130.222222
6.511111
Corrected Total
35
1374.972222
R-Square
Coeff Var
Root MSE
RDTO Mean
0.905291
11.85300
2.551688
21.52778
Source
DF
Anova SS
Mean Square
F Value
Pr > F
HILERA
5
52.805556
10.561111
1.62
0.1999
COLUMNA
5
31.472222
6.294444
0.97
0.4615
TRATAM
5
1160.472222
232.094444
35.65
<.0001
Tukey's Studentized Range (HSD) Test for RDTO
NOTE: This test controls the Type I experimentwise error rate, but it generally has a
higher Type II
error rate than REGWQ.
Alpha
0.05
Error Degrees of Freedom
20.00
Error Mean Square
6.51
Critical Value of Studentized Range
4.44
Minimum Significant Difference
4.63
Means with the same letter are not significantly different.
Tukey Grouping
Mean
N
HILERA
A
22.833
6
4
A
22.667
6
5
A
22.667
6
6
A
20.667
6
3
A
20.333
6
1
A
20.000
6
2
Tukey's Studentized Range (HSD) Test for RDTO
NOTE: This test controls the Type I experimentwise error rate, but it generally has a
higher Type II
error rate than REGWQ.
Alpha
0.05
Error Degrees of Freedom
20.00
Error Mean Square
6.51
Critical Value of Studentized Range 4.44
Minimum Significant Difference
4.6307
Means with the same letter are not significantly different.
Tukey Grouping
Mean
N
COLUMNA
A
23.000
6
1
A
22.667
6
6
A
21.000
6
4
A
21.000
6
2
A
20.833
6
3
A
20.667
6
5
Tukey's Studentized Range (HSD) Test for RDTO
NOTE: This test controls the Type I experimentwise error rate, but it generally has a
higher Type II
error rate than REGWQ.
Alpha
0.05
Error Degrees of Freedom
20.00
Error Mean Square
6.51
Critical Value of Studentized Range 4.44
Minimum Significant Difference
4.63
Means with the same letter are not significantly different.
Tukey Grouping
Mean
N
TRATAM
A
31.000
6
F
B
24.500
6
B
C
B
24.000
6
D
C
D
19.667
6
E
E
D
15.167
6
C
E
14.833
6
A
12. Aplicando la regresión lineal múltiple, se desea saber si en una cierta región el gasto
máximo medio anual, el área de la cuenca y la altura media de la precipitación máxima en
24 horas se pueden correlacionar linealmente, y que tan bueno es el ajuste. Los datos se
presentan en la tabla siguiente:
Estación
Y = gasto máximo
medio anual, 102m3/s
X1 = área de la
cuenca, 103km2
X2 = altura media de precipitación
máximo. en 24 h. cm
1
20.5
1.25
1.7
2
8.5
0.87
2.1
3
85.5
5.69
1.9
4
105.0
8.27
1.9
5
24.8
1.62
2.1
6
3.8
0.18
2.4
7
1.8
0.15
3.2
8
18.0
1.40
2.7
9
85.5
8.27
2.1
10
105.0
1.62
2.4
data regresion;
input X1 X2 Y;
CARDS;
20.5 1.25 1.7
8.5
0.87 2.1
85.5 5.69 1.9
105
8.27 1.9
24.8 1.62 2.1
3.8
0.18 2.4
1.8
0.15 3.2
18
1.4
2.7
85.5 8.27 2.1
105
1.62 2.4
PROC PRINT;
PROC REG;
MODEL Y= X1 X2;
RUN;
Obs
1
2
3
4
5
6
7
8
9
10
Source
Model
Error
Corrected Total
DF
2
7
9
X1
X2
Y
20.5
1.25
1.7
8.5
0.87
2.1
85.5
5.69
1.9
105.0
8.27
1.9
24.8
1.62
2.1
3.8
0.18
2.4
1.8
0.15
3.2
18.0
1.40
2.7
85.5
8.27
2.1
105.0
1.62
2.4
The REG Procedure
Model: MODEL1
Dependent Variable: Y
Analysis of Variance
Sum of
Mean
Squares
Square
F Value
0.40973
0.20487
1.06
1.35527
0.19361
1.76500
Pr > F
0.3967
Root MSE
Dependent Mean
Coeff Var
Variable
Intercept
X1
X2
0.44001
R Square
R-Square
0.2321
2.25000
Adj R-Sq
R Sq
0.0128
19.55605
Parameter Estimates
Parameter
Standard
Estimate
Error
t Value
Pr > |t|
2.45361
0.20877
11.75
<.0001
-0.00064324
0.00542
-0.12
0.12
0.9088
-0.05939
0.07355
-0.
DF
1
1
1
13. Se desea estimar los gastos en alimentación de una familia
en base a la información que
proporcionan las variables regresoras X1 =“ingresos
“ingresos mensuales” y X2 =“número de
miembros de la familia”. Para ello se recoge una muestra aleatoria simple de 15 familias
cuyos resultados son los de la tabla adjunta (El gasto e ingreso está dado en miles de soles).
Efectuar el análisis de regresión múltiple.
Gasto (Y) Ingreso (X1) Tamaño (X2)
35
21
3
31
11
4
32
9
5
46
16
4
125
62
4
44
23
3
52
18
6
29
10
5
129
89
3
35
24
2
35
12
4
78
47
3
43
35
2
47
29
3
38
14
4
Regression Analysis: Y versus X1, X2
The regression equation is
Y = - 18.6 + 1.50 X1 + 8.12 X2
Predictor
Constant
X1
X2
S = 7.64694
Coef
-18.601
1.50326
8.121
SE Coef
8.917
0.09837
1.984
R
R-Sq
= 95.2%
T
-2.09
15.28
4.09
P
0.059
0.000
0.001
VIF
1.2
1.2
R-Sq(adj)
Sq(adj) = 94.4%
Analysis of Variance
Source
Regresión
Residual Error
Total
DF
2
12
14
SS
13847.2
701.7
14548.9
MS
6923.6
58.5
F
118.40
SOLUCIONARIO CON SAS
Obs
X1
X2
Y
P
0.000
1
21
3
35
2
11
4
31
3
9
5
32
4
16
4
46
5
62
4
125
6
23
3
44
7
18
6
52
8
10
5
29
9
89
3
129
10
24
2
35
11
12
4
35
12
47
3
78
13
35
2
43
14
29
3
47
15
14
4
38
The REG Procedure
Model: MODEL1
Dependent Variable: Y
Analysis of Variance
Sum of
Mean
Source
DF
Squares
Square
F Value
Pr > F
Model
2
13847
6923.61222
118.40
<.0001
Error
12
701.70890
58.47574
Corrected Total
14
14549
Root MSE
7.64694
R-Square
0.9518
Dependent Mean
53.26667
Adj R-Sq
0.9437
Coeff Var
14.35596
Parameter Estimates
Parameter
Standard
Variable
DF
Estimate
Error
t Value
Pr > |t|
Intercept
1
-18.60147
8.91730
-2.09
0.0590
X1
1
1.50326
0.09837
15.28
<.0001
X2
1
8.12097
1.98364
4.09 .. 0.0015
Y = - 18.60147 + 1.50326 X1 + 8.12097 X2
NOTA
LOS AUTORES DEL TEXTO DE: METODOS ESTADISTICOS PARA LA
INVESTIGACION ESTAN TRABAJANDO PARA EDITAR UN TEXTO QUE
SERA DE MUCHA UTILIDAD PARA LOS ESTUDIANTES DE PREGRADO Y
POST GRADO DE LA UNIVERSIDAD NACIONAL DEL ALTIPLANO DE
PUNO.
Dr. Eduardo Flores Condori
Dr.(c) M.SC. Eduardo Luis Flores Quispe