Hipótesis Estadística

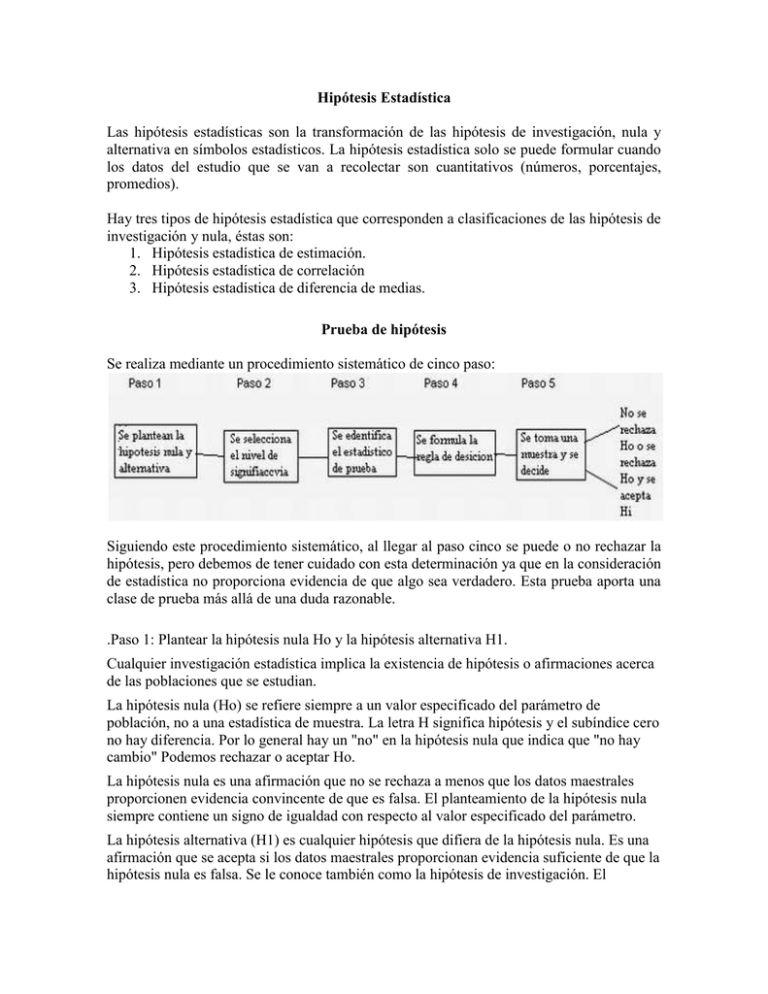
Hipótesis Estadística
Las hipótesis estadísticas son la transformación de las hipótesis de investigación, nula y
alternativa en símbolos estadísticos. La hipótesis estadística solo se puede formular cuando
los datos del estudio que se van a recolectar son cuantitativos (números, porcentajes,
promedios).
Hay tres tipos de hipótesis estadística que corresponden a clasificaciones de las hipótesis de
investigación y nula, éstas son:
1. Hipótesis estadística de estimación.
2. Hipótesis estadística de correlación
3. Hipótesis estadística de diferencia de medias.
Prueba de hipótesis
Se realiza mediante un procedimiento sistemático de cinco paso:
Siguiendo este procedimiento sistemático, al llegar al paso cinco se puede o no rechazar la
hipótesis, pero debemos de tener cuidado con esta determinación ya que en la consideración
de estadística no proporciona evidencia de que algo sea verdadero. Esta prueba aporta una
clase de prueba más allá de una duda razonable.
.Paso 1: Plantear la hipótesis nula Ho y la hipótesis alternativa H1.
Cualquier investigación estadística implica la existencia de hipótesis o afirmaciones acerca
de las poblaciones que se estudian.
La hipótesis nula (Ho) se refiere siempre a un valor especificado del parámetro de
población, no a una estadística de muestra. La letra H significa hipótesis y el subíndice cero
no hay diferencia. Por lo general hay un "no" en la hipótesis nula que indica que "no hay
cambio" Podemos rechazar o aceptar Ho.
La hipótesis nula es una afirmación que no se rechaza a menos que los datos maestrales
proporcionen evidencia convincente de que es falsa. El planteamiento de la hipótesis nula
siempre contiene un signo de igualdad con respecto al valor especificado del parámetro.
La hipótesis alternativa (H1) es cualquier hipótesis que difiera de la hipótesis nula. Es una
afirmación que se acepta si los datos maestrales proporcionan evidencia suficiente de que la
hipótesis nula es falsa. Se le conoce también como la hipótesis de investigación. El
planteamiento de la hipótesis alternativa nunca contiene un signo de igualdad con respecto
al valor especificado del parámetro.
Paso 2: Seleccionar el nivel de significancia.
Nivel de significacia: Probabilidad de rechazar la hipótesis nula cuando es verdadera. Se le
denota mediante la letra griega α, tambiιn es denominada como nivel de riesgo, este
termino es mas adecuado ya que se corre el riesgo de rechazar la hipótesis nula, cuando en
realidad es verdadera. Este nivel esta bajo el control de la persona que realiza la prueba.
Si suponemos que la hipótesis planteada es verdadera, entonces, el nivel de significación
indicará la probabilidad de no aceptarla, es decir, estén fuera de área de aceptación. El nivel
de confianza (1-α), indica la probabilidad de aceptar la hipótesis planteada, cuando es
verdadera en la población.
La distribución de muestreo de la estadística de prueba se divide en dos regiones, una
región de rechazo (conocida como región crítica) y una región de no rechazo (aceptación).
Si la estadística de prueba cae dentro de la región de aceptación, no se puede rechazar la
hipótesis nula.
La región de rechazo puede considerarse como el conjunto de valores de la estadística de
prueba que no tienen posibilidad de presentarse si la hipótesis nula es verdadera. Por otro
lado, estos valores no son tan improbables de presentarse si la hipótesis nula es falsa. El
valor crítico separa la región de no rechazo de la de rechazo.
Tipos de errores
Cualquiera sea la decisión tomada a partir de una prueba de hipótesis, ya sea de aceptación
de la Ho o de la Ha, puede incurrirse en error:
Un error tipo I se presenta si la hipótesis nula Ho es rechazada cuando es verdadera y debía
ser aceptada. La probabilidad de cometer un error tipo I se denomina con la letra alfa α
Un error tipo II, se denota con la letra griega β se presenta si la hipótesis nula es aceptada
cuando de hecho es falsa y debía ser rechazada.
En cualquiera de los dos casos se comete un error al tomar una decisión equivocada.
En la siguiente tabla se muestran las decisiones que pueden tomar el investigador y las
consecuencias posibles.
Para que cualquier ensayode hipótesis sea bueno, debe diseñarse de forma que minimice los
errores de decisión. En la práctica un tipo de error puede tener más importancia que el otro,
y así se tiene a conseguir poner una limitación al error de mayor importancia. La única
forma de reducir ambos tipos de errores es incrementar el tamaño de la muestra, lo cual
puede ser o no ser posible.
HIPOTESIS NULA
Las hipótesis nulas son proposiciones que sirven para refutar o negar lo que afirma la
hipótesis de investigación. Las hipótesis nulas se simbolizan de la siguiente manera Ho
Hay tantas clases de hipótesis nulas como de investigación.
No diferencia, no relación, no efecto.
Ejemplos:
“No hay relación entre la autoestima y el temor de logro”. (Hipótesis nula respecto a una
correlación).
“La percepción en la similitud de religión, creencias y valores no provoca mayor atracción
entre las personas”. (Hipótesis que niega la relación causal).
No hay procedimientos estadísticos disponibles para probar directamente las hipótesis de
investigación. Cuando se quiere realizar una prueba estadística en una investigación
empírica, la hipótesis de investigación se debe trasladar a un tipo de hipótesis conocida
como hipótesis nula (simbolizada como Ho. Se llama nula porque establece que no hay
diferencia, o no hay efecto, o no hay relación. La hipótesis nula declara una negación de lo
que el experimentador espera o predice. El investigador espera demostrar que después del
tratamiento experimental, dos poblaciones tienen diferentes medias, pero la hipótesis nula
establecería que las medias de las poblaciones no son diferentes.
Nivel de significancia:
Al contrastar una cierta hipótesis, la máxima probabilidad con la que estamos dispuestos a
correr el riesgo de cometer un error de tipo I se llama nivel de significancia. Esta
probabilidad se denota por , se suele especificar antes de la muestra, de manera que los
resultados no influyan en nuestra elección.
En la práctica es frecuente un nivel de significancia de 0.05 ó 0.01, si bien se usan otros
valores. Si, por ejemplo, se escoge un nivel de significancia del 5% ó 0.05 al diseñar una
regla de decisión entonces hay unas cinco oportunidades entre cien de rechazar la hipótesis
cuando debiera haberse aceptado; es decir, tenemos un 95% de confianza de que hemos
adoptado la decisión correcta. En tal caso decimos que la hipótesis a sido rechazada al nivel
de significancia 0.05 lo cual quiere decir que la hipótesis tiene una probabilidad del 5% de
ser falsa.
P valor:
Una vez obtenida la muestra, se puede calcular una cantidad que sí que permite resumir el
resultado del experimento de manera objetiva. Esta cantidad es el p-valor que corresponde
al nivel de significación más pequeño posible que puede escogerse, para el cual todavía se
aceptaría la hipótesis alternativa con las observaciones actuales. Cualquier nivel de
significación escogido inferior al p-valor (simbólicamente pv) comporta aceptar H0.
Obviamente, al ser una probabilidad, se cumple que:
0 ≤ pv ≤ 1
El p-valor es una medida directa de lo verosímil que resulta obtener una muestra como la
actual si es cierta H0. Los valores pequeños indican que es muy infrecuente obtener una
muestra como la actual, en cambio, los valores altos que es frecuente. El p-valor se emplea
para indicar cuánto (o cuán poco) contradice la muestra actual la hipótesis alternativa.
Potencia de una prueba:
El complemento de la probabilidad de cometer un error del tipo II se conoce como potencia
de una prueba estadística. La potencia de una prueba es la probabilidad de rechazar la
hipótesis nula cuando de hecho esta es falsa y debería ser rechazada. Una manera en que
podemos controlar la probabilidad de cometer un error del tipo II en un estudio, consiste en
aumentar el tamaño de la muestra.
La Potencia de una prueba β representa la probabilidad de que la hipótesis nula no sea
rechazada cuando de hecho es falsa y debería rechazársele. La potencia de prueba 1-β
representa la sensibilidad de la prueba estadística para detectar cambios que se presentan al
medir la probabilidad de rechazar la hipótesis nula cuando de hecho es falsa y debería ser
rechazada. La potencia de prueba estadística depende de qué tan diferente en realidad es la
media verdadera de la población del valor supuesto. Una prueba de un extremo es más
poderosa que una de dos extremos, y se debería utilizar siempre que sea adecuado
especificar la dirección de la hipótesis alternativa. Puesto que la probabilidad de cometer un
error tipo I y la probabilidad de cometer un error tipo II tienen una relación inversa y esta
última es el complemento de la potencia de prueba (1-β), entonces α y la potencia de la
prueba varían en proporción directa. Un aumento en el valor del nivel de significación
escogido, tendría como resultado un aumento en la potencia y una disminución en α tendría
como resultado una disminución en la potencia. Un aumento en el tamaño de la muestra
escogida tendría como resultado un aumento en la potencia de la prueba, una disminución
en el tamaño de la muestra seleccionada tendría como resultado una disminución en la
potencia.