x - U-Cursos

Universidad de Chile
Departamento de Ingeniería Matemática
0.5
0.4
MA-33A
0.3
0.2
0.1
Capítulo 3:
0
-0.1
-0.2
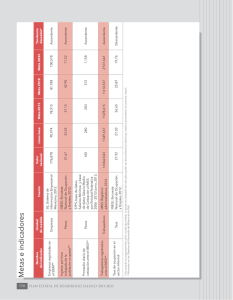
Interpolación y
y=x/(x 2+1)
5th degree
7th degree
9th degree
-0.3
-0.4
-0.5
-5
-4
-3
-2
-1
0
1
2
3
4
5
Aproximación Funciones
Gonzalo Hernández Oliva
GHO
IA - MA-33A
1
Interpolación y Aproximación de
Funciones : Temario
1) Motivación
2) Interpolación de Lagrange, Newton, Hermite
3) Interpolación por Spline Cúbicos
4) Aproximación de Taylor
5) Aproximación por Mínimos Cuadrados:
Discretos y Continuos
6) Interpolación y Aproximación Trigonométrica
GHO
IA - MA-33A
2
Interp. y Aprox. de Funciones:
1) Motivación 1: Interpolación Polinomial
Dados (n+1) puntos ( xi , yi )
Encontrar un polinomio de
grado n tal que:
n
yi = p ( xi ) = ∑ ak xi k
k =0
p(xi ) = yi ∀i =1,..., n +1
yi
x
x
x
x
x
x
x
x
p(x)
x
xi
GHO
IA - MA-33A
3
Interp. y Aprox. de Funciones:
1) Motivación 1: Interpolación Polinomial
yi = p ( xi ) ∀i = 1,..., (n + 1)
n
yi = p ( xi ) = ∑ ak xi
k
k =0
1
x1
x 21

x n1
a0
y1
1
x2
x 22

x n2
a1
y2
1
x3
x 23

x n3
a2







an
y n1
2
 x nn1
1 x n1 x n1
GHO
IA - MA-33A

y3
4
Interp. y Aprox. de Funciones:
1) Motivación 1: Interpolación Polinomial
GHO
IA - MA-33A
5
Interp. y Aprox. de Funciones:
1) Motivación 1: Interpolación por Splines
y
S0 ( x1 ) = S1 ( x1 )
S0 '( x1 ) = S1 '( x1 )
S0 ''( x1 ) = S1 ''( x1 )
S1
S0
Sn−2 (xn−1) = Sn−1(xn−1)
Sn−2 '(xn−1) = Sn−1 '(xn−1)
Sn−2 ''(xn−1) = Sn−1 ''(xn−1)
Sn-1
…
Sn-2
…
x0
x1
x2
…
y = f ( x)
xn-2
xn-1
xn
x
S k ( x ) = ak + bk ( x − xk ) + ck ( x − xk ) 2 + d k ( x − xk )3
GHO
IA - MA-33A
6
Interp. y Aprox. de Funciones:
1) Mot. 2: Mínimos Cuadrados Discretos
z
+
+
+
zk = β 0 + β1 xk + β 2 yk + ε k
++ +
+
+ +
+
+
+
+ +
+ +
+ + + +
+
+
+
+
+
+
+ + +
+
y
+
+
+
+
+
+
+
+ + + + +
+
+
Dados n puntos ( xk , yk , zk )
+
+
+ +
+
+
+
+
+
Encontrar la recta que
+
+
+
+
+
+
mejor los aproxima:
+
+
+
+
+
n
+
2
+
+
z
[
∑
β β
x
min
β0 , 1 ,
GHO
IA - MA-33A
2
k =1
k
− ( β 0 + β1 xk + β 2 yk ) ]
7
Interp. y Aprox. de Funciones:
1) Mot. 2: Mínimos Cuadrados Discretos
ƒ Regresión Lineal Bidimensional:
n
min  T 
2
z
−



x


y

∑ k 0 1k 2k
k1
ƒ Ecuaciones Normales:
n
∑
∑
GHO
n
k1
n
k1
xk
yk
n
n
xk
yk
∑ k1
∑k1
n
n
2
x
∑ k1 k ∑k1 x k y k
n
∑nk1 x k y k ∑k1
y 2k
IA - MA-33A
0
1
2

n
zk
∑k1
n
∑ k1 x k zk
∑ nk1 y k zk
8
Interp. y Aprox. de Funciones:
1) Motivación 3: Aproximación de Taylor
1
Aproximación de Taylor para Campana de Gauss
0.9
f(x) y Taylor
0.8
f ( x) = exp(− x 2 )
0.7
x4
pT (x) = 1− x +
2
0.6
2
0.5
0.4
-1
GHO
Campana Gauss
Taylor 4 Orden
-0.5
0
x
IA - MA-33A
0.5
1
9
Interp. y Aprox. de Funciones:
1) Motivación 3: Aproximación de Taylor
2
Aproximación de Taylor de f(x)=ln(x +1)
1.2
1
f ( x) = ln( x 2 + 1)
Función y Taylor
0.8
x4
pT (x) = x −
2
2
0.6
0.4
0.2
0
Función
Taylor
-0.2
-0.4
-1.5
GHO
-1
-0.5
0
x
IA - MA-33A
0.5
1
1.5
10
Interp. y Aprox. de Funciones:
1) Mot. 4: Mínimos Cuadrados Contínuos
ƒ Sea f ∈ ζ [a, b]. Se quiere determinar un
polinomio pn ( x) de grado n según MCC:
b
bi + j +1 − a i + j +1
δ ij =
i + j +1
min ε T = ∫ [ f ( x) − pn ( x) ] dx
pn ( x )
2
a
tes
n
Matriz tipo Hilbert !
c ie
i
f
e
co
ƒ Ecuaciones Normales:
b
b
 a x 0 dx  a x 1 dx
b
b
 a x dx  a x dx
1

b
GHO
2
b

b 3
x dx
a

b
b
 a x 2 dx   a x n dx

b
b
 a x

n1
dx

b
 a x dx  a x dx  a x dx IA - MA-33A
 a x dx
n
n1
n2
2n
b
 a x 0 fxdx
a0
a1

an
b

 a x 1 fxdx

b
 a x n fxdx 11
Interp. y Aprox. de Funciones:
1) Mot. 4: Mínimos Cuadrados Contínuos
ƒ Sea f ( x) = sin(π x) . Determinemos p3 ( x)
polinomio de grado 3 según MC:
a0
1/2 1/3 1/4 1/5
a1
1/3 1/4 1/5 1/6
a2
1/4 1/5 1/6 1/7
a3
2
2/
sin(pi*x) v/s -1/20+103/25x-103/25x
1

1/
0.8
3
2 − 4/
sin(pi*x) v/s p 3(x)
1 1/2 1/3 1/4
3
0.6
2 − 6/
p3 ( x) = −4.12x + 4.12x − 0.05
2
0.4
0.2
0
GHO
0
IA - MA-33A
0.1
0.2
0.3
0.4
0.5
x
0.6
0.7
0.8
0.9 12 1
Interp. y Aprox. de Funciones:
2) Interpolación de Lagrange
ƒ Teorema: Si x0 ,x1,…,xn son (n+1) puntos
distintos y si f es una función que se evalúa
en esos puntos ⇒ ∃! polinomio de grado a lo
más n que interpola f en estos puntos:
pL ( xk ) = f ( xk ) ∀k = 0,1,..., n
n
ƒ Donde: pL ( x) = ∑ f ( xk ) Ln,k ( x)
k =0
GHO
IA - MA-33A
13
Interp. y Aprox. de Funciones:
2) Interpolación de Lagrange
ƒ Y a su vez:
(x − x0 )(x − x1)...(x − xk−1)(x − xk+1)...(x − xn )
Ln,k (x) =
(xk − x0 )(xk − x1)...(xk − xk−1)(xk − xk+1)...(xk − xn )
ƒ Es fácil ver que:
⎧ 1 si j = k
Ln ,k ( x j ) = ⎨
⎩ 0 si j ≠ k
ƒ Error de interpolación Lagrange:
GHO
IA - MA-33A
14
Interp. y Aprox. de Funciones:
2) Interpolación de Lagrange
ƒ Teorema: Sean x0,x1…,xn reales distintos
en el intervalo [a,b] y f ∈ζ n+1[a, b]
Entonces: ∀x ∈ [ a, b ] ∃ξ ( x) ∈ ( a, b ) tal que
f ( x) = pL ( x) + RL ( x)
Error Polinomio
Lagrange
GHO
RL (x) =
f
(ξ (x))
(x − x0 )(x − x1)...(x − xn )
(n +1)!
( n+1)
IA - MA-33A
15
Interp. y Aprox. de Funciones:
2) Interpolación de Lagrange: Ejercs.
ƒ Determinar el polinomio de Lagrange de
las siguientes funciones:
f ( x) = cos( x), x sin( x), xe , ln( x + 1), (1 + x)
en los puntos x = 0, 1, 2, 3, 4.
Utilice este polinomio para evaluar:
x
2
1/ 3
f ( x) = −0.5,0.5,1.5, 2.5,3.5, 4.5
Obtenga una cota del error en [0,5].
Determine error absoluto y relativo.
GHO
IA - MA-33A
16
Interp. y Aprox. de Funciones:
2) Interpolación de Lagrange: Ejercs.
ƒ Para la función de error estadístico erf:
erf ( x) =
2
∫
π
x
0
−t 2
e dt
1) Determine el pol. de Taylor de orden 4.
2) Determine el pol. de Lagrange en x=0.2, 0.4,
0.6, 0.8, 1.0, utilizando 1).
3) Determine cotas del error de estas
aproximaciones.
GHO
IA - MA-33A
17
Interp. y Aprox. de Funciones:
2) Interpolación de Hermite
ƒ El polinomio osculante satisface:
Dados:
x0 ,x1 ,…,xn (n+1) reales distintos en [a,b]
m0 ,m1 ,…,mn (enteros no negativos)
Si f ∈ ζ
m
[ a, b] ( m = max m )
0 ≤i ≤ n
i
p(x) es el polinomio de menor grado tal que:
k
k
d p
d f
x = k ( xi ) ∀k = 0,..., mi ∀i = 0,..., n
k ( i)
dx
dx
GHO
IA - MA-33A
18
Interp. y Aprox. de Funciones:
2) Interpolación de Hermite
ƒ Observación:
1) Si n = 0 el polinomio osculante es el
polinomio de Taylor
2) Si mi = 0 ∀i=0,…,n, el polinomio osculante
es el polinomio de Lagrange.
3) Si mi = 1 ∀i=0,…,n, el polinomio osculante
es el polinomio de Hermite.
GHO
IA - MA-33A
19
Interp. y Aprox. de Funciones:
2) Interpolación de Hermite
ƒ Teorema: Si f ∈ ζ [ a, b ] y x0,x1,…,xn son
m
(n+1) reales distintos en [a,b], el único
polinomio de grado a lo más (2n+1) que
interpola f(x) y f’(x) en los puntos xi es el
polinomio de Hermite H2n+1(x) definido por:
n
n
j =0
j =0
H 2 n+1 ( x ) = ∑ f ( x j ) H n , j ( x) + ∑ f '( x j ) Hˆ n , j ( x)
GHO
IA - MA-33A
20
Interp. y Aprox. de Funciones:
2) Interpolación de Hermite
ƒ Donde:
H nj ( x) = (1 − 2( x − x j ) L 'n , j ( x) ) L2n , j ( x)
2
ˆ
H nj ( x) = ( x − x j ) Ln , j ( x)
Ln,j: j-ésimo pol. de Lagrange de grado n.
ƒ Si: f ∈ ζ 2 n+2 [ a, b ] ⇒ ∀x ∈ [a, b] ∃ξ ( x) ∈ (a, b) :
( x − x0 )2 ( x − x1 )2 ...( x − xn )2 (2n+2)
f ( x) = H2n+1 ( x) +
f
(ξ ( x))
(2n + 2)
GHO
IA - MA-33A
21
Interp. y Aprox. de Funciones:
3) Interpolación por Splines Cúbicos
y
S0 ( x1 ) = S1 ( x1 )
S0 '( x1 ) = S1 '( x1 )
S0 ''( x1 ) = S1 ''( x1 )
S n−2 ( xn−1 ) = S n−1 ( xn−1 )
S n−2 '( xn−1 ) = S n−1 '( xn−1 )
S n−2 ''( xn−1 ) = S n−1 ''( xn−1 )
S1
S0
Sn-1
…
Sn-2
…
x0
x1
x2
…
y = f ( x)
xn-2
xn-1
xn
x
S k ( x) = ak + bk ( x − xk ) + ck ( x − xk ) + d k ( x − xk )
2
GHO
IA - MA-33A
3
22
Interp. y Aprox. de Funciones:
3) Interpolación por Splines Cúbicos
ƒ Dada una función f definida en [a,b] y (n+1)
puntos x0=a, x1, x2, ..., xn=b, el spline cúbico S de
f satisface las siguientes condiciones :
a) S(x) es un polinomio cúbico en el subintervalo
[xj, xj+1] denotado por Sj(x) para j=0,1,…,(n-1)
S 0x  a0  b0x − x 0  c 0 x − x 0 2  d0 x − x 0 3
x ∈ x 0 , x 1
S 1x  a1  b1x − x 1  c 1 x − x 1 2  d1 x − x 1 3
x ∈ x 1 , x 2


S n−1x  an−1  bn−1x − x n−1  c n−1 x − x n−1 2  dn−1 x − x n−1 3 x ∈ x n−1 , x n
GHO
IA - MA-33A
n incógnitas
23
Interp. y Aprox. de Funciones:
3) Interpolación por Splines Cúbicos
b) Sj(xj+1) = Sj+1(xj+1) ∀j=0,1,…,(n-2): Continuidad
c) S(xj) = Sj(xj) = f(xj) ∀j=0,1,…,n: Interpolación
d) S’j(xj+1) = S’j+1(xj+1) ∀j=0,1,…,(n-2): Continuidad
primera derivada
e) S’’j(xj+1)=S’’j+1(xj+1) ∀j=0,1,…,(n-2): Continuidad
segunda derivada
f)
Condición de frontera:
i) S’’(x0)=S’’(xn)=0 (Frontera libre o natural)
GHO
ii) S’(x0)=f’(x0) S’(xn)=f’(xn) (Frontera sujeta)
IA - MA-33A
24
Interp. y Aprox. de Funciones:
3) Interpolación por Splines Cúbicos
ƒ Para construir un spline cúbico de f se tiene
que ∀j = 0,1,…,(n-1):
Sj (x) = aj +bj (x − xj ) +cj (x − xj ) + dj (x − xj )
2
3
ƒ Aplicando la condición c) ∀j = 0,1,…,(n-1):
S j ( x j ) = a j = f ( x j ) ∀j = 0,1,...n
aj+1 = Sj+1(xj+1) = Sj (xj+1) =
= aj + bj (xj+1 − xj ) + cj (xj+1 − xj ) + dj (xj+1 − xj )
2
GHO
IA - MA-33A
3
25
Interp. y Aprox. de Funciones:
3) Interpolación por Splines Cúbicos
ƒ Definimos: h j = x j +1 − x j ∀j = 0,1,..., n − 1
ƒ Luego: a j +1 = a j + b j h j + c j h 2j + d j h3j 1
ƒ Se define bn=S’(xn) y bj=S’(xj) ∀j=0,1,...,n-1
Aplicando la condición d) ∀j=0,1,...,n-1:
b j +1 = b j + 2c j h j + 3d j h
2
j
2
ƒ Se define cn=S’’(xn)/2 y aplicando la cond. e):
GHO
c j +1 = c j + 3d j h j ∀j = 0,1,...n − 1 3
IA - MA-33A
26
Interp. y Aprox. de Funciones:
3) Interpolación por Splines Cúbicos
ƒ Despejando dj de 3 y sustituyendo en 1
y 2 se obtienen las ecuaciones:
2
hj
a j +1 = a j + b j h j + (2c j + c j +1 ) ∀j = 0,1,..., n − 1 4
3
b j +1 = b j + h j (c j + c j +1 ) ∀j = 0,1,..., n − 1
5
ƒ
Despejando bj en 4 : (También bj-1)
hj
1
b j = (a j +1 − a j ) − (2c j + c j +1 ) ∀j = 0,1,..., n − 1 6
3
hj
GHO
IA - MA-33A
27
Interp. y Aprox. de Funciones:
3) Interpolación por Splines Cúbicos
ƒ Se obtiene el siguiente SEL ∀j=1,…,n-1: 7
3
3
hj−1c j−1 + 2(hj−1 + hj )c j + hj c j+1 = (a j+1 − a j ) −
(a j − a j−1)
hj
hj−1
ƒ A estas ecuaciones se debe adicionar las
condiciones de frontera: Libre o Sujeta
ƒ Este sist. de ecs. tiene variables: c0,c1,...,cn
ƒ ¿Tiene solución única 7 ?
GHO
IA - MA-33A
28
Interp. y Aprox. de Funciones:
3) Interpolación Spline Cúbico Libre
ƒ Teo: Si se define f en a = x0<x1<...<xn = b,
entonces f tendrá un único spline cúbico
natural (libre) que cumple con las
condiciones de frontera S’’(x0) = S’’(xn) = 0.
ƒ La forma matricial de 7 es …
ƒ Ejercicio: Determinar el spline cúbico libre
de f(x)=sin(πx) en los puntos: 0, ¼ , ½, ¾, 1
GHO
IA - MA-33A
29
Interp. y Aprox. de Funciones:
3) Interpolación Spline Cúbico Libre
ƒ Forma matricial Spline libre 7 :
1
0
h 0 2h 0  h 1 
0
0

0
h1
0

0
0
h1
2h 1  h 2 
h2

0






0

h n−3
2h n−3  h n−2 
h n−2
0
0

0
h n−2
0


0
GHO
IA - MA-33A
2h n−2  h n−1  h n−1
0
1
30
Interp. y Aprox. de Funciones:
3) Interpolación Spline Cúbico Libre
ƒ Forma matricial Spline libre 7 :
0
3
h1
3
h2
a 2 − a 1 −
3
h0
a 1 − a 0
a 3 − a 2 −
3
h1
a 2 − a 1

3
h n−1
a n − a n−1 −
3
h n−2
a n−1 − a n−2
c0
c1

c n−1
cn
0
Incógnitas
GHO
IA - MA-33A
Vector Lado Derecho
31
Interp. y Aprox. de Funciones:
3) Interp. Spline Cúbico Libre: Ejemplo
ƒ Dados los puntos equiespaciados:
x 0  0, x 1 
1
4
, x2 
y 0  sin0  0, y 1  sin 4  
2
2
1
2
3
4
,x3 
, x4  1
, y 2  sin 2   1, y 3  sin 3

4
2
2
, y 4  sin  0
ƒ Se deben calcular primero:
a 0  0, a 1 
2
2
0
0
0
c0
h1
0
0
c1
h2
0
c2
2h 2  h 3  h 3
c3
h 0  h1  h2  h 3 
1
0
h 0 2h 0  h 1 
0
h1
2h 1  h 2 
0
0
h2
0
0
0
GHO
1
4
0
1
IA - MA-33A
c4
, a 2  1, a 3 
2
2
, a4  0
0

3a 2 −a 1
h1
−
3a 1 −a 0 
h0
3a 3 −a 2
h2
−
3a 2 −a 1 
h1
3a 4 −a 3
h3
−
3a 3 −a 2 
h2
0
32
Interp. y Aprox. de Funciones:
3) Interp. Spline Cúbico Libre: Ejemplo
1
0
0
0
0
c0
0
c0
0
1
4
1
1
4
0
0
c1
−4. 970 6
c1
−3. 672 3
0
1
4
1
1
4
0
c2
0
0
1
4
1
1
4
c3
−4. 970 6
c3
−3. 672 3
0
0
0
0
1
c4
0
c4
0
−7. 029 4

c2

b0
3. 1344
d0
−4. 8963
b1
2. 2164
d1
−2. 0281
0
d2
−2. 2164
d3
b2
b3
GHO



−5. 193 3
2. 0281
4. 8963
b k  a k1 − a k  1 − c k1  2c k  h k ∀k  0, . . . , n − 1
3
hk
0, . . . , n − 1 3
d k  1 c k1 − c k  ∀kIA - 
MA-33A
3h k
6
33
Interp. y Aprox. de Funciones:
3) Interpolación Spline Cúbico Sujeto
ƒ Teo: Si se define f en a = x0<x1<...<xn = b,
entonces f tendrá un único spline cúbico
sujeto que cumple con las condiciones de
frontera S’(x0) = f’(x0) , S’(xn) = f’(xn).
ƒ La forma matricial de 7 es …
ƒ Ejercicio: Determinar el spline cúbico sujeto
de f(x)=cos(πx) en los puntos: 0, ¼ , ½, ¾, 1
GHO
IA - MA-33A
34
Interp. y Aprox. de Funciones:
3) Interpolación Spline Cúbico Sujeto
ƒ Forma matricial Spline sujeto 7 :
2h 0
h0
0
0

0
h0
2h 0  h 1
h1
0

0
0
h1
2h 1  h 2
h2

0






0

h n−3
2h n−3  h n−2
h n−2
0
0

0
h n−2
0


0
GHO
IA - MA-33A
2h n−2  h n−1  h n−1
h n−1
2h n−1
35
Interp. y Aprox. de Funciones:
3) Interpolación Spline Cúbico Sujeto
ƒ Forma matricial Spline Sujeto 7 :
3
h0
3
h1
3
h2
a 1 − a 0 − 3f ′ x0
a 2 − a 1 −
3
h0
a 1 − a 0
a 3 − a 2 −
3
h1
a 2 − a 1

3
h n−1
a n − a n−1 −
3f ′ xn  −
GHO
3
h n−1
3
h n−2
a n−1 − a n−2
c0
c1

cn−1
cn
a n − a n−1
Incógnitas
IA - MA-33A
Vector Lado Derecho
36
Interp. y Aprox. de Funciones:
3) Interpolación Spline Cúbico Sujeto
Sea f ∈ C 4a, b con max |f 4 x|  M. Si S es la spline sujeta determinada en los puntos
a≤x≤b
x 0  a  x 1  x 2    x n−1  x n  b, entonces:
max |fx − Sx| ≤
a≤x≤b
5M
384
max x j1 − x j  4 Cota del Error
SC Sujeta
0≤j≤n−1
Sea g ∈ C 2 a, b cualquier función que satisface las condiciones de interpolación sujetas en:
x 0  a  x 1  x 2    x n−1  x n  b para una función f:
gx k   fx k  ∀k  0, 1, . . . , n
g ′x 0   f ′ x 0 , g ′x n   f ′x n 
Entonces, si S es la spline sujeta determinada en esos mismos puntos:
a
a
b
b
|Sx| 2dx ≤ |gx| 2dx
Mínima Oscilación
SC Sujeta
GHO
IA - MA-33A
37
La spline
sujeta S es la que oscila menos de
todas las funciones "suaves" que interpolan
af
Interp. y Aprox. de Funciones:
4) Interpolación v/s Aproximación:
GHO
IA - MA-33A
38
Interp. y Aprox. de Funciones:
4) Resultado Teórico Básico
ƒ Teorema de Aproximación de Weierstrass: Sea
f : [ a, b ] → \ una función continua:
( ∀ ε > 0 ) ( ∃ p ( x ) ) polinomio tal que:
y
| f ( x) − p( x) |< ε ∀x ∈[ a, b]
y = f ( x) + ε
y = f ( x)
y = f ( x) − ε
y = p( x)
x
GHO
IA - MA-33A
39
Interp. y Aprox. de Funciones:
4) Polinomio Taylor:
ƒ Teorema de Taylor: Suponga que:
f ∈ ^ [ a, b ] , f
n
( n +1)
existe en [a, b], x0 ∈ [a, b]
Para cada x ∈ [a,b] ∃ ξ(x) entre x y x0 tal que:
f ( x) = pn ( x ) + Rn ( x)
( n+1)
f (k ) ( x0 )
(ξ (x))
f
k
(x − x0 ) Rn (x) =
(x − x0 )n+1
pn (x) = ∑
(n +1)!
k!
k =0
n
GHO
IA - MA-33A
40
Interp. y Aprox. de Funciones:
4) Polinomio Taylor: Ejemplo 1
x
x2
x2 x3 x4
x 2 x3
1+ x + + +
1+ x + +
1+ x 1+ x +
2 6 24
2 6
2
ex
1
2
2.5
2.666666
2.7083333
2.718281828
0.5
1.5
1.625
1.645833
1.6484375
1.6487212707
0.3
1.3
1.345
1.3495
1.3498375
1.34985880757
0.1
1.1
1.105
1.10516667
1.10517083
1.10517091807
0.01
1.01
1.01005
1.01005017
1.01005017
1.010050167
0.001
1.001
1.0010005
1.00100050000
1.00100050017
1.00100050016
GHO
IA - MA-33A
41
Interp. y Aprox. de Funciones:
4) Polinomio Taylor: Ejemplo 2
ƒ Determine el polinomio de Taylor de quinto
orden para la función:
f ( x) = ln( x + 1)
2
en torno a x0 = 0
ƒ Utilice estos polinomios que aproximan a f
para calcular:
f (0.5), p5 (0.5) y f (1.0), p5 (1.0)
ƒ Cual es el error relativo ?
GHO
IA - MA-33A
42
Interp. y Aprox. de Funciones:
4) Polinomio Taylor: Ejemplo 2
2
Aproximación de Taylor de f(x)=ln(x +1)
1.2
1
f ( x) = ln( x 2 + 1)
Función y Taylor
0.8
x4
pT (x) = x −
2
2
0.6
0.4
0.2
0
Función
Taylor
-0.2
-0.4
-1.5
GHO
-1
-0.5
0
x
IA - MA-33A
0.5
1
1.5
43
Interp. y Aprox. de Funciones:
4) Polinomio de Taylor: Ejercicios
ƒ Ejemplos Polinomio de Taylor de f en
torno a x0=0:
f ( x ) = sin( x ), cos( x ), sin( x ), x sin( x )
1
x
f ( x) = 2
, 2
x +1 x +1
f ( x ) = ln( x 2 + 1), x ln( x 2 + 1)
2
2
n
1
k ⎛ m + k − 1⎞ k
Si f ( x) =
x
⇒ pn ( x) = ∑ ( −1) ⎜
⎟
m
k
(1 + x)
k =0
⎝
⎠
GHO
IA - MA-33A
44
Interp. y Aprox. de Funciones:
4) Polinomio de Taylor: Ejercicios
2
1.5
Aproximacion de Taylor para f(x)= x*sin(x )
f ( x) = x sin( x 2 )
1
7
x
pT (x) = x3 −
6
f(x), g(x)
0.5
0
-0.5
-1
f(x) = x*sin(x 2)
Taylor f(x)
-1.5
-1.5
GHO
-1
-0.5
0
IA - MA-33A
x
0.5
1
1.5
45
Interp. y Aprox. de Funciones:
4) Polinomio de Taylor:
ƒ El polinomio de Taylor no entrega una buena
aproximación de una función en un intervalo.
ƒ Si se quiere aproximar una función en un
intervalo, se puede utilizar:
1) Interpolación o aproximación polinomial
(Standard, Legendre, Chebyshev, etc)
2) Interpolación Aproximación Trigonométrica
3) Técnicas recientes
GHO
IA - MA-33A
46
Interp. y Aprox. de Funciones:
5) Aproximación Método MC Discreto
ƒ Regresión Cuadrática y Cúbica:
n
min  T 
2  2
y
−



x


x
∑ k 0 1k 2k
k1
n
min  T 
2   x 3  2
y
−



x


x
∑ k 0 1k 2k 3k
k1
ƒ Ecuaciones Normales: Sol. única para xi ≠s
n
∑nk1 x k
∑nk1 x 2k
n
3
GHO ∑
x
k1 k
∑ nk1 x k
∑ nk1 x 2k
∑ nk1 x 3k
∑ nk1 x 4k
∑ nk1 x 2k
∑ nk1 x 3k
∑ nk1 x 4k
∑ nk1 x 5k
∑ nk1 x 3k
∑ nk1 x 4k
∑ nk1 x 5k
MA-33A
x 6k
∑IA -nk1
0
1
2
3

∑ nk1 y k
∑ nk1 x k y k
∑ nk1 x 2k y k
∑ nk1 x 3k y k
47
Interp. y Aprox. de Funciones:
5) Aproximación Método MC Discreto
ƒ Regresión Polinomial: (n < m–1)
min  T 
m
m
i1
i1
∑y i − pnx i 2  ∑
2
n
y i − ∑ a k x ki
k0
ƒ Ecuaciones Normales: Sol. única para xi ≠s
∑mi1 x i
m
xi
∑i1
m
x 2i
∑i1


n
m
x 2i  ∑mi1 x ni
∑i1
m
x 3i  ∑ mi1 x n1
∑i1
i



m
m
n2
2n
∑mi1 x ni ∑mi1 x n1
∑
x

∑
x
i
i
i1
i1 i
GHO
IA - MA-33A
a0
a1

an

∑mi1 y i
∑mi1 x i y i

∑mi1 x ni y i
48
Interp. y Aprox. de Funciones:
5) Aproximación Standard MC Continuo
ƒ Sea f ∈ ζ [a, b] . Se quiere determinar un
polinomio pn ( x) de grado n según MC:
b
Matriz tipo Hilbert !
min ε T = ∫ [ f ( x) − pn ( x) ] dx
pn ( x )
2
a
fic
e
co
ƒ Ecuaciones Normales:
b
b
 a x 0 dx  a x 1 dx
b
b
 a x dx  a x dx
1

b
GHO
2
b
b 3
x dx
a

b

b
b
 a x

n1
dx

b
 a x dx  a x dx  a x dx IA - MA-33A
 a x dx
n
n1
es
t
ie n
i,j=0,…,n
b
 a x 2 dx   a x n dx

bi + j +1 − a i + j +1
δ ij =
i + j +1
n2
2n
b
 a x 0 fxdx
a0
a1

an
!
b

 a x 1 fxdx

b
 a x n fxdx 49
Interp. y Aprox. de Funciones:
5) Aprox. Standard MC Continuo: Ejemplo
ƒ Sea f ( x) = sin(π x) . Determinemos p3 ( x)
polinomio de grado 3 según MC std. en [0,1]:
1 1/2 1/3 1/4
a0
2/
1/2 1/3 1/4 1/5
a1
1/1
1/3 1/4 1/5 1/6
a2
1/4 1/5 1/6 1/7
a3
4/3
2 − 0.8
2 − 0.6
6/3
sin(pi*x) v/s p 3(x)

2
sin(pi*x) v/s -1/20+103/25x-103/25x
p3 ( x) = −4.12x + 4.12x − 0.05
2
0.4
0.2
0
GHO
IA - MA-33A
0
50
0.1
0.2
0.3
0.4
0.5
x
0.6
0.7
0.8
0.9
1
Interp. y Aprox. de Funciones:
5) Aprox. Standard MC Continuo: Ejemplo
2
f
(
x
)
=
x
cos(
x
) . Polinomios de grado
ƒ Sea
p8,10 ( x) 8,10 MC standard en [0,4]:
GHO
IA - MA-33A
51
Interp. y Aprox. de Funciones:
5) Aproximación Método MC Continuo
ƒ El conjunto de funciones {φ 0 , φ1 ,..., φ n } es
linealmente independiente en [a,b] si:
c0φ0 ( x) + c1φ1 ( x) + ... + cnφn ( x) = 0 ∀x ∈ [a, b]
ƒ Implica que: c0 = c1 = ... = cn = 0
ƒ Si φ j es un polinomio de grado j ∀ j=0,…,n
⇒ {φ0 ,φ1 ,...,φn } es un conjunto linealmente
independiente para cualquier intervalo [a,b].
GHO
IA - MA-33A
52
Interp. y Aprox. de Funciones:
5) Aproximación Método MC Continuo
ƒ Una función ω(x) es una función de peso en
[a,b] si ω(x) ≥ 0 para x∈[a,b] y ω(x) ≠ 0 en
cualquier subintervalo de [a,b].
f(x)=1/sqrt(1-x2)
4
ƒ Por ejemplo:
ω ( x) =
3.5
3
1
1− x
2.5
2
2
1.5
1
0.5
0
-1
-0.8
-0.6
-0.4
-0.2
0
x
0.2
0.4
0.6
0.8
1
ƒ Sean {φ0 ,φ1 ,...,φn } (n+1) funciones l.i en [a,b].
GHO
IA - MA-33A
53
Interp. y Aprox. de Funciones:
5) Aproximación Método MC Continuo
ƒ Sea f ∈ ζ [a, b] . Se quiere determinar una
función p ( x) de la forma:
n
p ( x) = ∑ akφk ( x)
k =0
φ0,…, φn
funciones l.i.
ƒ que aproxime f ( x) según el criterio de MC
para el peso ω(x):
b
min ε T = ∫ ω ( x) [ f ( x) − p ( x) ] dx
a0 ,...,an
GHO
IA - MA-33A
2
a
54
Interp. y Aprox. de Funciones:
5) Aproximación Método MC Continuo
b
2
⎡
⎤
min ε T = ∫ ω ( x) ⎢ f ( x) − ∑ akφk ( x) ⎥ dx
a0 ,...,an
k =0
⎣
⎦
a
b
n
b
b
a 20xdx a 01 xdx  a 0n xdx
b
b
b
a 10 xdx a 21xdx  a 1n xdx


b

b

b
a n0 xdx a n1 xdx  a 2nxdx
b
a0
 af0 xdx
a1
 af1 xdx

an
b


b
 afn xdx
ƒ Si las funciones {φ , φ 2 ,..., φ n } son ortogonales
b
2
n
⎡
⎤
min ε T = ∫ ω ( x) ⎢ f ( x) − ∑ akφk ( x) ⎥ dx
k =0
⎣
⎦ 1
a
con respecto a ω(x) en [a,b] se tiene que:
GHO
IA - MA-33A
55
Interp. y Aprox. de Funciones:
5) Aproximación Método MC Continuo
⎧ 0 si j ≠ k
∫a (ωφ jφk )( x)dx = ⎨⎩α j si j = k
b
b
α j = ∫ (ωφ j 2 )( x)dx > 0
a
ƒ En este caso, las ecuaciones normales
quedan diagonales:
b
a 20xdx
0
GHO
a0
0
a1


 af1 xdx
0
a 21xdx 
b
b
 af0 xdx

0



0
0
  2n xdx
b
a
IA - MA-33A
an
b


b
 afn xdx
56
Interp. y Aprox. de Funciones:
5) Aproximación Método MC Continuo
ƒ Teo: El conjunto de polinomios {φ 0 , φ1 ,..., φ n }
definidos recursivamente es ortogonal en [a,b]
con respecto a la función de peso ω(x): (cualquiera)
φ0 ( x) = 1 φ1 ( x) = x − B1
φk ( x) = ( x − Bk )φk −1 ( x) − Ckφk −2 ( x) ∀k ≥ 2
xω ( x) [φ
∫
=
∫ ω ( x) [φ
2
b
Bk
GHO
k −1
a
b
a
k −1
( x) ] dx
2
( x) ] dx
Ck
IA - MA-33A
∫
=
b
a
xω ( x)φk −2 ( x)φk −1 ( x)dx
∫ ω ( x) [φ
2
b
a
k −2
( x) ] dx
57
Interp. y Aprox. de Funciones:
5) Aproximación Polinomios de Legendre
ƒ Teo: El conjunto de polinomios {φ 0 , φ1 ,..., φ n }
de Legendre definidos recursivamente es
ortogonal en [-1,1] c/r a la f. de peso ω(x)=1:
φ0 (x) = 1 φ1(x) = x − B1
φk (x) = (x − Bk )φk−1(x) − Ckφk−2 (x) ∀k ≥ 2
x [φ
∫
=
∫ [φ
2
1
Bk
GHO
−1
k −1
1
−1
k −1
( x) ] dx
2
( x) ] dx
Ck
∫
=
IA - MA-33A
1
−1
xφk −2 ( x)φk −1 ( x)dx
∫ [φ
2
1
−1
k −2
( x) ] dx
58
Interp. y Aprox. de Funciones:
5) Aproximación Polinomios de Legendre
ƒ Polinomios de Legendre {φ0 ,φ1 ,φ2 ,φ3 ,φ4 }
φ0 (x) = 1
φ1(x) = x
φ2 (x) = x2 − 13
3
φ3 (x) = x − 53 x
4
6 2
φ4 (x) = x − 7 x + 353
dk
φk ( x) = k ⎡⎣( x 2 − 1) k ⎤⎦
dx
GHO
Fórmula
IADe
- MA-33A
Rodrigues
59
Interp. y Aprox. de Funciones:
5) Aproximación Polinomios de Legendre
ƒ Teo: El conjunto de polinomios {φ0 ,φ1 ,...,φn }
de Legendre definidos recursivamente es
ortogonal en [-1,1] c/r a la f. de peso ω(x)=1:
ψ 0 (x) = 1 ψ1(x) = x
Gram
Schmidt
ψ 2 (x) = (3x −1) ψ3 (x) = (5x − 3x)
1
2
2
1
2
3
ψ k+1(x) = ( 2kk++11 ) xψ k (x) − ( kk+1 )ψ k−1(x) ∀k ≥ 2
k
GHO
1 d
k
2
⎡
( x − 1) ⎤⎦
ψ k ( x) = k
k ⎣
2 k ! dx
IA - MA-33A
Fórmula
De Rodrigues
60
Interp. y Aprox. de Funciones:
5) Aproximación Polinomios de Chebyshev
ƒ Teo: El conjunto de polinomios {T0 , T1 ,..., Tn }
de Chebyshev definidos recursivamente es
2 −1/2
ortogonal en [-1,1] c/r a la f.p. ω(x) = (1− x ) :
T0 (x) = 1 T1(x) = x
Tk+1 (x) = 2xTk ( x) − Tk−1 (x) ∀k ≥ 1
ƒ Se utilizan para ubicar los puntos interpolantes
debido a que minimizan el error de
interpolación de Lagrange
GHO
IA - MA-33A
61
Interp. y Aprox. de Funciones:
5) Aproximación Polinomios de Chebyshev
Polinomios de Chebyshev
Polinomios de
1
Chebyshev
T0
T3
T4
T0,T1,T2,T3,T4
0.5
T1
0
-0.5
T2
-1
GHO
-1
-0.8
-0.6
IA - -0.4
MA-33A
-0.2
0
x
0.2
0.4
0.6
0.8
162
Interp. y Aprox. de Funciones:
5) Aproximación Polinomios de Chebyshev
ƒ Teo: El polinomio de Chebyshev Tn ( x) de
grado n≥1 tiene n ceros simples en [-1,1]
definidos por:
⎛ 2k −1 ⎞
xk = cos ⎜
π ⎟ k = 1,2,..., n
⎝ 2n ⎠
ƒ Adicionalmente Tn ( x) alcanza sus extremos
en:
GHO
⎛ kπ ⎞
k
ˆ
xˆk = cos ⎜
T
x
k = 0,1, 2,..., n
=
−
(
)
(
1)
⎟ n k
⎝ n ⎠
IA - MA-33A
63
Interp. y Aprox. de Funciones:
5) Aproximación Polinomios de Chebyshev
ƒ Teo: Si pL ,C ( x) es el polinomio de Lagrange de
grado n definido en los ceros del polinomio de
Chebyshev Tn ( x) , se tiene que:
1
( n +1)
max f ( x) − pL ,C ( x) ≤ n
max f
( x)
x∈[ −1,1]
2 (n + 1)! x∈[ −1,1]
n +1
f
∈
ζ
[−1,1]
Para cualquier
GHO
IA - MA-33A
64
Interp. y Aprox. de Funciones:
5) Aproximación Polinomios de Chebyshev
x
ƒ Ejemplo: Interpolación de f ( x) = xe en [0,1.5]
pL ( x )
f (x) − pL(x) pL,C (x)
f (x) − pCL(x)
x
f ( x) = xe
0.15
0.1743
0.1969
0.0226
0.1868
0.0125
0.35
0.4967
0.5121
0.0154
0.5064
0.0097
0.75
1.588
1.572
0.016
1.571
0.017
1.15
3.632
3.650
0.018
3.644
0.012
1.35
5.208
5.237
0.029
5.224
0.016
GHO
x
IA - MA-33A
65
Interp. y Aprox. de Funciones:
6) Interpolación Trigonométrica
ƒ Teorema de Interpolación Trigonométrica:
Considere 2m puntos ( x j , y j ) j=0,1,…,2m-1,
con: xj = −π + jπ / m (dist. uniforme en [-π,π]).
Dados los coeficientes:
ak ∀k = 0,..., n
bk ∀k = 1,..., n − 1
Se define la función de interpolación
n−1
Sn ( x j ) = a0 + an cos(nx j ) + ∑( ak cos(kx j ) + bk sin(kx j ) )
k =1
GHO
IA - MA-33A
66
Interp. y Aprox. de Funciones:
6) Interpolación Trigonométrica
ƒLos coeficientes ak , bk que minimizan el error
de interpolación trigonométrico :
min ε T =
ak ,bk
2 m−1
∑ ⎡⎣ y
j =0
j
− Sn ( x j ) ⎤⎦
2
ƒ Están dados por:
2 m−1
ak = ∑ y j cos(kx j ) ∀k = 0,1,2,..., n
j =0
2 m−1
GHO
bk = ∑ y j sin(kx j ) ∀k = 1,2,..., n − 1
j =0
IA - MA-33A
67
Interp. y Aprox. de Funciones:
6) Aproximación Trigonométrica
ƒ Teo: Las funciones Fn = {φ0 ,φ1 ,...,φ2 n−1} son ortonales en [-π,π] para la función de peso ω(x) = 1:
1
φ0 ( x) =
2
φk ( x) = cos(kx) k = 1, 2,..., n
φn+k ( x) = sin(kx) k = 1,..., n − 1
ƒ El conjunto de funciones generado por Fn se
denomina polinomios trigonométricos Π n
GHO
IA - MA-33A
68
Interp. y Aprox. de Funciones:
6) Aproximación Trigonométrica
ƒ Para una función f ∈ ζ [−π , π ] la aproximación
de mínimos cuadrados en
Π n es de la forma:
n −1
a0
S n ( x) = + an cos(nx) + ∑ ( ak cos(kx) + bk sin(kx) )
2
k =1
ƒ donde los coeficientes ak , bk están dados por:
ak =
GHO
1
π
π
∫π f ( x)cos(kx)dx
bk =
−
k=0,1,…,n
IA - MA-33A
1
π
π
∫π f ( x)sin(kx)dx
−
k=1,2,…,n-1
69
Interp. y Aprox. de Funciones:
6) Aproximación Trigonométrica
Aproximación
trigonométrica
de:
f(x)=abs(x) y S(x)=1/2π - 4cos(x)/π - 4/9cos(3x)/π
3
2.5
f ( x) = x
x ∈ [−π , π ]
π
4
f(x) y S(x)
2
1.5
1
4
S3 ( x) = − cos( x) − cos(3x)
2 π
9π
0.5
0
GHO
-3
-2
IA - MA-33A
-1
T3
0
x
1
2
3
70
Interp. y Aprox. de Funciones:
6) Aprox. – Interp. Trigonométrica
ƒ Ejercicios
1) Determine los polinomios trigonométricos
continuos de S2(x) y S3(x) de x2
2) Determine el polinomio trigonométrico
continuo Sn(x) de ex
3) Determine el pol. trigonométrico discreto
S3(x) de f(x) = excos(x) para m = 4 en [-π,π]
4) Determine el pol. trigonométrico discreto
S4(x) de f(x)= x2sin(x) para m = 5 en [0,1]
GHO
IA - MA-33A
71
Interp. y Aprox. de Funciones:
Bibliografía
1) R. Burden & J. D. Faires, Análisis
Numérico, Séptima Edición, Thomson
Learning, 2002.
2) J. Stoer & R. Burlisch, Introduction to
Numerical Analysis, Second Edition,
Springer, 1992.
3) G. Hernández: Apuntes de Cálculo
Numérico 2007
GHO
IA - MA-33A
72