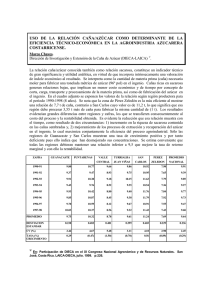
aproximacion a un canje de “suertes” de caña de azucar a

XV INTERNATIONAL CONFERENCE ON INDUSTRIAL
ENGINEERING AND OPERATIONS MANAGEMENT
The Industrial Engineering and the Sustainable Development: Integrating Technology and Management.
Salvador, BA, Brazil, 06 to 09 October - 2009
APROXIMACION A UN CANJE DE
“SUERTES” DE CAÑA DE AZUCAR A
TRAVES DE UN MODELO DE
PROGRAMACIÓN LINEAL
Mariela Galindo Barbosa (Univalle)
mariegaba@gmail.com
El siguiente articulo presenta una propuesta de modelo matemático de
programación lineal entera, como herramienta para que los ingenios, y
en particular estos dos ingenios, que permite hacer una asignación de
suertes ya sean propias o del ootro ingenio, de tal forma que minimice
sus costos anuales de cosecha. Este modelo contempla los otros costos
del proceso de cosecha que hasta ahora no son tomados en cuenta en
este tipo de decisiones empíricas. Lo que permitiría a los ingenios
conocer con anterioridad cuales suertes podrían canjear y tener
mejores criterios para la negociación de dicho canje.
Palavras-chaves: Canje, Suertes, Caña de Azucar, Programación
lineal entera
1.1
1. INTRODUCCION
Los ingenios de Colombia se encuentran ubicados, en su totalidad en la zona plana
interandina conocida como Valle geográfico del río Cauca, el cual se extiende desde el
municipio de Santander de Quilichao (Cauca) en el sur, cruza el departamento del Valle del
Cauca y finaliza en el norte en los municipios de La Virginia (Risaralda) y Belálcazar
(Caldas) [1]. En esta región se ha desarrollado un cluster azucarero conformado por más de
1.500 agricultores que cultivan algo más de 205.000 hectáreas, catorce ingenios, más de
cuarenta empresas de alimentos y bebidas, once productores de alcohol y licores, dos
cogeneradores de energía, un productor de papel, una industria sucroquímica y multitud de
empresas proveedoras de los bienes y servicios que la cadena productiva demanda [2]. La
cercanía de estas industrias y la importancia de la caña de azúcar como una de las principales
agroindustrias de Colombia, pues participa con casi el 50% de las exportaciones totales del
país, ha permitido a la Industria Azucarera por ser uno de los sectores mas organizados a
nivel gremial.
Lo anterior le ha permitido ser uno de los sectores más destacados en el uso de tecnología de
vanguardia en los procesos productivos tanto en el campo como en la fábrica, manteniendo
así excelentes estándares de eficiencia y calidad en las empresas que lo conforman como en
sus productos. A pesar de esto, el sector se ve amenazado por la globalización de los
mercados, como se observa en la disminución de las exportaciones, presentándose una
reducción del 6% en ellas en el periodo 2006 – 2007 [3], lo que lo lleva a enfrentar grandes
retos tendientes a la búsqueda de estrategias que le permitan seguir siendo competitivo. Por
esta razón los ingenios, encargados de los primeros dos eslabones de la cadena de suministro:
producción (cultivo, corte y transporte) y procesamiento de la caña de azúcar, buscan
disminuir especialmente los costos relacionados con la producción de caña de azúcar.
Precisamente buscando reducir los costos de producción, dos ingenios de esta región
determinaron, desde hace ya algunos años de manera empírica, que en esta situación
particular que afecta a cada ingenio, se debe plantear la posibilidad de realizar un canje de
suertes (mínima extensión de tierra, en la que se dividen las haciendas cultivadas de caña, por
cada ingenio), que manejan los ingenios; con el objetivo de disminuir los costos de transporte
asociados a la cosecha (periodo en el cual la suerte esta lista para ser cortada y llevada a los
patios del ingenio) de la suerte; logrando el objetivo esperado.
Este articulo artículo muestra una propuesta de una herramienta de decisión, mediante un
modelo matemático de programación lineal entera, al canje de suertes que puede tener dos
opciones: una en términos de azúcar (kilo de azúcar) a nivel de industria y otra, que será la
abordada en este articulo, en términos de tonelada de caña a nivel de la cosecha; que le
permitirá a los ingenios interesados considerar algunos otros factores relevantes como: costos
de mano de obra, cantidad de sacarosa o rendimiento de la caña de azúcar, etc., además de los
costos de transporte, dando una mirada mas aproximada a la realidad de los costos de cosecha
que se asocian a las suertes canjeables.
1.1 Revisión de Literatura
En la revisión de literatura, se comprobó que en el sector azucarero colombiano existen
investigaciones importantes relacionadas con la optimización de los costos de transporte al
interior de los ingenios, haciendo un análisis de los sistemas de corte, alce y transporte. No
obstante; no se ha realizado una implementación real y seguimiento sistemático que
permitan validar sus resultados en la práctica como consecuencia de la realización de
aplicaciones sucesivas. Tampoco se identificó ningún estudio que involucrara la integración
2
de los ingenios para llevar a cabo un objetivo común que permitiera el beneficio del sector
azucarero, por lo que se evidencia que aún falta mucho por explorar en el sector
agroindustrial.
A continuación se presentan dos estudios colombianos encontrados, que haciendo uso de la
investigación de Operaciones, han tratado de acercarse al problema planteado de Costos de
Transporte de Caña de azúcar:
• Díaz (2000), en su estudio, presenta la formulación y desarrollo de un modelo
matemático para la secuenciación óptima de la cosecha de la caña de azúcar, que
considera el tiempo más temprano y el tiempo más tarde de cosecha (ventana de
tiempo). El problema desarrollado consistió en encontrar una ruta óptima, donde la
alzadora debía visitar cada suerte exactamente una vez partiendo de una suerte fija, el
tiempo de desplazamiento fuera mínimo y cumpliera con las restricciones de la
ventana de tiempo.
Finalmente, el resultado que se obtuvo fue un algoritmo para el recorrido óptimo de
las alzadoras. Después de validar el modelo con datos reales, los resultados fueron
comparados con la ruta que siguieron las alzadoras en el mes de prueba, demostrando
la ventaja del algoritmo ya que se disminuyó significativamente el tiempo de
desplazamiento [4].
• Viveros (1996), presenta la formulación de un modelo de asignación para optimizar el
proceso de la cosecha de la caña de azúcar, el cual consideró los siguientes costos:
- De corte, alce y transporte.
- Adecuación y preparación del suelo y la siembra.
- De fumigación con madurante y sus beneficios sobre el rendimiento y materia
extraña.
- De desplazamiento de un área a otra.
- Los que ocurren desde que un área es factible de ser cosechada hasta que se inicia
su cosecha y los provocados por la materia no útil para el procesamiento de la
caña.
En el trabajo también se describe y analiza como obtener la información de entrada al
modelo de asignación a partir de datos accesibles recogidos del proceso de cultivo,
cosecha y los diferentes modos de transporte de caña [5].
A nivel internacional esta misma inquietud, ha sido abordada por algunos países productores
de Caña de Azúcar como Cuba, Australia y otros, quienes han visto en la aplicación de
Investigación de Operaciones una manera de disminuir dichos costos y lograr ser más
competitivos en el mercado del azúcar.
En Cuba, dada la necesidad del funcionamiento sincronizado del sistema de recolección de la
caña de azúcar y de reducir al mínimo posible las fallas de sus eslabones: corte, alce,
transporte y recepción, se han realizado un gran número de investigaciones tendientes a
disminuir los costos de transporte, mediante la tarea de establecer la relación más eficiente y
funcional de los proveedores de caña desde los diferentes bloques cañeros a los centros
receptores, dentro y entre centrales azucareros, con el objetivo de disminuir los costos totales
de transporte y de lograr una mayor racionalidad de los medios utilizados en la recolección de
la cosecha.
De esta manera, en el trabajo realizado por López, et.al. (2005), se presenta una propuesta de
solución al problema de la minimización del costo del transporte de la caña de azúcar,
cosechada en diferentes campos cañeros y transportada hasta un central azucarero (Ingenio)
para su procesamiento, mediante un modelo de programación lineal entero mixto.
3
La complejidad del problema viene determinada por el número de variables y restricciones a
tener en consideración. En las restricciones se hace referencia a la necesidad de
abastecimiento continuo del central, los medios utilizados en la cosecha, los distintos tipos de
transporte y las rutas de aprovisionamiento, caracterizadas por la existencia de centros de
acopio de la caña, para el posterior transporte de la caña al central por ferrocarril.
El modelo presentado en el documento es capaz de resolver el problema de transportar caña
de azúcar desde los campos al molino al mínimo costo en un día de trabajo, determina las
rutas y las capacidades para transportar la caña y así asegurar el abastecimiento continuo del
molino. Los resultados demuestran que el modelo no es solamente útil para minimizar el costo
de transporte, sino también para la programación diaria de caña [6].
De acuerdo con Marrero, et.al. (2001), las técnicas y modelos de la Investigación de
Operaciones permiten apoyar decisivamente la toma de decisiones logísticas en la cadena de
corte, alce y transporte de la caña de azúcar. Por tanto, en el estudio se ha considerado un
modelo económico matemático de programación multicriterio para proponer la solución
óptima para el transporte de la caña hasta la báscula del central (Ingenio), teniendo en cuenta
que el principal problema que afecta el transporte de la caña es el incumplimiento de los
plazos establecidos para la entrega de la caña a su cliente inmediato, en la cadena de
transporte; además, se debe tener en consideración que se trata de una decisión que requiere
evaluar varios criterios de desempeño y no un solo objetivo. Por lo que en este estudio se
utilizó la programación multimeta que permite evaluar el transporte de la caña de azúcar
valorando varios criterios de desempeño [7].
Infante (2001), presenta un trabajo que ofrece aspectos esenciales de una metodología para
obtener las vinculaciones óptimas desde los bloques cañeros a los centros receptores de caña,
mediante la utilización de métodos y modelos económico-matemáticos; los modelos
planteados permiten realizar un análisis integral del corte, alce, transporte, recepción y
producción de azúcar. Para dar solución a la problemática planteada en el trabajo se analizan
y desarrollan modelos de Programación Matemática como los modelos de Programación
Lineal relacionados con las vinculaciones cañeras dentro y entre centrales azucareros [8].
Los resultados prácticos más relevantes aportados por la aplicación de esta metodología
desde el punto de vista económico, técnico y productivo es que se logra una disminución en el
costo total de transporte anual en un rango del 9% al 15% [9].
Por otra parte, en Grecia, un estudio que busca reducir precisamente los costos de transporte
asociados a la cadena de abastecimiento lo presenta Ioannou (2005), quien evidencia las
ineficiencias operacionales y del servicio al cliente. En este proyecto se hace un estudio de la
cadena de abastecimiento en la industria de azúcar Helénica analizando los costos logísticos,
la demanda de los clientes y el desarrollo de un modelo de transporte apropiado que se derive
en la distribución óptima de sus productos. En el modelo se incorporan el nivel de producción
de las diversas plantas de fabricación, las capacidades de almacenaje, la producción y
distribución de plantas y el transporte. Los resultados generados por el modelo matemático
logran ahorros en sus costos de transporte anuales de US$3.5 millones constituyendo casi el
40% de los gastos operados en el campo, asociado a una mejora en el servicio al cliente pues
se mejoró la cobertura de la demanda [10].
Por último, en Australia se encuentran numerosas investigaciones y modelos de Investigación
de Operaciones aplicados a la Industria Azucarera, que arrojan significativa ganancia en su
competitividad a nivel internacional en la producción de azúcar de caña. Cabe anotar que a
diferencia de Colombia y Cuba, los sistemas de transporte de la caña de azúcar a los ingenios
solo dependen de la integración entre los sistemas de cosecha y transporte; gracias a la
tecnología usada en ellos.
4
A continuación se encuentran algunos de los trabajos encontrados, que guardan mayor
relación con el tema tratado en esta propuesta.
Higgins, et al. (1998), presentan un aplicación de un modelo de optimización para la
producción de caña de azúcar, teniendo en cuenta factores, propios de la agricultura como,
fecha y edad de cosecha, con el fin de aprovechar al máximo el cultivo de la caña en las
diferentes fincas (suertes) de acuerdo a características como ubicación de la zona geográfica,
variedad de caña a sembrar, entre otras propias de la regiones Australianas. El resultado de
este estudio mostró un aumento del 16% en el beneficio neto cuando todas las cosechas
fueron sembradas inmediatamente después del arado [11].
En un estudio sobre el perfeccionamiento de la cosecha en Australia que permite mejorar la
producción, Higgins (2002), presenta la problemática de permanecer competitivos
internacionalmente mediante el mejoramiento en infraestructuras más eficientes a través de
modelos de optimización [12]. En el momento de publicación de este artículo el modelo solo
se hallaba en la etapa de aplicación y no se describen resultados obtenidos aún.
Es así como el mismo Higgins y Muchow (2003) plantean la utilización de un modelo de
asignación de suertes a sembrar, para optimizar la producción de azúcar; el cual logra tener en
cuenta la variabilidad de factores como el clima, ubicación geográfica, tipo de caña y otros
que inciden notablemente en tiempo de cosecha de la caña. Este modelo fue aplicado a varios
ingenios de las diferentes regiones australianas logrando unos aumentos de utilidades hasta de
AU $157/ha [13].
El anterior estudio presenta algunas similitudes con el modelo propuesto en el artículo como:
•
Uso de una variable de asignación entera binaria, definida de la siguiente manera, para
la planeación de la cosecha en un horizonte de un año [14].
1 si la suerte i
es cosechada en el
periodo j durante una estación de
X ij =
cosecha.
0 de lo contrario.
•
La participación de diferentes dueños de suerte que abastecen a diferentes ingenios
con capacidades de producción diferentes en una determinada región. Observándose
así como el pensar como una cadena productiva y la aplicación de técnicas apropiadas
puede lograr mayores beneficios para cada uno de los participantes en ellas.
Higgins, et. al. (2004), presenta la problemática de la industria azucarera Australiana, donde
se refleja la falta de integración de la cadena de valor ante las ineficiencias entre el sistema de
cosecha y el sistema de transporte; dado el excesivo número de máquinas cosechadoras
concentradas en una misma región y que son propiedad de los ingenios, los contratistas y los
cultivadores.
Este problema se aborda a través del desarrollo de una estructura que permite integrar estos
dos sistemas, mediante la reducción en el número de cosechadoras en la región y la
implementación de mejoras en la práctica de la cosecha, con el objetivo de reducir los costos
de producción. El desarrollo e implementación lo describe Higgins analizando dos casos al
interior de las áreas de los molinos de la industria azucarera en Australia. El modelo fue
aplicado en una región perteneciente a un ingenio, en el 2003, logrando un incremento en sus
utilidades de AU$1.000.000 por año [15].
5
En esta línea, Higgins y Davies (2005) proponen y aplican un modelo de simulación
estocástica para la planeación de la capacidad del transporte de la caña de azúcar hasta los
molinos, haciendo uso de un medio de transporte como el tren. Con él lograron estimar el
número óptimo de máquinas requeridas y numero óptimo de vagones usados; minimizar los
retrasos por imprevistos y optimizar las horas de salida de las maquinas cortadoras. El
modelo también fue aplicado con éxito en una región dedicada a la producción de azúcar
Australiana, reduciendo costos en transporte y cosecha de la caña de azúcar [16].
En otra investigación, de nuevo Higgins (2006), explica como la presión que implica
permanecer competitivo en los mercados internacionales ha forzado a los molinos de azúcar
Australianos a reducir los costos operacionales, a través de la optimización de las rutas de los
vehículos de transporte que permiten tener la oportunidad de mantener un flujo constante y
reducir los tiempos en que los automotores están en espera de iniciar los recorridos, no es una
actividad fácil dado que se debe atender un gran número de cosechas con ubicaciones
diferentes.
Para el desarrollo de la investigación se implementó un modelo de programación entera mixta
que presenta las rutas de operaciones del transporte, se aplicaron dos meta-heurísticos para
encontrar la solución del modelo. El resultado obtenido en la aplicación del modelo de
integración de la cosecha y el sistema de transporte fue un ahorro potencial en sus costos de
AU$240.000 al año [17].
Hasta el momento, el último trabajo similar que hace uso de modelos de optimización para
ser aplicados a un caso estudio, es el realizado por M. Grunow y otros (2007), en un ingenio
en Maracaibo Venezuela. Aquí, haciendo uso de un modelo de planeación jerárquico a tres
niveles que van desde la planeación del cultivo de caña hasta la cosecha (corte, alce y
recolección) de ella, y manteniendo constante del suministro de caña de azúcar al ingenio,
logra minimizar los costos asociados a estas actividades, entre ellos obviamente el costo de
transporte [18].
Como se puede observar en lo expuesto a lo largo de este aparte, la minimización de costos se
ha planteado pero ninguno enfocado a la integración de varios actores de la cadena de
suministro a través de un “modelo de optimización de canje de caña” buscando así un
enfoque gana a gana para todos los que en ella intervienen, a través de una herramienta como
las planteadas anteriormente. Por esto, el modelo propuesto en este articulo, es hasta el
momento único en su género, dando así una razón mas para justificar su relevancia, la cual se
espera sea para beneficio de al menos un sector de los cultivadores de caña de azúcar y
productores de azúcar, como sea logrado en otros países al aplicar estas herramientas de
optimización.
2. CASO BASE
Como se mencionó anteriormente la propuesta del modelo de decisión, se basará en la
información suministrada por dos ingenios reales ubicados en el Valle geográfico del Río
Cauca dedicados al cultivo de la caña de azúcar y producción de azúcar a partir de ella
(además de otros productos), quienes ya practican de forma empírica el canje de suertes de
caña para su cosecha.
A continuación se presente unas generalidades del cultivo de caña de azúcar, en Colombia, y
las características relevantes del proceso de cosecha (corte, alce y transporte) de la caña de
azúcar, que permitan ubicar con más precisión las especificidades del modelo.
6
2.1 Cultivo de Caña de Azúcar
La región del Valle del Río Cauca es una región que posee las condiciones idóneas para el
crecimiento de la caña de azúcar: brillo solar permanente e intenso a lo largo del año, caída
adecuada de temperatura entre el día y la noche, disponibilidad de agua, lluvias adecuadas y
fertilidad en los suelos. El cultivo de la caña de azúcar se hace en forma continua durante todo
el año, su ciclo de maduración es de aproximadamente 12 meses y por lo tanto todo el año se
puede cosechar caña y no en forma estacional o por zafra (periodo en el año durante el cual se
puede cosechar la caña pues el bastón de la caña de azúcar es mas alto y de contenido de fibra
aceptable) como ocurre en el resto del mundo.
Los dos ingenios de este caso, al igual que todos los ingenios de Colombia, pueden
mantenerse cultivando y cosechando caña de azúcar en cualquier mes del año, lo que hace que
se pueda mantener una producción constante de azúcar (o cualquier otro producto que use a la
caña de azúcar como materia prima) y no por periodos, como ocurre en países como
Venezuela [19].
2.2 Proceso de Cosecha (corte, alce y transporte)
En este aparte se describirá el proceso de cosecha y los costos asociados a él, pues será el
proceso base para la propuesta del modelo matemático del canje de caña planteado en este
articulo. La cosecha de la caña de azúcar tiene lugar en el momento en que la planta se
encuentra en su etapa de maduración y consiste en tres actividades básicas, llamadas
subprocesos en este caso, que permiten su realización: Corte, alce y transporte; tiene como
objetivo principal el abastecimiento diario de caña al ingenio.
Por lo tanto este proceso, para los dos ingenios, está enmarcado dentro de las necesidades de
la planta que de acuerdo a las condiciones del mercado y a su capacidad, presupuesta una
producción en un horizonte de planeación de un año; bajo estos requerimientos el
departamento de Campo de los ingenios, hacia los últimos meses del año: Noviembre,
Diciembre, hace un inventario de caña disponible en las suertes, bajo los parámetros de
toneladas de caña por hectárea y por edad para determinar (mediante sus sistema de
información) la cantidad de caña disponible a ser cosechada en cada mes. Esta información es
pasada a la fábrica o planta que con base en ella, requerimientos de materia prima y paros
(por mantenimiento u otra razón programada) determina las toneladas diarias a moler.
Dado estos requerimientos, diarios por parte de la planta, el departamento de cosecha revisa y
ajusta diariamente, a primeras horas de la tarde, teniendo en cuenta la caña que queda en patio
y en campo, quemas accidentales, efectos de clima, etc. la programación diaria de corte del
día siguiente, determinando la hacienda a cortar y recursos a enviar (frente de alce).
A continuación se describe de manera detallada cada uno de los tres subprocesos, nombrados
anteriormente, que forman parte del proceso de cosecha para hacer mas claro los recursos
humanos y físicos que intervienen en ellos y el costeo respectivo en cada ingenio:
Subproceso de Corte: El corte en los ingenios de Colombia, y en particular en los dos
objetos de estudio, se lleva a cabo de dos maneras: de forma manual o mecánica.
El corte mecánico se realiza a través de una cuadrilla (denominados “frentes de alces”) de
personas que operan maquinas de corte, y alzadoras, además de tracto mulas que llevan la
caña directamente hasta el ingenio. Debido a los altos costos de inversión en la maquinaria los
ingenios en Colombia usan la figura de contratación de la cuadrilla entera para este tipo de
corte; además algunos ingenios por su ubicación en zonas de leyes especiales que obligan a
una mayor contratación de mano de obra propia del lugar, no usan o lo usan con menor
frecuencia. El corte realizado de manera mecánica ofrece una caña en trozos cortes pero una
mayor rapidez en su corte y por lo tanto menor tiempo desde la suerte hasta los patios del
7
ingenio lo cual ayuda a un mejor rendimiento de la caña en la producción de azúcar. El costo
asociado a este tipo de corte esta dado en una tarifa de pesos / ton-km.
El corte manual: se realiza a través de una mano de obra intensiva, por medio de las cuadrillas
(o “frentes de alce”), quienes cortan la caña directamente de la mata. Las ventajas de este tipo
de corte lo da los bajos costos de la mano de obra en nuestro país, que puede ser
subcontratada a través de cooperativas de trabajo o puede ser propia de cada ingenio, y el
tamaño de los bastones de caña que suelen ser más largos que en corte mecánico. Como
desventaja se presenta el mayor tiempo de corte de la suerte y por lo tanto mayor tiempo de
desplazamiento de la caña hasta los patios del ingenio. El costo de este tipo de corte se hace
por una tarifa de pesos/ton de caña.
Subproceso de Alce: consiste en levantar la caña que ha sido cortada de modo manual y
apilado en las “chorras”, por medio de una maquina mecánica llamada Alzadora, hasta el
transporte (tracto mulas o tractores) que llevaran la caña hasta el ingenio. Dentro de este
subproceso existen dos actividades más llamadas “Tapado de acequia” y “requisa”, las cuales
permiten tapar los surcos del terreno para que la maquina alzadora pueda entrar y recoger en
forma manual las cañas dejadas por la maquina alzadora respectivamente; La tarifa asociada a
esta actividad será en pesos/ton.
Subproceso de transporte: La actividad de transporte consiste en llevar la caña desde las
suertes, una vez ubicada en los vagones, en tractores o tractomulas hasta el ingenio. Vale la
pena anotar de nuevo, que solo se costea para las suertes cortadas de modo manual. Este
costo se asocia a una tarifa de pesos/ton dentro de un rango previo de distancias de la suerte al
ingenio.
3. MODELO PROPUESTO
3.1 Generalidades
El modelo propuesto como herramienta de decisión, para la solución de este problema,
buscará mediante la función objetivo asignar cada suerte a uno de los ingenios minimizando
los costos asociados a la cosecha (explicada detalladamente en el capitulo anterior), y a su vez
asignando el modo de corte, alce y transporte que cumpla con dicho objetivo dentro de cada
ingenio.La situación anterior se presenta en la Figura 1.
8
Figura 1. Imagen del Problema
El Modelo será un modelo de decisión estratégico, con un horizonte de planeación de un año,
con los siguientes supuestos:
1. Todas las suertes estarán disponibles a ser cosechadas una vez al año, lo que es
factible pues el ciclo de maduración (tiempo óptimo para ser cortada) oscila entre 10
y 12 meses.
2. La cantidad de caña a cosechar en cada suerte es conocida con anterioridad y al igual
que la distancia de la suerte al ingenio será la suministrada por cada ingenio.
3. Los costos de las actividades que comprende cada actividad de la cosecha: Corte, Alce
y Transporte deberán ser tomados, en caso de implementación del modelo, a partir de
la información suministrada por los ingenios.
3.2 Modelo Matemático
A continuación se presenta la notación y formulación matemática del problema de decisión a
través de un Modelo de Programación Lineal entera:
INDICES, CONJUNTOS Y SUBCONJUNTOS:
s∈ S
Suertes
s
∈ S inc
Suertes que pertenecen al ingenio A
s
∈ S cab
Suertes que pertenecen al Ingenio B
s
∈ S canj-inc
Suertes canjeables del ingenio A
s
∈ S canj-cab
Suertes canjeables del ingenio A
s
∈ S mec-inc
Suertes cosechadas mecánicamente por el ingenio A
i
∈I
Ingenios
i
∈ IS
Ingenios que pueden cortar la suerte s
c
∈C
Tipo de Corte
c
∈
Ci
Tipo de Corte del ingenio i
a
∈
A
Frentes de Alce
a
∈
Ai
Frentes de Alce del Ingenio i
a
∈ A si
Frentes de Alce que pueden ir a la suerte s del ingenio i
t
∈
T
Tipo de Transporte para llevar la caña desde la suerte al ingenio
t
∈
Ti
Tipo de Transporte del ingenio i
9
t
∈
Tsi
Tipo de Transporte usado en la suerte s por el Ingenio i
PARAMETROS:
Costos_Corte ci =
Costo de Corte de una tonelada de caña, por el modo de
corte “c” del ingenio “i” . [$/ton.]
Costo_Alce ai =
Costo de Alce de una tonelada de caña, por el frente de
Alce “a” del ingenio “i”. [$/ton.]
Costo_Transpor ti =
Costo de transporte de una tonelada de caña, del tipo de
transporte “t” del ingenio “i”. [$/ton-Km]
Caña-cosech s =
Cantidad de caña a cosechar de la suerte “s”. [ton]
d si =
Distancia de la suerte “s” al ingenio “i”. [Km]
∂i =
Índice promedio de rendimiento de la caña (sacarosa)
del ingenio “i” [adimensional]
Capacidad_Corte ci =
Capacidad de caña a cortar por cada tipo de corte “c” del
ingenio “i”. [ton/año]
Capacidad _Alce ai =
Capacidad de cada frente de alce “a” del ingenio “i”
[ton/año]
Capacidad_Transpor ti =
Capacidad de cada tipo de transporte “t” del ingenio “i”.
[ton/año]
Deman_Caña i =
Demanda anual de caña a moler del ingenio “i”.
[ton/año]
R 1=
Toneladas mínimas de azúcar, de diferencia, pactadas
entre los ingenios para llevar a cabo el canje de suertes.
R 2=
Toneladas máximas de azúcar, de diferencia, pactadas
entre los ingenios para llevar a cabo el canje de suertes.
VARIABLE:
Y sicat =
1 si la suerte “s” es cortada por el ingenio “i” del modo “c” por el alce
“a” y transportada, hasta el ingenio, en le tipo de transporte “t” .
0 de lo contrario
10
FUNCION OBJETIVO:
Minimizar (Costos de Cosecha de la suerte i) =
∑ ∑ ∑ ∑ ∑ [(Costos _ Corte
ci
)
+ Costos _ Alce ai × Caña _ Co sec h s
s ∈ S i ∈ I s c ∈C i a ∈ A si t ∈T si  A si
+ Costo _ Transporti × Caña _ Co sec h s × d si
] × Y sicat
La función objetivo, evalúa el costo de cosecha (corte, alce y transporte) asociado a cada
suerte en cada unos de los ingenios participantes, y dejará a cada ingenio (ya sean propias o
del otro ingenio) las suertes que minimicen su costo anual de cosecha.
RESTRICCIONES:
1. Capacidad de Corte:
∑ ∑ ∑ ∑ Caña _ Co sec h
s
* Y sicat ≤ Capacidad_Corte ci [ton/año]; ∀ c∈ C i
s ∈ S i ∈ I s a ∈ A si t ∈T si
El número total de suertes cortadas en alguno de los dos modos de corte para cada ingenio,
estará dado por la capacidad de los “frentes de alce” o cuadrillas que tenga cada ingenio
(restricción 1).
2. Capacidad de los frentes de Alce:
∑ ∑ ∑ ∑ Caña _ Co sec h s * Y sicat
≤ Capacidad _Alce ai [ton/año]; ∀ a ∈ A i .
s ∈ S i ∈ I s c ∈Ci t ∈T si
3. Capacidad de los tipos de transporte:
∑ ∑ ∑ ∑ Caña _ Co sec h
s
* Y sicat ≤ Capacidad_Transpor ti [ton/año]; ∀ t ∈ Ti
s ∈ S i ∈ I s c ∈Ci a ∈ A si
El número total de suertes que se podrán asignar a cada “frente de Acle” de cada ingenio,
estará dado por la capacidad de alce de los “frentes de alce” o cuadrillas y por la capacidad de
transporte asociados a estos, de cada ingenio; como se muestra en la restricción 2 y 3.
4. Demanda anual de molienda:
∑ ∑ ∑ ∑ Caña _ Co sec h s * Y sicat
≥ Deman_Caña i [ton/año]; ∀ i ∈ I
s ∈ S c ∈Ci a ∈ Ais t ∈Tis
11
La restricción 4 permitirá que las suertes asignadas a cada ingenio satisfagan la demanda
anual de molienda establecida en la planeación estratégica de cada ingenio.
5. Ecuación de Balance (por rendimiento)
R1 ≤
∑ ∑ Caña _ cos ech s ∗ σ 1 ∗ Y sicat
-
s ∈ S inc i = 2
∑ ∑ Caña _ Co sec h s ∗ σ 2 ∗ Y sicat
≤ R2 [ton/año]; ∀ c ∈ C i ; ∀ a ∈ A i ; ∀ t ∈ T i.
s ∈ S cab i =1
La restricción 5 permite que si a un ingenio se le asigna para cosechar una suerte que no sea
propia, es decir ocurra el canje de suertes, esta suerte este dentro del rango permitido de
rendimiento de azúcar que se haya pactado entre los ingenios, de acuerdo a sus medidas o
índices de rendimiento.
6. Cada suerte solo puede ser cortada una vez al año:
∑ ∑ ∑ ∑Y
sicat
= 1 ; ∀ s ∈ S.
i ∈ I s c ∈C i a ∈ A si t ∈Ti
Debido a que el ciclo de maduración de la suerte oscila entre 10 y 12 meses, esta restricción
garantiza que la suerte solo será cortada una vez en el año,
7. Binarias:
Ysicat ∈
{0.1}.
Esta última restricción define el dominio de la variable de decisión.
4. CONCLUSIONES
Como modelo propuesto, se presenta una herramienta de decisión a mediano plazo, es decir
con un horizonte de planeación de un año, lo cual permite tener desde el inicio del año las
posibles suertes a canjear. Esto se convierte en una ventaja para cada ingenio, pues
dependiendo de las condiciones tanto climáticas o de orden publico o de la misma demanda
de caña, cada vez que se llegue al momento de la cosecha de dichas suertes se puede evaluar
si otros argumentos, que además de los costos, pueden validar o rechazar dicha decisión. Es
decir se podrá tener una base para una concertación entre los ingenios de las suertes a canjear.
El modelo propuesto, puede ser resuelto en software de fácil acceso y bajo costo, se puede
encontrar plataformas de solución a este tipo de modelos sin costo alguno para su acceso,
como por ejemplo el Neo Server. Lo que le daría al modelo una ventaja para ser aplicado en
los ingenios, además la exportación de los resultados a archivos de software comerciales
podrían permitir la elaboración de algunas otras herramientas que permitan hacer un análisis
mas preciso acerca de las suertes que entran en canje.
12
Como se puede observar el planteamiento del modelo matemático, por medio de conjuntos e
índices permite encontrar una solución ya sea haciendo uso de todas las suertes de cada
ingenio o de aquellas que se decidan de antemano ser canjeables. Como ejemplo: se podría
mirar con este modelo si aquellas suertes que hayan decido ser canjeadas de manera empírica,
considerando solo la distancia, resultan ser también canjeables teniendo en cuenta los otros
costos asociados a la cosecha. De no ser así los ingenios podrían evaluar cuales serian esas
otras razones por las cuales el “paradigma a cerca de costos vs. Distancia” podría ser
cambiado.
Lo anterior daría otros interesantes casos de investigación y planteamiento de herramientas
que permitan encontrar estas razones.
4. BIBLIOGRAFIA
[1] Historia de la Caña de Azúcar. http://www.jas-multimedia.con/webpages/procana/canazuc.htm.
Noviembre 2008.
[2] ESPINAL, CARLOS; MARTÍNEZ, HÉCTOR; ORTIZ, LILA; BELTRÁN LUZ. La Cadena de
Azúcar en Colombia una Mirada Global de su Estructura y Dinámica 1991-2005. Documento de trabajo
No. 56. Observatorio Agrocadenas. Marzo de 2005. p.1.
[3] Anexo Estadístico de la Agroindustria del azúcar en Colombia 2006. http://www.agrocadenas.gov.co.
Noviembre 2008.
[4] DÍAZ, Rosa María. Propuesta de un Modelo Matemático para la Secuenciación Óptima de la
Cosecha de la Caña de Azúcar. Tesis de Pregrado. Universidad del Valle. 2000.
[5] VIVEROS, CARLOS HERNÁN. Formulación de un Modelo de Asignación para Optimizar el
Proceso de Cosecha de la Caña de Azúcar. Tesis de Pregrado. Universidad del Valle. 1996.
[6] LOPEZ, ESTEBAN; MIQUEL, SILVIA Y M. PLA ARAGONES, LLUIS. Sugar Cane
Transportation in Cuba, a case study. European Journal of Operational Research. pp.1-12, 2005.
[7] MARRERO, FERNANDO; ASENCIO, JAVIER; ABREU, R; SÁNCHEZ, J. Gestión del
transporte de la caña de azúcar con óptica multicriterio. Centro Azúcar. Vol.2. pp. 81-84, 2001.
[8] INFANTE, RAMIRO; VÁZQUEZ, XIOMARA. Planificación eficiente del proceso de
recolección de la caña de azúcar. Economía y Desarrollo. Vol.129. No.2. pp. 98-101, 2001.
[9] IOANNOU, GEORGE. Streamlining the supply chain of the Hellenic sugar industry. Journal of
Food Engineering. Vol.70. pp.323-332,2005.
[10] HIGGINS, ANDREW ET AL. Optimising harvest date in sugar production: A case study for the
Mossman mil region in Australia. I. Development of operations research model and solution. Field Crops
Research. Vol. 57. p.153-162,1998.
[11] HIGGINS, ANDREW. Australian Sugar Mills Optimize Harvester Rosters to Improve
Production. Interfaces. Vol.32. No.3. May –June. p.15-25,2002.
[12] HIGGINS, ANDREW; MUCHOW, RUSELL C. Assessing the potential benefits of alternative
cane supply arrangements in the Australian sugar industry. Agricultural Systems. Vol. 76. p. 623 – 638, 2003.
[13] HIGGINS, ANDREW ET AL. Optimising harvest date in sugar production: A case study for the
Mossman mil region in Australia. I. Development of operations research model and solution. Field Crops
Research. Vol. 57. p.153-162, 1998.
[14] HIGGINS, Andrew. Australian Sugar Mills Optimize Harvester Rosters to Improve Production.
Interfaces. Vol. 32. No. 3. May – June, p. 15-25 ,2002.
[15] HIGGINS, ANDREW; MUCHOW, RUSELL C. Assessing the potential benefits of alternative
cane supply arrangements in the Australian sugar industry. Agricultural Systems. Vol. 76. p. 623 – 638, 2003.
[16] HIGGINS, ANDREW; ANTONY, GEORGE; SANDELL, GARY; DAVIES, I;
PRESTWIDGE, D; ANDREW, B. A framework for integrating a complex harvesting and transport system for
sugar production. Agricultural Systems. Vol. 82. pp. 99-115,2004.
[17] HIGGINS, ANDREW.; IAN DAVIES. A simulation model for capacity planning in sugarcane
transport. Computers an electronics in agriculture. Vol.47. p.85-102,2005.
[18] HIGGINS, ANDREW. Scheduling of road vehicles in sugarcane transport: A case study at an
Australian sugar mill. European Journal of Operational Research. Vol.170. p.987,2006.
[19] M. GRUNOW, H – O GÜNTHER, R WESTINNER. Supply optimizacion for the producction
of raw sugar. Internacional Journal of Production Economics. Vol. 110. p. 224-239, 2007.
13