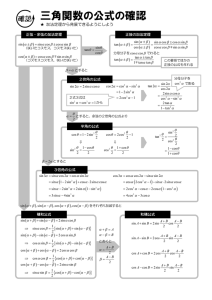
付録1（三角関数の加法定理関係の公式）

三角関数の加法定理関係の公式 (保存版)
3 倍角の公式
3α＝2α＋αとおいて、加法定理
(加法定理でβ＝2αとおく)
sin 3α＝ 3sinα－4sin3α
cos 3α＝ 4cos3α－3cosα
( sin2α＋cos2α＝ 1 )
次数を落とす公式
1－cos 2α
2
1
cos
2α
＋
cos2α＝
2
2 倍角の公式 (正弦･余弦)
sin 2α＝ 2 sinαcosα
cos 2α＝ cos2α－sin2α
＝ 1－2 sin2α＝ 2 cos2α－1
(∵ sin2α＋cos2α＝ 1)
2α＝θ α＝
tan
2 倍角の公式の右辺を
θ
θ
sin2 ＋cos2
(＝1)
2
2
で割り、その分母・分子を
θ
cos2
で割って
2
θ
sin
2
θ
tan
＝
を使う
2
θ
cos
2
sin2α＝
sinαcosα＝
三角関数の媒介変数表示
θ
とおいた
2
変形
β＝αとおく
sin 2α
2
θ
＝t とおくと
2
2t
sinθ＝
1＋t2
1－t2
cosθ＝
1＋t2
sinθ
tanθ＝
cosθ
2t
tanθ＝
1 －t 2
2α＝θ α＝
α
αを
に置き換える
2
α
α→
2
sin(α＋β)＝ sinαcosβ＋cosαsinβ
cos(α＋β)＝ cosαcosβ－sinαsinβ
半角の公式
1－cosα
α
sin2
＝
2
2
1
cos
α
＋
α
cos2
＝
2
2
βを－βに
置き換える
(β→－β)
sinθ
tanθ＝
cosθ
tan2
tan 2α＝
2 tanα
1－ tan2α
β＝αとおく
tanθ＝
正接の加法定理
sinθ
cosθ
(θ＝α＋β，α，β)
tanθ＝
正弦どうし、余弦どうしで
和、差を作り、2 で割る
とおく
正接の 2 倍角の公式
sin(－β)＝ －sinβ
cos(－β)＝ cosβ
cos(α－β)＝ cosαcosβ＋sinαsinβ
sin(θ＋α)＝ sinθcosα＋cosθsinα
sinθ
cosθ
(θ＝2α，α)
sin(α－β)＝ sinαcosβ－cosαsinβ
1－ cosα
α
＝
2
1＋ cosα
tanθ＝
θ
2
tan(α＋β)＝
tanα＋tanβ
1－tanαtanβ
βを－βに置き換える
tan(－β)＝ －tanβ
sinθ
cosθ
(θ＝α－β，α，β)
tan(α－β)＝
tanα－tanβ
1＋tanαtanβ
( cos(θ－α)＝ cosθcosα＋sinθsinα)
三角関数 (単振動) の合成
積 → 和･差 の公式 (積和公式)
a sinθ＋ b cosθ＝
sinαcosβ＝
a cosθ＋ b sinθ＝
ただし、cosα＝
sinα＝
a2＋b2 sin(θ＋α) (正弦)
a2＋b2 cos(θ－α) (余弦)
a
a2＋b2
b
a2＋b2
(a，b) y
α
a 2＋ b 2
O
x
1
{ sin(α＋β)＋sin(α－β)}
2
1
cosαsinβ＝
{ sin(α＋β)－sin(α－β)}
2
1
cosαcosβ＝
{ cos(α＋β)＋cos(α－β)}
2
1
sinαsinβ＝ － { cos(α＋β)－cos(α－β)}
2
和･差 → 積 の公式 (和積公式)
α＋β＝A
α－β＝B
とおくと
A＋B
2
A－B
β＝
2
α＝
A＋B
A－B
cos
2
2
A＋B
A－B
sinA－sinB ＝ 2 cos
sin
2
2
A＋B
A－B
cosA＋cosB ＝ 2 cos
cos
2
2
A＋B
A－B
cosA－cosB ＝ －2 sin
sin
2
2
sinA＋sinB ＝ 2 sin