三角関数の公式の確認
Anuncio

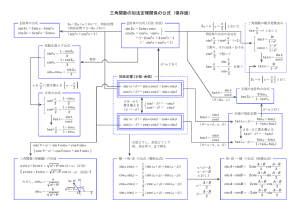
三角関数の公式の確認 ★ 加法定理から発展できるようにしよう 正弦・余弦の加法定理 正接の加法定理 sin sin cos cos sin (咲いたコスモス,コスモス咲いた) tan cos cos cos sin sin tan sin cos sin cos sin cos cos sin cos cos sin sin 分母分子を cos cos でわると tan (コスモスコスモス,咲いた咲いた) tan tan 1 tan tan この要領でほかの 正接の公式も作れる とすると 分母分子を 2倍角の公式 cos 2 cos 2 sin 2 sin 2 2sin cos 2 sin 2 cos で割る cos 2 2 sin cos cos 2 sin 2 2 tan 1 tan 2 tan 2 1 2sin 2 2 cos 2 1 2式3式は sin cos 1 から 2 2 とすると,余弦の2倍角の公式より 2 半角の公式 cos 1 2sin 2 2 cos 2 cos 2 sin 2 sin 2 2 tan 2 cos 2 2 1 cos 1 cos 1 2 2 1 cos 2 2 cos 2 1 cos 2 2 2 とすると 3倍角の公式 sin 3 sin cos 2 cos sin 2 cos 3 cos cos 2 sin sin 2 sin 1 2 sin cos 2sin cos cos 2 cos 2 1 sin 2 sin cos sin 2 sin 3 2sin 1 sin 2 2 cos3 cos 2 cos 1 cos 2 3sin 4sin 3 4 cos3 3cos 2 sin ,sin , cos , cos をそれぞれ加減すると 積和公式 和積公式 sin sin 2 sin cos 1 sin cos sin sin 2 sin sin 2 cos sin 1 cos sin sin sin 2 cos cos 2 cos cos 1 cos cos cos cos 2 cos cos 2sin sin 1 sin sin cos cos 2 A B とおくと A B 2 A B 2 sin A sin B 2sin A B A B cos 2 2 sin A sin B 2 cos A B A B sin 2 2 cos A cos B 2 cos A B A B cos 2 2 cos A cos B 2sin A B A B sin 2 2