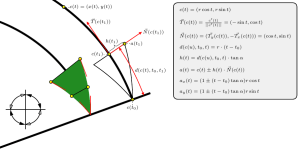
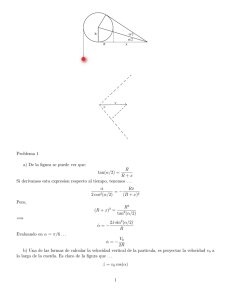
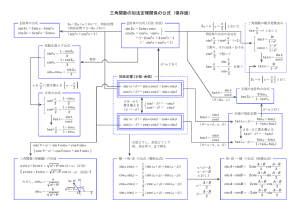
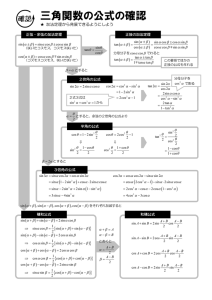
公式（三角関数）

公式（三角関数）− 1 −
公式（三角関数）
角の単位変換
απ
度→ラジアン： α =
(ラジアン)
180
◦
(
ラジアン→度： θ (ラジアン) =
180 θ
π
)◦
一般角の公式
sin(θ
+ 2nπ) = sin θ
cos(θ + 2nπ) = cos θ
tan(θ + 2nπ) = tan θ
(n は整数)
反角公式
sin(−θ)
= − sin θ
cos(−θ) = + cos θ
tan(−θ) = − tan θ
余角公式
(π
)
(π
)
sin
−
θ
=
cos
θ
cos
−
θ
= sin θ
2
2
tan
(π
2
−θ
)
=
1
tan θ
補角公式
sin(π
− θ) = + sin θ
cos(π − θ) = − cos θ
tan(π − θ) = − tan θ
π + θ の公式
sin(π
+ θ) = − sin θ
cos(π + θ) = − cos θ
tan(π + θ) = + tan θ
相互関係
sin θ
tan
θ=
cos θ
1
cos2 θ + sin2 θ = 1
1 + tan2 θ =
cos2 θ
1
1
+1 =
tan2 θ
sin2 θ
加法定理
sin(α
+ β) = sin α cos β + cos α sin β
sin(α − β) = sin α cos β − cos α sin β
cos(α + β) = cos α cos β − sin α sin β
cos(α − β) = cos α cos β + sin α sin β
tan(α + β) =
tan α + tan β
1 − tan α tan β
tan(α − β) =
tan α − tan β
1 + tan α tan β
公式（三角関数）− 2 −
倍角公式
sin
2θ = 2 sin θ cos θ
cos 2θ = cos2 θ − sin2 θ
tan 2θ =
cos 2θ = 2 cos2 θ − 1
2 tan θ
1 − tan2 θ
cos 2θ =
cos 2θ = 1 − 2 sin2 θ
1 − tan2 θ
1 + tan2 θ
sin 2θ =
2 tan θ
1 + tan2 θ
半角公式
1 − cos θ
2 θ
sin
=
2
2
cos2
θ
1 + cos θ
=
2
2
三倍角公式
sin
3θ = 3 sin θ − 4 sin3 θ
cos 3θ = 4 cos3 θ − 3 cos θ
3 sin θ − sin 3θ
4
3 cos θ + cos 3θ
3
cos θ =
4
sin3 θ =
積和公式
)
1(
sin
α cos β =
sin(α + β) + sin(α − β)
2
)
1(
cos(α + β) + cos(α − β)
cos α cos β =
2
)
1(
sin(α + β) − sin(α − β)
2
)
1(
sin α sin β = −
cos(α + β) − cos(α − β)
2
cos α sin β =
和積公式
α+β
α−β
sin
α + sin β = 2 sin
cos
2
2
α+β
α−β
cos α + cos β = 2 cos
cos
2
2
α+β
α−β
sin
2
2
α+β
α−β
cos α − cos β = −2 sin
sin
2
2
sin α − sin β =
合成
a sin θ + b cos θ = r sin(θ + α)
a cos θ + b sin θ = r cos(θ − α)
ただし， r =
√
a2 + b2
cos α =
a
,
r
sin α =
b
r
逆三角関数
θ = sin−1 y ⇐⇒ sin θ = y かつ −
π
π
5θ5
2
2
θ = cos−1 x ⇐⇒ cos θ = x かつ 0 5 θ 5 π
θ = tan−1 m ⇐⇒ tan θ = m かつ −
π
π
<θ<
2
2
2 cos