Ejercicios del Tema 1
Anuncio
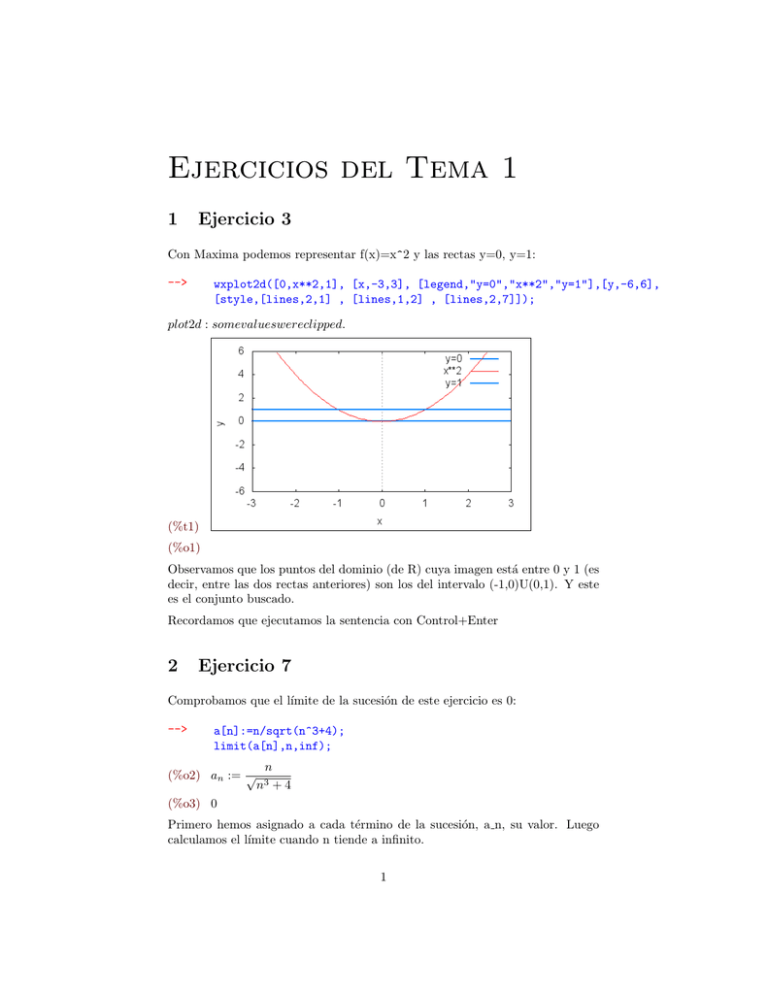
Ejercicios del Tema 1 1 Ejercicio 3 Con Maxima podemos representar f(x)=x^2 y las rectas y=0, y=1: --> wxplot2d([0,x**2,1], [x,-3,3], [legend,"y=0","x**2","y=1"],[y,-6,6], [style,[lines,2,1] , [lines,1,2] , [lines,2,7]]); plot2d : somevalueswereclipped. (%t1) (%o1) Observamos que los puntos del dominio (de R) cuya imagen está entre 0 y 1 (es decir, entre las dos rectas anteriores) son los del intervalo (-1,0)U(0,1). Y este es el conjunto buscado. Recordamos que ejecutamos la sentencia con Control+Enter 2 Ejercicio 7 Comprobamos que el lı́mite de la sucesión de este ejercicio es 0: --> a[n]:=n/sqrt(n^3+4); limit(a[n],n,inf); (%o2) an := √ n n3 +4 (%o3) 0 Primero hemos asignado a cada término de la sucesión, a n, su valor. Luego calculamos el lı́mite cuando n tiende a infinito. 1 3 Ejercicio 8 Comprobamos que el lı́mite de esta sucesión es 2. Primero limpiamos la memoria, para evitar problemas al llamar a[n] a esta sucesión. A continuación, definimos la sucesión a[n] y calculamos el lı́mite: --> kill(all); (%o0) done --> a[n]:=sqrt(16*n^4-4)/(n*sqrt(4*n^2+5)); limit(a[n],n,inf); √ 16 n4 − 4 (%o1) an := √ n 4 n2 + 5 (%o2) 2 4 Ejercicio 9 Procedemos como en los ejercicios anteriores: --> kill(all); a[n]:=sqrt(n^2+4*n+8)-n; limit(a[n],n,inf); (%o0) done (%o1) an := p n2 + 4 n + 8 − n (%o2) 2 5 Ejercicio 12 Calculamos el lı́mite como en los ejercicios anteriores: --> kill(all); a[n]:=((5*n+2)/(5*n+3))^(3*n+1); limit(a[n],n,inf); (%o0) done (%o1) an := 5n + 2 5n + 3 3 n+1 3 (%o2) e− 5 2 6 Ejercicio 13 Definimos el términos general de la sucesión a n y calculamos su lı́mite: --> kill(all); a[n]:=((n^4-n+1)/(2*n^4+n-2))^((n^2)/(n+1)); limit(a[n],n,inf); (%o0) done (%o1) an := n4 − n + 1 2 n4 + n − 2 n2 n+1 (%o2) 0 7 Ejercicio 14 Definimos,como habitualmente, el término general de la sucesión y calculamos su lı́mite: --> kill(all); a[n]:=n^(1/n); limit(a[n],n,inf); (%o0) done 1 (%o1) an := n n (%o2) 1 8 Ejercicio 15 El lı́mite de la sucesión de este ejercicio no es sencillo de calcular. Podemos definir la suma con sum e intentar calcular su valor. --> kill(all); t[i]:=(i+1)^i/i^(i-1); a[n]:=(sum(t[i],i,1,n))/n^2; limit(a[n],n,inf); (%o0) done (%o1) ti := (%o2) an := (i + 1) ii−1 Pn i i=1 ti n2 3 (%o3) Pn i1−i (i+1)i i=1 n2 n− > ∞ lim P 1−i (i+1)i n2 →f rac n i=1 i Sin embargo, no obtenemos ningún resultado. Pero Maxima nos puede ayudar cuando aplicamos el criterio de Stolz, para calcular el lı́mite que resulta: --> limit((((n+1)^n)/n^(n-1))/(2*n-1),n,inf); (%o4) e 2 9 Ejercicio 19 No es sencillo saber si una serie es convergente, y mucho menos conocer el valor de la suma de sus términos. Sin embargo, existen criterios que nos ayudan a decidir su carácter. Maxima nos puede ayudar en parte: puede calcular la suma de algunas series y siempre podemos aplicar algún criterio de convergencia. En este ejercicio, vamos a calcular el lı́mite que resulta de aplicar el criterio de cociente: --> kill(all); a[n]:=((n+1)^n)/((2*n-1)*n^(n-1)); limit(a[n],n,inf); (%o0) done n (%o1) an := (n + 1) (2 n − 1) nn−1 e 2 Este valor coincide con el que se calcula en el libro. Pero nótese que para el trabajo principal (¡darse cuenta de qué criterio hay que aplicar y hacerlo!) Maxima no nos ayuda. Hya algunas series cuyo valor conoce Maxima.Un ejemplo es el siguiente: (%o2) --> sum(1/n^2,n,1,inf),simpsum; (%o3) π2 6 10 Ejercicio 20 Como en el ejercicio anterior, hay que aplicar un criterio (en este caso, el de la raı́z), y Maxima nos ayuda con el lı́mtie que resulta: 4 --> kill(all); a[n]:=((n^(log(n)/n))/log(n)); limit(a[n],n,inf); (%o0) done log(n) n n (%o1) an := log (n) (%o2) 0 El cálculo de este lı́mite, resuelto fácilmente con Maxima, en el libro resulta laborioso. 11 Ejercicio 24 Maxima nos puede ayudar a factorizar los polinomios: --> kill(all); factor(x^2-x); factor(x^2+2*x-3); (%o0) done (%o1) (x − 1) x (%o2) (x − 1) (x + 3) También podı́amos haber simplificado directamente la expresión: --> ratsimp((x^2-x)/(x^2+2*x-3)); x x+3 Además, nos da directaente el lı́mite: (%o3) --> limit(((x^2-x)/(x^2+2*x-3)),x,1); (%o4) 1 4 12 Ejercicio 25 Hacemos como en los ejercicios anteriores: 5 --> kill(all); limit((log(x))/(log(4*x^4)),x,inf); (%o0) done (%o1) 13 1 4 Ejercicio 26 El lı́mite se puede calcular directamente, de forma similar a como se calcula el lı́mite se sucesiones: --> kill(all); limit(((x+1)/(x-1))^x,x,inf); (%o0) done (%o1) e2 14 Ejercicio 27 El calculo de ası́ntotas con Maxima se hace a través de la determinación de los lı́mites. Primero definimos la función y la llamamos f(x): --> kill(all); f(x):=(x^2+1)/(x^2-1); (%o0) done x2 + 1 x2 − 1 En este ejercicio, como en el libro, comenzamos con las ası́ntotas horizontales, que son los lı́mites cuando x tiende a infinito y menos infinito: (%o1) f (x) := --> limit(f(x),x,inf); limit(f(x),x,-inf); (%o2) 1 (%o3) 1 Como este lı́mite es 1, la recta y=1 es una ası́ntota horizontal. Una función tiene ası́ntotas verticales si cuando x tiende a un punto, entonces el lı́mite de la función es +infinito o -infinito. Para funciones que son una fracción, esto 6 ocurre cuando el denominador es 0. Por eso, calculamos primero las raı́ces del denominador: --> solve(x^2-1); (%o4) [x = −1, x = 1] Las raı́ces del denominador nos dicen donde buscar las ası́ntotas verticales. Hay que calcular los lı́mites de f(x) cuando x tiende a estos valores, pero por la derecha y por la izquierda: --> limit(f(x),x,1,plus); (%o5) ∞ --> limit(f(x),x,1,minus); (%o6) −∞ --> limit(f(x),x,-1,plus); (%o7) −∞ --> limit(f(x),x,-1,minus); (%o8) ∞ Como estos lı́mites son infinito o menos infinito, las rectas x=1,x=-1 son ası́ontotas verticales. Buscamos ası́ntotas oblicuas, calculando el lı́mite de f(x)/x cuando tiende a infinito y menos infinito: --> limit(f(x)/x,x,inf); limit(f(x)/x,x,-inf); (%o9) 0 (%o10) 0 Como este lı́mite es 0, significa que la ası́ntota oblicua tiene pendiente 0, es decir, es una ası́ntota horizontal. --> wxplot2d([f(x),1], [x,-5,5],[y,-10,10]); plot2d : somevalueswereclipped. 7 (%t11) (%o11) 15 Ejercicio 28 El cálculo de ası́ntotas con Maxima se hace a través de la determinación de los lı́mites. Primero definimos la función y la llamamos f(x): --> kill(all); f(x):=(x^3+2*x^2-1)/(x^2-4); (%o0) done x3 + 2 x2 − 1 x2 − 4 Comenzamos con las ası́ntotas horizontales: (%o1) f (x) := --> limit(f(x),x,inf); limit(f(x),x,-inf); (%o2) ∞ (%o3) −∞ Con estos resultados, no hay ası́ntotas horizontales. Continuamos con las ası́ntotas verticales. Buscamos las raı́ces del denominador: --> solve(x^2-4); (%o4) [x = −2, x = 2] Estos puntos son los candidatos a ası́ntotas verticales: 8 --> limit(f(x),x,2,plus); limit(f(x),x,2,minus); limit(f(x),x,-2,plus); limit(f(x),x,-2,minus); (%o5) ∞ (%o6) −∞ (%o7) ∞ (%o8) −∞ Observamos que tiene dos ası́ntotas verticales. Terminamos con las oblicuas: --> limit(f(x)/x,x,inf); limit(f(x)/x,x,-inf); (%o9) 1 (%o10) 1 Como estos lı́mties valen 1, sabemos que hay ası́ntotas oblicuas. Para encontrar su ecuación, nos falta el valor de la coordenada en el origen, que son los siguientes lı́mites: --> limit(f(x)-x,x,inf); limit(f(x)-x,x,-inf); (%o11) 2 (%o12) 2 Por eso, sólo hay una ası́ntota oblı́cua y es y=x+2. Finalmente, representamos la función: --> wxplot2d([f(x),x+2], [x,-5,5], [y,-30 ,30]); plot2d : somevalueswereclipped. 9 (%t13) (%o13) 16 Ejercicio 30 Comenzamos definiendo la función: --> kill(all); f(x):=x*cos(1/x); (%o0) done (%o1) f (x) := x cos 1 x Ahora calculamos su lı́mite, cuando x tiende a 0: --> limit(f(x),x,0); (%o2) 0 Podemos representar gráficamente la función. Vamos a hacerlo para que la salida sea una nueva ventana, porque ası́ nos podremos aproximar y alejar de la gráfica a capricho. --> wxplot2d([f(x)], [x,-5,5])$ plot2d : expressionevaluatestonon−numericvaluesomewhereinplottingrange. 10 (%t3) 17 Ejercicio 31 Primero definimos f(x) y luego calculamos su lı́mtie cuando x tiende a 2: --> kill(all); f(x):=(x^3-8)/(x-2); limit(f(x),x,2); (%o0) done (%o1) f (x) := x3 − 8 x−2 (%o2) 12 Nótese que se podı́a haber simplificado directamente con: --> ratsimp(f(x)); (%o3) x2 + 2 x + 4 18 Ejercicio 32 Estudiamos el lı́mite: --> kill(all); limit(exp(-1/(1+x)^2),x,-1); (%o0) done (%o1) 0 11 Aunque no sea continua, podemos definir a trozos la función y representarla: --> f(x):=if x=-1 then e^(-0.25) else exp(-1/(1+x)^2); ! −1 −0.25 (%o2) f (x) := ifx = −1thene elseexp 2 (1 + x) --> wxplot2d([f(x)], [x,-5,5])$ (%t3) Note que no se aprecia la discontinuidad, al ser sólo en un punto. 19 Ejercicio 33 Podemos componer funciones de la forma natural: --> kill(all); f(x):=abs(x); g(x):=if x=-1 then e^(-0.25) else exp(-1/(1+x)^2); g(f(x)); (%o0) done (%o1) f (x) := |x| (%o2) g (x) := ifx = −1thene (%o3) e −0.25 elseexp 1 − (|x|+1) 2 La representamos y lo vemos: 12 ! −1 (1 + x) 2 --> wxplot2d([f(x)], [x,-5,5])$ (%t4) 20 Ejercicio 39 El método de la bisección está implementado en Maxima. Sin embargo, no se permite al usuario controlar el número de iteraciones. El comando que se utiliza es find root. --> find_root (x^3-3,x,0,4); (%o5) 1.442249570307408 21 Ejercicio 43 De forma genérica, no es posible calcular lı́mites de sucesiones de funciones con Maxima. Si lo intentamos en este ejercicio, resulta: --> kill(all); f(n,x):=((1-x)^n)*sin(2*%pi/x); limit(f(n,x),n,inf); (%o0) done 2π x n 2π lim n− > ∞ sin x (1−x)n →(1−x) n (%o1) f (n, x) := (1 − x) sin (%o2) Sin embargo, vamos a representar las primeras funciones de la sucesión: 13 --> wxplot2d([f(1,x),f(2,x),f(3,x),f(4,x)], [x,-1,1])$ plot2d : expressionevaluatestonon−numericvaluesomewhereinplottingrange.plot2d : expressionevaluatestonon − numericvaluesomewhereinplottingrange.plot2d : expressionevaluatestonon − numericvaluesomewhereinplottingrange.plot2d : expressionevaluatestonon − numericvaluesomewhereinplottingrange. (%t8) 22 Ejercicio 45 En este ejercicio, sı́ es posible calcular el lı́mite de la sucesión de funciones: --> kill(all); f(n,x):=x/(2*n+1); limit(f(n,x),n,inf); (%o0) done (%o1) f (n, x) := x 2n + 1 (%o2) 0 23 Ejercicio 50 Si intentamos calcular directamente el lı́mite, vemos que no es posible: --> kill(all); f(n,x):=exp(-1/n^2)*x^n; sum(f(n,x),n,1,inf); (%o0) done 14 (%o1) f (n, x) := exp (%o2) ∞ X −1 n2 xn 1 e− n2 xn n=1 Tampoco permite calcular el lı́mite si x=1 0 x=-1: --> (%o3) sum(f(n,-1),n,1,inf); ∞ X 1 e− n2 (−1) n n=1 Pero sin embargo, sı́ podemos ayudar a determinar el radio de convergencia, con el criterio del cociente: --> limit(exp(-1/n^2)/(exp(-1/(n-1)^2)),n,inf); (%o4) 1 15









