4 Modelos del campo usando armónicos esféricos
Anuncio
4 Modelos del campo usando armónicos esféricos
– p. 1
4.1 Introducción
Se pueden usar las observaciones para medir el campo geomagnético a ubicaciones
específicas.
Hay que considerar las ubicaciones (r, θ, φ) donde no hay mediciones.
Idealmente, queremos usar todas las observaciones geomagnéticas juntas para definir un
modelo del campo geomagnético global.
Este modelo nos dará la mejor estimación posible a cualquier latitud, longitud y altitud.
Para la construcción de un modelo del campo global, usaremos funciones con una geometría
esférica ortogonales que suman a dar el potencial magnético.
– p. 2
4.2.1 Funciones periódicas en una dimensión
Cualquier función f (t), que es periódica sobre un intervalo T , puede ser representada por
una suma de sinusoides con un número de onda entero m.
Este técnico es comúnmente conocido como una serie de Fourier:
f (t) =
∞ X
m=0
2πmt
2πmt
+ bm sin
am cos
T
T
Las funciones sinusoidales son ortogonales. Es decir que la integración de su producto sobre
el intervalo T es cero, a menos que su números de ondas son idénticos:
Z
T
0
T
2 , si m = n 6= 0;
2πmt
2πnt
cos
cos
dt =
0 , si m 6= n;
T
T
T , si m = n = 0;
Usando esta ortogonalidad, podemos fácilmente evaluar las coeficientes am y bm si sabemos
la función f (t).
– p. 3
4.2.2 La función para longitud
Imagínese la función periódica f (t) alrededor de un círculo de longitud. t es equivalente a la
longitud (φ), con T = 2π, y entonces:
f (φ) =
∞
X
am cos mφ + bm sin mφ
m=0
Si la serie representa la función de longitud a cualquier latitud, entonces:
f (θ, φ) =
∞
X
am (θ) cos mφ + bm (θ) sin mφ
m=0
Debemos encontrar una función para representar la co-latitud (θ)
– p. 4
4.2.3 La función para latitud
Las funciones de co-latitud en una esfera no necesitan ser periódicas como las funciones de
longitud.
Entonces una base sinusoidal no es una buena elección.
También, existen problemas porque las funciones latitudinales se convergen en los polos.
Para la representación de variaciones latitudinales en una esfera necesitamos una base
completa de funciones ortogonales. En principio, muchas funciones están posibles.
En muchos problemas físicos que usan geometría esférica (incluyendo la ecuación de
Laplace, resuelta por la separación de variables), la elección natural son las funciones de
Legendre para representar las variaciones latitudinales en una esfera.
– p. 5
4.2.4 Las funciones asociadas de Legendre
Las funciones asociadas de Legendre son definidas matemáticamente por la relación:
Pl,m (µ) = (1 −
m
µ2 ) 2
m
∂
∂µm
l
1 d
2
l
(µ
−
1)
l!2l dµl
!
donde µ = cos θ
l es el grado del polinomio, corresponde al número de líneas nodales en la latitud (cuando el
orden m = 0).
– p. 6
4.2.5 La definición de armónicos esféricos
Con una suma de las funciones asociadas de Legendre para la representación de una
variación latitudinal, obtenemos la siguiente representación para una función en una
superficie esférica:
f (θ, φ) =
∞ X
l
X
m
(glm cos mφ + hm
l sin mφ)Pl (θ)
l=0 m=0
Cada (l, m) representa una armónica esférica individual.
Para m > 0 cada armónica esférica consiste de una parte coseno y una parte seno.
– p. 7
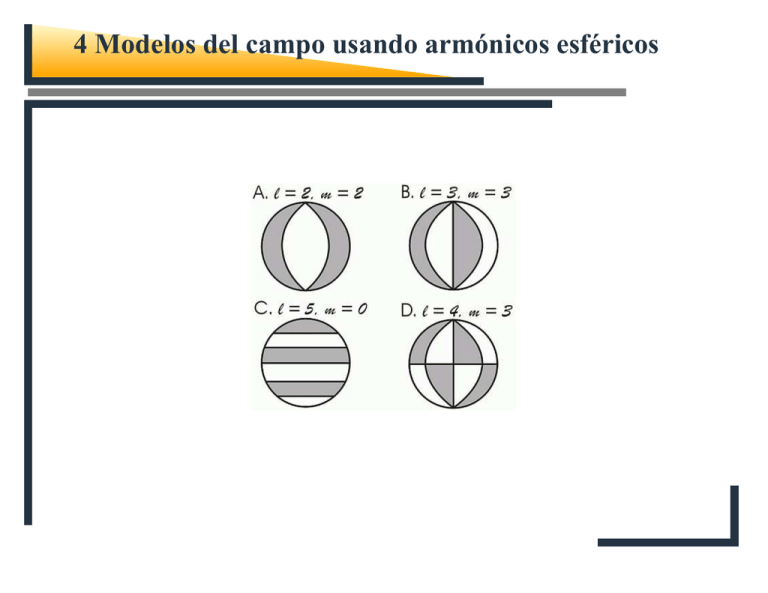
4.2.6 Las propiedades de armónicos esféricos
Los armónicos están cero en (l − m) líneas de latitud y 2m líneas de longitud.
Si (l − m) es par, los armónicos están simétricos alrededor del plano ecuatorial.
Si (l − m) es inpar, los armónicos están antisimétricos alrededor del plano ecuatorial.
Existen (2l + 1) coeficientes para cada grado l.
http://www.bpreid.com/poas.php
– p. 8
4.2.7 La ortogonalidad de los armónicos esféricos
Similarmente a las sinusoidales en la serie de Fourier, los componentes de armónicos
esféricos están ortogonales:
Z
2π
0
Z
Z
2π
0
2π
0
Z
π
0
Z
Z
π
0
π
0
m
′
m′
cos mφPl (θ). cos m φPl′ (θ) sin θdθdφ
m
′
m′
sin mφPl (θ). sin m φPl′ (θ) sin θdθdφ
m
′
=
(
0 , si l 6= l′ o m 6= m′ ;
4π
′
′
(2l+1) , si l = l y m = m ;
=
(
0 , si l 6= l′ o m 6= m′ ;
4π
′
′
(2l+1) , si l = l y m = m ;
m′
sin mφPl (θ). cos m φPl′ (θ) sin θdθdφ = 0
Si multiplicamos cualquier función de interés en una superficie esférica por un armónico
esférico particular, y integramos sobre la esfera, la ortogonalidad de los armónicos nos deje
determinar las coeficientes glm y hm
l :
(
)
(
)
Z 2π Z π
(2l + 1)
cos
mφ
glm
f (θ, φ)Plm (θ)
sin θdθdφ
=
m
sin mφ
hl
4π
0
0
– p. 9
4.3.1 El campo geomagnético y armónicos esféricos
En regiones libres de las fuentes del campo (sin corrientes eléctricas), y dado que no existen
monopolos magnéticos (estable y macroscópico), entonces B = −∇V y ∇ · B = 0.
El potencial magnético para el campo magnético terrestre entonces cumple la ecuación de
Laplace en geometría esférica:
1 ∂
∇ V =
r ∂r
2
∂V
r
∂r
2
1
∂
+ 2
r sin θ ∂θ
∂V
sin θ
∂θ
1
∂2V
+ 2
=0
r sin2 θ ∂φ2
La solución general para el potencial magnético involucra los armónicos esféricos:
" a l+1 m
m
m
(gl cos mφ + hl sin mφ)Pl (θ)
V =a
r
l=1 m=0
#
l
r
m
m
m
+
(ql cos mφ + sl sin mφ)Pl (θ)
a
∞ X
l
X
Las coeficientes son conocidos como las coeficientes de Gauss, medidas en nT. El constante
a es el radio terrestre de referencia (6371 km).
– p. 10
4.3.2 El campo interno y el campo externo
Fuentes internas
z"
}|
{
∞
l
l+1
X X
a
m
(glm cos mφ + hm
V =a
l sin mφ)Pl (θ)
r
l=1 m=0
#
l
r
m
+
(qlm cos mφ + sm
l sin mφ)Pl (θ)
a
{z
}
|
Fuentes externas
Noten que tenemos dos expansiones de los armónicos esféricos en la solución general a la
ecuación de Laplace con geometría esférica.
Los campos asociados con las fuentes internas y las fuentes externas tienen una diferente
dependencia radial.
Entonces campos internos (por ejemplo del núcleo) y campos externos (por ejemplo de la
magnetosfera) pueden ser separados, si hay observaciones a diferentes alturas disponibles.
El campo interno es ∼97% del campo total observado en la superficie de la Tierra (excepto
cuando hay una tormenta magnética).
– p. 11
4.3.3 La relación entre armónicos y observaciones
Usando B = −∇V en geometría esférica, y la expresión para V usando armónicos
esféricos, podemos escribir los componentes del campo. Por ejemplo, Br (para el campo
interno, hasta grado L,) es:
l+2
L X
l
X
∂V
a
m
m
m
Br = −
(gl cos mφ + hl sin mφ)Pl (θ)
=
(l + 1)
∂r
r
l=1 m=0
Junto con expresiones similares para Bθ y Bφ , podemos construir las expresiones para las
componentes observables del campo:
X = −Bθ
Y = Bφ
Z = −Br
2
2
1
2
2
2 1
H = (Bθ + Bφ ) 2
F = (Bθ + Bφ + Br ) 2
π
π
−Br
donde −
I = tan−1
≤
I
≤
1
2
2
2)2
(Bθ2 + Bφ
B
φ
−1
donde − π ≤ D ≤ π
D = tan
−Bθ
– p. 12
4.3.4 Los polos geomagnéticos y el campo dipolar
El momento magnético del dipolo geomagnético a un radio a es:
mD
4πa3 q 0 2
=
(g1 ) + (g11 )2 + (h11 )2
µ0
mD mide la magnitud del dipolo (en unidades Am2 ).
La inclinación del dipolo en las direcciones meridional (θ) y azimutal (φ), relativo al eje
geográfico de la Tierra, es:
θD = cos
−1
−1
φD = cos
mzD
mD
= cos
−1
g01
q
1
1
1
2
2
2
(g0 ) + (g1 ) + (h1 )
mxD
p
(mxD )2 + (myD )2
!
−1
= cos
q
g11
(g11 )2 + (h11 )2
– p. 13
4.3.4 Los polos geomagnéticos y el campo dipolar
La figura muestra el eje dipolar de la Tierra debido a un modelo del campo geomagnético de
1990.
La componente dipolar explica un gran parte del campo magnético terrestre, pero las otras
componentes están muy relevantes para muchos estudios geofísicos.
El polo norte geomagnético es el polo del eje dipolar (donde el eje se cruza con la superficie
de la Tierra). El polo norte magnético es el punto en la Tierra donde I = 90◦ . Estos dos
polos son distintos.
– p. 14
4.4 El espectro de las armónicas esféricas
Se puede separar las partes del campo asociadas con el núcleo y la corteza.
La potencia del campo magnético, en una superficie esférica, asociada con el grado armónico
m 2
2l+4 Pl
m 2
)
)
+
(h
(g
l es (Lowes, 1974): Rl = a
l
l
m=0
r
Existen dos pendientes distintos, que indican dos fuentes internas con profundidades muy
diferentes.
Tomando l < 14 para el núcleo, y l > 14 para la corteza, las dos fuentes internas pueden
estar separados (parcialmente).
– p. 15
4.5.1 Propiedades del campo magnético de hoy
Modelos globales (usando armónicos esféricos) están hoy día derivados de los datos de
satélites y observatorios.
Los modelos globales del campo geomagnético incluyen:
1. IGRF = International Geomagnetic Reference Field: Derivado cada 5 años por la
colaboración internacional, disponible gratis y usado siempre en aplicaciones comerciales
(por ejemplo GPS). Ese campo de referencia consiste de los armónicos esféricos hasta grado
l = 13.
2. WMM = World Magnetic Model: Una colaboración EEUU/RU también publicado cada 5 años.
– p. 16
4.5.2 La declinación D
– p. 17
4.5.3 La inclinación I
– p. 18
4.5.4 La intensidad horizontal H
– p. 19
4.5.5 Componente al norte X
– p. 20
4.5.6 Componente al este Y
– p. 21
4.5.7 Componente vertical Z
– p. 22
4.5.8 La intensidad total F
– p. 23
4.6 Interrupciones de satélites
– p. 24
4.7 Conclusión
Desviaciones significativas de un campo dipolar son observadas.
La mayor intensidad es cerca Canadá, en Siberia y entre Antártica y Australia.
La menor intensidad es cerca Sudamérica / El Atlántico del sur (South Atlantic Anomaly:
SAA).
El campo vertical generalmente es más fuerte que el campo horizontal. Pero cerca el
ecuador, el campo horizontal tiene mayor intensidad.
Los armónicos esféricos son útiles para representar el campo.
Se puede separar el campo del núcleo y el campo de la corteza usando una representación
de armónicos esféricos para el campo.
La determinación precisa de las coeficientes de Gauss glm y hm
l estará en la próxima clase.
– p. 25







