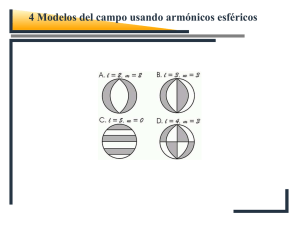
MMF - Academia Ciencias Galilei

Para el interior de la esfera, debemos solucionar la ecuación de Poisson para el potencial 𝜙,
que tiene la forma:
∇2 𝜙(𝑟) = 𝜌(𝑟)
(1)
El signo menos que introduce la teoría electromagnética puede omitirse, ya que es absorbido
por la función de densidad de carga volumétrica, siendo así la ecuación (1) una forma más
general.
⃗⃗⃗) es soluciòn de (1) en 𝑟′
⃗⃗⃗, con lo que
Ahora, supongamos que la función de Green 𝐺(𝑟⃗, 𝑟′
podemos escribir:
∇2 𝐺(𝑟⃗, ⃗⃗⃗⃗
𝑟 ′ ) = 𝛿(𝑟⃗ − ⃗⃗⃗⃗
𝑟′)
(2)
Es necesario hallar la forma de 𝛿(𝑟⃗, ⃗⃗⃗⃗
𝑟 ′ ) en coordenadas esféricas, para ello, notemos que:
∞
∫ 𝛿(𝑟 − 𝑟 ′ )𝑑𝑟 = 1
0
2𝜋
∫ 𝛿 (𝜑 − 𝜑′ )𝑑𝜑 = 1
0
𝜋
∫ 𝛿(𝜃 − 𝜃′)𝑑𝜃 = 1
{
0
Con lo que:
2𝜋
∞
∫ 𝛿(𝑟⃗ −
⃗⃗⃗⃗
𝑟 ′ )𝑑𝑉
= 1 = ∫ 𝛿(𝑟 − 𝑟
𝑉
′ )𝑑𝑟
0
· ∫ 𝛿 (𝜑 − 𝜑
𝜋
′ )𝑑𝜑
· ∫ 𝛿(𝜃 − 𝜃′)𝑑𝜃
0
0
Teniendo en cuenta que en coordenadas esféricas 𝑑𝑉 = 𝑟 2 𝑠𝑒𝑛𝜃𝑑𝑟𝑑𝜃𝑑𝜑, podemos escribir la
última igualdad como:
∫ 𝛿(𝑟⃗ − ⃗⃗⃗⃗
𝑟 ′ )𝑑𝑉 = ∫
𝑉
𝑉
𝛿(𝑟 − 𝑟 ′ )𝛿(𝜃 − 𝜃′)𝛿(𝜑 − 𝜑′ )
𝑑𝑉
𝑟′2 𝑠𝑒𝑛𝜃′
Y ya que el volumen 𝑉 es arbitrario:
𝛿(𝑟⃗ − ⃗⃗⃗⃗
𝑟′) =
𝛿(𝑟 − 𝑟 ′ )𝛿(𝜃 − 𝜃′)𝛿(𝜑 − 𝜑′ )
𝑟′2 𝑠𝑒𝑛𝜃′
Por lo que (2) toma la forma:
𝛿(𝑟−𝑟
∇2 𝐺(𝑟⃗, ⃗⃗⃗⃗
𝑟 ′) =
′ )𝛿(𝜃−𝜃′)𝛿(𝜑−𝜑′ )
𝑟 ′2 𝑠𝑒𝑛𝜃′
De la Relación de Completes para Armónicos Esféricos, sabemos que:
(3)
∞
+𝑙
𝛿(𝜃 − 𝜃′)𝛿(𝜑 − 𝜑 ′ )
= ∑ ∑ 𝑌𝑙𝑚 (𝜃, 𝜑)𝑌𝑙∗𝑚 (𝜃′, 𝜑′)
𝑠𝑒𝑛𝜃′
𝑙=0 𝑚=−𝑙
Con lo que (3) se torna en:
∞
+𝑙
1
∇ 𝐺(𝑟⃗, ⃗⃗⃗⃗
𝑟 ′ ) = 2 𝛿(𝑟 − 𝑟′ ) ∑ ∑ 𝑌𝑙𝑚 (𝜃, 𝜑)𝑌𝑙∗𝑚 (𝜃′, 𝜑′)
𝑟′
2
(4)
𝑙=0 𝑚=−𝑙
Al ser los Armónicos Esféricos un set completo de funciones, podemos expandir
𝐺(𝑟⃗, ⃗⃗⃗⃗
𝑟 ′ ) en dicho set de la forma:
𝐺(𝑟⃗, ⃗⃗⃗⃗
𝑟 ′ ) = ∑ 𝐺𝑙𝑚 (𝑟⃗, ⃗⃗⃗⃗
𝑟 ′ )𝑌𝑙𝑚 (𝜃, 𝜑)
(5)
𝑙,𝑚
Además, teniendo en cuenta el Laplaciano en coordenadas esféricas y que para los Armónicos
Esféricos se cumple
1 𝜕
𝜕𝑌
1 𝜕2𝑌
(𝑠𝑒𝑛𝜃 ) +
= −𝜆𝑌,
𝑠𝑒𝑛𝜃 𝜕𝜃
𝜕𝜃
𝑠𝑒𝑛𝜃 2 𝜕𝜃 2
𝑐𝑜𝑛 𝜆 = 𝑙(𝑙 + 1)
Podemos escribir (5) de la forma:
∞
+𝑙
1 𝑑2
𝑙(𝑙 + 1) 𝑚
1
∗𝑚
(𝑟𝐺
)
(
)
∑[
−
]
𝑌
𝜃,
𝜑
=
𝛿(𝑟 − 𝑟 ′ ) ∑ ∑ 𝑌𝑚
𝑚𝑙
𝑙
𝑙 (𝜃, 𝜑)𝑌𝑙 (𝜃′, 𝜑′)
2
𝑟 𝑑𝑟 2
𝑟2
𝑟′
(6)
𝑙=0 𝑚=−𝑙
𝑙,𝑚
Como los 𝑌𝑙𝑚 (𝜃, 𝜑) son orto normales según el argumento angular, en el término
derecho de (6) sólo sobrevive el factor para el cual 𝜑 = 𝜑 ′ , 𝜃 = 𝜃′, así, podemos
escribir :
1 𝑑2
𝑙(𝑙 + 1) 𝑚
1
∗𝑚 ′
′
(𝑟𝐺𝑚𝑙 ) −
[
] 𝑌𝑙 (𝜃, 𝜑) = 2 𝛿(𝑟 − 𝑟 ′ )𝑌𝑚
𝑙 (𝜃, 𝜑)𝑌𝑙 (𝜃 , 𝜑 )
2
2
𝑟 𝑑𝑟
𝑟
𝑟′
Simplificando:
1 𝑑2
𝑙(𝑙 + 1)
1
′
′
(𝑟𝐺𝑚𝑙 ) −
[
𝐺𝑚𝑙 ] = 2 𝛿(𝑟 − 𝑟 ′ )𝑌∗𝑚
𝑙 (𝜃 , 𝜑 )
2
2
𝑟 𝑑𝑟
𝑟
𝑟′
(7)
Que es una ecuación diferencial para la parte radial y angular. Podemos hace una
separación de variables de la forma:
𝐺𝑙𝑚 = 𝑔𝑙 (𝑟, 𝑟 ′ )𝑌𝑙∗𝑚 (𝜃 ′ , 𝜑 ′ )
(8)
Reemplazando (8) en (7) se obtiene, luego de simplificar 𝑌𝑙∗𝑚 (𝜃 ′ , 𝜑 ′ ):
1 𝑑2
𝑙(𝑙 + 1)
1
[
(𝑟𝑔𝑙 (𝑟, 𝑟′ )) −
𝑔𝑙 (𝑟, 𝑟′ )] = 2 𝛿(𝑟 − 𝑟 ′ )
2
2
𝑟 𝑑𝑟
𝑟
𝑟′
(9)
Esta ecuación es una ecuación diferencial en una dimensión para la función de Green.
Para 𝑟 ≠ 𝑟′, el lado derecho de (9) es cero, así que su solución en general es de la
forma:
𝑔𝑙 = 𝛼𝑟 𝑙 +
𝛽
𝑟 𝑙+1
Pero como hay puntos mayores y menores que 𝑟’, las constantes deben ser distintas,
así, tenemos que para cada región:
𝐵
𝐴𝑟 𝑙 + 𝑙+1 ,
𝑟
𝑔𝑙 = {
𝐷
𝐶𝑟 𝑙 + 𝑙+1 ,
𝑟
𝑟 < 𝑟′
(10)
𝑟 > 𝑟′
Para 𝑟 = 0, la función debe ser finita, por lo tanto 𝐵 = 0. Para 𝑟 = 𝑎 (radio de la
esfera), la función vale cero (ya que es un punto distinto de 𝑟’), luego:
𝐶𝑎𝑙 +
𝐷
=0
𝑎𝑙+1
Reemplazando estos resultados en (10):
𝐴𝑟 𝑙 ,
𝑟 < 𝑟′
2𝑙+1
𝑔𝑙 = {
𝑎
𝐶(𝑟 𝑙 − 𝑙+1 ),
𝑟
(11)
𝑟 > 𝑟′
Es necesario hallar la solución para 𝑟 = 𝑟’. Pare ello usamos las condiciones que debe
cumplir la función de Green y su derivada, en una vecindad de 𝑟′, que están dadas por:
′
𝑟=𝑟 +𝜖
𝑑
1
(𝑟𝑔𝑙 )]
=
𝑑𝑟
𝑝(𝑟′)
𝑟=𝑟 ′ −𝜖
𝑔𝑙 (𝑟 ′ + 𝜖, 𝑟) = 𝑔𝑙 (𝑟 ′ − 𝜖, 𝑟)
Con 𝑝(𝑥) = 𝑟’. Computando estas condiciones y haciendo que 𝜖 tienda a cero,
teniendo en cuenta que para 𝑟 ′ + 𝜖 los 𝑟 son mayores que 𝑟’ y que para 𝑟 ′ − 𝜖 son
menores y tomando las soluciones de (11), obtenemos:
𝐴𝑟′𝑙 = 𝐶 [𝑟′𝑙 −
𝑎2𝑙+1
]
𝑟′𝑙+1
𝑎2𝑙+1
1
𝑙
𝐶 [(𝑙 + 1)𝑟 + 𝑙 𝑙+1 ] − 𝐴(𝑙 + 1)𝑟 ′ =
𝑟′
𝑟′
{
′𝑙
Al resolver este sistema para 𝐴 y 𝐶:
𝐶=
𝐴=
𝑟′𝑙
(2𝑙 + 1)𝑎2𝑙+1
𝑟′𝑙
𝑎 2𝑙+1
[1
−
(
)
]
(2𝑙 + 1)𝑎2𝑙+1
𝑟′
Por lo tanto, (11) toma la forma:
𝑎 2𝑙+1
[1
−
(
)
],
𝑟 𝑟′
𝑟′
𝑔𝑙 (𝑟, 𝑟′) =
{
𝑎 2𝑙+1
(2𝑙 + 1)𝑎2𝑙+1
[1 − ( )
],
𝑟
𝑙
𝑟 < 𝑟′
𝑙
(12)
𝑟 > 𝑟′
⃗⃗⃗) se obtiene al reemplazar (12) en (8) y esto luego reemplazarlo
Finalmente, la solución 𝐺(𝑟⃗, 𝑟′
en (5), con lo cual:
∞
𝐺(𝑟⃗, ⃗⃗⃗⃗
𝑟′)
+𝑙
′
∗𝑚
′
= ∑ ∑ 𝑔𝑙 (𝑟, 𝑟′)𝑌𝑚
𝑙 (𝜃, 𝜑)𝑌𝑙 (𝜃 , 𝜑 )
𝑙=0 𝑚=−𝑙
Teniendo en cuenta el Teorema de Adición de los Armónicos Esféricos:
∞
+𝑙
4𝜋
𝑃𝑙 (cos(Θ)) =
∑ ∑ 𝑌𝑙𝑚 (𝜃, 𝜑)𝑌𝑙∗𝑚 (𝜃 ′ , 𝜑 ′ )
2𝑙 + 1
𝑙=0 𝑚=−𝑙
Obtenemos:
∞
1
𝐺(𝑟⃗, ⃗⃗⃗⃗
𝑟′) =
∑(2𝑙 + 1)𝑔𝑙 (𝑟, 𝑟′)𝑃𝑙 (cos(Θ))
4𝜋
𝑙=0
Con Θ el ángulo entre 𝑟⃗ y ⃗⃗⃗⃗
𝑟′.
Por último, el potencial, según el Teorema de las Funciones de Green es:
𝑎
𝜑(𝑟) = ∫ 𝐺(𝑟⃗, ⃗⃗⃗⃗
𝑟 ′ ) 𝜌(𝑟′)𝑑𝑟′
0