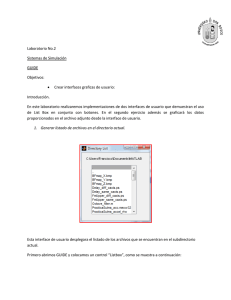
Untitled - Tesis Electrónicas UACh
Anuncio

II
III
Agradecimientos
Quiero dar las gracias a mis padres: Lina y Hugo por el enorme esfuerzo y
sacrificio que hicieron para darme la oportunidad de estudiar y por la confianza que me
han tenido siempre. Doy gracias también a mi familia, que de una u otra manera
contribuyeron y ayudaron en mi formación y en especial a mis tíos Feli y Silvia por su
apoyo y ayuda.
Le agradezco a don Roberto Cárdenas por darme la oportunidad de realizar mi
tesis con él y por la ayuda brindada durante este trabajo. También agradezco a los
profesores don Milton Lemarie y don Claudio Bastidas.
Finalmente, a todos aquellos que han hecho posible que este proceso haya tenido
tan satisfactorio término.
IV
Dedicatoria
A mis padres Lina y Hugo.
V
Índice
Resumen .............................................................................................................................................. 1
Summary ............................................................................................................................................. 2
Introducción ........................................................................................................................................ 3
Objetivo General ............................................................................................................................. 7
Objetivos Específicos ..................................................................................................................... 7
Metodología ........................................................................................................................................ 8
1.
Conceptos y principios básicos del mantenimiento..................................................................... 9
1.1.
2.
3.
Evolución histórica sobre el desarrollo de fallos ................................................................. 9
1.1.1.
Curva de Bañera o de Davies ...................................................................................... 9
1.1.2.
Curvas de Fallos actuales .......................................................................................... 11
1.2.
Confiabilidad ..................................................................................................................... 13
1.3.
Mantenibilidad .................................................................................................................. 15
1.4.
Disponibilidad ................................................................................................................... 16
Caracterización del potencial eólico.......................................................................................... 17
2.1.
Potencia contenida en el viento y potencia aprovechable ................................................ 18
2.2.
Curva de potencia de los aerogeneradores ........................................................................ 20
2.3.
Cálculo de potencia generada ........................................................................................... 21
Variables aleatorias continuas ................................................................................................... 22
3.1.
Variable aleatoria .............................................................................................................. 22
3.2.
Función densidad de probabilidad ..................................................................................... 23
3.3.
Función de distribución acumulada ................................................................................... 24
3.4.
Función de Confiabilidad o distribución acumulada complementaria .............................. 25
3.5.
Función de riesgo .............................................................................................................. 26
3.6.
Distribuciones de probabilidad continuas ......................................................................... 27
3.6.1.
Distribución Normal .................................................................................................. 28
3.6.2.
Distribución Log-Normal .......................................................................................... 31
3.6.3.
Distribución de Gamma............................................................................................. 33
3.6.4.
Distribución Rayleigh................................................................................................ 35
3.6.5.
Distribución Exponencial .......................................................................................... 36
3.6.6.
Distribución de Weibull ............................................................................................ 39
VI
4.
5.
Métodos de estimación de parámetros ...................................................................................... 44
4.1.
Máxima verosimilitud ....................................................................................................... 44
4.2.
Mínimos Cuadrados .......................................................................................................... 46
4.3.
Pruebas de bondad de ajuste .............................................................................................. 50
4.3.1.
Test de Kolmogorov-Smirnov ................................................................................... 50
4.3.2.
Prueba Chi-Cuadrado ................................................................................................ 55
4.3.3.
Niveles de confianza ................................................................................................. 58
Desarrollo del programa ............................................................................................................ 60
5.1.
MATLAB .......................................................................................................................... 60
5.2.
Tratamiento de datos ......................................................................................................... 61
5.2.1.
5.3.
7.
Funcionamiento del programa ........................................................................................... 63
5.3.1.
Diagramas de flujo de cada interfaz .......................................................................... 63
5.3.2.
Diagramas de flujo discriminados de acuerdo a su función ...................................... 65
5.4.
6.
Nivel de significancia ................................................................................................ 62
Interfaz de usuario ............................................................................................................. 70
5.4.1.
Interfaz gráfica para análisis de fallas y confiabilidad .............................................. 71
5.4.2.
Interfaz para el análisis del potencial eólico.............................................................. 77
Resultados y Análisis ................................................................................................................ 81
6.1.
Pruebas de cálculo de parámetros ..................................................................................... 81
6.2.
Aplicaciones prácticas ....................................................................................................... 82
6.2.1.
Análisis de fallas y confiabilidad .............................................................................. 83
6.2.2.
Análisis de velocidades de viento y potencial eólico ................................................ 94
Conclusiones ........................................................................................................................... 112
Bibliografía...................................................................................................................................... 114
Anexo 1 ........................................................................................................................................... 118
Anexo 2 ........................................................................................................................................... 119
Anexo 3 ........................................................................................................................................... 120
Anexo 4 ........................................................................................................................................... 121
Anexo 5 ........................................................................................................................................... 141
VII
Índice de Figuras
Figura N°1. Curva de la Bañera. ....................................................................................................... 10
Figura N°2. Diferentes curvas de Fallos. .......................................................................................... 11
Figura N°3. Curvas que componen la Curva de Bañera. ................................................................... 12
Figura N°4. Soluciones posibles según tipo de Fallos. ..................................................................... 13
Figura N°5. Representación de los estados TBF y TTR. .................................................................. 14
Figura N°6. Valores de
para distintos tipos de aerogeneradores...................................................19
Figura N°7. Curva de potencia aerogenerador de 2000 kW................................................................20
Figura N°8. Función densidad de probabilidad ................................................................................. 23
Figura N°9. Función de distribución acumulada ............................................................................... 25
Figura N°10. Funciones de densidad y distribución de la distribución Normal. .............................. 29
Figura N°11. Función de riesgo de la distribución Normal............................................................... 30
Figura N°12. Funciones de densidad y distribucion de la distribucion Log-Normal. ...................... 32
Figura N°13. Función de riesgo de la distribución Log-Normal. ...................................................... 33
Figura N°14. Función de densidad y distribución para distintos valores de . ................................. 34
Figura N°15 Distribución de Rayleigh para distintos valores de σ. .................................................. 35
Figura N°16. Funciones de densidad y distribución Exponencial. .................................................... 37
Figura N°17. Función de riesgo de la distribución Exponencial. ...................................................... 38
Figura N°18. Distribución de Weibull para distintos valores de β. ................................................... 40
Figura N°19. Representación de la tasa de fallo para distintos valores de β. .................................... 41
Figura N°20. Diagrama de flujo del programa para el análisis de falla ............................................ 63
Figura N°21. Diagrama de flujo del programa para el análisis de velocidades del viento ................ 64
Figura N°22. Diagrama de flujo tipo de datos a analizar .................................................................. 65
Figura N°23. Diagrama de flujo de la carga de datos........................................................................ 65
Figura N°24. Diagrama de flujo Nivel de Significancia ................................................................... 66
Figura N°25. Diagrama de flujo Calcular parámetros ....................................................................... 66
Figura N°26. Diagrama de flujo Pruebas bondad de ajuste............................................................... 67
Figura N°27. Diagrama de flujo del cálculos posteriores análisis de fallas ...................................... 68
Figura N°28. Diagrama de flujo del Graficas análisis de fallas ........................................................ 68
Figura N°29. Diagrama de flujo del Cálculos análisis de viento ...................................................... 69
Figura N°30. Diagrama de flujo del Cálculo Potencia Aerogenerador ............................................. 69
Figura N°31. Diagrama de flujo del Gráficas análisis de viento ....................................................... 70
Figura N°32. Interfaz gráfica para el análisis de fallas y tiempos de vida ........................................ 71
VIII
Figura N°33. Menú desplegable para el tipo de base de datos .......................................................... 72
Figura N°34. Botón “Abrir” .............................................................................................................. 72
Figura N°35. Sección Parámetros ..................................................................................................... 72
Figura N°36. Menú desplegable “Nivel de sensibilidad” .................................................................. 73
Figura N°37. Botón “Calcular Parámetros” ...................................................................................... 73
Figura N°38. Información mostrada al calcular parámetros ............................................................. 74
Figura N°39. Gráfica función de densidad de probabilidad calculada .............................................. 74
Figura N°40. Recuadro “Cálculos” Interfaz analisis de fallas .......................................................... 75
Figura N°41. Menú desplegable “Gráficas” ...................................................................................... 76
Figura N°42. Interfaz gráfica para el análisis de viento y potencial eólico ....................................... 77
Figura N°43. Recuadro “Cálculos” Interfaz análisis vientos ............................................................ 78
Figura N°44. Recuadro “Cálculo Potencia Aerogenerador” ............................................................. 79
Figura N°45. Recuadro “Gráficas” análisis de vientos ..................................................................... 80
Figura N°46. Parámetros tiempos entre fallas ejemplo 1 .................................................................. 83
Figura N°47. Parámetros tiempos de reparación ejemplo 1 .............................................................. 84
Figura N°48. Cálculo de confiabilidad usando la interfaz de usuario ............................................... 85
Figura N°49. Cálculo de confiabilidad usando la interfaz de usuario ............................................... 86
Figura N°50. Cálculo de confiabilidad usando la interfaz de usuario ............................................... 86
Figura N°51. Cálculo de confiabilidad usando la interfaz de usuario ............................................... 87
Figura N°52. Parámetros calculados sin considerar modos de fallas ................................................ 88
Figura N°53. Confiabilidad para esfuerzo de 500 mg. ...................................................................... 89
Figura N°54. Probabilidad de falla para esfuerzo de 500 mg. ........................................................... 89
Figura N°55. Parámetros calculados para modo de falla “A”. .......................................................... 90
Figura N°56. Confiabilidad para esfuerzo de 500 mg con modo de falla “A”. ................................. 91
Figura N°57. Probabilidad de falla para esfuerzo de 500 mg con modo de falla “A”. ..................... 91
Figura N°58. Parámetros calculados para el modo de falla “S”. ....................................................... 92
Figura N°59. Confiabilidad para esfuerzo de 500 mg con modo de falla “S”. ................................. 93
Figura N°60. Probabilidad de falla para esfuerzo de 500 mg con modo de falla “S”. ...................... 93
Figura N°61. Resultados análisis de velocidades del viento para el mes de Enero ........................... 95
Figura N°62. Resultados análisis de velocidades del viento para el mes de Febrero ........................ 96
Figura N°63. Resultados análisis de velocidades del viento para el mes de Marzo .......................... 97
Figura N°64. Resultados análisis de velocidades del viento para el mes de Abril ............................ 98
Figura N°65. Resultados análisis de velocidades del viento para el mes de Mayo ........................... 99
Figura N°66. Resultados análisis de velocidades del viento para el mes de Junio.......................... 100
IX
Figura N°67. Resultados análisis de velocidades del viento para el mes de Julio .......................... 101
Figura N°68. Resultados análisis de velocidades del viento para el mes de Agosto ....................... 102
Figura N°69. Resultados análisis de velocidades del viento para el mes de Septiembre ................ 103
Figura N°70. Resultados análisis de velocidades del viento para el mes de Octubre ..................... 104
Figura N°71. Resultados análisis de velocidades del viento para el mes de Noviembre ................ 105
Figura N°72. Resultados análisis de velocidades del viento para el mes de Diciembre ................. 106
Figura N°73. Resultados análisis de velocidades del viento para el año 2006 ................................ 108
X
Índice de Cuadros
Cuadro N°1. Estimadores de máxima verosimilitud ......................................................................... 46
Cuadro N°2. Números aleatorios entre 0 y 1.................................................................................... 52
Cuadro N°3. Datos seleccionados para aplicar Kolmogorov-Smirnov ............................................. 53
Cuadro N°4. Datos organizados de menor a mayor para prueba KS ................................................ 53
Cuadro N°5. Valores de
...................................................................................................... 54
Cuadro N°6. Organización para todos los valores ............................................................................ 61
Cuadro N°7. Organización de datos para pruebas de bondad ........................................................... 62
Cuadro N°8. Comparación de parámetros calculados ....................................................................... 81
Cuadro N°9. Tiempos de falla y tiempos de reparación ejemplo 1 ................................................... 83
Cuadro N°10. Esfuerzos y modos de falla ejemplo 2 ........................................................................ 87
Cuadro N°11. Resumen anual de la información obtenida. ............................................................ 107
Cuadro N°12. Comparación cálculo energías generadas ................................................................ 110
1
Resumen
La ley de distribución de Weibull es una de las más utilizadas en aplicaciones
industriales y biomédicas, ya que es capaz de representar una gran variedad de datos
reales, entre ellos la representación de confiabilidad de un componente, la vida útil de
un artículo, planta o animal, distribución de la velocidad del viento, etc.
Este trabajo tiene por objeto el desarrollo de un software, el cual basado en
registros históricos permita calcular los parámetros
de la distribución de Weibull,
para su aplicación en el análisis de fallas mecánicas, además tomando como base este
modelo también se desarrolló una aplicación para la caracterización del potencial
eólico.
Para lograr lo anteriormente mencionado se realizó la revisión bibliográfica de
los distintos conceptos básicos necesarios para el trabajar con la distribución de
Weibull, la estadística relacionada con el mantenimiento y con el análisis del recurso
eólico. Se analizaron dos distintos métodos para la estimación de parámetros de
Weibull, el método de Máxima Verosimilitud y el método de Mínimos Cuadrados.
Posteriormente se estudiaron las pruebas de bondad de ajuste KolmogorovSmirnov y Chi Cuadrado o X2, las cuales son aplicadas a las bases de datos para
verificar efectivamente que estos puedan ser modelados a través de una distribución de
Weibull.
El código de programación se realizó mediante el lenguaje del software
MATLAB y la interfaz gráfica con la herramienta GUIDE, el cual es el editor de
interfaz gráfica de usuario de MATLAB.
Finalmente se realizaron una serie de aplicaciones prácticas para verificar el
correcto funcionamiento del programa y demostrar su funcionalidad y alcance,
obteniéndose un programa que es capaz de calcular los parámetros de la distribución de
Weibull con una precisión a la altura de algunos software comerciales, con una interfaz
de usuario sencilla y sin la necesidad de conocer el lenguaje de programación para su
aplicación.
2
Summary
The Weibull distribution law is one of the most used in industrials and
biomedical applications, which is capable of representing a variety of real data,
including representation of a component reliability, the useful life of an item, plant or
animal, distribution of the wind speed, etc.
This paper aims to develop a software that based on historical records allows the
calculation of
parameters of the Weibull distribution, for application to the
analysis of mechanical failures, in addition based on this model an application for the
characterization of the wind potential is also developed.
To achieve the above, the literature review of the various basic concepts
necessary to work with the Weibull distribution was performed, the statistics related to
the maintenance and analysis of the wind resource. Two different methods for
estimating Weibull parameters were analyzed, the maximum likelihood method and
least squares method.
Later goodness of fit test Kolmogorov-Smirnov and Chi Square or
were
studied, which are applied to the database to verify that they can be effectively modeled
by a Weibull distribution.
The programming code was performed using the language of MATLAB
software and graphical interface with tool GUIDE, which is the graphical user interface
editor of MATLAB.
Finally a number of practical applications were performed to verify the correct
operation of the program and demonstrate its functionality and scope, yielding a
program that is able to calculate the parameters of the Weibull distribution with
accuracy up to some commercial software, with a simple user interface without the need
to know the programming language for its use.
3
Introducción
La calidad de los productos y sistemas es un concepto muy amplio que incluye:
confiabilidad, desempeño inicial, durabilidad, fácil de usar, reputación, seguridad,
compatibilidad con diferentes ambientes. De todos estos aspectos, la confiabilidad es la
característica más importante de un producto, expresado por la probabilidad de que
realizara sus funciones, bajo determinadas condiciones, durante un periodo específico
de tiempo. Se debe hacer la distinción entre la confiabilidad actual de un sistema, la
cual solo puede ser calculada durante el uso del producto y la confiabilidad predicha, la
cual se calcula utilizando datos de laboratorio.
El significado de la confiabilidad en la “vida” de una máquina, se puede
comparar con el significado de la salud en la vida de una persona. La utilidad o la
“calidad de vida” de una persona la determinan muchas propiedades: inteligencia,
rasgos de carácter, dedicación al trabajo, su aspecto físico, etc. Sin embargo, la salud es
la propiedad más importante de todas, porque de la misma, depende la manifestación de
sus otras cualidades. La persona saludable se enferma menos y puede realizar más
trabajo, también se necesitan menores gastos materiales, financieros y de tiempo para su
descanso y recuperación. [5]
En este sentido la confiabilidad de la maquina es su “salud” y las fallas
mecanicas o la pérdida de capacidad de trabajo son sus “enfermedades”. La máquina
que posee mayor confiabilidad tiene menor probabilidad de presentar fallas mecánicas,
por consiguiente tendrá menor probabilidad perder total o parcialmente su capacidad de
trabajo o producción. La medida cuantitativa de la confiabilidad es la tasa de fallo, tasa
a la cual se espera que un componente falle bajo condiciones conocidas.
La distribución Weibull es quizás el modelo de tiempos de vida más usado en
aplicaciones industriales y biomédicas.
La distribución Weibull comienza a ser
referenciada después de que el físico sueco, Waloddi Weibull (1887-1979) la usara en el
año de 1939 para representar la distribución del esfuerzo de rotura de materiales,
especialmente para el análisis de falla en elementos metalúrgicos, con todo el método
4
no atrajo mucha atención. Sin embargo, en 1951 en su artículo “A statistical
Distribution Function of Wide Applicability” en donde contempla varias de las
aplicaciones de este modelo, la concordancia que Weibull demostró entre sus datos
observados y aquellos que predijeron con los modelos Weibull era bastante
impresionante. Él usó la distribución para modelar datos de problemas que tratan con el
límite aparente de elasticidad del acero, la fuerza de la fibra de algodón de la india, la
vida de fatiga de un acero, la estatura de niños nacidos en las Islas Británicas y anchura
de frijoles de Phaseolus vulgaris. [22] [24]
La prevención de pérdidas o seguridad industrial aplicada con rigor científico
está basada, en gran parte, en la aplicación de los métodos probabilísticos a los
problemas de fallos en los procesos industriales. Todo ello se ha llevado a cabo a través
de una disciplina denominada ingeniería de confiabilidad, para la cual se disponen de
las adecuadas técnicas de predicción, que han sido fundamentales para el aseguramiento
de la calidad de productos y procesos. [6]
La distribución de Weibull complementa a la distribución Exponencial, a la de
Rayleigh y a la Normal, que son casos particulares de aquella. A causa de su mayor
complejidad sólo se usa cuando se sabe de antemano que es la que mejor describe la
distribución de fallos y los tiempos correspondientes no se ajustan a una distribución
más simple. En general es de gran aplicación en el campo de la mecánica.
En el campo de la energía eólica mediante métodos estadísticos, se analizan las
series temporales de viento. Se evalúan parámetros tales como la velocidad media a las
diferentes alturas de medición (con las que se extrapolará mediante modelos teóricos la
velocidad de viento a la altura de los aerogeneradores proyectados), distribuciones de
frecuencias de direcciones (también denominadas “rosas de los vientos”, que
representan el porcentaje de tiempo en que el viento proviene de una determinada
dirección) y distribuciones de frecuencias de las velocidades, así como sus
aproximaciones analíticas, principalmente distribución de Weibull, debido a la
5
significativa similitud entre ésta y las distribuciones de viento reales, que se obtienen a
partir de las series temporales de datos medidos de velocidad de viento.
La distribución de Weibull nos permite estudiar cuál es la distribución de fallos
de un componente clave de seguridad que pretendemos controlar, y que a través de
nuestro registro de fallos observamos que éstos varían a lo largo del tiempo, dentro de
lo que se considera tiempo normal de uso. Así como nos permite el estudio fallos
también nos permite estudiar el comportamiento de las velocidades del viento en un
emplazamiento específico, lo cual nos da la capacidad de caracterizar el potencial eólico
de dicho emplazamiento dada la relación existente entre velocidad del viento y potencia
contenida en este. Esta metodología es útil para aquellas empresas que desarrollan
programas de mantenimiento preventivo de sus instalaciones y para estudios de
factibilidad de proyectos eólicos.[23]
Los modelos y diseños en entornos programados que nos permiten hallar la
confiabilidad de equipos y sistemas, se convierten en valiosas herramientas de fácil
acceso y operación, obteniendo en los casos en estudio la respuesta deseada, sin
intervenir en complejos montajes que lleven a disfuncionalidades y restricciones de
tiempo.
Los costos de software en confiabilidad, en ocasiones se convierten en un sueño
inalcanzable para las pequeñas y medianas empresas, sin importar sus servicios y
productos a entregar, lo que aumenta de manera significativa el costo en reparaciones
ineficaces y por lo tanto ausentes de total viabilidad. Convirtiéndose en gastos, no en
inversiones que permitieran el crecimiento de las compañías.
El presente trabajo tiene como fin el diseño de un software que permita la
realización de los análisis de fallas, confiabilidad, y potencial eólico indicados
anteriormente
Este programa, se presenta como una ayuda en diferentes campos ya que
facilita el proceso de análisis de diversidad industrias interesadas en efectuar un
6
mantenimiento adecuado a sus equipos, suprimiendo factores externos que influencian
dicho proceso, eliminando a su paso variables como la experiencia o el juicio de quien
ejecuta el mantenimiento y concentrándose netamente en sus datos históricos, sus fallas,
su operatividad y su confiabilidad. Del mismo modo, permite caracterizar el potencial
eólico de un emplazamiento específico para estudios de factibilidad de proyectos
eólicos. Puede también utilizarse con fines académicos y explicativos, mostrando así el
comportamiento de los equipos e ilustrando las diferentes leyes de falla, así como el
significado de las mismas y algunas aplicaciones en la vida cotidiana. A su vez, la
programa, evalúa los datos a estudiar y mediante pruebas de bondad de ajuste se
determina si estos siguen una distribución de Weibull. El software se encarga
automáticamente de calcular los parámetros en función de los datos cargados.
7
Objetivo General
Desarrollar un software para el análisis de fallas y caracterización potencial
eólico de un emplazamiento, basado en registros históricos, mediante el cálculo de
parámetros de la distribución de Weibull.
Objetivos Específicos
Determinar los parámetros de escala y forma que representen la función
densidad de probabilidad para una distribución Weibull, tomando como base
registros históricos, tanto de fallas como de velocidades de viento.
Determinar mediante pruebas de Bondad de Ajuste, que los datos registrados
pueden ser modelados mediante la distribución de Weibull con los parámetros
obtenidos.
Permitir cálculos posteriores relacionados con el tipo de análisis realizado.
Desarrollar interfaces gráficas independientes, tanto para el análisis de fallas
mecánicas en máquinas como para el análisis de vientos,
que permitan la
adecuada interacción entre el usuario y el software diseñado.
Demostrar mediante aplicaciones prácticas la funcionalidad y alcance del
software desarrollado.
8
Metodología
Recopilación de material bibliográfico relacionado con la estadística
aplicada al mantenimiento y a la energía eólica.
Clasificación del material recopilado
Estudio del tratamiento de datos mediante métodos estadísticos.
Estudio y comprensión de los conceptos y principios relacionados con
variables aleatorias continuas y las distribuciones probabilísticas que las
modelan.
Estudio de la distribución de Weibull y distribuciones relacionadas.
Estudio comprensión de métodos de estimación de parámetros.
Estudio y comprensión de las pruebas de bondad de ajuste aplicadas a las
distribuciones aleatorias contínuas.
Investigación de programas comerciales para el cálculo de parámetros y
ajustes de datos mediante la distribución de Weibull.
Estudio de manuales y cursos acerca del entorno de programación y la
herramienta de diseño de interfaces de usuario del software MATLA para su
comprensión y aplicación en este proyecto.
Diseño esquemático del proceso de trabajo del software a desarrollar.
Escritura del código de programación del software a desarrollar en el
entorno de programación de MATLAB.
Diseño de la interfaz gráfica de usuario del software.
Desarrollo de pruebas para comprobar el funcionamiento y precisión del
cálculo de parámetros del software diseñado.
Ejecución del software alcanzado y su aplicación en casos reales.
9
1. Conceptos y principios básicos del mantenimiento
1.1.
Evolución histórica sobre el desarrollo de fallos
En este apartado veremos cómo ha ido evolucionando el desarrollo de fallos a lo
largo de la historia del mantenimiento. Partiendo de la conocida “Curva de la Bañera”
válida para equipos relativamente simples en los que la aparición de fallos se debía
principalmente a desgastes.
Con el avance de la tecnología cada vez los equipos son más complejos y poseen
más componentes eléctricos - electrónicos. Dichos equipos no se ajusten a la teoría de la
curva de la bañera.
Muchos estudios, sobre todo del sector de la aviación han demostrado que
existen al menos seis curvas con diferente modo de aparición de los fallos y sólo un
porcentaje muy pequeños de ellos se ajustan fielmente a la curva de la bañera. [8]
1.1.1. Curva de Bañera o de Davies
La curva de la bañera es un gráfica que representa los fallos durante el período
de vida útil de un sistema o máquina. Se llama así porque tiene la forma una bañera
cortada a lo largo.
10
Figura N°1. Curva de la Bañera.
En ella se pueden apreciar tres etapas:
Mortalidad Infantil o Fallos infantiles: esta etapa se caracteriza por tener una
elevada tasa de fallos que desciende rápidamente con el tiempo. Estos fallos
pueden deberse a diferentes razones como equipos defectuosos, instalaciones
incorrectas, errores de diseño del equipo, desconocimiento del equipo por parte
de los operarios o desconocimiento del procedimiento adecuado.
Fallos normales: etapa con una tasa de errores menor y constante. Los fallos no
se producen debido a causas inherentes al equipo, sino por causas aleatorias
externas. Estas causas pueden ser accidentes fortuitos, mala operación,
condiciones inadecuadas u otros.
Fallos por desgastes: etapa caracterizada por una tasa de errores rápidamente
creciente. Los fallos se producen por desgaste natural del equipo debido al
transcurso del tiempo.
11
1.1.2. Curvas de Fallos actuales
Muchos de los planes de mantenimiento se han basado en la curva de la bañera
clásica para definir los mismo pero estudios más actuales procedente del sector de la
aviación y militar han demostrado que los mecanismos de formación de fallos no tienen
por qué seguir las pautas de la curva de bañera.
A continuación se muestran en la Figura 2 las distintas curvas fallos a lo largo
del tiempo y el porcentaje de cada uno ellos según un estudio de la aviación [8]:
Figura N°2. Diferentes curvas de Fallos.
Curva A, La curva de bañera: Alta mortalidad infantil, seguida de un bajo nivel
de fallos aleatorios, terminado en una zona de desgaste. Sólo un 4% de los fallos
siguen esta curva. Coincide con equipos mecánicos históricos.
Curva B, El tradicional punto de vista: Pocos fallos aleatorios, terminando en
una zona de desgaste. Sólo un 2% de los fallos siguen esta curva. Coincide con
12
Equipos o Sistemas sometidos a fatiga y no diseñados para “vida infinita” como
por ejemplo sistemas electrónicos discretos.
Curva C, Un constante incremento en la probabilidad de fallo. Sólo un 5% de los
fallos siguen esta curva. Coincide con equipos o sistemas sometidos a corrosión.
Curva D, Un rápido incremento en la probabilidad de fallo, seguido de un
comportamiento aleatorio. Sólo un 7% de los fallos siguen esta curva. Coincide
con equipos electrónicos digitales.
Curva E Fallos aleatorios: No hay relación entre la edad funcional de los
equipos y la probabilidad de que fallen. Sólo un 14% de los fallos siguen esta
curva. Coincide con fallos en rodamientos bien diseñados.
Curva F Alta mortalidad infantil, seguida de un comportamiento aleatorio de la
probabilidad de fallos. El 68% de los fallos siguen esta curva. Coincide con
fallos en equipos o sistemas hidráulicos y neumáticos de diseño actual.
Por último se muestra en la Figura N°3 la curva de la bañera formada por las tres
curvas que la componen y a continuación de ésta en la Figura N°4 aparece en una
matriz las posibles soluciones en función del tipo de falla mecánica producida.
13
Figura N°3. Curvas que componen la Curva de Bañera.
Figura N°4. Soluciones posibles según tipo de Fallos.
1.2.
Confiabilidad
La confiabilidad R(t) se define como la probabilidad de que un bien funcione
adecuadamente durante un período determinado bajo condiciones operativas específicas
(por ejemplo, condiciones de presión, temperatura, velocidad, tensión o forma de una
onda eléctrica, nivel de vibraciones, etc.).
14
La confiabilidad se suele representar con la letra R (de la palabra inglesa
Reliability), una medida de la confiabilidad es el Tiempo Medio Entre Fallas (MTBF
por sus siglas en inglés).
1.1
En la práctica, la confiabilidad se mide como el tiempo medio entre ciclos de
mantenimiento o el tiempo medio entre dos fallos consecutivos MTBF. Se puede medir
en general por horas, kilómetros, horas de vuelo, piezas producidas, etc.
En la Figura N°5 se aprecia los distintos Tiempos Entre Fallas (TBF por sus
siglas en inglés) que hacen referencia al tiempo de funcionamiento de un activo y los
Tiempos Para Reparar (TTR por sus siglas en ingles) que se refieren a los tiempos de
paradas por reparación.
Figura N°5. Representación de los estados TBF y TTR.
R(t) es la Función de Confiabilidad, o dicho de otro modo, la probabilidad de
que un componente nuevo sobreviva más de un tiempo determinado, donde T se define
como la vida del bien o componente y t como el tiempo determinado para el cual se
quiere conocer dicha probabilidad.
1.2
La expresión
representa la probabilidad de que la el tiempo de vida
(T) de un componente o máquina sea mayor a un tiempo determinado (t), es decir la
15
probabilidad de no ocurrencia de una falla mecánica para un tiempo determinado.
F(t) es la Función de Distribución Acumulada siendo la probabilidad de que un
componente nuevo no sobreviva menos del tiempo t.
1.3
En este caso la expresión
representa la probabilidad de que el tiempo
de vida (T) de un componente o máquina sea menor a un tiempo determinado (t), o sea
probabilidad de ocurrencia de una falla mecánica para un tiempo determinado..
Derivando esta última obtenemos la Función de Densidad de Probabilidad f(t).
Ésta nos da una idea de la dispersión de la vida del componente. Esta función de vera en
detalle en el capítulo 3.
1.4
Dividiendo la ecuación 1.4 entre la ecuación 1.2 obtenemos la Tasa de Fallos
λ(t).
1.5
λ(t) es una característica de confiabilidad del componente. No tiene
interpretación física directa. Es bastante común que el comportamiento de fallos de un
componente sea descrito en términos de su tasa de fallos. Esta función al igual que la
expresión 1.4 se verá con más detalle en el capítulo 3.
1.3.
Mantenibilidad
Se define mantenibilidad M(t) como la probabilidad de que un equipo, después
de un falla o avería sea reparado y puesto en estado de funcionamiento en un tiempo
determinado. Una medida de la mantenibilidad es el MTTR (Mean Time To Repair) o
16
como se conoce en español “Tiempo Medio de Reparación”. En la Figura N°5 aparece
su ecuación y la representación de los distintos TTR (Time To Repair) o “Tiempo de
Reparación” en español, que componen el MTTR.
La definición anterior de mantenibilidad corresponde una definición desde un
punto de vista estadístico y cuantitativo, pero también puede ser definida
cualitativamente como la propiedad o característica de un sistema que representa la
cantidad de esfuerzo requerida para conservar su funcionamiento normal o para
restituirlo una vez se ha presentado una falla. Se dirá que un sistema es “Altamente
mantenible” cuando el esfuerzo asociado a la restitución sea bajo. Sistemas poco
mantenibles o de “Baja mantenibilidad” requieren de grandes esfuerzos para sostenerse
o restituirse.
Su Tasa de Reparación es µ(t)
1.6
1.4.
Disponibilidad
Se define la disponibilidad D(t) como la probabilidad en el tiempo de asegurar
un servicio requerido.
Otra definición común en mantenimiento para la disponibilidad es: el porcentaje
de equipos o sistemas útiles en un determinado momento, frente al parque total de
equipos o sistemas.
La ecuación de la disponibilidad está en función de la confiabilidad y de la
mantenibilidad, siendo esta:
1.7
17
2. Caracterización del potencial eólico
A la hora de analizar la rentabilidad de un proyecto eólico resulta imprescindible
evaluar cuidadosamente mediante herramientas estadísticas todos aquellos parámetros
representativos de su potencial.
Las ciencias de la atmósfera, ya sea en las diferentes especialidades relacionadas
con la meteorología o con la climatología, hacen un amplio uso de diferentes métodos
estadísticos. Así, la comprensión de un fenómeno fundamentalmente atmosférico, como
es el potencial de un emplazamiento donde se proyecta un parque eólico, provendrá en
buena parte del análisis estadístico de datos.
Para la evaluación del recurso eólico durante la fase de prospección en un
emplazamiento específico, se realizan mediciones de viento mediante la instalación de
torres anemométricas en varios puntos del proyecto. De igual forma, también se
recopilan registros históricos provenientes de estaciones meteorológicas con un número
significativo de años de medidas. Estas mediciones de viento consisten en series
temporales de datos de velocidad y dirección de viento, generalmente con promediados
diezminutales, así como otros parámetros tales como la desviación estándar de la
velocidad, presión atmosférica y temperatura. [23]
Como se ha indicado anteriormente, la expresión analítica más usada en estudios
de recurso eólico para representar la probabilidad de velocidades de viento es la
distribución Weibull que, en función de los dos parámetros que la definen, permite la
evaluación de varias propiedades importantes de las características del viento, como por
ejemplo la probabilidad de que existan velocidades de viento superiores a una
determinada, la probabilidad de que existan velocidades de viento entre dos límites de
interés, la velocidad media, así como una estimación de la energía producible en el
punto de interés, al comparar su distribución Weibull asociada con la curva de potencia
del aerogenerador estudiado. [26]
18
2.1.
Potencia contenida en el viento y potencia aprovechable
Los generadores eólicos extraen energía contenida en el viento para convertirla
en energía eléctrica y entregarla a la red. Esta energía que se busca extraer del viento es
fundamentalmente energía cinética y se relaciona con el cubo de la velocidad del viento
a través de la siguiente expresión [3];
2.1
Donde:
es la potencia contenida en el viento en W
es la densidad del aire a nivel del mar a 15°C
es el área barrida por las palas del aerogenerador de longitud R en m2
es la velocidad del viento en m/s
Dada la variabilidad de la velocidad, la caracterización del potencial eólico
disponible de un lugar se debe realizar a partir de la determinación de los valores de la
potencia correspondientes a cada velocidad y promediar estos para un determinado
periodo de tiempo, por ejemplo un año. De esta forma, se define el potencial eólico
disponible en un punto como la potencia media eólica por unidad de superficie o en
otras palabras por la densidad de potencia (fórmula 2.2), para un determinado periodo
de tiempo, generalmente un año, supuesta la densidad del aire constante.
∫
Donde:
es la potencia disponible en el viento en W
es el área barrida por las palas del aerogenerador de longitud R en m2
es la densidad del aire a nivel del mar a 15°C
la velocidad del viento en m/s
2.2
19
es la función de densidad de probabilidad de Weibull en función de la velocidad
del viento
Sin embargo, de acuerdo con el principio de la conservación de la energía, solo
es posible extraer una parte de esta. El límite de Betz establece en 0.59 la proporción
máxima de energía que podemos extraer del viento utilizando un aerogenerador. [3],
[23]
El coeficiente de potencia (
), se puede entender como el rendimiento del
aerogenerador, siendo, el porcentaje de energía contenida en el viento que atraviesa el
rotor y que es transformada en energía mecánica en el eje del rotor. Depende de la pala
y del sistema de control de la máquina.
La potencia se ve entonces afectada por el coeficiente
, donde
a mayor eficiencia aerodinámica del sistema generador, mas alto será el valor de
En aplicaciones reales, el valor de
.
, rara vez toma valores superiores a 0.5 [3],
siendo más comunes valores entre 0.4 y 0.45 para aerogeneradores modernos como se
puede ver en la Figura N°6 [28].
Figura N°6. Valores de
para distintos tipos de aerogeneradores
20
En los generadores de velocidad variable, es posible modificar los parámetros de
operación logrando mantener el valor de
lo más alto posible y aproximadamente
constante en la zona de operación por debajo de la potencia nominal.[3]
2.2.
Curva de potencia de los aerogeneradores
Para poder estimar la energía obtenida por un aerogenerador debemos disponer
de la distribución de velocidad del viento del sitio y contar con la curva de potencia del
aerogenerador entregada por el fabricante.
Dicha curva de potencia indica cual será la potencia generada por el
aerogenerador para las distintas velocidades del viento. La curva de potencia se obtiene
empíricamente y es entregada por el fabricante del aerogenerador.
Figura N°7. Curva de potencia aerogenerador de 2000 kW
21
Por otro lado debemos tener en cuenta que el aerogenerador requiere una
velocidad de viento mínima para poder operar (velocidad de cut-in), que oscila
alrededor de 3-5 m/s. Además, si la velocidad del viento es muy elevada, puede reducir
la vida útil del generador, razón por la cual existe un valor de velocidad máxima
(velocidad de cut-out) por encima del cual el aerogenerador no opera. Esta velocidad se
encuentra alrededor de los 25 m/s.[26]
2.3.
Cálculo de potencia generada
Teniendo en cuenta lo expuesto anteriormente, podemos obtener la potencia
media generada por el aerogenerador de la siguiente manera [23]:
∫
2.3
Donde:
es la potencia generada por el aerogenerador en kW o en las unidades en que se
encuentre la curva de potencia.
es la velocidad mínima a la que el aerogenerador comienza operar.
es la velocidad máxima a la cual el aerogenerador deja de operar.
es la función que describe la curva de potencia del aerogenerador .
es la función densidad de probabilidad de Weibull en función de la velocidad del
viento.
22
3. Variables aleatorias continuas
3.1.
Variable aleatoria
Una variable aleatoria es una variable cuyos valores se obtienen
de
experimentos o eventos donde la medición o el valor de dicha variable se encuentran en
un conjunto de posibles valores ya que abarca un intervalo de números haciendo que,
la cantidad de valores que pueda tomar la variable sea incontablemente infinito.
Una variable aleatoria
es una función real definida en el espacio muestral
asociado a un experimento aleatorio, Ω
En general, la mayoría
de los problemas en la ingeniería de
la confiabilidad se ocupan de medidas cuantitativas, tales como la tiempo a la falla de
un componente, o si el componente falla o no. En la sentencia de un componente para
ser defectuoso o no-defectuoso, solamente dos resultados son posibles. Podemos
entonces denotar una variable aleatoria X como representante de estos resultados
posibles, es decir defectuoso o no-defectuoso. En este caso, X es una variable aleatoria
que puede adquirir solamente estos valores.
En el caso del tiempo a la falla o tiempo de vida, nuestra variable aleatoria X
puede adquirir el tiempo a la falla (o el tiempo a un acontecimiento del interés) del
producto o componente y puede estar en una gama a partir de 0 al infinito (puesto que
no sabemos el tiempo exacto a priori).
En el primer caso, donde la variable aleatoria puede adquirir solamente dos
valores discretos (vamos a decir defectuoso X = 0 y no-defectuoso X=1), la variable se
dice ser una variable aleatoria discreta. En el segundo caso, nuestro producto se puede
encontrar fallando en cualquier momento después del tiempo 0, es decir en (12, 4 horas
o en 100, 12 horas) y así sucesivamente. En este caso, nuestra variable aleatoria X se
dice ser una variable aleatoria continua. Surge un tercer caso, cuando el producto puede
23
fallar en cualquier momento después del tiempo cero, pero por alguna razón sólo se
puede observar el experimento hasta el tiempo t0, generando, esta situación una variable
aleatoria que se denomina como variable aleatoria mixta.
En el presente trabajo se hará referencia a variables aleatorias continuas.
En general, asumiremos que el tiempo de vida es una variable continua, la cual
denotaremos por , y que toma valores en el intervalo
. Esta distribución viene
caracterizada por las funciones definidas a continuación.
3.2.
Función densidad de probabilidad
La función densidad de probabilidad es una función que describe la probabilidad
relativa de una variable aleatoria que se produzca en un momento dado, es decir,
caracteriza el comportamiento probable de una población. La probabilidad de una
variable aleatoria a caer dentro de una región particular está dada por la integral de la
densidad de esta variable en dicha región.
Figura N°8. Función densidad de probabilidad
24
Para una variable aleatoria continua x, una función densidad de probabilidad es
una función de tal manera que:
3.3.
Función de distribución acumulada
La función de distribución acumulada de la variable aleatoria continua ,
,
representa la probabilidad de que esta variable T sea menor o igual a un valor t dado.
Puede ser interpretada como la probabilidad de que ocurra una falla antes del tiempo t,
que el tiempo de falla sea menor o igual al tiempo t, o la probabilidad de que la
velocidad del viento sea menor o igual a cierta velocidad dada. Todo dependiendo de la
variable que se esté estudiando.
∫
Esta función es continua, monótona no decreciente y además verifica que
y
25
Figura N°9. Función de distribución acumulada
3.4.
Función de Confiabilidad o distribución acumulada complementaria
La función de distribución acumulada complementaria
, de la variable
aleatoria continua , representa la probabilidad de que la variable T sea mayor o igual a
un valor t dado. Puede ser interpretada como la probabilidad de que no ocurra una falla
antes del tiempo t (confiabilidad), que el tiempo de falla sea mayor o igual a un tiempo t
dado, o que la velocidad del viento se mayor o igual a cierta velocidad dada.
∫
Esta función es continua, monótona decreciente y además verifica que
y
26
3.5.
Función de riesgo
Un concepto muy importante a tener en cuenta cuando trabajamos con
distribuciones asociadas a tiempos de vida es la función de riesgo o tasa de fallo
,
que se define como la probabilidad instantánea de que un componente falle en el
instante . En términos de probabilidad se interpreta como el límite de la probabilidad
falle antes del tiempo
condicionada de que
sabiendo que no había fallado en el
instante . Esto no es más que el cociente entre la función de densidad
de confiabilidad
y la función
.
Entonces, la función de riesgo es
3.3
Definimos la función de riesgo acumulada,
, como
3.4
La función de riesgo acumulada y la función de distribución verifican la
siguiente relación
3.5
La función de riesgo es una característica muy importante de las distribuciones
asociadas a variables correspondientes a tiempos de vida.
27
Funciones de riesgo decrecientes surgen cuando al principio del funcionamiento
la probabilidad de falla mecánica es alta debido a posibles defectos de
fabricación.
Funciones de riesgo constantes tienden a aparecer en conjuntos donde las fallas
mecánicas son debidos a un fenómeno aleatorio como accidentes o shocks.
Funciones de riesgo crecientes aparecen cuando se produce un envejecimiento
del componente.
Estas tres formas de riesgo o fallas se combinan para generar la curva de bañera.
3.6.
Distribuciones de probabilidad continuas
Las distribuciones de probabilidad son funciones matemáticas teóricas que se
utilizan para realizar previsiones, que describen la forma en que se espera que varíen los
resultados de un experimento. Por lo tanto son útiles en mantenimiento, debido a que,
ayudan a tomar decisiones en condiciones de incertidumbre.
Las distribuciones de probabilidad continuas más difundidas son las siguientes:
Distribución Normal o de Gauss
Distribución Log-Normal
Distribución Gamma
Distribución Exponencial
Distribución Rayleigh
Distribución de Weibull
Las que se detallaran a continuación.
28
3.6.1. Distribución Normal
Es la distribución utilizada con más frecuencia en estadística, aunque no ocurre
así en estudios de confiabilidad debido a su carácter simétrico, ya que habitualmente los
tiempos de vida presentan un comportamiento asimétrico.
Se dice que una variable aleatoria continua T sigue una distribución normal de
parámetros µ y σ y se denota T ~ N (µ, σ) si su función de densidad está dada por:
3.6
t
µ es la media
σ es la desviación estándar
R
Sus funciones de distribución acumulada y confiabilidad son
3.7
3.8
respectivamente, para las cuales no existen expresiones analíticas explícitas, aunque sí
se pueden aproximar numéricamente.
29
La función de riesgo, dado que la función de distribución Normal no tiene forma
explícita, no puede ser calculada de manera directa mediante el cociente entre la función
de densidad y la función de confiabilidad, aunque sí se puede aproximar
numéricamente. Esta función está representada en la Figura N°10. Cuando
y
, esta distribución se denomina distribución Normal estándar, cuya función de
densidad, denotada por
es
3.9
Su función de distribución es
3.10
Figura N°10. Función de riesgo de la distribución Normal con μ=5 .
30
Figura N°11. Funciones de densidad (izquierda) y distribución (derecha) de la
distribución Normal con μ=5.
Algunas propiedades de la distribución normal son:
Es simétrica respecto de su media, µ.
La moda y la mediana son ambas iguales a la media, µ.
Los puntos de inflexión de la curva se dan para x = µ - σ y x = µ + σ
El intervalo [µ-σ,µ+σ] se encuentra comprendida, aproximadamente, el 68,26%
de la distribución
El intervalo [µ-2σ,µ+2σ] se encuentra comprendida, aproximadamente, el
95,44% de la distribución
El intervalo [µ-3σ,µ+3σ]
99,74% de la distribución
se encuentra comprendida, aproximadamente, el
31
3.6.2. Distribución Log-Normal
Este modelo de distribución se ha utilizado en multitud de aplicaciones
asociadas a ingeniería, medicina y otras áreas.
Una variable puede ser modelada como Log-Normal si puede ser considerada
como un producto multiplicativo de muchos pequeños factores independientes. Un
ejemplo típico es un retorno a largo plazo de una inversión: puede considerarse como un
producto de muchos retornos diarios.
Diremos que la variable aleatoria T sigue una distribución Log-Normal, y lo
denotaremos como
con media
aleatoria
, si la variable
sigue una distribución Normal
y desviación típica . Por lo tanto, si la función de densidad de la variable
es
3.11
Con
, entonces la función de densidad de
es
3.12
Con
, que es la densidad de la distribución Log-Normal. Su función de
distribución acumulada es
3.13
32
donde
es la función de distribución Normal estándar dada en la expresión 3.9.
Las funciones de densidad y distribución están representadas en la Figura N°12.
Figura N°12. Funciones de densidad (izquierda) y distribucion (derecha) de la
distribucion Log-Normal para
.
La función de confiabilidad es
(
La función de riesgo,
caracteriza por valer cero en
)
3.14
, que se corresponde con la Figura N°13, se
, y como podemos comprobar, para el caso
,
la función de riesgo crece hasta un máximo y luego decrece, acercándose a cero a
medida que tiende a
.
33
Figura N°13. Función de riesgo de la distribución Log-Normal para
3.6.3. Distribución de Gamma
Es una distribución adecuada para modelar el comportamiento de variables
aleatorias continuas con asimetría positiva. Es decir, variables que presentan una mayor
densidad de sucesos a la izquierda de la media que a la derecha. En su expresión se
encuentran dos parámetros, siempre positivos, y de los que depende su forma y alcance
por la derecha, y también la función Gamma
, responsable de la convergencia de la
distribución.
.
El primer parámetro sitúa la máxima intensidad de probabilidad y por este
motivo en algunas fuentes se denomina “la forma” de la distribución: cuando se toman
valores próximos a cero aparece entonces un dibujo muy similar al de la distribución
exponencial. Cuando se toman valores más grandes de α el centro de la distribución se
desplaza a la derecha y va apareciendo la forma de una campana de Gauss con asimetría
34
positiva. Es el segundo parámetro β el que determina la forma o alcance de esta
asimetría positiva desplazando la densidad de probabilidad en la cola de la derecha.
Para valores elevados de β la distribución acumula más densidad de probabilidad en el
extremo derecho de la cola, alargando mucho su dibujo y dispersando la probabilidad a
lo largo del plano. Al dispersar la probabilidad la altura máxima de densidad de
probabilidad se va reduciendo; de aquí que se le denomine “escala”. Valores más
pequeños de β conducen a una figura más simétrica y concentrada, con un pico de
densidad de probabilidad más elevado.
La función de densidad de la distribución Gamma es:
3.15
donde x > 0 y β, α son parámetros positivos. En la Figura N°14 se muestra la función de
densidad.
Figura N°14. Función de densidad y distribución para distintos valores de .
La función de distribución acumulada es,
35
]
∫
3.16
como se puede ver en la Figura N°14.
La esperanza matemática o media es,
3.17
3.6.4. Distribución Rayleigh
Es una función de distribución continua. Se suele presentar cuando un vector
bidimensional tiene sus dos componentes, ortogonales, independientes y siguen una
distribución normal. Su valor absoluto seguirá entonces una distribución de Rayleigh.
Figura N°15 Distribución de Rayleigh para distintos valores de σ.
La función densidad de probabilidad para la distribución Rayleigh está definida por la
siguiente expresión:
36
( )
( )
3.18
Donde:
α: Parámetro de escala
t: Variable aleatoria que mide el tiempo de fallas.
Por otro lado, la función distribución acumulada se obtiene de la integral de la
función densidad de probabilidad evaluada en un intervalo y se define como:
(
)
3.19
Su esperanza matemática media es:
√
3.20
3.6.5. Distribución Exponencial
Históricamente, este modelo de distribución fue muy utilizado en el trabajo con
tiempos de vida útil, debido a la simplicidad de los métodos estadísticos que
proporciona. La función de densidad de una variable aleatoria con distribución
Exponencial es
3.21
37
con
, siendo
el parámetro del modelo. Su función de distribución acumulada
es
3.22
y su función de confiabilidad es
3.23
Figura N°16. Funciones de densidad (izquierda) y distribución (derecha) Exponencial.
Su función de riesgo es constante y su valor es el parámetro del modelo, , es
decir
3.25
Emplearemos la notación
para indicar que
es una variable aleatoria
con función de densidad (1.1). La media y la varianza de esta distribución vienen dadas
por los valores
y
, respectivamente. El p-cuantil es
38
3.26
Cuando el parámetro
es igual a 1 la llamaremos distribución Exponencial
estándar, cuyas funciones de densidad y distribución se corresponden con la línea de
color rojo de la Figura N°17.
Figura N°17. Función de riesgo de la distribución Exponencial con.
La función de distribución que se utiliza más a menudo para modelar la
confiabilidad es la exponencial. El motivo es que:
Es sencilla de tratar algebraicamente
Se considera adecuada para modelar el intervalo de vida funcional del ciclo de
vida del dispositivo
La distribución exponencial aparece cuando la tasa de fallos es constante, λ(t)=λ
39
La tasa de fallos se considera constante, entonces la función de distribución de
los fallos es exponencial. De las propiedades de ésta se deduce que la probabilidad de
que una unidad que está trabajando falle en el próximo instante es independiente de
cuánto tiempo ha estado trabajando.
Esto implica que la unidad no presenta síntomas de envejecimiento, es
igualmente probable que falle en el instante siguiente cuando está nueva o cuando no lo
está.
3.6.6. Distribución de Weibull
La distribución de Weibull es una distribución continua y triparamétrica, es
decir, está completamente definida por tres parámetros y es la más empleada en el
campo de la Confiabilidad. Para efectos de este trabajo se empleara la distribución de
dos parámetros.
La distribución de Weibull es una distribución de probabilidad continua. La
función de densidad de una variable aleatoria:
3.27
Esta forma de expresar la función de densidad de la distribución Weibull es la
empleada por el mismo Waloddi Weibull, aunque cabe mencionar que en la actualidad
algunos autores emplean otras formas equivalentes tales como:
3.28
o bien
40
3.29
La primera expresión, se puede ver que es equivalente a la segunda sustituyendo
a beta en la primera por beta elevado a la alfa.
Para ver la equivalencia de la primera y la tercera expresión se efectúa la
siguiente reparametrización
en la primera expresión.
Por último para ver la equivalencia entre la segunda y tercera expresión se lleva
a cabo la siguiente reparametrización
⁄
en la segunda expresión.
Donde β > 0 es el parámetro de forma y η > 0 es el parámetro de escala o
característica de vida de la distribución.
En la Figura N°18 se ve como varía la función de distribución para distintos
valores de β.
Figura N°18. Distribución de Weibull para distintos valores de β.
41
Su función de distribución acumulada es:
( )
Para valores de x
3.30
0, siendo nula en x < 0.
Siendo su tasa de fallo:
( )
3.31
En la Figura N°19 se puede como varía la tasa de fallo para distintos valores de η y β.
Figura N°19. Representación de la tasa de fallo para distintos valores de β.
El parámetro de forma nos indica el tipo de fallo que es, así como el tipo de
distribución probabilística que podemos seguir.
42
Su función de Confiabilidad
( )
3.32
Su Esperanza matemática o media:
(
)
3.33
Donde Γ es la función Gamma.
Características de la distribución Weibull
La distribución de Weibull nos ayuda a conocer:
El tipo de mecanismos de fallo que ha sido el causante del mismo.
Cantidad de fallos que se pueden esperar en un futuro.
Confiabilidad de un equipo existente.
La función de riesgo adopta las siguientes formas en función del parámetro de
forma,
:
Tipo de fallos que se pueden dar:
0< β < 1 Mortalidad infantil. La función de riesgo es decreciente, es decir, la
tasa de fallo disminuye al aumentar el tiempo.
β = 1 La función de riesgo es constante, por lo que no depende del tiempo. En
este caso, la distribución Weibull coincide con la Exponencial.
o Fallos aleatorios independientes del tiempo.
o Errores humanos.
43
o Errores de Mantenimiento.
o Sistemas de varios componentes.
o Combinación de dos o tres modos de fallos diferentes.
1 < β < 4 Tasa creciente.
o Implica desgastes tempranos.
o Fatiga de baja frecuencia, con β = 2,5 hasta β = 4.
o Fallos en rodamientos de bolas β = 2.
o Fallos en rodamientos de rodillos β = 1,5.
o Corrosión o erosión con β = 3 hasta β = 4.
o Corrosión o esfuerzos con β = 5 o mayor.
o Fallos en correas β = 2,5.
4 < β Tasa creciente.
o Envejecimiento operacional.
o Corrosión por esfuerzos.
o Pérdida de propiedades de los materiales.
o Materiales frágiles como la cerámica.
o Algunos tipos de erosión.
Distribuciones que pueden ser aproximadas a través de la distribución de
Weibull:
β = 1 Distribución Exponencial.
β = 2 Distribución de Rayleigh.
3 ≤ β ≤ 4 Distribución Normal.
44
4. Métodos de estimación de parámetros
4.1.
Máxima verosimilitud
El método de máxima verosimilitud suele generar estimadores insesgados de la
mínima varianza, siendo este un procedimiento frecuente para ajustar un modelo y
encontrar sus parámetros característicos.
Cuando queremos estimar un parámetro de una población de la cual se conoce
la familia a la cual pertenece, es decir, su forma, por ejemplo se sabe que dicha
población se puede modelar con una distribución Normal, ó Poisson, o Binomial, etc,
pero no se conocen sus parámetros, podemos tomar una muestra aleatoria para con base
en ella, construir una estadística que nos permita estimar dicho parámetro.
Dada una muestra observada
y una ley de probabilidad
, la
verosimilitud cuantifica la probabilidad de que las observaciones provengan
efectivamente, de una muestra (teórica) de la ley
Sea C un conjunto finito o numerable, {
.
} una familia de leyes de probabilidad
sobre C y n un entero. Llamamos verosimilitud asociada a la familia {
ada
}, para una n-
de elementos de C y un valor θ del parámetro a la función definida por:
4.1
Estimar un parámetro por el método de máxima verosimilitud, es proponer como
valor del parámetro aquél que maximice la verosimilitud, es decir, a la probabilidad de
observar los datos como realización de una muestra de la ley
.
Para la mayoría de las leyes de probabilidad usuales, el estimador de máxima
verosimilitud se define de forma única y se calcula explícitamente. En el plano teórico
tiene muchas ventajas. Bajo hipótesis que cumplen numerosos modelos de uso
45
corriente, se demuestra que es asintóticamente insesgado y consistente. Se demuestra,
además, que su varianza es mínima, por lo tanto el método de máxima verosimilitud es
teóricamente el mejor de los métodos de estimación. Cuando una determinación
explícita es imposible, hay que recurrir a una determinación numérica, empleando un
algoritmo de optimización.
En la mayor parte de los casos de interés práctico, la ley
y por tanto también
la verosimilitud, tienen una expresión calculable en función de θ. Para calcular el
máximo de la verosimilitud, es necesario determinar los valores para los cuales la
derivada de la verosimilitud se anula, pero por definición la verosimilitud es un
producto de probabilidades o de densidades, lo cual puede ser bastante complicado de
derivar. Es preferible derivar una suma, y es por esto que comenzamos por sustituir la
verosimilitud por su logaritmo. Al ser el logaritmo una función creciente, es equivalente
maximizar
o
. Una vez determinado el valor de θ
para el cual la derivada se anula, hay que asegurarse con la ayuda de la segunda
derivada que el punto en cuestión es realmente un máximo. Es decir el punto en que la
verosimilitud es máxima, es la solución del sistema de k ecuaciones [2], [4].
46
Cuadro N°1. Estimadores de máxima verosimilitud
Encontrar las estimaciones para la distribución Weibull, consiste en tomar las
derivadas parciales de la función de probabilidad con respecto
a los parámetros,
organizar las ecuaciones que resultan igual a cero y resolver simultáneamente para
determinar los valores de los parámetros estimados. [10], [22].
. Cabe resaltar que la manera como se hallan los parámetros en el programa es
mediante el Toolboox de Matlab y su comando
, el cual
utiliza este mismo método.
4.2.
Mínimos Cuadrados
Este método es el utilizado tradicionalmente para la estimación de los parámetros
de la distribución de Weibull, su mayor dificultad radica en cálculo del rango de la
mediana, ya que por lo general se utiliza una aproximación de esta, en general este
método es relativamente sencillo en comparación con el de Máxima Verosimilitud, pero
tedioso por la gran cantidad de pasos para llegar a un resultado.
47
Cabe señalar que la precisión de este método depende de la cantidad de datos
registrados, a mayor cantidad mayor precisión. Siendo en general menos preciso que la
Máxima Verosimilitud. [5], [21].
El método de los mínimos cuadrados permite calcular los parámetros de forma y
escala, mediante la transformación doble logarítmica de la función de distribución
acumulativa.
Deducción de la ecuación lineal de regresión:
( )
Función acumulativa de Weibull.
( )
( )
[
[
]
[
( )
]
(
( )
Aplicando logaritmos naturales.
Propiedad exponencial de los logaritmos.
)]
( )
[
(
Aplicando logaritmos naturales.
)]
La expresión 4.2 representa una ecuación lineal de la forma
4.2
48
4.3
La cual es una recta de regresión, con:
[
(
)]
4.4
De la expresión 4.3 se concluye que el parámetro de forma, β, es la pendiente de
la recta de regresión.
De la expresión 4.4 se observa que el parámetro de escala , está en función del
intercepto b de la recta de regresión y del parámetro de escala; por lo tanto:
4.5
Rango de mediana
Para poder trazar la recta de regresión, se debe calcular un estimador para la
función de distribución acumulativa F(x). Este estimador, llamado Rango de mediana,
es un estimador no paramétrico basado en el orden de las fallas. Este aspecto implica
que la muestra de datos se debe organizar de menor a mayor (en forma ascendente).[19]
La expresión matemática para este estimador es:
4.6
49
Donde:
: Rango de mediana para un nivel de confianza (1-α), donde α es el nivel de
significancia y toma el valor de 0.5 para este estimador.
i: Orden de la falla.
n: Número total de datos de la muestra.
: Valor crítico de la distribución F de Snedecor, evaluada en el nivel de
significancia α y con grados de libertad
.
Generalmente el rango de mediana se aproxima mediante la siguiente expresión
4.7
Donde:
RM(xi): Rango de mediana.
i: Orden de falla.
n: Número total de datos de la muestra.
Hallando la pendiente β:
4.8
Hallando b:
4.9
50
4.3.
Pruebas de bondad de ajuste
Las pruebas de bondad de ajuste tienen por objetivo determinar si los datos se
ajustan a una determinada distribución. Es necesario resaltar, que las pruebas están en
capacidad de rechazar con certeza absoluta la hipótesis nula, pero si dicha hipótesis se
acepta quiere decir que la distribución escogida es posiblemente la que describe el
comportamiento de los datos.
4.3.1. Test de Kolmogorov-Smirnov
Es una prueba no paramétrica que se utiliza para determinar la bondad de ajuste.
Estos test se hacen necesarios cuando la distribución no puede ser definida
concretamente pues son los datos observados los que la construyen.
La prueba de Kolmogorov-Smirnov se basa en la diferencia entre la Función de
distribución acumulativa y la Función de distribución empírica. La discrepancia
obtenida entre la función de distribución teórica de la empírica da como resultado la
distancia de Kolmogorov-Smirnov y con esta se puede determinar si la hipótesis se
acepta o se rechaza. [6]
Claramente, la prueba de Kolmogorov-Smirnov se plantea de la siguiente manera [25]:
1. Se plantea la hipótesis nula:
Donde
es la función de distribución de una ley continua dada
2. Se define la función de distribución empírica
51
3. Se plantea la distancia de Kolmogorov-Smirnov, realizando restas por encima y
por debajo de la función entre la función de distribución acumulada y la función
de distribución empírica
4.10
Donde :
: Función de distribución acumulada
4. Finalmente, una vez obtenida la distancia de Kolmogorov-Smirnov se verifica
que dicha distancia sea menor o igual a la Distribución del estadístico de
Kolmogorov-Smirnov
4.11
Si y solo si esta condición se cumple, se puede decir que se cumple la hipótesis nula
.
La tabla de distribución del estadístico de Kolmogorov-Smirnov ó los límites de
aceptación para el test K-S se encuentra en el Anexo 1
52
Ejemplo
De una tabla de números aleatorios se eligen los siguientes 50 (divididos entre 100 para
que su valor oscile entre 0 y 1)
Cuadro N°2. Números aleatorios entre 0 y 1
Paso 1
Se desea probar la hipótesis
: Provienen de una distribución uniforme en
[0,1], a un nivel de significancia del 90%
Paso 2
Se selecciona una muestra de tamaño n de números seudoaleatorios
53
Cuadro N°3. Datos seleccionados para aplicar Kolmogorov-Smirnov
Paso 3
3.1. Se organiza la tabla anterior para que se cumpla la condición
para
toda posición .
Cuadro N°4. Datos organizados de menor a mayor para prueba KS
3.2. Si
, entonces
posición , siendo
. Se construye
.
para toda
54
Cuadro N°5. Valores de
Paso 4
Se evalúa:
Es decir, se busca la mayor de las desviaciones en valor absoluto, para lo
cual se deben calcular todas las desviaciones entre los valores de probabilidad
acumulada teórica y los valores de probabilidad acumulada empírica.
El valor D máximo ocurre para
, que esta en la posición
es decir con una probabilidad acumulada teórica de
,
.
Paso 5
Para un nivel de significancia del 90% y una muestra de 50 números se
tiene de la Tabla Kolmogorov – Smirnov (ver anexo 1), un valor de 0.172.
Como
se acepta
, o sea, los números si provienen
de una distribución uniforme en el intervalo cerrado [0,1].
55
4.3.2. Prueba Chi-Cuadrado
Es una prueba de bondad de ajuste también conocida como la prueba
de
Pearson o Chi-Cuadrado. La utilización de estos métodos se hace recomendable cuando
no se puede asumir que los datos se ajusten a una distribución conocida. Es considerada
como una prueba no paramétrica que mide la discrepancia o distancia entre una
distribución observada y otra teórica (bondad de ajuste).[2], [17]
La fórmula del estadístico es la siguiente:
4.12
Teniendo en cuenta que
Donde:
Frecuencia observada de la muestra
Frecuencia esperada según la distribución teórica
Tamaño de la muestra
Para calcular el valor de Chi-Cuadrado se realiza lo siguiente [17]:
1. Se divide la muestra de datos en intervalos y se obtienen la frecuencias
observada para cada intervalo (Una buena aproximación para la cantidad de
intervalos necesarios puede ser √
donde
es el tamaño de la muestra).
56
2. Se calcula la frecuencia esperada para cada intervalo, basados en la función
distribución de probabilidad acumulada.
3. Con la fórmula del estadístico se obtiene el valor de Chi-Cuadrado.
4. Finalmente, con el valor de
se verifica que sea menor o igual al valor
obtenido de las Tablas de Distribución Chi-Cuadrado (Anexo 2).
Ejemplo
Digamos que 900 estudiantes expresan su voluntad por celebrar el aniversario de
la institución organizando uno de dos eventos: un acto solemne en el templo
universitario o una actividad deportiva en el estadio de fútbol. Una vez hecha la
encuesta se tiene que 495 alumnos prefieren la actividad deportiva y 405 se inclinan por
el acto solemne. ¿Existe una diferencia significativa entre los estudiantes en su
preferencia por la actividad deportiva?
La prueba estadística para determinar la significatividad de la diferencia en las
frecuencias observadas es la prueba llamada Chi Cuadrado. Para el caso que nos ocupa,
se supone que si no hay diferencia en la preferencia de los alumnos de una manera
perfecta, tendríamos 450 alumnos eligiendo el acto solemne y otros 450 eligiendo las
actividades deportivas.
Esa es la frecuencia de respuestas esperadas en el caso de una igualdad absoluta.
Pero tenemos frecuencias observadas un poco diferentes en un caso son 495 y en el otro
405, lo que deseamos saber es si esa diferencia observada es significativa.
Lo que se hace al aplicar la fórmula de Chi Cuadrado es restar al número de
frecuencias observadas, el número de frecuencias esperadas; elevar esta diferencia al
cuadrado, lo que hace que todos los valores asuman un valor positivo, y luego se divide
57
el cuadrado obtenido entre el las frecuencias esperadas. Esto se hace de manera
independiente para cada una de las categorías. Una vez terminado este paso, se suman
los resultados obtenidos en cada categoría y ese valor resultante de la suma es el valor
Chi Cuadrado observado, el cual deberá ser comparado con el valor Chi Cuadrado
crítico según el nivel
de significatividad escogido y los grados de libertad
correspondientes.
En el caso de nuestro ejemplo se trata de dos categorías, lo que conduce a un
grado de libertad. A continuación el proceso para calcular el valor Chi Cuadrado
A favor del acto solemne:
Frecuencias observadas = 405
Frecuencias esperadas = 450
A favor del acto deportivo:
Frecuencias observadas = 495
Frecuencias esperadas = 450
Se suman los valores obtenidos en cada grupo para obtener el valor de Chi Cuadrado.
58
Se compara este valor con el valor correspondiente a un grado de libertan en la
tabla de Chi Cuadrado (ver anexo 2) y se encuentra que el valor crítico de
grado de libertad a un nivel
para un
a dos colas es = 3.8941.
Siendo que el valor Chi Cuadrado (
) obtenido es mayor que el valor crítico, se
desacredita la hipótesis nula que afirma que no existe diferencia significativa entre las
frecuencias observadas y se concluye que la diferencia es significativa. Esto quiere
decir que en menos de cinco casos de cada cien, una diferencia como la del valor igual o
mayor al observado de Chi Cuadrado, en este caso
, puede ser atribuida a la
selección de la muestra (azar).
4.3.3. Niveles de confianza
El nivel de confianza, es la probabilidad a priori de que el intervalo de confianza
a calcular contenga al verdadero valor del parámetro. Se indica por 1-α y habitualmente
se da en porcentaje (1-α). Hablamos de nivel de confianza y no de probabilidad ya que
una vez extraída la muestra, el intervalo de confianza contendrá al verdadero valor del
parámetro o no, lo que sabemos es que si repitiésemos el proceso con muchas muestras
podríamos afirmar que el (1-α) de los intervalos así construidos contendría al verdadero
valor del parámetro. Que tanta confianza tenemos que la estimación que hicimos de un
intervalo, incluya la mayor parte de la muestra, es decir los casos analizados.
El nivel se significancia de un test es un concepto estadístico asociado a la
verificación de una hipótesis. Se define como la probabilidad de tomar la decisión de
rechazar la hipótesis nula cuando ésta es verdadera. Diferentes valores de α tienen
ventajas y desventajas. Valores pequeños de
α
otorgan mayor confianza en la
determinación de dicha significancia, pero hacen correr mayores riesgos de equivocarse
al rechazar la hipótesis nula falsa.
59
Error tipo I.
Consiste en rechazar una hipótesis nula cuando ésta en realidad, es verdadera.
Recomendaciones para disminuir el error de tipo I:
o Disminuir el número de test estadísticos llevados a cabo en el estudio
o Depurar la base de datos para evitar errores de valores extremos que
puedan producir hallazgos significativos.
o Utilizar valores de alfa más reducidos (0.01 ó 0.001).
o Reproducir el estudio. Si al reproducir el estudio se obtienen resultados
similares, estaremos más seguros de no estar cometiendo el error de tipo
I.
Error tipo II
Este tipo de error, sucede cuando se afirma una hipótesis que de antemano, es falsa.
Recomendaciones para disminuir el error de tipo II:
o Incrementar el tamaño de la muestra.
o Estimar el poder estadístico del estudio.
o Incrementar el tamaño del efecto a detectar.
o Incrementar el valor de alfa.
o Utilizar test paramétricos (más potentes) en lugar de test no
paramétricos.
60
5. Desarrollo del programa
El software contara con dos interfaces de usuario, una para el análisis de fallas y
otra para el análisis de velocidades del viento, las que se detallaran durante el presente
capitulo. El código de programación de cada interface se encuentra en el Anexo 4.
5.1.
MATLAB
El diseño del programa se realizara en base al lenguaje de programación del
software MATLAB, el cual se describe a continuación.
MATLAB (Matrix Laboratory, “laboratorio de matrices”).
Como información general podemos mencionar que MATLAB tiene un modelo
de desarrollo de Software propietario, de genero Software matemático lanzado en 1984.
Este software de ayuda al cálculo está formado por un lenguaje de programación
propio (lenguaje M). Entre sus aplicaciones se hallan: el cálculo matemático de
matrices, manipulación y figuración de datos y funciones, el desarrollo de algoritmos, la
realización de interfaces de usuario (GUI‘s), un entorno de programación visual
(Simulink) y la comunicación con programas en otros lenguajes y con otros dispositivos
hardware. Está disponible para los sistemas operativos Windows, Unix y Apple Mac.
MATLAB dispone de dos aplicaciones adicionales que amplían sus propiedades,
que son: Simulink (plataforma de simulación) y GUIDE (editor de interfaces de usuario
- GUI). Además, se pueden aumentar las características de MATLAB con las
herramientas (toolboxes), y las de Simulink con las aplicaciones de bloques (blocksets).
Este software es utilizado en centros de desarrollo, centros de investigación,
universidades y en empresas de i+d. En estos años se ha ampliado el número de
61
prestaciones, como la de programar directamente procesadores digitales de señal o crear
código VHDL.
Para la creación de las interfaces graficas se recurrirá al uso de la herramienta
GUIDE.
5.2.
Tratamiento de datos
Una vez se obtiene una muestra de tamaño
fundamental a la hora de realizar los análisis
, la organización de los mismos es
respectivos, por esto, es necesario
ordenarlos de forma ascendente como primera medida para el cálculo de los parámetros.
En este primer paso se incluyen todos los valores de tiempos tomados para el
análisis de confiabilidad. Los n valores tomados para el estudio y aproximación, son los
n valores ingresados.
Cuadro N°6. Organización para todos los valores
El segundo paso consiste en agrupar los datos en intervalos, según su frecuencia
para la posterior aplicación de las pruebas de bondad
Una vez sean cargados los datos, se realiza un recorrido fila a fila (los cuales
deben estar en orden ascendente), verificando si cada dato actual es diferente al anterior.
En caso tal que dicho dato sea igual al anterior, lo elimina y continúa con la siguiente
62
fila. Por esto, la cantidad de datos i analizados para el modelo de confiabilidad es
menor o igual que el tamaño total de la muestra de fallos n.
Cuadro N°7. Organización de datos para pruebas de bondad
5.2.1. Nivel de significancia
Es la máxima cantidad de error que estamos dispuestos a aceptar para dar como
validad la hipótesis nula. Se establece convencionalmente en 5%, sin embargo, el
programa cuenta con una serie de posibilidades en cuanto a niveles de significancia los
cuales son decisión del usuario para el tratamiento de los datos que desea realizar
Nivel de significancia del 1%
Nivel de significancia del 5%
Nivel de significancia del 10%
Nivel de significancia del 20%
El nivel de significancia, es una selección del usuario, el cual se encuentra
disponible en la interfaz de usuario, siendo esta un parámetro de entrada.
63
5.3.
Funcionamiento del programa
5.3.1. Diagramas de flujo de cada interfaz
Figura N°20. Diagrama de flujo del programa para el análisis de falla
64
Figura N°21. Diagrama de flujo del programa para el análisis de velocidades del viento
65
5.3.2. Diagramas de flujo discriminados de acuerdo a su función
Diagramas comunes para ambas interfaces:
Selección del tipo de datos
Figura N°22. Diagrama de flujo tipo de datos a analizar
Cargar datos
Figura N°23. Diagrama de flujo de la carga de datos
66
Nivel de significancia
Figura N°24. Diagrama de flujo Nivel de Significancia
Calcular parámetros
Figura N°25. Diagrama de flujo Calcular parámetros
67
Pruebas de bondad de ajuste
Figura N°26. Diagrama de flujo Pruebas bondad de ajuste
68
Diagramas según interfaz
Análisis de fallas
Cálculos posteriores
Figura N°27. Diagrama de flujo del cálculos posteriores análisis de fallas
Gráficas
Figura N°28. Diagrama de flujo del Graficas análisis de fallas
69
Análisis velocidad de viento
Cálculos posteriores
Figura N°29. Diagrama de flujo del Cálculos análisis de viento
Figura N°30. Diagrama de flujo del Cálculo Potencia Aerogenerador
70
Figura N°31. Diagrama de flujo del Gráficas análisis de viento
Los conceptos vistos anteriormente se describirán en mayor detalle en el
subcapítulo siguiente.
Interfaz de usuario
5.4.
La interfaz de usuario, es la comunicación directa entre el usuario y el código
fuente del programa, siendo esta la encargada de mostrar en pantalla todos los
resultados obtenidos durante la ejecución y análisis de una base de datos determinada.
El software posee dos interfaces independientes
para cada tipo de datos
analizar, una para el análisis de fallas y confiabilidad y otra para el análisis de
velocidades del viento y potencial eólico.
En ambas interfaces se presentan los parámetros de la distribución Weibull, si la
hipótesis nula se acepta o rechaza, es decir, si el modelo aproximado para una base de
datos en cuestión puede o no ser simulado como una distribución Weibull, y las
distintas gráficas asociadas a la distribución y a los datos.
El usuario, por medio de la interfaz, está en la obligación de fijar algunos datos
de entrada por medio de un “menú desplegable”, los cuales se realizan directamente en
71
la interfaz y en ambas por igual. El tipo de datos a analizar (análisis de fallas o análisis
de velocidad del viento), el nivel de significancia (0.01, 0.05, 0.1, 0.2) deben ser
determinados antes de comenzar.
5.4.1. Interfaz gráfica para análisis de fallas y confiabilidad
Figura N°32. Interfaz gráfica para el análisis de fallas y tiempos de vida
En la Figura N°32 se puede observar la presentación de la interfaz de usuario, y
todos los elementos que la componen, estos se detallaran según el orden en que deben
ser usados.
Antes que nada deberemos tener claro que tipos de datos analizaremos, en este
caso análisis de fallas como se ve en la Figura N°33.
Este menú desplegable nos permite intercambiar entre las dos interfaces según
los datos a analizar.
72
Figura N°33. Menú desplegable para el tipo de base de datos
Luego deberemos cargar nuestra base de datos mediante el botón “Abrir”, el
cual nos permitirá buscar el archivo Excel en el cual tenemos los datos a analizar.
Figura N°34. Botón “Abrir”
Es necesario señalar que la base de datos debe estar ordenada de una manera
específica para el correcto funcionamiento del software, los detalles se adjuntan en el
Anexo 3.
Teniendo los datos cargados, nos ubicamos en el recuadro denominado
“Parámetros”.
Figura N°35. Sección Parámetros
73
En esta sección debemos seleccionar el nivel de significancia o sensibilidad que
queremos que tengan las pruebas de bondad de ajuste, por defecto de usa 5%, una vez
hecho esto solo nos queda presionar el botón “Calcular Parámetros”.
Figura N°36. Menú desplegable “Nivel de sensibilidad”
Figura N°37. Botón “Calcular Parámetros”
Luego de haber presionado el botón para el cálculo de parámetros, se nos
mostrara la información siguiente; el valor de los parámetros η y β, la media, la
varianza,
y el resultado de las pruebas de bondad Figura N°37, dependiendo del
resultado de estas pruebas tomaremos la decisión de aceptar los parámetros como
válidos, y seguir con los cálculos posteriores, caso contrario la base de datos debe ser
ajustada mediante otras distribuciones no incluidas en el programa.
74
Figura N°38. Información mostrada al calcular parámetros
A parte de la información mencionada, también se graficara automáticamente la
función de densidad de probabilidad al presionar el botón “Calcular Parámetros”.
Figura N°39. Gráfica función de densidad de probabilidad calculada
75
Una vez realizado el cálculo de los parámetros y aceptada la hipótesis, podremos
hacer uso del recuadro “Cálculos” y del menú desplegable de “Gráficas”.
No es posible la utilización de estas secciones sin antes haber calculado los
parámetros, ya que los cálculos realizados en ellas se basan en los parámetros η y β
calculados en la sección anterior. Aclarado esto podemos continuar con la descripción
de la interfaz.
El recuadro “Cálculos” permite al usuario seleccionar entre las distintas
funciones asociadas a la distribución de Weibull y calcularlas dado el valor de una
variable, este valor debe ser ingresado por el usuario en el recuadro blanco superior. El
resultado de la función será mostrado en el recuadro blanco inferior una vez pulsado el
botón “Calcular”.
Figura N°40. Recuadro “Cálculos” Interfaz análisis de fallas
La descripción de cada opción es detallada a continuación:
Confiabilidad: permite el cálculo de la confiabilidad ingresando como variable
el tiempo, la distancia, etc. y entregando el resultado entre 0 y 1.
76
Probabilidad de Falla: entrega el valor entre 0 y 1 de la probabilidad de falla a
través de la función de distribución acumulativa, ingresando para ello el valor de
una variable como tiempo, distancia, etc.
Tiempo Confiable: permite conocer el tiempo u otra variable para un porcentaje
de confiabilidad dado entre 0 y 1.
Tiempo de Falla: permite conocer el tiempo u otra variable para para una
probabilidad de falla dada entre 0 y 1.
Tasa de Fallas: entrega el valor de la tasa de falla según el valor de la variable
que se ingrese.
MTTF/MTTR: muestra el valor correspondiente según el tipo de datos, al no ser
una función solo se selecciona y se presiona el botón “Calcular” para conocer su
valor.
El menú desplegable “Gráficas” permite la visualización de las distintas gráficas
de las funciones indicadas en la Figura N°41.
Figura N°41. Menú desplegable “Gráficas”
La opción PDF grafica la función densidad de probabilidad, y CDF grafica la
función de distribución acumulada, que se corresponde con la opción de probabilidad de
falla del recuadro de “Cálculos”
77
5.4.2. Interfaz para el análisis del potencial eólico
Figura N°42. Interfaz gráfica para el análisis de viento y potencial eólico
En la Figura N°42 se puede observar la presentación de la interfaz de usuario
para el análisis de vientos y potencial eólico, y todos los elementos que la componen,
estos se detallaran según el orden en que deben ser usados.
El menú desplegable para la selección del tipo de datos, el botón “Abrir”, y el
recuadro “Parámetros” no se describirán, ya que su funcionamiento y configuración es
exactamente el mismo que el descrito en la interfaz de análisis de fallas
78
Una vez realizado el cálculo de los parámetros y aceptada la hipótesis, podremos
hacer uso del recuadro “Cálculos”, “Cálculo Potencia Aerogenerador” y del menú
desplegable de “Gráficas”.
No será posible la utilización de estas secciones sin antes haber calculado los
parámetros, ya que los cálculos realizados en ellas se basan en los parámetros η y β
calculados anteriormente. Aclarado esto podemos continuar con la descripción de la
interfaz.
El recuadro “Cálculos” permite al usuario seleccionar entre las distintas
funciones asociadas a la distribución de Weibull y calcularlas dado el valor de una
variable, este valor debe ser ingresado por el usuario en el recuadro blanco superior. El
resultado de la función será mostrado en el recuadro blanco inferior una vez pulsado el
botón “Calcular”. Para la interfaz de análisis de vientos se presentan tres opciones.
Figura N°43. Recuadro “Cálculos” Interfaz análisis vientos
Prob.
: permite conocer la probabilidad de que la velocidad
sea mayor a una velocidad
dada.
Prob. V < v permite conocer la probabilidad de que la velocidad
sea menor a una velocidad
del viento
dada.
del viento
79
P. media disponible: entrega el valor de la potencia media disponible en el
viento en W/m2 solo presionando el botón Calcular.
El cálculo de potencia media generada por un aerogenerador instalado en el
emplazamiento en estudio se realiza mediante el recuadro de la Figura N°44.
Figura N°44. Recuadro “Cálculo Potencia Aerogenerador”
Cargar datos generador: permite buscar y cargar el archivo Excel donde se
encuentran los datos de la curva de potencia del aerogenerador.
Calcular: permite calcular la potencia generada por el aerogenerador integrando
la función que describe la curva de potencia de este y la función de densidad de
probabilidad de la velocidad del viento calculada, entre las velocidades de cut-in
y cut-out entregadas por el fabricante que deben ser ingresadas en los recuadros
correspondientes antes de comenzar el cálculo. La unidad de potencia dependerá
de las unidades en las que se encuentre la curva de potencia del aerogenerador.
La velocidad a la cual el aerogenerador comienza a generar su potencia nominal
(rated power) corresponde a “vr” que encuentra en el recuadro como dato a
ingresar antes del cálculo.
80
El menú desplegable “Gráficas” permite la visualización de las distintas gráficas
de las funciones indicadas en la Figura N°45.
Figura N°45. Recuadro “Gráficas” análisis de vientos
La opción “PDF” grafica la función densidad de probabilidad, y “CDF” grafica
la función de distribución acumulada que se corresponde con “Prob. V < v”, “CDF
Complementaria” que grafica la función de distribución acumulada complementaria y
se corresponde con “Prob.
” y “Curva de Potencia”, que muestra la gráfica de la
curva de potencia del aerogenerador.
81
6. Resultados y Análisis
6.1.
Pruebas de cálculo de parámetros
Se realizó una serie de 25 pruebas en las cuales se generó una base de n datos,
correspondiente a una distribución de Weibull con parámetros η y β dados.
Las pruebas consistieron en calcular los parámetros
de las bases de datos
mediante dos software comerciales, usados para el ajuste de distribuciones de
probabilidad (Weibull++ y Easyfit) y el software diseñado.
En la tabla siguiente se comparan los parámetros calculados con los distintos
programas, además se muestra el número de datos de cada base y sus parámetros reales.
Cuadro N°8. Comparación de parámetros calculados
n η real Β real η W++ β W++ η Easyfit β Easyfit η programa β programa
5
2
1 1.8111 1.3644
1.5772
0.7412
1.8111
1.3644
15
2
5.8 1.9896 4.4985
1.9426
4.0157
1.9896
4.4985
20
3.2
2.7 3.4141 2.4776
3.2212
2.5492
3.4140
2.4775
25
0.5
0.5 0.6599 0.5607
0.6121
0.4715
0.6599
0.5607
32
3.2
0.96 3.7635 1.0049
3.5217
0.9393
3.7635
1.0049
40
1
2 1.0469 1.8417
1.0268
1.6949
1.0469
1.8417
45
0.5
0.5 0.4473 0.4428
0.4121
0.4167
0.4472
0.4428
46
0.5
3.8 0.4962 3.9321
0.4906
3.7940
0.4962
3.9321
46
0.8
2 0.7319 2.2339
0.7427
1.7959
0.7319
2.2340
50
0.5
2.4 0.4367 2.1306
0.4249
2.1638
0.4367
2.1306
52
2.5
6.4 2.4699 5.8031
2.4862
4.9179
2.4699
5.8032
57
3.7
2 3.7569 2.1494
3.6617
2.2136
3.7570
2.1494
62
6.8
2.3 7.0486 2.4615
7.1465
1.9970
7.0485
2.4614
64
3.8
2.9 3.4232 2.6643
3.3894
2.4887
3.4233
2.6644
66
3.5
2.1 3.5234 2.4085
3.5241
2.1173
3.5235
2.4086
74
1.2
1.8 1.2412 1.7552
1.3019
1.2967
1.2412
1.7552
76
0.01
1.3 0.0090 1.2252
0.0089
1.1838
0.0090
1.2252
85
0.1
4 0.1015 3.9852
0.1009
3.9384
0.1015
3.9852
90
1.6
1.4 1.7151 1.3908
1.6787
1.3997
1.7151
1.3909
100
1.4
2 1.3042 1.9613
1.2684
2.1426
1.3042
1.9614
82
112
155
160
270
2
7
10
5
1 1.7678
1.5 6.6859
1 10.0763
5 5.0843
1.0711
1.3950
1.0613
5.1260
1.7145
6.6670
9.8994
5.1235
1.0880
1.3724
1.0962
4.6004
1.7679
6.6859
10.0765
5.0843
1.0711
1.3950
1.0614
5.1260
Se puede ver que los parámetros calculados por el software Weibull++ y los
calculados por el software diseñado son prácticamente iguales, siendo el método de
cálculo de ambos el de Máxima Verosimilitud, en cambio los parámetros calculados por
Easyfit, del cual no se especifica su método de estimación, difieren ligeramente de los
anteriores.
En todas las pruebas la hipótesis nula fue aceptada con un nivel de significancia
de 5%.
Podemos entonces tener la certeza que programa diseñado entrega resultados
consistentes en cuanto a la precisión de los parámetros, estando a la par en este sentido
de los programas comerciales.
6.2.
Aplicaciones prácticas
Se llevaran a cabo una serie de aplicaciones para las cuales se desarrolló el
software y además probar el correcto funcionamiento de este. Estas aplicaciones
consistirán en la resolución de dos ejemplos tanto para un equipo reparable como para
un grupo no reparable, para los cuales se cuenta con sus correspondientes registros
históricos de fallas. Finalmente se realizara un análisis de las distribuciones de vientos
de un emplazamiento del cual se tienen registros de las velocidades del viento durante
un periodo de un año.
83
6.2.1. Análisis de fallas y confiabilidad
Ejemplo 1
El comportamiento de una máquina en el tiempo se muestra en la siguiente
Tabla donde aparecen los distintos tiempos medios entre fallas (TBF) y tiempos de
reparación (TTR). Se desea conocer cuál fue la disponibilidad de la máquina. [19]
Cuadro N°9. Tiempos de falla y tiempos de reparación ejemplo 1
i TBF(Horas) TTR(Horas)
1
110
2
2
330
26
3
120
34
4
220
3
5
225
9
6
218
Cargamos los datos de TBF en el programa y calculamos
Figura N°46. Parámetros tiempos entre fallas ejemplo 1
84
Lo primero que observamos es que las hipótesis nulas de las pruebas de bondad
de ajuste han sido aceptadas, por lo que tomamos los parámetros calculados como
correctos.
Cargamos los datos de TTR en el programa y calculamos
Figura N°47. Parámetros tiempos de reparación ejemplo 1
Observamos que las hipótesis son aceptadas, por lo que tomamos los parámetros
calculados como correctos.
85
Con los datos anteriores podemos calcular la disponibilidad de la máquina como:
Realizando un análisis de confiabilidad podemos calcular la probabilidad de que la
máquina dure más de t horas sin fallos.
]
Por ejemplo:
Figura N°48. Cálculo de confiabilidad usando la interfaz de usuario
]
presente fallos antes de 377,824 es del 1%.
La probabilidad de que la máquina no
86
Figura N°49. Cálculo de confiabilidad usando la interfaz de usuario
]
La probabilidad de que la máquina no
presente fallos antes de 300,883 Horas es del 10%.
Figura N°50. Cálculo de confiabilidad usando la interfaz de usuario
]
La probabilidad de que la máquina no presente
fallos antes de 109,23 Horas es del 90%.
87
Figura N°51. Cálculo de confiabilidad usando la interfaz de usuario
]
La probabilidad de que la máquina no
presente fallos antes de 86,227 Horas es del 95%.
Ejemplo 2
Los datos de la tabla siguiente son esfuerzos de ruptura de 20 conexiones de
alambre, con un extremo soldado sobre un semiconductor y el otro al poste Terminal.
Cada falla consiste en la ruptura del alambre (modo de falla 1 = A) o de una soldadura
(modo de falla 2 = S). En este caso el esfuerzo hace las veces de tiempo de falla. [16]
Cuadro N°10. Esfuerzos y modos de falla ejemplo 2
Esfuerzo
550
750
950
950
1150
1150
1150
1150
1150
1250
1250
Modo
falla
S
A
S
A
A
S
S
A
A
S
S
de
88
1350
1450
1450
1450
1550
1550
1550
1850
2050
A
S
S
A
S
A
A
A
S
Interesa estudiar la distribución del esfuerzo de las conexiones, considerando
que se requiere que menos del 1% debe fallar a un esfuerzo menor a 500 mg. O sea que
al menos el 99% de las conexiones resista un esfuerzo mayor a 500 mg. Se desea
estimar el esfuerzo que resultaría de eliminar uno de los modos de falla.
Primero se hace un análisis sin distinguir los modos de falla, verificando el
ajuste de los datos.
Figura N°52. Parámetros calculados sin considerar modos de fallas
89
Observamos que las hipótesis son aceptadas, por lo tanto los datos pueden ser
modelados por una distribución Weibull con los parámetros indicados:
Haciendo un análisis de confiabilidad para 500 mg considerando los dos tipos de
falla se tiene una confiabilidad de 98,61 %.
Figura N°53. Confiabilidad para esfuerzo de 500 mg.
Y por lo tanto el porcentaje de falla será 1,39% que es mayor al objetivo del
1%, por lo que se tratará de eliminar uno de los modos de falla.
Figura N°54. Probabilidad de falla para esfuerzo de 500 mg.
90
Realizando el análisis por separado para cada modo de falla se tiene:
Modo de falla A
Figura N°55. Parámetros calculados para modo de falla “A”.
Se verifican las hipótesis, aceptándose los parámetros obtenidos.
91
Repitiendo el análisis de confiabilidad para 500 mg considerando el modo de
falla “A” se tiene una confiabilidad de 99,24 %
Figura N°56. Confiabilidad para esfuerzo de 500 mg con modo de falla “A”.
Y por lo tanto el porcentaje de falla será 0,76% el cual es menor al objetivo del
1%, por lo que eliminando el modo de falla “S” es posible lograr la confiabilidad
deseada.
Figura N°57. Probabilidad de falla para esfuerzo de 500 mg con modo de falla “A”.
92
Modo de falla S
Figura N°58. Parámetros calculados para el modo de falla “S”.
Comprobamos que se acepten las hipótesis tomamos los parámetros calculados
como válidos.
Repitiendo el análisis de confiabilidad para 500 mg y considerando el modo de falla
“S” se tiene una confiabilidad de 98,18 %
93
Figura N°59. Confiabilidad para esfuerzo de 500 mg con modo de falla “S”.
Y por lo tanto el porcentaje de falla será 1,82% el cual es mayor al objetivo del
1%, por lo que eliminando el modo de falla “A” y manteniendo el modo de falla “S” no
se logra el nivel de confiabilidad buscado.
Figura N°60. Probabilidad de falla para esfuerzo de 500 mg con modo de falla “S”.
Combinando ambos modos de fallas
En este caso se observa que obtenemos 97.43% de confiabilidad, lo que significa
que el único modo para tener menos de 1% de falla y una confiabilidad mayor a 99%
94
en 500 mg. es eliminando el modo de falla “S” obteniendo así una probabilidad de falla
0,76% y confiabilidad de 99,24%, y cumpliendo con el objetivo.
Como vimos en el ejemplo 2, mediante el programa nos es posible analizar
rápida y fácilmente entre distintos modos de fallas, permitiéndonos conocer como estos
afectan la confiabilidad de algún equipo o componente y la forma en que podemos
mejorarla, en este caso fue eliminando un modo de falla.
También como constatamos en las Figuras N°46 a N°49 del ejemplo 1, con el
programa podemos analizar la confiabilidad para cualquier tiempo que ingresemos y
viceversa, lo que nos permite establecer intervalos de inspección o reemplazo basados
en el valor de la confiabilidad.
6.2.2. Análisis de velocidades de viento y potencial eólico
Se tienen los datos de las velocidades del viento registrados por la estación
meteorológica del laboratorio de Recursos Acuáticos de Calfuco, perteneciente a la
carrera Biología Marina de la Universidad Austral de Chile, estos registros van desde el
01 de Enero de 2006 hasta el 31 de Diciembre de 2006, en intervalos de 1 hora.
Se analizaran los datos para cada uno de los meses del año, para caracterizar de esta
manera el potencial eólico mensual y anual promedio del lugar, y con lo cual determinar
la potencia y energía generadas por un aerogenerador si se instalara en este lugar.
El aerogenerador en estudio será el Acciona AW 70-1500 Class I, de 70 m de
diámetro y 1500 kW. Los datos y curva de potencia del aerogenerador se encuentran el
Anexo 5.
Comenzamos a cargar los datos en el programa y a calcular los parámetros y demás
datos.
95
Enero
Figura N°61. Resultados análisis de velocidades del viento para el mes de Enero
En la Figura N°61 podemos apreciar los parámetros η y β calculados y la hipótesis
se aceptada, por lo tanto tomamos como válidos todos los datos posteriores, además se
puede corroborar observando la gráfica donde se pueden ver el histograma de
frecuencia de los datos reales y la función de densidad de probabilidad calculada, la
cual se ajusta bastante bien a los datos registrados. El mismo análisis se realiza para los
siguientes meses.
La Velocidad media para el mes de enero es de 3,857 m/s
La potencia media disponible del viento es de 231,809 W/m2
La potencia media generada por el aerogenerador en el mes de Enero sería
184,194 kW
96
Y la energía 137.040,336 kWh
Febrero
Figura N°62. Resultados análisis de velocidades del viento para el mes de Febrero
La Velocidad media para el mes de febrero es de 2,356 m/s
La potencia media disponible del viento es de 148,8280 W/m2
La potencia media generada por el aerogenerador en el mes de Febrero sería
91,2830 kW
Y la energía 61.342,176 kWh
97
Marzo
Figura N°63. Resultados análisis de velocidades del viento para el mes de Marzo
La Velocidad media para el mes de marzo es de 2,308 m/s
La potencia media disponible del viento es de 242,003 W/m2
La potencia media generada por el aerogenerador en el mes de Marzo sería
92,112 kW
Y la energía 68.531,328 kWh
98
Abril
Figura N°64. Resultados análisis de velocidades del viento para el mes de Abril
La Velocidad media para el mes de abril es de 3,533 m/s
La potencia media disponible del viento es de 454,9260 W/m2
La potencia media generada por el aerogenerador en el mes de Abril sería
164,1640 kW
Y la energía 118.198,08 kWh
99
Mayo
Figura N°65. Resultados análisis de velocidades del viento para el mes de Mayo
La Velocidad media para el mes de mayo es de 2,810 m/s
La potencia media disponible del viento es de 201,3510 W/m2
La potencia media generada por el aerogenerador en el mes de Mayo sería
118,8480 kW
Y la energía 88.422,912 kWh
100
Junio
Figura N°66. Resultados análisis de velocidades del viento para el mes de Junio
La Velocidad media para el mes de junio es de 4,484 m/s
La potencia media disponible del viento es de 351,8980 W/m2
La potencia media generada por el aerogenerador en el mes de Junio sería
235,2580 kW
Y la energía 169.385,76 kWh
101
Julio
Figura N°67. Resultados análisis de velocidades del viento para el mes de Julio
La Velocidad media para el mes de julio es de 6,115 m/s
La potencia media disponible del viento es de 461,266 W/m2
La potencia media generada por el aerogenerador en el mes de Julio sería
382,1800 kW
Y la energía 284.341,92 kWh
102
Agosto
Figura N°68. Resultados análisis de velocidades del viento para el mes de Agosto
La Velocidad media para el mes de agosto es de 5,225 m/s
La potencia media disponible del viento es de 303,127 W/m2
La potencia media generada por el aerogenerador en el mes de Agosto sería
292,38 kW
Y la energía 217.530,72 kWh
103
Septiembre
Figura N°69. Resultados análisis de velocidades del viento para el mes de Septiembre
La Velocidad media para el mes de septiembre es de 4,032 m/s
La potencia media disponible del viento es de 212,805 W/m2
La potencia media generada por el aerogenerador en el mes de Septiembre sería
192,673 kW
Y la energía 138.724,56 kWh
104
Octubre
Figura N°70. Resultados análisis de velocidades del viento para el mes de Octubre
La Velocidad media para el mes de octubre es de 4,352 m/s
La potencia media disponible del viento es de 237,493 W/m2
La potencia media generada por el aerogenerador en el mes de Octubre sería
217,62 kW
Y la energía 161.909,28 kWh
105
Noviembre
Figura N°71. Resultados análisis de velocidades del viento para el mes de Noviembre
La Velocidad media para el mes de noviembre es de 3,566 m/s
La potencia media disponible del viento es de 162,657 W/m2
La potencia media generada por el aerogenerador en el mes de Noviembre sería
155,315 kW
Y la energía 111.826,8 kWh
106
Diciembre
Figura N°72. Resultados análisis de velocidades del viento para el mes de Diciembre
La Velocidad media para el mes de diciembre es de 4,583 m/s
La potencia media disponible del viento es de 277,212 W/m2
La potencia media generada por el aerogenerador en el mes de Diciembre sería
239,314 kW
Y la energía 178.049,616 kWh
107
En la tabla siguiente se puede apreciar el resumen de la información obtenida
para cada mes, así como también el promedio anual para la velocidad media, potencia
media disponible y la potencia del aerogenerador, además de la energía total generada
durante el año mediante la sumatoria de todos los meses y también calculada usando la
potencia media del generador durante el año.
Cuadro N°11. Resumen anual de la información obtenida.
mes/datos
Enero
Febrero
Marzo
Abril
Mayo
Junio
Julio
Agosto
Septiembre
Octubre
Noviembre
Diciembre
Promedio y
total anual
Velocidad
Potencia media
Potencia media
Media (m/s) disponible (W/m2) aerogenerador (kW)
3,857
231,809
184,194
2,356
148,828
91,283
2,308
242,003
92,112
3,533
454,926
164,164
2,810
201,351
118,848
4,484
351,898
235,258
6,115
461,266
382,180
5,225
303,127
292,380
4,032
212,805
192,673
4,352
237,493
217,620
3,566
162,657
155,315
4,583
277,212
239,314
3,935
273,781
Energía generada (kWh)
137.040,336
61.342,176
68.531,328
118.198,080
88.422,912
169.385,760
284.341,920
217.530,720
138.724,560
161.909,280
111.826,800
178.049,616
Suma
1.735.303,488
Promedio
1.433.880,600
163,685
Anteriormente se estudió la distribución de las velocidades del viento para cada
uno de los meses del año, pero si lo que nos interesa es conocer como es el
comportamiento del viento durante el año completo podemos realizar un análisis único
para todos los datos registrados, cuyo resultado se puede ver en la imagen
108
Figura N°73. Resultados análisis de velocidades del viento para el año 2006
De la Figura N°73 obtenemos la misma información que obtuvimos en los
análisis mensuales anteriores, pero esta vez aplicados al año completo.
La Velocidad media del año 2006 fue de 4,014 m/s
La potencia media disponible del viento para el año 2006 fue de 320,633 W/m2
La potencia media generada por el aerogenerador sería 199,543 kW
Y la energía producida durante el año 1.747.996,680 kWh
En el Cuadro N°11 podemos ver que en los meses Julio y Agosto están presentes
las velocidades medias más altas, coincidiendo para el mes de Julio con potencia media
109
más alta, pero no así para el mes de Agosto, que a pesar de tener la segunda mayor
velocidad media no se corresponde con la segunda mayor potencia media, la cual tiene
lugar en el mes de abril. Esto ocurre debido a la distribución que presentan los vientos
en estos meses, siendo abril el mes que mayor potencia media presenta frente al mes de
Agosto, pero gran parte de esta potencia es debida a vientos de bajas velocidades, los
cuales no son aprovechables por el aerogenerador, por esto mismo vemos que la
potencia generada por el aerogenerador para el mes de Agosto es mayor que la del mes
de Abril, a pesar de que la potencia disponible del viento es mayor.
En cuanto a la energía generada anualmente obtenemos diferencias si la
calculamos mes a mes o si la calculamos con la potencia promedio anual del generador
obtenida de la tabla, para la primera obtenemos 1.735.303,488 kWh al año como se ve
en la tabla, pero para la segunda opción obtenemos 1.433.880,6 kWh al año, una
diferencia de 301.422,888 kWh lo que representa un 17.37%. Dado lo anterior se
prefiere el cálculo mes a mes por ser más representativo.
Se debe aclarar que la velocidad, potencia disponible y potencia generada
medias del Cuadro N°11 son calculadas directamente desde la tabla. Para tener unos
valores más representativos es necesario hacer el análisis que se ve en la Figura N°73.
Comprobamos que la información obtenida del análisis del año completo de la
Figura N°73 son bastante más representativos que los promedios obtenidos del Cuadro
N°11, esto lo podemos hacer comparando la energía generada durante el año, obtenida
de tres formas distintas siendo la más cercana a la realidad la sumatoria que se hace mes
a mes.
Haciendo lo indicado en el párrafo anterior tenemos:
La energía calculada mediante el análisis de cada uno de los meses es de
1.735.303,488 kWh/año, la energía calculada con la potencia media generada del
Cuadro N°11, que tiene un valor de 163,685 kW es de 1.433.880,600 kWh/año,
110
finalmente haciendo el análisis para todo el año que se observa en la Figura N°73
obtenemos otro valor de potencia media generada el cual es 199,543 kW, con la que se
obtiene una energía generada de 1.747.996,680 kWh como podemos ver a simple vista
bastante cercana a nuestro valor de referencia. Para una mejor claridad se presentan
estos valores en la siguiente tabla.
Valor de referencia: 1.735.303,488 kWh/año
Cuadro N°12. Comparación cálculo energías generadas
Potencia media (kW) Horas/año kWh/año
Error absoluto Error relativo
8760 1.433.880,600
301.422,888
0,1737
163,685
8760 1.747.996,680
12.693,192
0,0073
199,543
Con lo anterior se verifica que las medias anuales calculadas mediante el
software son mucho más representativas en relación al valor de referencia, con un error
de 0,73% frente al 17,37% del valor calculado desde la tabla.
Como se observó en los resultados anteriores, el análisis de diferentes datos
aplicados a un estudio en concreto se realiza de manera rápida y sencilla, solo cargando
los datos que se desean analizar, seleccionar el nivel de sensibilidad o significancia y
presionando el botón “Calcular Parámetros” , mediante lo cual el software realiza el
cálculo automáticamente, entregando el resultado de los parámetros, la media y
varianza, además de la gráfica de la función densidad de probabilidad, que se obtiene a
través de los parámetros calculados.
En cuanto al análisis de las distribuciones de la velocidad del viento, se puede
apreciar que en cada captura de la interfaz se entregan los datos necesarios para la
estimación del potencial eólico de cada mes, y fácilmente se pueden agrupar estos
datos en una tabla, en la cual tener un resumen anual.
111
Cabe indicar que en la sección del generador, una vez cargados los datos de este,
se pueden dejar en espera, con lo cual se evita estar cargando los datos del generador
cada vez que se realice el análisis de otro mes o año según corresponda, para el caso
práctico anterior se realizó de este modo ahorrando bastante tiempo. Lo anteriormente
mencionado sobre mantener en espera los datos del generador, es aplicable también de
forma inversa, esto quiere decir, que es posible probar distintos modelos de
aerogeneradores para un mismo mes, sin la necesidad de estar cargando y calculando
constantemente los datos del mes en estudio
aerogenerador.
cada vez que se seleccione otro
112
7. Conclusiones
El análisis de fallas mediante métodos estadísticos es una es una poderosa
herramienta para la gestión del mantenimiento, pero la calidad de la información
obtenida por estos análisis dependerá en gran medida, de la recolección de los datos, de
la forma en que estos son registrados, y de que tan reales sean. En otras palabras el
resultado de estos análisis será tan confiable como lo sean los datos registrados.
Al realizar un análisis estadístico basado en los tiempos de falla, es
indispensable establecer los tipos de datos que se poseen para el análisis, es por esto
que se hace necesario realizar un tratamiento a la información recolectada, como
diferenciar tiempos de fallas de tiempos de reparación, diferenciar entre distintos
modos de fallas y sus tiempos correspondientes entre otros, todo esto para brindar con
una organización de los datos que permita la correcta selección de la distribución, con
el fin de tener una aproximación más cercana y fiel, y así una correcta interpretación de
los resultados.
La aplicación de la distribución de Weibull se ha vuelto más popular
últimamente en gran medida gracias al avance de la tecnología en cuanto a
herramientas de cálculo, y programas especializados. Históricamente siempre fue
dejada de lado frente a otras distribuciones, por la dificultad en el cálculo de sus
parámetros. Actualmente realizar la estimación del potencial eólico de un año completo
en pocos pasos y en poco tiempo, analizar distintos modos de fallas y ver cómo afectan
a la confiabilidad, solo cargando otra base de datos, significa un gran avance
comparado con el método grafico clásico de Weibull, o la aproximación mediante otras
distribuciones que no siempre se ajustan de la mejor manera a los datos.
El software diseñado es capaz de entregar resultados a la altura de otros software
comerciales especializados, en la precisión de los parámetros, como se observó en la
comparación del cálculo con otros dos programas, además de la claridad en la
presentación de los resultados para su interpretación.
Es importante señalar, que para la correcta interpretación de los datos
proporcionados por el programa es indispensable el conocimiento y manejo de los
términos y conceptos involucrados, tanto de mantenimiento, de energía eólica, y de
estadística.
El software diseñado se basa en el cálculo de los parámetros η y β para la
obtención de la función de densidad de probabilidad (PDF), de la cual al ser integrada
se obtienen todas las otras funciones relacionadas para su aplicación, como la función
de distribución acumulativa que se utiliza en los ejemplos de análisis de fallas y
confiabilidad para calcular las probabilidades de fallas, la función de confiabilidad o
113
distribución acumulada complementaria, que es usada en el mismo ejemplo para
conocer el valor de la confiabilidad.
Cabe resaltar que la distribución Exponencial, la distribución de Rayleigh, y la
distribución Normal al ser casos particulares de la distribución de Weibull están
incluidas en esta, por lo tanto el software diseñado tiene la capacidad de tratar bases de
datos provenientes de dichas distribuciones y calcularlas mediante la distribución de
Weibull, algunos de estos casos se dan en el análisis de los TTR del ejemplo 1 de
análisis de falla y confiabilidad y en los meses de Enero, Junio, Agosto y Noviembre
del análisis de velocidades del viento, donde las distribuciones se aproximan a una
distribución exponencial.
Por lo indicado anteriormente es muy difícil que el software rechace una base de
datos, ya que por lo general los tiempos de fallas y velocidades del viento tienen un
comportamiento que es modelable mediante estas distribuciones, al ser variables
aleatorias continuas.
Con respecto a los objetivos, finalmente se logró dar cumplimiento al objetivo
general de este proyecto, obteniendo un software funcional y capaz de calcular los
parámetros buscados y de entregar información consistente de acuerdo a las necesidades
del usuario.
La principal ventaja del software es la de ser un software libre, sin la necesidad
de pagar una licencia por su uso permanente, ciertamente existen otros programas que
podrían denominarse como “libres” al alcance de cualquier persona, como lo son
Excel o el mismísimo MATLAB en el cual se basa el programa diseñado, pero estos
requieren necesariamente varios pasos previos tanto para calcular y graficar, además de
la necesidad de conocer el lenguaje de programación de ambos, inconvenientes que con
la interfaz de usuario del programa desarrollado se eliminan.
114
Bibliografía
[1] Barragán Guerrero Diego Orlando; “Manual de interfaz gráfica de usuario en
MATLAB”, Disponible:
http://www.dspace.espol.edu.ec/bitstream/123456789/10740/19/%255Bmatlab%255D_
MATLAB_GUIDE.pdf
[2] Barón López Francisco Javier, Parras Guijosa Luis, Ríus Díaz Francisca, Sánchez
Font Elisa; Manual Bioestadística: Métodos y Aplicaciones, 3ª Edición. Facultad de
Medicina Universidad de Málaga. Málaga, España.
[3] Bonoli Escobar Mariano, Bufanio Ruben, Edwards Diego, Gogni Valeria;
Estimación de Potencial Anual Generada por un Generador Eólico, Seminario Nacional
Universidad Tecnológica Nacional, Eficiencia Energética, Mendoza, Argentina, 2012.
[4] Canales Rojas Javiera Alejandra; Diseño y control estadístico de la fractura de
materiales; Tensión de adherencia de estuco de cal sobre adobe (tesis de grado),
Universidad de Chile, Santiago, Chile, Diciembre, 2009.
[5] Cervantes Hernández Pedro, Flores Gómez
Andrea,
Sánchez Meraz Blanca;
Mínimos cuadrados versus verosimilitud, Revista Ciencia y Mar, Universidad del Mar,
Puerto Ángel, México, N° 27, pp. 41-45, 2005.
[6] Dickinson Gibbons Jean, Chakraborti Subhabrata;
Nonparametric Statistical
Inference. Fourth Edition, Marcel Dekker, Inc., New York, USA, 2003.
[7] Hernández Figueroa Esther,
Pérez Soto Francisco, Rojano Aguilar Abraham,
Salazar Moreno Raquel; Aplicaciones de la distribución Weibull en ingeniería de
confiabilidad, Memoria del XXI Coloquio Mexicano de Economía Matemática y
Econometría, Universidad Autónoma de Nayarit, Nayarit, México, 2011.
115
[8] González Fernández, F. J.; “Teoría y Práctica del Mantenimiento Industrial
Avanzado”, 2ª edición, FUNDACIÓN CONFEMETAL, Madrid, España, 2005.
[9] J. Pascual Rodrigo; Manual del Ingeniero de Mantenimiento. Gestión Moderna del
Mantenimiento Versión 2.0, Universidad. de Chile, Santiago, Chile, Julio 2002.
[10] Martínez Fernández Laura; Métodos de inferencia para la distribución Weibull:
Aplicación en fiabilidad industrial, Trabajo fin de Master, Universidad de Vigo, Vigo,
España, Julio de 2011.
[11] Murillo William; “Confiabilidad y análisis estadístico para la predicción de fallas,
seguridad, supervivencia, riesgo, costo y garantía de los equipos” Disponible:
http://www.rcmingenieria.com/sites/default/files/4.14%20Weibull%20Analisis%20para
%20prediccion%20de%20fallas%20Ver1.pdf
[12] Orrego Barrera Juan Carlos; “Estadística y la Gestión del Mantenimiento”,
Disponible:
http://www.slideshare.net/mantonline/estadstica-y-la-gestion-del-
mantenimiento
[13] Palacio Palacio Luis Hernando; “Cálculo de los Parámetros de la Distribución de
Weibull” Disponible: http://confiabilidad.net/articulos/calculo-de-los-parametros-de-ladistribucion-de-weibull/
[14] Pistarelli Alejandro J.; Manual de Mantenimiento: Ingeniería, Gestión, y
Organización, 1ª Edición, RyC, Argentina, 2010.
[15]
Poujol
Galván
Francisco;
“Distribución
Weibull”
http://confiabilidad.net/articulos/distribucion-weibull/
[16] Reyes Aguilar Primitivo; Curso de Confiabilidad, Diciembre de 2006
Disponible:
116
[17] Rodríguez Huertas Rosa, Gámez Mellado Antonio, Marín Trechera Luis y Fandiño
Patiño Santiago; Estadística Industrial (Temas de estadística para Ingenieros), Escuela
Superior de Ingeniería, Universidad de Cádiz, Cádiz, España, Diciembre de 2005.
[18] Rodríguez Ojeda Luis; Probabilidad y Estadística Básica para Ingenieros con
soporte de MATLAB para cálculos y gráficos estadísticos, Escuela Superior Politécnica
del Litoral, Guayaquil, Ecuador, 2007.
[19] Romero López Eduardo; Estudio de mejora del mantenimiento mediante la
aplicación de la distribución de Weibull a un histórico de fallos (proyecto fin de
postgrado), Universidad Nacional de Educación a Distancia UNED, Madrid, España, 4
de Septiembre de 2012.
[20]
Santos
M.;
“Distribuciones
estadísticas
con
MATLAB”
Disponible:
http://grupo.unavirtual.una.ac.cr/mahara/artefact/file/download.php?file=6827&view=1
085
[21] Serrano Rico Juan Carlos; Comparación de métodos para determinar los
parámetros de Weibull para la generación de energía eólica, Articulo Revista Scientia et
Technica, Universidad Tecnológica de Pereira, Pereira, Colombia, Año XVIII, Vol. 18,
N° 2, Agosto 2013.
[22] Verdin Medina Luis Armando; Estimación de Máxima Verosimilitud en la
distribución Weibull para muestras completas, censuradas y su aplicación en el análisis
de tiempos de vida (tesis de grado), Universidad Autónoma Chapingo, Chapingo,
México, Marzo del 2005.
[23] Villarrubia López Miguel; Ingeniería de la Energía Eólica, 1ª Edición,
MARCOMBO S.A., Barcelona, España, 2012.
[24] Weibull Waloddi, A Statistical Distribution Function of Wide Applicability, 1951.
117
[25] “Prueba de Bondad de Ajuste de Kolmogorov-Smirnov (KS)”; Disponible:
https://www.ulpgc.es/hege/almacen/download/5/5015/Complemento_3_Prueba_de_Bon
dad_de_Ajuste_de_Kolmogorov_Smirnov.pdf
[26] Página web del Grado de Ingeniería en Energías Renovables de la Universidad del
País Vasco, sección MATLAB para el Grado en Ingeniería de Energías Renovables,
Estadística
del
Viento.
Disponible:
http://www.sc.ehu.es/sbweb/energias-
renovables/MATLAB/numerico/analisis-datos/analisis-datos.html
[27] Página web de MATLAB, http://www.mathworks.com/products/matlab/
[28] Curso energía eólica Endesa, Principios de la energía eólica, Septiembre de 2007.
Disponible: http://www.escuelaendesa.com/pdf/2_PRINCIPIOS%20DE%20LA%20
ENERGIA%20E%C3%93LICA.pdf
118
Anexo 1
Distribución del estadístico de Kolmogorov-Smirnov
119
Anexo 2
Tabla de distribución Chi-Cuadrado
120
Anexo 3
Forma en que deben estar los datos para su análisis mediante el software desarrollado
1
2
3
4
5
6
7
8
9
10
.
.
.
n
m1
m2
m3
m4
m5
m6
m7
m8
m9
m10
.
.
.
mn
En la primera columna se ubican el orden de los datos, los cuales van desde 1
hasta n coincidiendo con el total de datos registrados.
En la segunda columna se ubican los datos registrados para su análisis, estos van
desde m1 a mn coincidiendo con la cantidad de filas de la columna 1.
Cabe indicar que el orden de los datos de la columna 2 no interesa, ya que el
programa se encarga de ordenarlos automáticamente.
Este mismo ordenamiento aplica a la tabla de potencias del aerogenerador.
121
Anexo 4
El texto en color verde corresponde a comentarios y no tiene ninguna influencia
en el funcionamiento del código.
Código de programación interfaz análisis de fallas y confiabilidad
function varargout = programaweibull(varargin)
% PROGRAMAWEIBULL MATLAB code for programaweibull.fig
%
PROGRAMAWEIBULL, by itself, creates a new PROGRAMAWEIBULL or
raises the existing
%
singleton*.
%
%
H = PROGRAMAWEIBULL returns the handle to a new PROGRAMAWEIBULL
or the handle to
%
the existing singleton*.
%
%
PROGRAMAWEIBULL('CALLBACK',hObject,eventData,handles,...) calls
the local
%
function named CALLBACK in PROGRAMAWEIBULL.M with the given
input arguments.
%
%
PROGRAMAWEIBULL('Property','Value',...) creates a new
PROGRAMAWEIBULL or raises the
%
existing singleton*. Starting from the left, property value
pairs are
%
applied to the GUI before programaweibull_OpeningFcn gets
called. An
%
unrecognized property name or invalid value makes property
application
%
stop. All inputs are passed to programaweibull_OpeningFcn via
varargin.
%
%
*See GUI Options on GUIDE's Tools menu. Choose "GUI allows
only one
%
instance to run (singleton)".
%
% See also: GUIDE, GUIDATA, GUIHANDLES
% Edit the above text to modify the response to help programaweibull
% Last Modified by GUIDE v2.5 02-Nov-2013 17:01:09
% Begin initialization code - DO NOT EDIT
gui_Singleton = 1;
gui_State = struct('gui_Name',
mfilename, ...
'gui_Singleton', gui_Singleton, ...
'gui_OpeningFcn', @programaweibull_OpeningFcn, ...
'gui_OutputFcn', @programaweibull_OutputFcn, ...
'gui_LayoutFcn', [] , ...
'gui_Callback',
[]);
if nargin && ischar(varargin{1})
gui_State.gui_Callback = str2func(varargin{1});
122
end
if nargout
[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});
else
gui_mainfcn(gui_State, varargin{:});
end
% End initialization code - DO NOT EDIT
%Menú desplegable tipo de datos
function interfaces_Callback(hObject, eventdata, handles)
valor_interfaces=get(handles.interfaces,'Value');
switch valor_interfaces
case 2
clear all; close all;clc; Vientos;
end;
%------------------------------------------------------------%-------------------------------------------------------------
%Botón abrir
function botonabrir_Callback(hObject, eventdata, handles)
%buscar y cargar archivo con los datos
[FileName Path]=uigetfile({'*.xlsx'},'Abrir Documento');
%guarda datos para usarlos en otras funciones
handles.archivo = xlsread(fullfile(Path, FileName));
guidata(hObject, handles);
%--------------------------------------------------------------------%---------------------------------------------------------------------
%Menú desplegable Nivel Sensibilidad
function ns_Callback(hObject, eventdata, handles)
valor_ns=get(handles.ns,'Value');
Nivel=0;
switch valor_ns;
case 1
ns=0.05
Nivel=ns;
handles.nivel=Nivel;
guidata (hObject,handles);
123
case 2
ns = 0.01;
Nivel=ns;
handles.nivel=Nivel;
guidata (hObject,handles);
case 3
ns=0.05;
Nivel=ns;
handles.nivel=Nivel;
guidata (hObject,handles);
case 4
ns=0.1;
Nivel=ns;
handles.nivel=Nivel;
guidata (hObject,handles);
case 5
ns=0.2;
Nivel=ns;
handles.nivel=Nivel;
guidata (hObject,handles);
end;
%--------------------------------------------------------------------%---------------------------------------------------------------------
%Boton Calcular parámetros
function calcula_Callback(hObject, eventdata, handles)
NUMERIC=handles.archivo;
NS=4;
i = size(NUMERIC,1);
x = (NUMERIC(1,1));
Ks = zeros(i,1);
xx=1;
while xx <= i,
y = (NUMERIC(xx,2));
Ks(xx,1)= y;
KS = sort((Ks(:))); %Ordena de menor a mayor
xx = xx + 1;
end
%Parámetros por Máxima Verosimilitud
124
parmhat = wblfit(Ks);
AlfaMV = parmhat (1,1); %parámetro eta
BetaMV = parmhat (1,2); %parámetro beta
[M,V] = wblstat(AlfaMV,BetaMV);
AlfaMV;
BetaMV ;
M; % Media
V; %Varianza
alfaa=AlfaMV
betaa=BetaMV
handles.alfaa=alfaa;
guidata (hObject,handles);
handles.betaa=betaa;
guidata (hObject,handles);
handles.Ks=Ks;
guidata (hObject,handles);
set(handles.alfa,'String',AlfaMV);
set(handles.beta,'String',BetaMV);
set(handles.media,'String',M);
set(handles.varianza,'String',V);
%Cálculos para graficas
KS = sort((Ks(:))); %Ordena de menor a mayor
n = 1;
FTW=zeros(i,1);
FCUM=zeros(i,1);
FTWEXP=zeros(i,1);
FCUMEXP=zeros(i,1);
KS;
kaese=KS;
handles.KS=kaese;
guidata (hObject,handles);
while n<=i,
t = (KS(n,1));
Ftw = ((BetaMV*(t^(BetaMV-1)))/(AlfaMV^BetaMV))*
(exp(- (t/AlfaMV)^(BetaMV)));
FTW(n,1)=Ftw;
Fcum = (1 - (exp(-(t/AlfaMV)^(BetaMV))));
FCUM(n,1) = Fcum;
Conf = (exp(-(t/AlfaMV)^(BetaMV)));
CONF(n,1) = Conf;
n = n+1;
end
cdf=FCUM;
handles.FCUM=cdf;
guidata (hObject,handles);
125
confiabilidad=CONF
handles.CONF=confiabilidad;
guidata (hObject,handles);
%--------------------------------------------------------------------%Grafica PDF
tt=linspace(0,max(KS),100);
f2=@(tt) (BetaMV/AlfaMV)*((tt/AlfaMV).^(BetaMV-1)).*exp((tt/AlfaMV).^BetaMV);
axes(handles.graf);
cla reset;
x=min(KS):0.1:max(KS);
f = wblpdf(x,AlfaMV,BetaMV);
plot(x,f,'r');
plot(tt,f2(tt),'r')
hold off
set(handles.graf, 'xgrid', 'on', 'ygrid', 'on');
%---------------------------------------------------------------------
%--------------------------------------------------------------------%Pruebas bondad de ajuste
%tratamiento de datos
Numeric1 = handles.archivo;
Numeric2 = sort(Numeric1);
ii2 = size (Numeric1,1);
iii2=1;
n2=1;
Datosfrec=zeros(n2,2);
Datosfrec (n2,1) = n2;
if iii2==1,
Datosfrec (n2,2) = Numeric2 (iii2,2);
iii2=iii2+1;
n2=n2+1;
Datosfrec (n2,1) = n2;
end;
while iii2<=ii2,
if Numeric2 (iii2,2) == Numeric2 (iii2-1,2);
else
Datosfrec (n2,2) = Numeric2 (iii2,2);
Datosfrec (n2,1) = n2;
n2=n2+1;
end;
iii2=iii2+1;
end;
Datosfrec1=Datosfrec(:,2);
pd = fitdist(Datosfrec1,'Weibull');
126
% según nivel de sensibilidad seleccionado
Nivel=handles.nivel;
if Nivel==0.05,
NS=0.05;
else
if Nivel==0.01,
NS=0.01;
else
if Nivel==0.05,
NS=0.05;
else
if Nivel==0.1,
NS=0.1;
else
if Nivel==0.2,
NS=0.2;
end;
end;
end;
end;
end;
%Kolmogorov-Smirnov
kolmogorov = kstest(Datosfrec1,'CDF',pd,'Alpha',NS)
if kolmogorov==0,
'La Hipótesis se acepta'
else
'La Hipótesis se rechaza'
end;
set(handles.hipo1,'String',ans);
% Chi-Cuadrado
chicuadradoo = chi2gof(Datosfrec1,'CDF',pd,'Alpha',NS)
if chicuadradoo==0,
'La Hipótesis se acepta'
else
'La Hipótesis se rechaza'
end;
set(handles.hipo2,'String',ans);
end;
127
end;
%--------------------------------------------------------------------%---------------------------------------------------------------------
%Recuadro calculus
%opciones
function uipanel9_SelectionChangeFcn(hObject, eventdata, handles)
if hObject == handles.conf
op=1;
handles.op=op;
guidata (hObject,handles);
elseif hObject == handles.probf
op=2;
handles.op=op;
guidata (hObject,handles);
elseif hObject == handles.tiempc
op=3;
handles.op=op;
guidata (hObject,handles);
elseif hObject == handles.tiempf
op=4;
handles.op=op;
guidata (hObject,handles);
elseif hObject == handles.tasa
op=5;
handles.op=op;
guidata (hObject,handles);
elseif hObject == handles.mtbf
op=6;
handles.op=op;
guidata (hObject,handles);
end;
%botón calcular del recuadro cálculos
function calculos_Callback(hObject, eventdata, handles)
opcion= handles.op;
AlfaMV=handles.alfaa;
BetaMV=handles.betaa;
if opcion==1,
get(handles.dato,'String');
num = str2double(get(handles.dato,'String'));
t=num;
Conf = (exp(-(t/AlfaMV)^(BetaMV)));
set(handles.resultado,'String',Conf);
128
end;
if opcion==2,
get(handles.dato,'String');
num = str2double(get(handles.dato,'String'));
t=num;
Fcum = (1 - (exp(-(t/AlfaMV)^(BetaMV))));
set(handles.resultado,'String',Fcum);
end;
if opcion==3,
get(handles.dato,'String');
num = str2double(get(handles.dato,'String'));
Conf=num;
t=AlfaMV*((-log(Conf))^(1/BetaMV))
set(handles.resultado,'String',t);
end;
if opcion==4,
get(handles.dato,'String');
num = str2double(get(handles.dato,'String'));
Fcum=num;
t=AlfaMV*((-log(1-Fcum))^(1/BetaMV))
set(handles.resultado,'String',t);
end;
%tasa de fallas
if opcion==5,
get(handles.dato,'String');
num = str2double(get(handles.dato,'String'));
t=num;
h=(((BetaMV*(t^(BetaMV-1)))/(AlfaMV^BetaMV))*
(exp(-(t/AlfaMV)^(BetaMV))))/(exp(-(t/AlfaMV)^(BetaMV)));
set(handles.resultado,'String',h);
end;
if opcion==6,
MTBF=AlfaMV*(gamma(1+(1/BetaMV)));
set(handles.resultado,'String',MTBF);
end;
%--------------------------------------------------------------------%--------------------------------------------------------------------%menú desplegable gráficas
function graficos_Callback(hObject, eventdata, handles)
valor_graficos=get(handles.graficos,'Value');
AlfaMV=handles.alfaa;
BetaMV=handles.betaa;
KS=handles.KS;
FCUM=handles.FCUM;
CONF=handles.CONF;
129
switch valor_graficos
case 1
tt=linspace(0,max(KS),100);
f2=@(tt) (BetaMV/AlfaMV)*((tt/AlfaMV).^(BetaMV-1)).*exp((tt/AlfaMV).^BetaMV);
%Grafica PDF
axes(handles.graf);
cla reset;
x=min(KS):0.1:max(KS);
f = wblpdf(x,AlfaMV,BetaMV);
hold on
plot(x,f,'r');
plot(tt,f2(tt),'r')
hold off
set(handles.graf, 'xgrid', 'on', 'ygrid', 'on');
case 2
%Grafica CDF
axes(handles.graf)
cla reset;
hold on
x=min(KS):1:max(KS);
f = wblcdf(x,AlfaMV,BetaMV); %linea
plot(x,f);
plot(KS,FCUM,'x');
%puntos
hold off
set(handles.graf, 'xgrid', 'on', 'ygrid', 'on');
case 3
%Grafica confiabilidad
axes(handles.graf)
cla reset;
hold on
plot(min(KS):1:max(KS),1cdf('wbl',min(KS):1:max(KS),AlfaMV,BetaMV)); %linea
plot(KS,CONF,'x');
%puntos
hold off
set(handles.graf, 'xgrid', 'on', 'ygrid', 'on');
case 4
%Grafica tasa de fallas
h= (pdf./CONF)
axes(handles.graf)
cla reset;
hold on
plot(KS,h)
hold off
set(handles.graf, 'xgrid', 'on', 'ygrid', 'on');
end;
%--------------------------------------------------------------------%---------------------------------------------------------------------
130
Código de programación interfaz análisis de vientos y potencial eólico
function varargout = Vientos(varargin)
% VIENTOS MATLAB code for Vientos.fig
%
VIENTOS, by itself, creates a new VIENTOS or raises the
existing
%
singleton*.
%
%
H = VIENTOS returns the handle to a new VIENTOS or the handle
to
%
the existing singleton*.
%
%
VIENTOS('CALLBACK',hObject,eventData,handles,...) calls the
local
%
function named CALLBACK in VIENTOS.M with the given input
arguments.
%
%
VIENTOS('Property','Value',...) creates a new VIENTOS or raises
the
%
existing singleton*. Starting from the left, property value
pairs are
%
applied to the GUI before Vientos_OpeningFcn gets called. An
%
unrecognized property name or invalid value makes property
application
%
stop. All inputs are passed to Vientos_OpeningFcn via
varargin.
%
%
*See GUI Options on GUIDE's Tools menu. Choose "GUI allows
only one
%
instance to run (singleton)".
%
% See also: GUIDE, GUIDATA, GUIHANDLES
% Edit the above text to modify the response to help Vientos
% Last Modified by GUIDE v2.5 03-Nov-2013 23:24:43
% Begin initialization code - DO NOT EDIT
gui_Singleton = 1;
gui_State = struct('gui_Name',
mfilename, ...
'gui_Singleton', gui_Singleton, ...
'gui_OpeningFcn', @Vientos_OpeningFcn, ...
'gui_OutputFcn', @Vientos_OutputFcn, ...
'gui_LayoutFcn', [] , ...
'gui_Callback',
[]);
if nargin && ischar(varargin{1})
gui_State.gui_Callback = str2func(varargin{1});
end
if nargout
[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});
else
gui_mainfcn(gui_State, varargin{:});
131
end
% End initialization code - DO NOT EDIT
% --- Executes just before Vientos is made visible.
function Vientos_OpeningFcn(hObject, eventdata, handles, varargin)
% This function has no output args, see OutputFcn.
% hObject
handle to figure
% eventdata reserved - to be defined in a future version of MATLAB
% handles
structure with handles and user data (see GUIDATA)
% varargin
command line arguments to Vientos (see VARARGIN)
% Choose default command line output for Vientos
handles.output = hObject;
% Update handles structure
guidata(hObject, handles);
% UIWAIT makes Vientos wait for user response (see UIRESUME)
% uiwait(handles.figure1);
% --- Outputs from this function are returned to the command line.
function varargout = Vientos_OutputFcn(hObject, eventdata, handles)
% varargout cell array for returning output args (see VARARGOUT);
% hObject
handle to figure
% eventdata reserved - to be defined in a future version of MATLAB
% handles
structure with handles and user data (see GUIDATA)
% Get default command line output from handles structure
varargout{1} = handles.output;
% --- Executes during object creation, after setting all properties.
function popupmenu1_CreateFcn(hObject, eventdata, handles)
% hObject
handle to popupmenu1 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles
empty - handles not created until after all CreateFcns
called
% Hint: popupmenu controls usually have a white background on Windows.
%
See ISPC and COMPUTER.
if ispc && isequal(get(hObject,'BackgroundColor'),
get(0,'defaultUicontrolBackgroundColor'))
set(hObject,'BackgroundColor','white');
end
%--------------------------------------------------------------------%--------------------------------------------------------------------%menú desplegable tipo de datos
function interfaces_Callback(hObject, eventdata, handles)
valor_interfaces=get(handles.interfaces,'Value');
switch valor_interfaces
case 2
clear all; close all;clc; programaweibull;
end;
132
%--------------------------------------------------------------------%--------------------------------------------------------------------%botón abrir
function pushbutton3_Callback(hObject, eventdata, handles)
[FileName Path]=uigetfile({'*.xlsx'},'Abrir Documento'); %buscar y
cargar archivo con los datos
handles.archivo = xlsread(fullfile(Path, FileName)); %guarda datos
para usarlos en otras funciones
guidata(hObject, handles);
%--------------------------------------------------------------------%--------------------------------------------------------------------%menú desplegable nivel sensibilidad
function ns_Callback(hObject, eventdata, handles)
valor_ns=get(handles.ns,'Value');
Nivel=0;
switch valor_ns;
case 1
ns=0.05
Nivel=ns;
handles.nivel=Nivel;
guidata (hObject,handles);
case 2
ns = 0.01;
Nivel=ns;
handles.nivel=Nivel;
guidata (hObject,handles);
case 3
ns=0.05;
Nivel=ns;
handles.nivel=Nivel;
guidata (hObject,handles);
case 4
ns=0.1;
Nivel=ns;
handles.nivel=Nivel;
guidata (hObject,handles);
case 5
ns=0.2;
Nivel=ns;
handles.nivel=Nivel;
guidata (hObject,handles);
133
end;
%--------------------------------------------------------------------%--------------------------------------------------------------------function calcula_Callback(hObject, eventdata, handles)
NUMERIC=handles.archivo;
NS=4;
i = size(NUMERIC,1);
x = (NUMERIC(1,1));
Ks = zeros(i,1);
xx=1;
yy=i;
handles.i=yy;
guidata (hObject,handles);
while xx <= i,
y = (NUMERIC(xx,2));
Ks(xx,1)= y;
KS = sort((Ks(:))); %Ordena de menor a mayor
xx = xx + 1;
end
%Parámetros por Máxima Verosimilitud
parmhat = wblfit(Ks);
AlfaMV = parmhat (1,1);
BetaMV = parmhat (1,2);
[M,V] = wblstat(AlfaMV,BetaMV);
AlfaMV % Parámetro con MV
BetaMV % Parámetro con MV
M; % Media
V; %Varianza
mediaa=M;
handles.M=mediaa;
guidata (hObject,handles);
alfaa=AlfaMV;
handles.alfaa=alfaa;
guidata (hObject,handles);
betaa=BetaMV;
handles.betaa=betaa;
guidata (hObject,handles);
handles.Ks=Ks;
guidata (hObject,handles);
set(handles.alfa,'String',AlfaMV);
set(handles.beta,'String',BetaMV);
set(handles.media,'String',M);
134
set(handles.varianza,'String',V);
KS = sort((Ks(:))); %Ordena de menor a mayor
n = 1;
FTW=zeros(i,1);
FCUM=zeros(i,1);
FTWEXP=zeros(i,1);
FCUMEXP=zeros(i,1);
kaese=KS;
handles.KS=kaese;
guidata (hObject,handles);
while n<=i,
t = (KS(n,1));
Ftw = ((BetaMV*(t^(BetaMV-1)))/(AlfaMV^BetaMV))*(exp((t/AlfaMV)^(BetaMV)));
FTW(n,1)=Ftw;
Fcum = (1 - (exp(-(t/AlfaMV)^(BetaMV))));
FCUM(n,1) = Fcum;
Conf = (exp(-(t/AlfaMV)^(BetaMV)));
CONF(n,1) = Conf;
n = n+1;
end
cdf=FCUM;
handles.FCUM=cdf;
guidata (hObject,handles);
confiabilidad=CONF;
handles.CONF=confiabilidad;
guidata (hObject,handles);
%--------------------------------------------------------------------%Grafica PDF e histograma
ttt=0.5:1:max(KS);
ff=hist(KS,ttt);
h=ff / sum(ff);
tt=linspace(0,max(KS),100);
f2=@(tt) (BetaMV/AlfaMV)*((tt/AlfaMV).^(BetaMV-1)).*exp((tt/AlfaMV).^BetaMV);
%Grafica PDF
axes(handles.graf);
cla reset;
x=min(KS):0.1:max(KS);
f = wblpdf(x,AlfaMV,BetaMV);
bar(ttt,h); hold on
135
plot(x,f,'r');
plot(tt,f2(tt),'r');
hold off
set(handles.graf, 'xgrid', 'on', 'ygrid', 'on');
%--------------------------------------------------------------------%Puebas de Bondad
%tratamiento de datos
Numeric1 = handles.archivo;
Numeric2 = sort(Numeric1);
ii2 = size (Numeric1,1);
iii2=1;
n2=1;
Datosfrec=zeros(n2,2);
Datosfrec (n2,1) = n2;
if iii2==1,
Datosfrec (n2,2) = Numeric2 (iii2,2);
iii2=iii2+1;
n2=n2+1;
Datosfrec (n2,1) = n2;
end;
while iii2<=ii2,
if Numeric2 (iii2,2) == Numeric2 (iii2-1,2);
else
Datosfrec (n2,2) = Numeric2 (iii2,2);
Datosfrec (n2,1) = n2;
n2=n2+1;
end;
iii2=iii2+1;
end;
Datosfrec1=Datosfrec(:,2);
pd = fitdist(Datosfrec1,'Weibull');
% según seleccion nivel de sensibilidad
Nivel=handles.nivel;
if Nivel==0.05,
NS=0.05;
else
if Nivel==0.01,
NS=0.01;
else
if Nivel==0.05,
NS=0.05;
else
if Nivel==0.1,
NS=0.1;
136
else
if Nivel==0.2,
NS=0.2;
end;
end;
end;
end;
end;
%Kolmogorov-Smirnov
kolmogorov = kstest(Datosfrec1,'CDF',pd,'Alpha',NS)
if kolmogorov==0,
'La Hipótesis se acepta'
else
'La Hipótesis se rechaza'
end;
set(handles.hipo1,'String',ans);
% Chi-Cuadrado
chicuadradoo = chi2gof(Datosfrec1,'CDF',pd,'Alpha',NS)
if chicuadradoo==0,
'La Hipótesis se acepta'
else
'La Hipótesis se rechaza'
end;
set(handles.hipo2,'String',ans);
end;
%--------------------------------------------------------------------%---------------------------------------------------------------------
%recuadro cálculos
%opciones
function uipanel9_SelectionChangeFcn(hObject, eventdata, handles)
if hObject == handles.conf
op=1;
handles.op=op;
guidata (hObject,handles);
elseif hObject == handles.probf
op=2;
%(V>v)
%(V<v)
137
handles.op=op;
guidata (hObject,handles);
elseif hObject == handles.tasa
op=3;
handles.op=op;
guidata (hObject,handles);
%(potencia media disponible)
end;
%botón calcular
function calculos_Callback(hObject, eventdata, handles)
opcion= handles.op;
AlfaMV=handles.alfaa;
BetaMV=handles.betaa;
KS=handles.KS;
M=mean(KS);
if opcion==1,
get(handles.dato,'String');
num = str2double(get(handles.dato,'String'));
t=num;
Conf = (exp(-(t/AlfaMV)^(BetaMV)));
set(handles.resultado,'String',Conf);
end;
if opcion==2,
get(handles.dato,'String');
num = str2double(get(handles.dato,'String'));
t=num;
Fcum = (1 - (exp(-(t/AlfaMV)^(BetaMV))));
set(handles.resultado,'String',Fcum);
end;
if opcion==3,
%potencia media
potenciam=0.5*1.225*M^3*gamma(1+3/BetaMV)/(gamma(1+1/BetaMV)^3);
set(handles.resultado,'String',potenciam);
end;
%--------------------------------------------------------------------%---------------------------------------------------------------------
%Cálculo potencia aerogenerador
%botón cargar datos generador
function pushbutton6_Callback(hObject, eventdata, handles)
[FileName Path]=uigetfile({'*.xlsx'},'Abrir Documento');
handles.datosgenerador = xlsread(fullfile(Path, FileName));
guidata(hObject, handles);
%botón calcular
function pushbutton7_Callback(hObject, eventdata, handles)
138
potencia=handles.datosgenerador;
AlfaMV=handles.alfaa;
BetaMV=handles.betaa;
i = size(potencia,1);
x = (potencia(1,1));
Ks = zeros(i,1);
xx=1;
while xx <= i,
y = (potencia(xx,2));
Ks(xx,1)= y;
KS = sort((Ks(:))); %Ordena de menor a mayor
xx = xx + 1;
end
KS;
Pr=max(KS);
get(handles.v0,'String');
v0 = str2double(get(handles.v0,'String'));
get(handles.vr,'String');
vr = str2double(get(handles.vr,'String'));
get(handles.v1,'String');
v1 = str2double(get(handles.v1,'String'));
x0=v0;
xr=vr;
x1=v1;
x=min(KS):0.5:x1;
pot=KS(x>=x0 & x<=xr);
axes(handles.graf);
cla reset;
hold on
x=x0:0.5:xr;
plot(x,pot,'ro','markersize',2,'markerfacecolor','r');
axis([0 15 -10 1550]);
grid on
p=polyfit(x,pot',3); %ajuste a un polinomio de tercer grado
yp=polyval(p,x);
plot(x,yp,'k');
hold off
%cálculo de la potencia media aerogenerador
f=@(x) (BetaMV/AlfaMV)*((x/AlfaMV).^(BetaMV-1)).*exp((x/AlfaMV).^BetaMV); %función de Weibull
h=@(x) f(x).*polyval(p,x);
power=quad(h,x0,xr)+Pr*quad(f,xr,x1);
set(handles.potenciag,'String',power);
%---------------------------------------------------------------------
139
%--------------------------------------------------------------------%menú desplegable gráficas
function graficos_Callback(hObject, eventdata, handles)
valor_graficos=get(handles.graficos,'Value');
AlfaMV=handles.alfaa;
BetaMV=handles.betaa;
KS=handles.KS;
FCUM=handles.FCUM;
CONF=handles.CONF;
i=handles.i;
n = 1;
P=zeros(i,1);
tt=linspace(0,max(KS),100);
f2=@(tt) (BetaMV/AlfaMV)*((tt/AlfaMV).^(BetaMV-1)).*exp((tt/AlfaMV).^BetaMV);
switch valor_graficos
case 1
%Grafica PDF
tt=linspace(0,max(KS),100);
f2=@(tt) (BetaMV/AlfaMV)*((tt/AlfaMV).^(BetaMV-1)).*
exp(-(tt/AlfaMV).^BetaMV);
axes(handles.graf);
cla reset;
x=min(KS):0.1:max(KS);
f = wblpdf(x,AlfaMV,BetaMV);
hold on
plot(x,f,'r');
plot(tt,f2(tt),'r')
hold off
set(handles.graf, 'xgrid', 'on', 'ygrid', 'on');
case 2
%Grafica CDF
axes(handles.graf)
cla reset;
hold on
x=min(KS):1:max(KS);
f = wblcdf(x,AlfaMV,BetaMV); %linea
plot(x,f);
plot(KS,FCUM,'x');
%puntos
hold off
set(handles.graf, 'xgrid', 'on', 'ygrid', 'on');
case 3
%Grafica CDF complemetaria
axes(handles.graf)
cla reset;
hold on
plot(min(KS):1:max(KS),1cdf('wbl',min(KS):1:max(KS),AlfaMV,BetaMV)); %linea
140
plot(KS,CONF,'x');
%puntos
hold off
set(handles.graf, 'xgrid', 'on', 'ygrid', 'on');
case 4
cla reset;
potencia=cp;
x=0:0.5:25; %velocidad
hold on
plot(x, potencia,'b')
ylim([-10 1550])
xlabel('velocidad')
ylabel('potencia')
grid on
hold off
end;
%--------------------------------------------------------------------%---------------------------------------------------------------------
141
Anexo 5
Tabla y curva de potencia aerogenerador Acciona AW 70-1500 Class I entregadas por el
fabricante.
Wind Speed m/s
Power Output kw
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
6.5
7
7.5
8
8.5
9
9.5
10
10.5
11
11.5
12
12.5
13
13.5
14
14.5
15
15.5
16
16.5
17
0
0
0
0
0
0
0
10
45
78
119
167
220
284
358
442
538
633
737
836
942
1,061.00
1,163.00
1,272.00
1,358.00
1,419.00
1,461.00
1,489.00
1,500.00
1,500.00
1,500.00
1,500.00
1,500.00
1,500.00
1,500.00
142
17.5
18
18.5
19
19.5
20
20.5
21
21.5
22
22.5
23
23.5
24
24.5
24.99
1,500.00
1,500.00
1,500.00
1,500.00
1,500.00
1,500.00
1,500.00
1,500.00
1,500.00
1,500.00
1,500.00
1,500.00
1,500.00
1,500.00
1,500.00
1,500.00