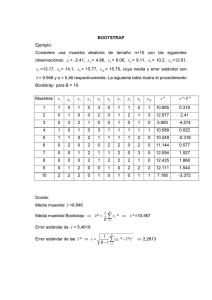
Universidad de Granada Bootstrap en poblaciones finitas
Anuncio

Universidad de Granada
Departamento de Estadı́stica e Investigación Operativa
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
Máster Oficial en Estadı́stica Aplicada
Granada, julio de 2014
Índice general
1. EL MÉTODO BOOTSTRAP
4
1.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
1.2. Estimación bootstrap de la distribución del estimador de un parámetro de interés
6
1.3. Estimación bootstrap del error estándar . . . . . . . . . . . . . . . . . . . . . .
7
1.4. Estimación bootstrap del sesgo . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
1.5. Intervalos de confianza bootstrap: Métodos de construcción . . . . . . . . . . . .
8
1.5.1. Intervalo de confianza bootstrap Normal estándar . . . . . . . . . . . . .
8
1.5.2. Intervalo de confianza bootstrap percentil . . . . . . . . . . . . . . . . .
9
1.5.3. Intervalo de confianza bootstrap básico . . . . . . . . . . . . . . . . . . . 10
1.5.4. Intervalo de confianza bootstrap t (estudentizado) . . . . . . . . . . . . . 11
1.5.5. Intervalo de confianza bootstrap mejorado, BCa . . . . . . . . . . . . . . 12
2. BOOTSTRAP EN POBLACIONES FINITAS
15
2.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2.2. Muestreo aleatorio simple con reemplazamiento . . . . . . . . . . . . . . . . . . 17
2.3. Muestreo aleatorio simple sin reemplazamiento . . . . . . . . . . . . . . . . . . . 19
2.3.1. Variante del factor de corrección (F) . . . . . . . . . . . . . . . . . . . . 21
2.3.2. Variante del reescalado (R)
. . . . . . . . . . . . . . . . . . . . . . . . . 21
2.3.3. Variante BWR (Replacement bootstrap) . . . . . . . . . . . . . . . . . . 22
2.3.4. Variante BWO . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
2.3.5. Variante Mirror-Match (MM) . . . . . . . . . . . . . . . . . . . . . . . . 25
2
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
2.4. Muestreo con probabilidades proporcionales al tamaño muestral con reemplazamiento . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
2.5. Muestreo con probabilidades proporcionales al tamaño muestral sin reemplazamiento . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
2.6. Muestreo estratificado . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
2.6.1. Muestreo aleatorio simple con y sin reemplazamiento en los estratos . . . 34
2.6.2. Muestreo con probabilidades proporcionales al tamaño muestral con reemplazamiento en los estratos . . . . . . . . . . . . . . . . . . . . . . . . 36
2.6.3. Muestreo con probabilidades proporcionales al tamaño muestral sin reemplazamiento en los estratos . . . . . . . . . . . . . . . . . . . . . . . . 38
2.7. Muestreo multietápico con estratificación . . . . . . . . . . . . . . . . . . . . . . 40
2.7.1. Muestreo con probabilidades proporcionales al tamaño muestral con reemplazamiento en la primera etapa . . . . . . . . . . . . . . . . . . . . . 40
2.7.2. Muestreo πps en la primera etapa . . . . . . . . . . . . . . . . . . . . . . 43
2.8. Estimadores no lineales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
3. Aplicaciones con R
52
3.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
3.2. Muestreo aleatorio simple con reemplazamiento . . . . . . . . . . . . . . . . . . 52
3.3. Muestreo aleatorio simple sin reemplazamiento . . . . . . . . . . . . . . . . . . . 60
A. Funciones implementadas
67
B. Diseños muestrales y estimadores usuales
72
3
Capı́tulo
1
EL MÉTODO BOOTSTRAP
1.1.
Introducción
El bootstrap fue introducido en 1979 por Bradley Efron, aunque experimentó avances en
años sucesivos gracias a aportaciones de otros autores como Robert Tibshirani, Michael Chernick, Jun Shao o Anthony Davison.
Los métodos bootstrap son una clase de métodos Monte Carlo no paramétricos que
pretenden estimar la distribución de una población mediante remuestreo. Los métodos de
remuestreo tratan una muestra observada como una población finita, y generan muestras
aleatorias a partir de ella para estimar caracterı́sticas poblacionales y hacer inferencia sobre la
población muestreada. A menudo estos métodos se usan cuando no se conoce la distribución
de la población objetivo, de modo que la muestra es la única información disponible.
El término bootstrap puede referirse a bootstrap no paramétrico o bootstrap paramétrico. Los métodos de Monte Carlo que implican el muestreo a partir de una distribución
de probabilidad completamente especificada, son conocidos como bootstrap paramétrico. En el
caso no paramétrico la distribución no se especifica.
4
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
La distribución de la población finita representada por la muestra puede ser vista como
una pseudopoblación con caracterı́sticas similares a las de la verdadera población. Generando
repetidamente muestras aleatorias de esta pseudopoblación (remuestreo), se puede estimar la
distribución muestral de un estadı́stico. El remuestreo permite también estimar propiedades de
un estimador tales como su sesgo o su error estándar.
Cabe señalar que las estimaciones bootstrap de una distribución de muestreo son análogas
a la idea de estimación de la densidad. El histograma de una muestra proporciona una estimación de la forma de la función de densidad. El histograma no es la densidad, pero desde el
punto de vista no paramétrico puede ser visto como una estimación razonable de la misma.
Existen métodos para generar muestras aleatorias de densidades completamente especificadas;
el bootstrap genera muestras aleatorias a partir de la distribución empı́rica de la muestra.
Supongamos que x = {x1 , . . . , xn } es una muestra aleatoria observada de una distribución
con función de distribución F (x). Si a partir de x se selecciona aleatoriamente X ∗ , entonces
P [X ∗ = xi ] =
1
, i = 1, . . . , n
n
El remuestreo genera una muestra aleatoria X1∗ , . . . , Xn∗ mediante el muestreo con reemplazamiento de x. Las variables aleatorias Xi∗ son independientes e idénticamente distribuidas de
manera uniforme en el conjunto de {x1 , . . . , xn }.
La función de distribución empı́rica, Fn (x), es un estimador de F (x). Puede probarse que
Fn (x) es un estadı́stico suficiente de F (x); es decir, toda la información sobre F (x) contenida
en la muestra está también contenida en Fn (x). Aún más, Fn (x) es en sı́ misma la función de
distribución de una variable aleatoria, a saber, la variable aleatoria que se distribuye de manera
uniforme en el conjunto x = {x1 , . . . , xn }. Por tanto, la función de distribución empı́rica Fn es la
función de distribución de X ∗ . Ası́, en bootstrap, pueden considerarse dos aproximaciones. Por
una parte, Fn es una aproximación de FX ; y, por otra, la función de distribución empı́rica Fm∗ de
5
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
las réplicas bootstrap es una aproximación de Fn . El remuestreo a partir de x equivale a generar
muestras aleatorias de la distribución Fn (x). Las dos aproximaciones pueden ser representadas
mediante el diagrama
F → X → Fn
Fn → X ∗ → Fn∗
Para generar una muestra aleatoria bootstrap mediante remuestreo de x, basta generar n
números enteros aleatorios {i1 , . . . , in } uniformemente distribuidos en 1, . . . , n y seleccionar la
muestra bootstrap x∗ = {xi1 , . . . , xin }.
1.2.
Estimación bootstrap de la distribución del estimador de un parámetro de interés
Sea θ un parámetro poblacional de interés (que puede ser un vector) y θ̂ un estimador de
θ. Entonces, la estimación bootstrap de la distribución de θ̂ se obtiene como sigue:
1. Para cada réplica bootstrap, indexada por b = 1, . . . , B:
a) Generar la muestra x∗(b) = {x∗1 , . . . , x∗n } mediante muestreo con reemplazamiento a
partir de la muestra observada {x1 , . . . , xn }
b) Calcular la réplica b−ésima de θ̂(b) a partir de la b−ésima muestra bootstrap.
2. La estimación bootstrap de Fθ̂ (·) es la distribución empı́rica de las réplicas θ̂(1) , . . . , θ̂(B) .
6
Bootstrap en poblaciones finitas
1.3.
Samuel Nicolás Gil Abreu
Estimación bootstrap del error estándar
La estimación bootstrap del error estándar de un estimador θ̂ es la desviación estándar
muestral de las réplicas bootstrap θ̂(1) , . . . , θ̂(B) , dada por
σ
bθ̂∗
v
u
u
=t
B
1 X (b)
(θ̂ − θ̂∗ )2
B − 1 b=1
donde
θ̂∗
B
1 X (b)
=
θ̂ .
B b=1
Según Efron y Tibshirani, el número de réplicas necesarias para obtener una buena estimación del error estándar no es elevado; por lo general B = 50 es suficiente, y con escasa
frecuencia se precisa B > 200. En cambio, sı́ es necesario que B sea mucho mayor para la
estimación mediante intervalos de confianza.
1.4.
Estimación bootstrap del sesgo
Si θ̂ es un estimador insesgado de θ, entonces E[θ̂] = θ. En general el sesgo de un estimador
θ̂ de θ está dado por
sesgo[θ̂] = E[θ̂ − θ] = E[θ̂] − θ .
Ası́, cada estadı́stico es un estimador insesgado de su valor esperado y, en particular, la media
muestral de una muestra aleatoria es un estimador insesgado de la media de la distribución.
La estimación bootstrap del sesgo utiliza las réplicas bootstrap de θ̂ para estimar la disb Para una población finita x = (x1 , . . . , xn ), el parámetro es θ̂(x) y
tribución muestral de θ.
disponemos de B estimadores independientes e idénticamente distribuidos, θ̂(b) . Dado que la
media muestral de las réplicas {θ̂(b) } es insesgada para su valor esperado E[θ̂∗ ], la estimación
7
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
bootstrap del sesgo es:
s\
esgo[θ̂] = θ̂∗ − θ̂
siendo θ̂∗ =
1
B
PB
b=1
θ̂(b) y θ̂ = θ̂(x) la estimación obtenida a partir de la muestra observada x.
Cabe señalar que en bootstrap se muestrea Fn en lugar de FX , luego θ se reemplazará por
θ̂ a la hora de estimar el sesgo. Además, un sesgo positivo indicará que θ̂ tiende a sobreestimar
en media a θ, y un sesgo negativo indicará que θ̂ subestima a dicho parámetro.
1.5.
Intervalos de confianza bootstrap: Métodos de construcción
En esta sección vamos a presentar diversas aproximaciones para construir intervalos de
confianza bootstrap para un parámetro de interés.
1.5.1.
Intervalo de confianza bootstrap Normal estándar
Esta aproximación es la más simple, aunque no necesariamente la mejor. Sea θ̂ un estimador
del parámetro θ con error estándar σθ̂ . Si θ̂ es una media muestral y el tamaño muestral es
grande, entonces por el Teorema Central del Lı́mite se tiene que
Z=
θ̂ − E[θ̂]
σθ̂
se aproxima a una Normal estándar.
Por consiguiente, si θ̂ es insesgado para θ, resulta de forma aproximada que
θ̂ ± zα/2 · σθ̂
8
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
donde zα/2 = Φ−1 (1− α2 ), con Φ la función de distribución de la Normal estándar, es un intervalo
de confianza para θ al nivel de confianza 100(1 − α) %.
Este intervalo es fácil de calcular, aunque acabamos de ver que requiere varios supuestos. Por
un lado, θ̂ debe tener distribución normal o ser una media muestral y que el tamaño muestral
sea suficientemente grande; y, por otro, θ̂ debe ser insesgado para θ.
Además, aquı́ σθ̂ se ha tratado como un parámetro conocido, aunque en bootstrap es estimado por la desviación estándar muestral de las réplicas bootstrap de θ̂, lo que proporciona el
intervalo
θ̂ ± zα/2 · σ
bθ̂∗ .
El sesgo puede ser estimado y utilizado para centrar el estadı́stico Z, lo que da lugar al
intervalo corregido por el sesgo
θ̂ ± zα/2 · σ
bθ̂∗ − (θ̂∗ − θ̂) = (2θ̂ − θ̂∗ ) ± zα/2 · σ
bθ̂∗ ,
que está centrado en (2θ̂ − θ̂∗ ).
1.5.2.
Intervalo de confianza bootstrap percentil
Utiliza la distribución empı́rica de las réplicas bootstrap como distribución de referencia. Los
cuantiles de la distribución empı́rica son estimadores de los cuantiles de la distribución muestral
de θ̂, con lo que estos cuantiles aleatorios reproducirán mejor la verdadera distribución cuando
la distribución de θ̂ no sea Normal.
Supóngase que θ̂(1) , . . . , θ̂(B) son las réplicas bootstrap del estadı́stico θ̂. A partir de la
función de distribución de las réplicas se calculan los cuantiles de órdenes
respectivamente, que definen el intervalo de confianza.
9
α
2
y 1 − α2 , θ̂ α2 y θ̂1− α2 ,
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
Efron y Tibshirani probaron que el intervalo Percentil presenta ventajas teóricas sobre el
intervalo normal estándar y un mejor comportamiento en la práctica.
1.5.3.
Intervalo de confianza bootstrap básico
Este intervalo transforma la distribución de las réplicas bootstrap restando el estadı́stico
observado. Los cuantiles de la muestra transformada se usan para determinar los lı́mites de
confianza.
Considérese T un estimador de θ, y sea kα el cuantil de orden α de T − θ. Entonces:
P [T − θ > kα ] = 1 − α ⇒ P [T − kα > θ] = 1 − α
Ası́, un intervalo de confianza al nivel de confianza 100 · (1 − 2α) % con el mismo error α en
la cola inferior y superior, está dado por (t − k1−α , t − kα ).
En bootstrap, la distribución de T es habitualmente desconocida, pero los cuantiles pueden
ser estimados.
Sea θ̂α el cuantil de orden α calculado a partir de la función de distribución empı́rica de las
réplicas θ̂∗ . Y sea bα el cuantil de orden α de θ̂∗ − θ̂. Entonces b̂α = θ̂α − θ̂ es un estimador de
bα .
Por tanto, un lı́mite de confianza superior aproximado para un nivel de confianza del 100(1−
α) % está dado por
θ̂ − b̂α/2 = θ̂ − (θ̂α/2 − θ̂) = 2θ̂ − θ̂α/2 .
De un modo similar un lı́mite inferior de confianza aproximado está dado por
2θ̂ − θ̂1−α/2 .
10
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
Ası́, el intervalo de confianza bootstrap básico al nivel de confianza del 100(1 − α) % es
(2θ̂ − θ̂1−α/2 , 2θ̂ − θ̂α/2 )
1.5.4.
Intervalo de confianza bootstrap t (estudentizado)
θ̂ − E[θ̂]
no
σθ̂
sigue exactamente una distribución normal, dado que σθ̂ es estimada. Tampoco puede afirmarse
Incluso si θ̂ tiene distribución normal y θ̂ es insesgado para θ, el estadı́stico Z =
que se trate de un estadı́stico t de Student puesto que se desconoce la distribución del estimador
bootstrap σ
bθ̂ .
El intervalo de confianza bootstrap t, o estudentizado, no utiliza la distribución t de Student
como distribución de referencia, sino que genera mediante remuestreo la distribución muestral
de un estadı́stico de “tipo t”.
Sea x = (x1 , . . . , xn ) la muestra aleatoria observada. Se obtiene el correspondiente estadı́stico
observado θ̂. El intervalo de confianza bootstrap t al nivel de confianza 100(1 − α) % es
(θ̂ − t∗1−α/2 · σ
bθ̂ , θ̂ − t∗α/2 · σ
bθ̂ )
donde σ
bθ̂ , t∗1−α/2 y t∗α/2 se calculan como sigue:
1. Calcular θ̂ = θ̂(x).
2. Para cada réplica bootstrap, indexada por b = 1, . . . , B:
(b)
(b)
a) Generar la b-ésima muestra bootstrap x(b) = (x1 , . . . , xn ) mediante muestreo con
reemplazamiento a partir de x
b) Calcular θ̂(b) a partir de la b-ésima muestra bootstrap x(b) .
c) Calcular o estimar el error estándar σ
bθ̂(b) remuestreando a partir de x(b) , no de x, de
forma independiente para cada muestra bootstrap.
11
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
d ) Obtener la b-ésima réplica del estadı́stico “t”,
t(b) =
θ̂(b) − θ̂
σ
bθ̂(b)
3. Obtener los cuantiles muestrales t∗α/2 y t∗1−α/2 de la muestra ordenada de réplicas t(b) , dado
que la muestra de réplicas t(1) , . . . , t(B) es la distribución de referencia para “t”.
4. Calcular σ
bθ̂ como la desviación estándar muestral de las réplicas θ̂(b) .
5. Determinar los lı́mites de confianza θ̂ − t∗1−α/2 · σ
bθ̂ y θ̂ − t∗α/2 · σ
bθ̂ .
La desventaja de este tipo de intervalos reside en que la estimación de los errores estándar
σ
bθ̂(b) debe obtenerse mediante bootstrap. Ası́, si B = 1000, el tiempo empleado en calcular el
intervalo de confianza bootstrap t es aproximadamente 1000 veces mayor que el empleado en
aplicar cualquiera de los otros métodos.
1.5.5.
Intervalo de confianza bootstrap mejorado, BCa
Los intervalos de confianza bootstrap mejorados son una variante de los intervalos percentil
que poseen mejores propiedades teóricas y proporcionan un rendimiento superior en la práctica.
Para un nivel de confianza 100 · (1 − α) %, los habituales cuantiles de órdenes α/2 y 1 − α/2
son ajustados por dos factores: una corrección para el sesgo, y otra para la asimetrı́a o ajuste
de aceleración.
El intervalo de confianza bootstrap mejorado, que notamos BCa, está dado por
(θ̂α∗ 1 , θ̂α∗ 2 ) ,
donde los lı́mites de confianza están dados por los cuantiles muestrales de órdenes
12
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
α1 = Φ ẑ0 +
ẑ0 + zα/2
1 − â(ẑ0 + zα/2 )
y
α2 = Φ ẑ0 +
ẑ0 + z1−α/2
1 − â(ẑ0 + z1−α/2 )
de las réplicas bootstrap, donde
zα = Φ−1 (α) ,
B
1 X
I(θ̂(b) < θ̂)
B b=1
ẑ0 = Φ−1
!
y
Pn
i=1 (θ()
â =
6·
Pn
i=1
q
− θ(i) )3
((θ() − θ(i) )2 )3/2
con I la función indicadora.
El factor de corrección del sesgo, ẑ0 , es en realidad una estimación de una medida del sesgo
mediano de las réplicas θ̂∗ de θ̂. Si θ̂ es la mediana de las réplicas bootstrap, entonces ẑ0 = 0.
El factor de aceleración, â, es una estimación de una medida de la asimetrı́a a partir de las
réplicas jackknife.
Cabe señalar que existen otros métodos para estimar la aceleración. El factor de aceleración â
debe su nombre a que estima la tasa de cambio del error estándar de θ̂ con respecto al parámetro
θ (en una escala normalizada). Al usar el intervalo de confianza bootstrap normal estándar se
supone que θ̂ es aproximadamente Normal con esperanza θ y varianza σ(2θ̂) independiente del
parámetro θ. Sin embargo, no siempre es cierto que la varianza de un estimador sea constante
con respecto al parámetro. El factor de aceleración tiene como objetivo ajustar los lı́mites
de confianza para tener en cuenta la posibilidad de que la varianza de los estimadores pueda
depender del verdadero valor del parámetro a estimar.
Los intervalos de confianza bootstrap BCa tienen dos importantes ventajas teóricas:
13
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
Son “invariantes” frente a transformaciones en el parámetro, es decir, si (θ̂α∗ 1 ; θ̂α∗ 2 ) es un
intervalo de confianza de este tipo para θ, y t(θ) es una transformación del parámetro θ,
entonces
t(θ̂α∗ 1 ), t(θ̂α∗ 2 )
es el intervalo correspondiente para t(θ).
Tienen precisión de segundo orden, esto es, su error tiende a 0 a la velocidad 1/n.
El intervalo de confianza bootstrap t tiene precisión de segundo orden, pero no es respetado
por las transformaciones. El intervalo de confianza bootstrap percentil sı́ es respetado por las
transformaciones, pero tiene precisión de primer orden (su error tiende a cero a la velocidad
p
1/ (n)). Y el intervalo de confianza bootstrap Normal no posee ninguna de estas propiedades.
14
Capı́tulo
2
BOOTSTRAP EN POBLACIONES FINITAS
2.1.
Introducción
En este capı́tulo vamos a tratar el problema de estimación de la varianza en el muestreo en
poblaciones finitas mediante el método bootstrap.
Como sabemos el método bootstrap es un método de replicación. Otros métodos de replin
cación son: el método de los grupos aleatorios, basado en réplicas de tamaño ; el método de
k
n
las semimuestras, que emplea réplicas de tamaño ; y el método jackknife, que trabaja con
2
réplicas de tamaño n − j. En comparación con los métodos anteriores, el método bootstrap
utiliza réplicas de cualquier tamaño n∗ .
Sea Y1 , . . . , Yn una muestra de una variables aleatorias independientes e idénticamente distribuidas con función de distribución F . Sea θ un parámetro desconocido de la distribución
que se desea estimar. Notaremos θb al estimador muestral de θ. En lo sucesivo trataremos el
b V ar[θ],
b muestreando repetidamente.
problema de estimar la varianza de θ,
Una muestra bootstrap es una muestra aleatoria simple con reemplazamiento de tamaño n∗
seleccionada a partir de una muestra inicial, que es considerada como una pseudopoblación
para este muestreo. Notaremos Y1∗ , . . . , Yn∗ a las observaciones bootstrap.
15
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
Sea θb∗ el estimador bootstrap de θ, que tiene la misma forma funcional que θb pero aplicado
a la muestra bootstrap en lugar de a la muestra de partida. Entonces, el estimador bootstrap
b está definido por
de V ar[θ]
b = V ar∗ [θb∗ ]
v1 [θ]
donde V ar∗ denota la varianza condicionada dada la muestra inicial o pseudopoblación.
El muestreo bootstrap repetido a partir de la muestra de partida genera muestras alternativas que podrı́an haber sido seleccionadas como muestra de partida de F . Ası́, la idea de
este método es emplear la varianza en el muestreo bootstrap repetido para estimar la varianza,
b
V ar[θ].
b Sin
En casos sencillos en los que θb es lineal es posible determinar la expresión de v1 [θ].
embargo, en general, no se tiene la expresión exacta y es preciso recurrir a una aproximación.
Dicho método de aproximación consta de tres pasos:
1. Generar un número grande, A, de muestras bootstrap independientes a partir de la muestra inicial.
2. Para cada muestra bootstrap calcular el correspondiente estimador θbα∗ , α = 1, . . . , A, del
parámetro de interés.
3. Determinar la varianza muestral de los valores θbα∗ , α = 1, . . . , A; esto es:
A
b =
v2 [θ]
1 X b∗ b∗ 2
θ −θ
A − 1 α=1 α
con:
A
∗
1 X b∗
b
θ =
θ
A α=1 α
Claramente v2 converge a v1 cuando A → ∞. Efron y Tybshirani (1986) comentan que un
valor de A entre 50 y 200 es adecuado en muchas situaciones.
16
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
La aproximación v2 de v1 es fácil de calcular en todos los casos. En lo que sigue vamos a
estudiar el estimador bootstrap para diseños muestrales sencillos y estimadores lineales, para
los que se dispone de resultados exactos. El método bootstrap funciona bien en estos casos, en
los que los estimadores habituales de la varianza también están disponibles, y este adecuado
comportamiento motiva su uso en diseños más complicados, para los que no disponemos de
los estimadores habituales de la varianza. Finalmente se considerarán diseños más complejos y
estimadores no lineales.
2.2.
Muestreo aleatorio simple con reemplazamiento
Supóngase que se desea estimar la media poblacional Y de una variable y en estudio en una
población finita U de tamaño N . Se seleccionan n unidades en la población mediante muestreo
aleatorio simple con reemplazamiento. Sean y1 , . . . , yn los valores muestrales de y. Entonces, es
habitual estimar Y mediante la media muestral; esto es:
y=
1X
yi
n
Es sabido que la varianza de este estimador y el estimador usual de la varianza vienen dados,
respectivamente, por:
V ar[y] =
σ2
n
y
v[y] =
s2
n
siendo:
N
1 X
σ =
(Yi − Y )2
N i=1
2
17
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
y
n
1 X
s =
(yi − y)2
n − 1 i=1
2
Además, v[y] es un estimador insesgado de V ar[y].
En este caso, la muestra bootstrap y1∗ , . . . , yn∗ ∗ es una m.a.s. con reemplazamiento de tamaño
n∗ obtenida a partir de la muestra inicial de tamaño n, y el correspondiente estimador para la
media poblacional es la media muestral
y∗ =
1 X ∗
yi
n∗
1
, i = 1, . . . , n, entonces la media y
n
la varianza condicionadas de y1∗ , dada la muestra de partida, están dadas por:
Considérese, por ejemplo, y1∗ . Dado que P [y1∗ = yi ] =
n
1X
=
yi = y
n i=1
E∗ [y1∗ ]
y
n
V
ar∗ [y1∗ ]
n−1 2
1X
(yi − y)2 =
·s
=
n i=1
n
respectivamente. Dado que las observaciones bootstrap y1∗ , . . . , yn∗ ∗ son independientes e idénticamente distribuidas por construcción, la media y la varianza condicionadas de y ∗ , dada la
muestra de partida, resultan ser:
n
E∗ [y ∗ ] = E∗ [y1∗ ] =
1X
yi = y
n i=1
y
v1 [y] = V ar∗ [y ∗ ] =
1
n − 1 s2
∗
·
V
ar
[y
]
=
· ∗
∗ 1
n∗
n
n
18
(2.1)
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
respectivamente. Ası́, en general, el estimador bootstrap de la varianza v1 [y] no coincide con el
estimador usual de la varianza v[y] y no es un estimador insesgado de V ar[y]. Esta deseable
propiedad se obtiene si y sólo si n∗ = n − 1.
Teorema 2.1 Dada una muestra aleatoria simple con reemplazamiento de tamaño n de una
población finita de tamaño N , el estimador bootstrap de la varianza, v1 [y], es un estimador
insesgado de V ar[y] si y sólo si el tamaño de la muestra bootstrap es una unidad menos que
el tamaño de la muestra original; es decir, n∗ = n − 1. Para n∗ = n el sesgo de v1 [y] como
estimador de V ar[y] está dado por
sesgo[v1 [y]] = −
1
· V ar[y]
n
Para tamaños muestrales grandes, el sesgo no parece ser relevante, mientras que para tamaños muestrales pequeños podrı́a ser muy importante. Por ejemplo, si n = 2 y n∗ = n el sesgo
serı́a del 50 %.
2.3.
Muestreo aleatorio simple sin reemplazamiento
El método bootstrap no se adecúa con facilidad a los diseños muestrales sin reemplazamiento, incluso en los casos más simples. En esta sección se describen algunas variaciones del método
estándar que pueden ser apropiados para el muestreo aleatorio simple sin reemplazamiento. El
parámetro de interés será la media poblacional Y .
Sea s la muestra de partida de tamaño n y s∗ la muestra bootstrap de tamaño n∗ . En
principio se supondrá que s∗ se ha obtenido a partir de s mediante muestreo aleatorio simple
con reemplazamiento. Más adelante se cambiará este supuesto.
19
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
La media muestral y es el estimador habitual de la media poblacional. Es fácil probar que
para el estimador bootstrap
y∗ =
1 X ∗
yi
n∗
se tiene que:
E∗ [y ∗ ] = E∗ [yi∗ ] =
1X
yi = y
n i∈s
y
V ar∗ [y ∗ ] =
1
1 1 X
n − 1 s2
∗
2
·
· ∗
V
ar
[y
]
=
·
(y
−
y)
=
∗ i
i
n∗
n n∗ i∈s
n
n
Cabe señalar que estos resultados no se ven afectados por el diseño muestral de la muestra
de partida sino únicamente por el diseño de la muestra bootstrap, de modo que coinciden con
los obtenidos en la sección anterior para el muestreo aleatorio simple con reemplazamiento.
Teorema 2.2 Sea y1∗ , . . . , yn∗ ∗ una muestra bootstrap de tamaño n∗ obtenida mediante muestreo
aleatorio simple con reemplazamiento de la muestra de partida s, la cual a su vez es elegida de
la población mediante muestreo aleatorio simple sin reemplazamiento. Entonces, el estimador
bootstrap de V ar[y] está dado por
v1 [y] = V ar∗ [y ∗ ] =
n − 1 s2
· ∗
n
n
(2.2)
Por tanto, para el muestreo aleatorio simple sin reemplazamiento, el estimador v1 [y] de la
varianza
V ar[y] = (1 − f ) ·
S2
n
no coincide con el estimador insesgado usual
v[y] = (1 − f ) ·
20
s2
n
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
Y el sesgo de v1 [y] es
sesgo[v1 [y]] = E[v1 [y]] − V ar[y] =
n − 1 S2
S2
· ∗ − (1 − f ) ·
n
n
n
En el caso particular n∗ = n − 1 se tiene que el estimador bootstrap
v1 [y] =
s2
n
es sesgado, con
S2
S2
S2
− (1 − f ) ·
=f·
sesgo[v1 [y]] =
n
n
n
Si f es pequeño, el sesgo de v1 es despreciable. En lo que sigue presentamos cuatro variantes
del método bootstrap estándar para abordar situaciones en las que f no es pequeño.
2.3.1.
Variante del factor de corrección (F)
Si n∗ = n − 1, un estimador insesgado de la varianza está dado simplemente por
v1F (y) = (1 − f ) · v1 [y]
2.3.2.
Variante del reescalado (R)
Rao y Wu (1988) definieron el estimador bootstrap de la varianza en términos de las observaciones reescaladas
yi]
p
=y+ 1−f ·
r
n∗
· (yi∗ − y)
n−1
La media bootstrap es ahora
∗
n
p
1 X ]
y = ∗
yi = y + 1 − f ·
n i=1
]
21
r
n∗
· (y ∗ − y)
n−1
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
y, en virtud del teorema 2.2, el estimador bootstrap de la varianza es
n∗
1−f 2
· V ar∗ [y ∗ ] =
·s
n−1
n
v1R [y] = V ar∗ [y ] ] = (1 − f ) ·
Nótese que v1R coincide con el estimador usual de la varianza de y en muestreo aleatorio
simple sin reemplazamiento, que es insesgado.
Si se considera n∗ = n, entonces las observaciones reescaladas son
yi]
p
=y+ 1−f ·
r
n
· (yi∗ − y),
n−1
mientras que la elección n∗ = n − 1 proporciona
yi] = y +
2.3.3.
p
1 − f · (yi∗ − y)
Variante BWR (Replacement bootstrap)
El método bootstrap con reemplazamiento, debido a McCarthy y Snowden (1985), pretende
eliminar el sesgo de V ar∗ [y ∗ ] haciendo una elección adecuada del tamaño muestral. Tomando
n∗ =
n−1
1−f
en v1 [y], resulta
v1BW R [y] =
1−f 2
·s ;
n
esto es, el estimador usual insesgado de V ar[y] en muestreo aleatorio simple sin reemplazamiento.
22
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
n−1
no sea un número entero,
1
−f
n−1
∗
0
podemos tomar como tamaño n de la muestra bootstrap n =
, n00 = n0 + 1, o una
1−f
aleatorización entre n0 y n00 , donde [[ ]] denota la función entero mayor. Wolter (1985) prefiere
En la práctica, puesto que es muy probable que el cociente
la primera elección, n∗ = n0 , dado que devuelve un estimador conservador de la varianza y su
sesgo es suficientemente pequeño en muchas ocasiones.
2.3.4.
Variante BWO
Gross (1980) introdujo este método bootstrap sin reemplazamiento en el que la muestra
bootstrap es obtenida por muestreo aleatorio simple sin reemplazamiento. Esto es, tanto la
muestra inicial como la bootstrap tienen en común que se obtienen sin reemplazamiento.
Esta variante supone un importante avance teórico, pero su implementación práctica en
muchos diseños es aparentemente complicada.
El procedimiento se resume en cuatro pasos:
N
y se copia cada elemento de la muestra inicial k veces para crear una nueva
n
N
pseudopoblación Us de tamaño N , cuyos elementos denotamos yj0 j=1 . Exactamente k
1. Se toma k =
de estos valores yj0 coinciden con los yi , ∀ i = 1, . . . , n.
2. Construir la muestra bootstrap s∗ de tamaño n∗ a partir de Us mediante muestreo aleatorio
simple sin reemplazamiento
3. Determinar la media bootstrap:
∗
n
1 X ∗
y = ∗
y
n i=1 i
∗
4. Calcular el estimador bootstrap teórico v1BW O (y) = V ar∗ [y ∗ ] o repetir los tres pasos
anteriores un gran número de veces A y calcular la versión de Monte Carlo:
2
A
X
1
y ∗α − 1
v2BW O [y] =
y ∗α0
A − 1 α=1
A 0
A
X
α =1
23
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
Puesto que s∗ se obtiene mediante muestreo aleatorio simple sin reemplazamiento de Us , la
esperanza y la varianza condicionadas de y ∗ quedan en la forma habitual; esto es:
N
1 X 0
1 X
k X
k
E∗ [y ] =
yj =
kyi =
yi =
ny = y
N j=1
N i∈s
N i∈s
N
∗
y
N
N
X
s∗ 2
1 X 0
1
1
∗
0
∗
∗
V ar∗ [y ] = (1 − f ) · ∗ = (1 − f ) · ∗ ·
·
y0
yj −
n
n N − 1 j=1
N j 0 =1 j
= (1 − f ∗ ) ·
X
1
1
·
k (yi − y)2
·
n∗ N − 1 i∈s
= (1 − f ∗ ) ·
1
N
k
·
·
· (n − 1) · s2
∗
n N −1 N
= (1 − f ∗ ) ·
1
N
1
·
· · (n − 1) · s2
∗
n N −1 n
!2
donde:
f∗ =
n∗
N
y
s2 =
X
1
·
(yi − y)2
n − 1 i∈s
Por tanto, se concluye que, en general, el estimador bootstrap v1BW O [y] = V ar∗ [y ∗ ] ni es
insesgado ni coincide con el estimador usual de la varianza
v[y] = (1 − f ) ·
con f =
n
.
N
24
s2
n
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
Si n∗ = n, entonces:
1−f 2
v1BW O (y) =
·s ·
n
N
n−1
·
N −1
n
y el estimador bootstrap es sesgado por el factor:
C=
N · (n − 1)
n · (N − 1)
Para alcanzar la insesgadez puede redefinirse el estimador bootstrap multiplicándolo por C −1 ,
v1BW O = C −1 · V ar∗ [y ∗ ] ,
o trabajar con los valores reescalados
yi] = y +
√
C · (yi∗ − y)
N
no es en general un número entero. El método puede
n
N
0
00
0
0
modificarse para trabajar con k igual a k =
, k = k + 1, o una aleatorización entre k
n
00
0
0
y k . Siguiendo el paso 1, esta aproximación crea pseudopoblaciones de tamaños N = n · k ,
Otra de las dificultades es que k =
00
00
N = n · k , o una aleatorización entre los dos.
2.3.5.
Variante Mirror-Match (MM)
Este método fue introducido por Sitter (1992a, 1992b) para el caso en que la fracción de
muestreo f se grande (no sea despreciable). Se resume en los cuatro pasos siguientes:
1. Elegir una submuestra o grupo aleatorio de tamaño m ∈ Z, 1 ≤ m < n, de la muestra de
partida s mediante muestreo aleatorio simple sin reemplazamiento.
25
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
2. Repetir el paso anterior k veces, con
n 1−e
·
m 1−f
k=
m
. Ası́, la muestra bootstrap estará formada por los k grupos aleatorios
n
seleccionados y tendrá tamaño n∗ = m · k.
donde e =
3. Determinar la media bootstrap
∗
n
k
k
m
1 X ∗
1 XX ∗ 1 X ∗
y = ∗
y
y =
y =
n i=1 i
k m j=1 r=1 i
k j=1 j
∗
siendo y ∗j la media muestral del j-ésimo grupo aleatorio seleccionado, j = 1, . . . , m.
4. Calcular el estimador bootstrap teórico v1M M (y) = V ar∗ [y ∗ ], o repetir los tres pasos
anteriores un gran número de veces, A, y calcular la versión de Monte Carlo:
2
A
X
1
y ∗α − 1
v2M M [y] =
y ∗α0
A − 1 α=1
A 0
A
X
α =1
El tamaño de la muestra bootstrap,
n∗ = n ·
1−e
,
1−f
difiere del tamaño de la muestra de partida a través de la razón de dos factores de corrección
en poblaciones finitas. La elección m = f · n implica que la fracción de submuestreo e coincide
con la fracción principal de muestreo, f . En este caso, n∗ = n .
Por definición, las medias muestrales y ∗j , j = 1, . . . , m, son variables aleatorias independientes e idénticamente distribuidas con medias y varianzas condicionadas:
E∗ [y ∗j ] = y
26
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
y
V ar∗ [y ∗j ] = (1 − e) ·
s2
m
respectivamente, con
n
s2 =
1 X
(yi − y)2
n − 1 i=1
Por tanto, el estimador bootstrap de la varianza es
v1M M (y) =
1
m 1−f
s2
s2
· V ar∗ [y ∗j ] =
·
· (1 − e) ·
= (1 − f ) ·
k
n 1−e
m
n
que es el estimador usual insesgado de la varianza V ar[y].
En la práctica, puesto que k no es habitualmente un número entero, puede redefinirse k
como
0
k =
00
0
0
n 1−e
·
m 1−f
,
00
k = k + 1, o una aleatorización entre k y k . La primera elección devuelve un estimador
conservador de la varianza.
2.4.
Muestreo con probabilidades proporcionales al tamaño muestral con reemplazamiento
Otro caso sencillo surge cuando se selecciona la muestra mediante muestreo con probabilidades proporcionales al tamaño muestral con reemplazamiento. Supóngase ahora que se
desea estimar el total poblacional, Y , de una variable y, y que se dispone de los valores Xi ,
i = 1, . . . , n, de una variable auxiliar X en toda la población. Para formar la muestra se hace
uso de una medida del tamaño de Xi y de n valores aleatorios independientes rk , k = 1, . . . , n,
de una distribución U (0, 1).
27
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
Para el k-ésimo número aleatorio rk , se selecciona la única unidad i para la que Si−1 < rk ≤
Si , donde las sumas acumuladas están definidas por:
Si =
i
X
p i0
i = 1, . . . , N
0
i =1
0
i=0
y
pi =
Xi
X
Sea yk el valor de la variable y para la unidad aleatoriamente seleccionada a partir de rk , e
Irk ∈(Si−1 ,Si ] la variable indicadora
Irk ∈(Si−1 ,Si ] =
1 si rk ∈ (Si−1 , Si ]
0 en otro caso
Entonces, el estimador insesgado estándar para el total poblacional está dado por
n
N
n
n
1 X yk
1 XX
Yi
1X
Yb =
=
Irk ∈(Si−1 ,Si ] ·
=
zk
n k=1 pk
n k=1 i=1
pi
n k=1
con
zk =
N
X
Irk ∈(Si−1 ,Si ] ·
i=1
Yi
pi
Sea ahora r1∗ , . . . , rn∗ ∗ una muestra bootstrap obtenida de la pseudopoblación, r1 , . . . , rn ,
mediante muestreo aleatorio simple con reemplazamiento. El estimador de Y a partir de la
muestra bootstrap es
∗
n
N
1 XX
Yi
Irk∗ ∈(Si−1 ,Si ]
Y = ∗
n k=1 i=1
pi
b∗
28
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
Obsérvese que Yb ∗ es la media de n∗ variables aleatorias independientes e idénticamente
distribuidas
zk =
N
X
Irk∗ ∈(Si−1 ,Si ] ·
i=1
Yi
,
pi
con media y varianza condicionadas:
n
E∗ [z1∗ ] =
1X
zk = Yb
n k=1
y
n
V ar∗ [z1∗ ] =
2
1 X
zk − Yb ,
n k=1
respectivamente.
En consecuencia,
E∗ [Yb ∗ ] = E∗ [z1∗ ] = Yb
y
n
V ar∗ [Yb ∗ ] =
2
1 1 X
1
∗
b
·
V
ar
[z
]
=
z
−
Y
∗
k
1
n∗
n∗ n k=1
(2.3)
"
=
1
n−1 1
·
∗
n
n n−1
n
X
#
(zk − Yb )2
k=1
n−1
Ası́, el estimador bootstrap de la varianza de Yb es v1 [Yb ] = V ar∗ [Yb ∗ ], que resulta ser
n∗
veces el estimador usual de la varianza bajo muestreo con probabilidades proporcionales al
tamaño muestral con reemplazamiento. Si se construye una muestra bootstrap de tamaño n∗ =
n − 1, entonces v1 [Yb ] coincide con dicho estimador y es insesgado. Por otra parte, si n∗ = n, v1
es sesgado, aunque el sesgo es despreciable si n es grande.
29
Bootstrap en poblaciones finitas
2.5.
Samuel Nicolás Gil Abreu
Muestreo con probabilidades proporcionales al tamaño muestral sin reemplazamiento
Otro diseño muestral básico es el muestreo πps o muestreo con probabilidades proporcionales al tamaño muestral sin reemplazamiento, en el que las probabilidades de inclusión son
proporcionales al tamaño de una variable auxiliar. Si Xi es la medida del tamaño para la i−ésima unidad, entonces la probabilidad de inclusión de primer orden para una muestra de tamaño
fijo n es:
πi = n · p i = X i ·
X
n
−1
Las probabilidades de inclusión de segundo orden, que notaremos πij , vienen determinadas por
el algoritmo especı́fico de muestreo con probabilidades proporcionales utilizado.
En lo que sigue nos ocuparemos de la estimación del total poblacional, Y . El estimador de
Horvitz-Thompson habitual es
Yb =
X yi X
1X
=
wi · yi =
ui
πi
n i∈s
i∈s
i∈s
donde ui = n · wi · yi y los pesos wi son los inversos de las probabilidades de inclusión.
Nuestro objetivo es estimar la varianza de Yb utilizando un procedimiento bootstrap. En
este caso, el estimador usual (Yates-Grundy) de V ar[Yb ], es
v[Yb ] =
2
n X
n
X
yi
yj
πi πj − πij
·
−
π
π
πj
ij
i
i=1 j>i
Desafortunadamente, el método bootstrap encuentra grandes dificultades para hacer frente
a este tipo de diseños muestrales. En realidad, ninguna variante bootstrap proporciona un estimador insesgado de la varianza y suele recurrirse a una aproximación bien conocida, a saber,
tratar la muestra como si hubiera sido seleccionada mediante muestreo con probabilidades pro-
30
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
porcionales al tamaño muestral con reemplazamiento. Ası́, sea u∗1 , . . . , u∗n∗ la muestra bootstrap
obtenida mediante muestreo aleatorio simple con reemplazamientoa partir de la muestra de
partida s. Entonces, el estimador bootstrap del total es
∗
n
1 X ∗
∗
b
Y = ∗
u
n i=1 i
donde u∗i = (n · wi · yi )∗ son variables aleatorias independientes e idénticamente distribuidas
tales que
n
E∗ [u∗1 ]
1X
=
ui = Yb
n i=1
y
n
n
X
1X
V ar∗ [u∗1 ] =
(ui − Yb )2 = n
n i=1
i=1
ui Yb
−
n
n
!2
=n
n
X
Yb
wi · yi −
n
i=1
!2
La definición de u∗i pretender preservar en la muestra bootstrap la relación entre wi e yi en la
muestra de partida.
Puesto que la varianza condicionada de Yb ∗ depende únicamente del diseño de la muestra bootstrap, y no del diseño de la muestra inicial, resulta
n
n X
Yb
1
∗
∗
b
wi · yi −
V ar∗ [Y ] = ∗ V ar∗ [u1 ] = ∗
n
n i=1
n
!2
,
(2.4)
que es el estimador bootstrap v1 [Yb ] de la varianza bajo muestreo con probabilidades proporcionales al tamaño muestral sin reemplazamiento.
Si se considera n∗ = n − 1 queda:
n X
Yb
wi · yi −
v1 [Yb ] =
n − 1 i∈s
n
!2
n
n
1 XX
=
n − 1 i=1 j>i
yi
yj
−
π i πj
2
que es el estimador usual insesgado de la varianza en muestreo con probabilidades proporcionales
al tamaño muestral con reemplazamiento.
31
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
v1 [Yb ] es un estimador sesgado de la varianza en muestreo con probabilidades proporcionales
al tamaño muestral sin reemplazamiento y para n∗ = n − 1 se tiene que
sesgo[v1 [Yb ]] =
n
b
b
· V ar[Ywr ] − V ar[Y ]
n−1
donde V ar[Ybwr ] es la varianza del total estimado en muestreo con probabilidades proporcionales
al tamaño muestral con reemplazamiento.
Ası́, el método bootstrap tiende a sobreestimar la varianza en muestreo con probabilidades proporcionales al tamaño muestral sin reemplazamiento siempre que la varianza sea menor
que la varianza en muestreo con probabilidades proporcionales al tamaño muestral con reemplazamiento. El sesgo es probablemente pequeño siempre que n y N sean ambos grandes. En
n
≥ 1.
muestras pequeñas la sobreestimación está agravada por el factor
n−1
Cuando n = 2, la sobreestimación de la varianza puede controlarse mediante reescalado. En
efecto, considerando los valores reescalados
u]i
= Yb +
π1 π2 − π12
π12
12
(u∗i − Yb )
el estimador bootstrap del total es
∗
n
1 X ]
Y = ∗
u
n i=1 i
b]
y el estimador bootstrap de la varianza está dado por
v1R (Yb ) = V ar∗ [Yb ] ] =
1
1 π1 π2 − π12
V ar∗ [u]1 ] = ∗
V ar∗ [u∗1 ]
∗
n
n
π12
Entonces, para n = 2 y n∗ = n − 1 resulta
π1 π2 − π12
v1R (Yb ) =
(w1 y1 − w2 y2 )2 ,
π12
32
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
que coincide con el estimador usual insesgado de Yates-Grundy de la varianza. No obstante, el
reescalado sólo funciona cuando π1 π2 > π12 .
Desafortunadamente no está claro como extender esta variante del reescalado al caso de un
n cualquiera. Alternativamente, cuando n∗ = n − 1, se puede intentar corregir el sesgo de forma
aproximada introduciendo un factor de corrección en la forma
n X
Yb
wi · yi −
v1F [Yb ] = (1 − f ) V ar∗ [Yb ∗ ] = (1 − f )
n − 1 i∈s
n
!2
,
donde
n
1X
πi .
f=
n i=1
Aunque esta corrección no ha sido aceptada por todos, proporciona una sencilla regla práctica
para reducir la sobreestimación de la varianza.
2.6.
Muestreo estratificado
La extensión del método bootstrap a diseños muestrales estratificados es relativamente directa. En primer lugar ha de tenerse en cuenta que las muestras bootstrap deben conformar
una muestra estratificada seleccionada de la muestra de partida. En lo que sigue, este método
se aplicará en los casos de muestreo aleatorio simple con reemplazamiento, muestreo aleatorio
simple sin reemplazamiento, muestreo con probabilidades proporcionales al tamaño muestral
con reemplazamiento y muestreo con probabilidades proporcionales al tamaño muestral sin reemplazamiento, dentro de los estratos. Los detalles de aplicación del bootstrap a estos diseños
muestrales ya han sido presentados en las secciones anteriores.
33
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
Supóngase que la población se divide en L estratos. Sea Nh el número de unidades de la
población que conforma el estrato h-ésimo, h = 1, . . . , L. El muestreo se lleva a cabo de forma
independiente en los diferentes estratos, y nh denota el tamaño muestral en el estrato h-ésimo.
Sean yhi , i = 1, . . . , nh , las observaciones muestrales en el estrato h-ésimo, h = 1, . . . , L. Y
∗
sea yhi
, i = 1, . . . , n∗h , la muestra bootstrap en el estrato h-ésimo, h = 1, . . . , L.
En lo sucesivo, para simplificar, se considerará nh ≥ 2 y n∗h = nh − 1 en todos los estratos;
esto es, el tamaño de las muestras bootstrap es una unidad menos que el tamaño de las muestras
iniciales en cada estrato. Además se supone que las muestras bootstrap se obtienen de forma
independiente en cada estrato mediante muestreo aleatorio simple con reemplazamiento a partir
de la muestra inicial.
2.6.1.
Muestreo aleatorio simple con y sin reemplazamiento en los
estratos
En los casos de muestreo aleatorio simple con reemplazamiento y muestreo aleatorio simple
sin reemplazamiento, el estimador estándar para el total poblacional es:
L
X
Yb =
Ybh
h=1
donde
n
h
Nh X
·
yhi ,
Ybh =
nh i=1
y su versión bootstrap es:
Yb ∗ =
L
X
Ybh∗
h=1
donde
∗
nh
Nh X
∗
b
Yh = ∗ ·
y ∗ = Nh y ∗h ,
nh i=1 hi
34
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
con
∗
nh
1 X
∗
yh = ∗ ·
y∗ .
nh i=1 hi
Entonces, el estimador bootstrap para la varianza está dado por:
v1 [Yb ] = V ar∗ [Yb ∗ ] =
L
X
V ar∗ [Ybh∗ ] =
h=1
L
X
Nh2 · V ar∗ [y ∗h ]
h=1
Y, teniendo en cuenta (2.1) y (2.2), se obtiene que
v1 [Yb ] =
L
X
Nh2 ·
h=1
s2h
nh
con
n
s2h
h
1 X
=
(yhi − y h )2 .
nh − 1 i
Obsérvese que se trata del estimador usual insesgado para la varianza en el caso de muestreo
aleatorio simple con reemplazamiento.
Sin embargo, v1 [Yb ] es sesgado para el muestreo aleatorio simple sin reemplazamiento ya que
nh
omite los factores de corrección para poblaciones finitas. Si las fracciones de muestreo fh =
Nh
son insignificantes en todos los estratos, el sesgo será pequeño y v1 será suficientemente bueno.
En caso contrario, serı́a deseable reducir el sesgo de alguna forma.
La variante del factor de corrección no es factible aquı́ a menos que el tamaño muestral sea
asignado proporcionalmente a los estratos, en cuyo caso
1 − fh = 1 − f
para todos los estratos y
v1F [Yb ] = (1 − f ) · V ar∗ [Yb ∗ ]
35
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
vuelve a ser el estimador usual insesgado de la varianza.
La variante del reescalado también puede utilizarse para reducir el sesgo. A partir de las
observaciones bootstrap reescaladas
1
]
∗
= y h + (1 − fh ) 2 (yhi
− yh) ,
yhi
la versión bootstrap del total poblacional es
Yb ] =
L
X
Ybh]
h=1
donde
∗
nh
X
N
h
]
Ybh = ∗ ·
y] ,
nh i=1 hi
y el correspondiente estimador bootstrap de la varianza está dado por
v1R [Yb ] = V ar∗ [Yb ] ] =
L
X
Nh2 · (1 − fh ) ·
h=1
s2h
,
nh
que reproduce el estimador usual insesgado de la varianza en el muestreo aleatorio simple sin
reemplazamiento.
2.6.2.
Muestreo con probabilidades proporcionales al tamaño muestral con reemplazamiento en los estratos
Si en los estratos se utiliza muestreo con probabilidades proporcionales al tamaño muestral
con reemplazamiento, el estimador del total poblacional es:
Yb =
L
X
h=1
36
Ybh
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
donde
nh
1 X
b
Yh =
zhi
nh i=1
con
zhi =
yhi
.
phi
Su versión bootstrap es
Yb ∗ =
L
X
Ybh∗
h=1
donde
nh
1 X
∗
∗
b
zhi
Yh = ∗
nh i=1
con
∗
zhi
=
yhi
phi
∗
.
Y el estimador bootstrap de la varianza está dado por
v1 [Yb ] = V ar∗ [Yb ∗ ] =
L
X
V ar∗ [Ybh∗ ]
h=1
Entonces, por (2.3), resulta que
v1 [Yb ] =
L
X
h=1
n
h 2
X
1
zhi − Ybh
nh · (nh − 1) i=1
que es el estimador usual insesgado de la varianza.
37
Bootstrap en poblaciones finitas
2.6.3.
Samuel Nicolás Gil Abreu
Muestreo con probabilidades proporcionales al tamaño muestral sin reemplazamiento en los estratos
Finalmente, si en los estratos se usa muestreo con probabilidades proporcionales al tamaño
muestral sin reemplazamiento, el estimador de Horvitz-Thompson del total poblacional es
L
X
Yb =
Ybh
h=1
donde
nh
X
1
uhi
Ybh =
nh i=1
con
uhi = nh · whi · yhi
y
whi =
1
.
πhi
Su versión bootstrap es
Yb ∗ =
L
X
Ybh∗
h=1
donde
∗
Ybh∗
nh
1 X
= ∗
u∗hi
nh i=1
con
u∗hi = (nh · whi · yhi )∗ .
Adoptando la aproximación de tratar la muestra como si hubiera sido seleccionada mediate muestreo con probabilidades proporcionales al tamaño muestral con reemplazamiento y
38
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
teniendo en cuenta (2.4), el estimador bootstrap de la varianza es
v1 [Yb ] = V ar∗ [Yb ∗ ] =
L
X
V ar∗ [Ybh∗ ] =
h=1
L
X
h=1
nh
nh − 1
nh
X
i=1
Ybh
whi · yhi −
nh
!2
Nótese que este estimador es sesgado para muestreo con probabilidades proporcionales al tamaño muestral sin reemplazamiento y, de hecho, sobreestima V ar[Yb ] en la medida en que la
auténtica varianza sea menor que la obtenida en muestreo con probabilidades proporcionales
al tamaño muestral con reemplazamiento.
En determinadas aplicaciones nh = 2, ∀ h = 1, . . . , L. En estos casos el sesgo en la estimación
de la varianza puede eliminarse trabajando con las observaciones reescaladas
u]hi
= Ybh +
πh1 πh2 − πh12
πh12
12
(u∗hi − Ybh )
Entonces, el estimador bootstrap del total es
Yb ] =
L
X
Ybh]
h=1
donde
∗
Ybh]
nh
1 X
= ∗
u]hi .
nh i=1
Y el estimador bootstrap de la varianza está dado por
v1R (Yb ) =
L
X
h=1
V ar∗ [Ybh] ] =
L
X
πh1 πh2 − πh12
πh12
h=1
39
(wh1 yh1 − wh2 yh2 )2 .
Bootstrap en poblaciones finitas
2.7.
Samuel Nicolás Gil Abreu
Muestreo multietápico con estratificación
En esta sección vamos a abordar la estimación bootstrap de la varianza en muestreo estratificado cuando en cada estrato se lleva a cabo un muestreo en dos o más etapas.
En la primera etapa, en cada estrato, haremos uso del muestreo con probabilidades proporcionales al tamaño muestral, con o sin reemplazamiento, para seleccionar una muestra de
conglomerados o unidades primarias de muestreo (PSU). Posteriormente, dentro de cada unidad primaria en cada estrato, se lleva a cabo submuestreo en varias etapas hasta seleccionar en
la última etapa las unidades últimas de muestreo (USU).
El muestreo se supone independiente de un estrato a otro, y el submuestreo dentro de cada
unidad primaria ha de ser independiente del efectuado en las demás.
El método del conglomerado último, introducido por Hansen, Hurwitz y Madow (1953),
permite obtener el estimador de la varianza del estimador del parámetro de interés considerando
el muestreo multietápico como un caso especial de muestreo por conglomerados con una sola
etapa.
Se denomina conglomerado último al conjunto de todas las unidades muestrales de última
etapa que pertenecen a la misma unidad primaria, independientemente de que se realicen una o
varias etapas de muestreo dentro de cada unidad primaria. La consideración del conglomerado
último simplifica considerablemente la estimación de la varianza porque no es necesario calcular
las componentes de la varianza atribuibles a las demás etapas de muestreo dentro de las PSU.
2.7.1.
Muestreo con probabilidades proporcionales al tamaño muestral con reemplazamiento en la primera etapa
Consideremos L estratos y supongamos que en cada estrato se seleccionan nh , h = 1, . . . , L,
conglomerados o PSUs mediante muestreo con probabilidades proporcionales al tamaño mues-
40
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
tral con reemplazamiento siendo phi la probabilidad que tiene la i-ésima PSU de ser seleccionada
P h
en cada extracción ( ni=1
phi = 1) en el h-ésimo estrato.
Supongamos que estamos interesados en estimar el total poblacional, Y . Sea Yhi el total
poblacional dentro de la i-ésima PSU en el estrato h-ésimo, esto es, dentro de la (h, i)−ésima
PSU. Y sea Ybhi el estimador de Yhi en el conglomerado ultimo de la i-ésima unidad PSU en el
estrato h-ésimo.
La forma de Ybhi no es importante. Sin embargo, Ybhi deberı́a ser un buen estimador de
Yhi , lo que significa que deberı́a ser insesgado o aproximadamente insesgado. Además, deberı́a
emplearse el mismo estimador (con la misma forma funcional) para cada PSU dentro de un
estrato.
El total poblacional puede estimarse mediante
Yb =
L
X
Ybh
h=1
donde
nh
nh
1 X
Ybhi
1 X
=
zhi
Ybh =
nh i=1 phi
nh i=1
con
zhi =
Ybhi
.
phi
Asumiendo muestreo con probabilidades proporcionales al tamaño muestral con reemplazamiento, es conocido que el estimador usual insesgado de la varianza V ar[Yb ] es
v[Yb ] =
L
X
h=1
v[Ybh ] =
L
X
h=1
n
h 2
X
1
b
zhi − Yh
nh · (nh − 1) i=1
41
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
Para llevar a cabo la estimación bootstrap, la muestra bootstrap puede construirse mediante
el siguiente procedimiento:
1. Seleccionar una muestra de n∗1 PSUs a partir de la muestra inicial (pseudopoblación) en
el primer estrato mediante muestreo aleatorio simple con reemplazamiento.
2. De manera independiente, tomar una muestra de n∗2 PSUs a partir de la muestra inicial
en el segundo estrato mediante muestreo aleatorio simple con reemplazamiento.
3. Repetir el paso 2 para los restantes estratos, h = 3, . . . , L.
4. Aplicar el método de los conglomerados últimos. Esto significa que cuando una PSU
es seleccionado en la muestra bootstrap, todas las unidades del conglomerado último
son incluidas en la muestra bootstrap. Ası́, la muestra bootstrap conforma una muestra
multietápica, estratificada, de la población. Su diseño es similar al de la muestra de
partida.
La versión bootstrap de Yb es
Yb ∗ =
L
X
Ybh∗
h=1
donde
∗
Ybh∗
∗
nh
nh
1 X
Ybhi∗
1 X
= ∗
= ∗
z∗
nh i=1 phi
nh i=1 hi
con Ybhi∗ la versión bootstrap de Ybhi en el conglomerado ultimo de la i-ésima unidad PSU en el
estrato h-ésimo, y
∗
zhi
=
Ybhi∗
.
phi
∗
En el h-ésimo estrato, las variables zhi
, i = 1, . . . , n∗h , tienen esperanza y varianza condicio-
nadas comunes dadas por:
∗
E∗ [zhi
]
nh
1 X
=
zhi = Ybh
nh i=1
42
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
y
V
∗
]
ar∗ [zhi
nh 2
1 X
=
zhi − Ybh .
nh i=1
Ası́, podemos dar el siguiente teorema:
Teorema 2.3 El estimador bootstrap ideal de la varianza está dado por
v1 [Yb ] =
L
X
V ar∗ [Ybh∗ ] =
h=1
nh L
L
2
∗
X
V ar∗ [zh1
] X 1 1 X
b
zhi − Yh
=
·
·
n∗h
n∗ nh i=1
h=1 h
h=1
Obsérvese que el estimador bootstrap coincide con el estimador usual insesgado de la varianza
cuando n∗h = nh − 1.
Para otros tamaños de la muestra bootstrap, tales como n∗h = nh , se tiene que v1 es sesgado
de V ar[Yb ]. El sesgo puede ser relevante para tamaños pequeños de nh .
2.7.2.
Muestreo πps en la primera etapa
En lo que sigue vamos a centrar nuestra atención en el muestreo multietápico cuando las
nh PSUs son seleccionadas mediante algún esquema πps en cada estrato.
Sea Nh el número de PSUs en el estrato h-ésimo, y supongamos que la probabilidad de
seleccionar la i-ésima PSU en el estrato h-ésimo es
πhi = nh phi ,
con 0 < πhi < 1,
PNh
i
phi = 1 y phi proporcional al valor Xi de alguna variable auxiliar x.
Sea Yhi el total poblacional en la (h, i)-ésima PSU. Vamos a considerar un estimador del
total poblacional Y de la forma
Yb =
L
X
h=1
43
Ybh
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
donde
Ybh =
nh
X
Ybhi
i=1
πhi
nh
1 X
Ybhi
=
nh i=1 phi
con Ybhi un estimador de Yhi resultado del submuestreo en la segunda y sucesivas etapas.
Si Yhi = E(Ybhi | i), la varianza de Yb está dada por
V ar[Yb ] =
L
X
V ar(Ybh ) =
h=1
L
X
"
V ar
nh
X
Yhi
i=1
h=1
πhi
#
+
Nh
X
σ2
!
2hi
i=1
πhi
2
donde σ2hi
= V ar(Ybhi | i) es la contribución a la varianza debida al muestreo en la segunda y
sucesivas etapas dentro de la (h, i)-ésima PSU.
El estimador Yb de este tipo más utilizado es
Yb =
L
X
Ybh =
nh X
L X
X
whij · yhij
h=1 i=1 j∈shi
h=1
donde shi es el conjunto de USUs observadas resultado del submuestreo en la segunda y sucesivas
etapas dentro de la (h, i)−ésima PSU, y whij es el peso asociado a la (h, i, j)−ésima USU.
Yb puede escribirse como
Yb =
nh
L
X
1 X
uhi.
nh i=1
h=1
donde
uhi. =
X
uhij ,
j∈shi
con
uhij = nh · whij · yhij
44
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
La versión bootstrap de Yb es
Yb ∗ =
L
X
Ybh∗ =
nh X
L X
X
∗
whij
· yhij
h=1 i=1 j∈shi
h=1
donde los pesos bootstrap están dados por
∗
whij
= thi ·
nh
· whij
n∗h
siendo thi el número de veces que la (h, i)-ésima PSU es seleccionado en la muestra bootstrap.
thi puede tomar los valores 0, 1, . . . , n∗hi . Para las PSUs no seleccionadas, thi = 0 y los corres∗
= 0. Para las PSUs seleccionadas pero no
pondientes pesos bootstrap son también nulos, whij
duplicadas en la muestra bootstrap se tiene que thi = 1 y los pesos bootstrap
∗
whij
=
nh
· whij
n∗h
reflejan el producto del peso de la (h, i)-ésima PSU en la muestra inicial y el inverso de la fracción
de muestreo bootstrap. Para las PSUs seleccionados y duplicadas en la muestra bootstrap se
tiene que thi ≥ 2 y los pesos bootstrap reflejan el producto del peso de la (h, i)-ésima PSU en
la muestra inicial, el inverso de la fracción de muestreo bootstrap, y el número de veces que la
PSU ha sido seleccionada.
Yb ∗ también puede escribirse en la forma
∗
nh
L
X
1 X
∗
b
Y =
u∗hi.
∗
n
h=1 h i=1
con
!∗
u∗hi. =
X
nh · whij · yhij
j∈shi
la versión bootstrap de uhi. para i = 1, . . . , n∗h , h = 1, . . . , L.
45
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
Las variables u∗hi. son independientes e idénticamente distribuidas con varianza condicionada
V
ar∗ [u∗h1. ]
nh 2
1 X
b
uhi. − Yh
=
nh i=1
Entonces, el estimador bootstrap de la varianza resulta ser ahora
v1 [Yb ] = V ar∗ [Yb ∗ ] =
L
X
V ar∗ [Ybh∗ ] =
h=1
=
nh
L
X
nh X
X
n∗h
j∈shi
h=1
i=1
whij · yhij
L
X
V ar∗ [u∗h1. ]
n∗h
h=1
Ybh
−
nh
!2
Para n∗h = nh − 1, puede probarse que la esperanza del estimador bootstrap es
E[v1 [Yb ]] =
L
X
E nh
nh − 1
h=1
nh
X
i=1
Yhi.
πhi
nh
1 X
Yhi0 .
−
nh i0 =1 πhi0
!2
+
Nh
X
σ2
2hi
i=1
πhi
Comparando esta expresión con la varianza de Yb concluimos que el estimador bootstrap incluye
de forma adecuada las contribuciones a la varianza del submuestreo dentro de cada PSU.
2.8.
Estimadores no lineales
En esta sección vamos a considerar la estimación bootstrap de la varianza para estimadores
no lineales.
Una cuestión clave es porqué cabrı́a esperar que el método bootstrap proporcione un estimador de la varianza razonablemente bueno para un estimador no lineal. Hemos visto que el
método bootstrap funciona bien para estimadores lineales, ya que tiene la capacidad de reproducir el estimador usual insesgado de la varianza. Una adecuada elección de n∗ y el método
46
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
del reescalado proporcionan la insesgadez. Puesto que el método funciona con estadı́sticos lineales, deberı́a funcionar también con estadı́sticos no lineales dado que localmente poseen un
comportamiento lineal.
Sea T un vector de dimensión p × 1 de totales poblacionales, y sea θ un parámetro general
de interés en una población finita, definido por
θ = g(T ) ,
donde g es continuamente diferenciable.
Si Tb es un estimador insesgado de T obtenido a partir de una muestra s determinada por
algún esquema general de muestreo, entonces el estimador de θ es
θ̂ = g(Tb)
El método bootstrap para estimar V ar(θ̂) se concreta en los siguientes pasos:
1. Obtener una muestra bootstrap s∗1 por los métodos vistos en las secciones anteriores.
2. Determinar T̂1∗ , la versión bootstrap de los totales estimados basada en la muestra bootstrap.
3. Calcular la versión bootstrap del estimador θ̂1∗ = g(T̂1∗ )
4. Si es posible, determinar el estimador bootstrap ideal de la varianza, v1 [θ̂] = V ar∗ [θ̂1∗ ],
finalizando de este modo el procedimiento de estimación bootstrap. En caso contrario,
continuar con los siguientes pasos y emplear el método de Monte Carlo para aproximar
el estimador ideal bootstrap.
5. Tomar A − 1 muestras bootstrap más, s∗α , lo que da un total de A muestras. Las muestras
deben ser mutuamente independientes.
47
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
6. Determinar T̂α∗ , las versiones bootstrap de los totales estimados para α = 1, . . . , A.
7. Calcular las versiones bootstrap del estimador θ̂α∗ = g(T̂α∗ ) para α = 1, . . . , A.
8. Finalmente, calcular el estimador bootstrap de Monte Carlo de la varianza:
A 2
X
1
v2 [θ̂] =
·
θ̂α∗ − θ̄ˆ∗
A − 1 α=1
con:
A
1 X ∗
θ̂
θ̄ˆ∗ = ·
A α=1 α
Como alternativa conservadora se puede calcular v2 en términos de las diferencias al cuadrado respecto de θ̂ en lugar de θ̄ˆ∗ .
A continuación vamos a mostrar, a modo de ejemplo, cómo puede aplicarse el método al
importante problema del estimador de razón.
Supondremos que se ha entrevistado a una muestra multietápica seleccionada dentro de L
estratos, obteniéndose ası́ observaciones yhij , xhij para la j−ésima unidad última de muestreo
(USU) seleccionada dentro de la i−ésima unidad primaria de muestreo (PSU) obtenida en el
h−ésimo estrato. Los estimadores usuales de los totales poblacionales son:
Yb =
nh X
mhi
L X
X
whij · yhij
h=1 i=1 j=1
y
b=
X
nh X
mhi
L X
X
whij · xhij
h=1 i=1 j=1
donde nh es el número de PSUs seleccionados dentro del estrato h-ésimo, mhi es el número de
USUs entrevistadas dentro de la (h, i)-ésimo PSU, y whij es el peso asignado a la (h, i, j)−ésima
USU. Dichos pesos reflejan los inversos de las probabilidades de inclusión y quizás otros factores,
48
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
b sean estimadores insesgados o casi insesgados de los
y son especificados de modo que Yb y X
correspondientes totales poblacionales Y y X.
A menudo resulta de interés en la investigación en encuestas la razón de los totales
θ = Y /X ,
que se estima habitualmente por
b.
θ̂ = Yb /X
Para estimar V ar(θ̂) debemos obtener de forma independiente A muestras bootstrap como
se indicó en la sección 2.7, y para cada una de ellas, α = 1, . . . , A, calcular las versiones
bootstrap de los totales poblacionales:
Ybα∗ =
nh X
mhi
L X
X
wαhij · yhij
h=1 i=1 j=1
y
b∗ =
X
α
nh X
mhi
L X
X
wαhij · xhij
h=1 i=1 j=1
donde los pesos bootstrap están dados por
wαhij = tαhi ·
nh
· whij
n∗h
siendo tαhi el número de veces que la (h, i)-ésima PSU de la muestra inicial es seleccionada
dentro de la α-ésima muestra bootstrap.
Entonces calcularemos las versiones bootstrap de la razón
b∗
θ̂α∗ = Ybα∗ /X
α
49
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
para α = 1, . . . , A.
Finalmente, evaluaremos el estimador bootstrap de Monte Carlo de la varianza
A 2
X
1
∗
∗
ˆ
·
θ̂ − θ̄
v2 [θ̂] =
A − 1 α=1 α
Otro importante parámetro de interés en la investigación en encuestas está definido como
la solución de la ecuación:
N
X
[Yi − µ(Xi θ)]Xi = 0
i=1
Si se considera una variable dependiente y dicotómica y
exθ
,
µ(xθ) =
1 + exθ
el parámetro θ se corresponde con aquél que define el modelo de regresión simple logı́stica;
mientras que para una variable dependiente y cualquiera y
µ(xθ) = xθ ,
el parámetro θ se corresponde con la pendiente en el modelo de regresión lineal simple sin
término constante.
Dado el plan de muestreo multietápico con estratificación considerado anteriormente, el
estimador θ̂ está definido como la solución de la ecuación
nh X
mhi
L X
X
ˆ · xhij = 0
whij · [yhij − µ(xhij θ)]
h=1 i=1 j=1
50
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
El estimador θ̂ puede ser obtenido mediante el método iterativo de Newton-Raphson:
θ̂
(k+1)
= θ̂
(k)
+
" L n m
h X
hi
XX
#−1
0
whij · µ (xhij θ̂
(k)
)·
x2hij
h=1 i=1 j=1
·
nh X
mhi
L X
X
whij · [yhij − µ(xhij θ̂(k) )] · xhij
h=1 i=1 j=1
siendo
µ0 (xθ) =
µ(xθ) · [1 − µ(xθ)], para el problema de regresión simple logı́stica
1, para el problema de regresión lineal simple
Para la α-ésima muestra bootstrap, la versión bootstrap θ̂α∗ del estimador θ̂ está definida
como la solución de la ecuación
nh X
mhi
L X
X
wαhij · [yhij − µ(xhij θ̂α∗ )] · xhij = 0
h=1 i=1 j=1
donde los pesos bootstrap wαhij están definidos como se vio anteriormente. θ̂α∗ puede obtenerse
de nuevo mediante el método iterativo de Newton-Raphson. Finalmente, haciendo uso de las A
muestras bootstrap, el estimador bootstrap de la varianza de θ̂ es
v2 [θ̂] =
A 2
X
1
·
θ̂α∗ − θ̄ˆ∗
A − 1 α=1
El método puede extenderse de forma directa al caso multivariante, en el que θ es (p × 1) y
Xi es (1 × p).
51
Capı́tulo
3
Aplicaciones con R
3.1.
Introducción
En este capı́tulo, como aplicación de los métodos estudiados, se presentan varias funciones
implementadas en el entorno de programación estadı́stica R con el propósito de obtener la
estimación bootstrap de Monte Carlo de la varianza del parámetro de interés, ası́ como su
sesgo, en el caso de emplear muestreo aleatorio simple.
También se analizan brevemente las funciones, de utilidad para nuestros propósitos, de la
librerı́a boot de R, en la que podemos encontrar los métodos y conjuntos de datos del libro
”Bootstrap Methods and Their Applications”, de A. C. Davison y D. V. Hinkley (1997).
Además, se desarrollan varios ejemplos con la ayuda de las funciones comentadas.
3.2.
Muestreo aleatorio simple con reemplazamiento
La función BootSRSWR, de elaboración propia, proporciona el estimador bootstrap de Monte Carlo del error estándar de un estadı́stico de interés y del sesgo de dicho estadı́stico, cuando
52
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
se emplea muestreo aleatorio simple con reemplazamiento para construir las muestras bootstrap
a partir de la muestra de partida.
Los argumentos de la función son:
data
Objeto de tipo vector, matrix o dataframe. Si es un vector, cada componente corresponde a una observación univariante de la muestra inicial; en caso contrario, cada fila
corresponde a una observación multivariante de la muestra inicial.
statistic
Función que será aplicada a los datos y devuelve la versión bootstrap del estadı́stico de
interés. Debe tener 2 argumentos: el primero corresponde a los datos originales (data);
y el segundo es un vector de ı́ndices que determinará la muestra bootstrap.
m
Tamaño de las muestras bootstrap que se van a generar
A
Número de muestras bootstrap que se van a generar.
El valor de la función es un objeto de tipo lista con elementos:
t0
t
El valor observado del estadı́stico de interés aplicado a data.
Un vector con las réplicas bootstrap del estadı́stico de interés, resultado de aplicar la
función statistic.
mean
var
sd
La media de las réplicas bootstrap del estadı́stico de interés.
La estimación bootstrap de la varianza del estadı́stico de interés.
La estimación bootstrap del error estándar del estadı́stico de interés.
bias
La estimación bootstrap del sesgo del estadı́stico de interés.
data
El objeto pasado a la función BootSRSWR como argumento data.
st
El estadı́stico pasado a la función BootSRSWR como argumento statistic.
53
Bootstrap en poblaciones finitas
m
Samuel Nicolás Gil Abreu
El escalar pasado a la función BootSRSWR como argumento m.
Además, la función genera un histograma de la distribución de las estimaciones bootstrap del
estadı́stico de interés.
El código de la función se presenta en el Apéndice A.
Por otra parte, el paquete boot proporciona funciones útiles para llevar a cabo la estimación
bootstrap en este caso. En concreto, son de especial interés las funciones boot y boot.ci.
La función boot genera muestras bootstrap de un estadı́stico de interés a partir de unos
datos de partida, y proporciona la estimación bootstrap del error estándar del estadı́stico de
interés y de su sesgo.
A continuación resumimos los argumentos de la función que son de interés para nuestros propósitos:
data
Objeto de tipo vector, matrix o dataframe. Si es un vector, cada componente corresponde a una observación univariante de la muestra inicial; en caso contrario, cada fila
corresponde a una observación multivariante de la muestra inicial.
statistic
Función que será aplicada a los datos y devuelve la versión bootstrap del estadı́stico
de interés. Para el caso de bootstrap no paramétrico statistic debe tener 2 argumentos:
el primero corresponde a los datos originales (data); y el segundo será habitualmente
un vector de ı́ndices que determinará la muestra bootstrap.
R
sim
Número de muestras bootstrap a generar.
Cadena de caracteres que especifica el tipo de simulación requerida. Su valor por
defecto es ordinary, que corresponde al bootstrap no paramétrico.
54
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
El valor de la función es un objeto de clase boot. Se trata de una lista en la que destacamos los
elementos:
t0
t
El valor observado del estadı́stico de interés aplicado a data.
Una matriz cuyas filas corresponden a las réplicas bootstrap del estadı́stico de interés,
resultado de aplicar la función statistic.
statistic
R
data
El estadı́stico pasado a la función boot como argumento statistic.
El escalar pasado a la función boot como argumento R.
El objeto pasado a la función boot como argumento data.
La función boot.ci calcula hasta 5 tipos de intervalos de confianza bootstrap no paramétricos, a saber, normal, básico, t, percentil y BCa. Sus argumentos más relevantes son:
boot.out
Objeto de clase boot resultado de aplicar la función boot a unos datos observados.
conf
Escalar o vector que especifica los niveles de confianza deseados.
type
Vector de cadenas de caracteres especificando el tipo de intervalos de confianza requeridos. Su valor debe ser un subconjunto de entre los valores c(“norm”, “basic”, “stud”,
“perc”, “bca”), o simplemente “all” si se quieren calcular los 5 tipos de intervalos.
El valor de la función es un objeto de tipo boot.ci. Se trata de una lista con elementos:
R
El número de réplicas bootstrap en las que están basados los intervalos.
t0
El valor observado del estadı́stico de interés en la misma escala que los intervalos.
call
normal
La llamada a la función boot.ci.
Matriz de intervalos calculados usando la aproximación normal
55
Bootstrap en poblaciones finitas
basic
Samuel Nicolás Gil Abreu
Intervalos calculados por el método bootstrap básico.
student
Intervalos calculados por el método bootstrap estudentizado.
percent
Intervalos calculados por el método bootstrap del percentil.
bca
Intervalos calculados por el método bootstrap BCa.
Ejemplo 3.1 En la librerı́a bootstrap de R podemos encontrar el conjunto de datos law. Se
trata de un dataframe que contiene las observaciones muestrales de la puntuación media en
las pruebas de admisión, LSAT , y del promedio de calificaciones en grado medio, GP A, en 15
Facultades de Derecho.
> library(bootstrap)
> law
LSAT GPA
1
576 339
2
635 330
3
558 281
4
578 303
5
666 344
6
580 307
7
555 300
8
661 343
9
651 336
10
605 313
11
653 312
12
575 274
13
545 276
14
572 288
15
594 296
56
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
Este conjunto de datos es una muestra aleatoria del conjunto de datos law82 que corresponde
a una población de 82 Facultades de Derecho. Se pretende estimar la correlación entre las
puntuaciones LSAT y GP A, y calcular el error estándar de la estimación bootstrap de la
correlación muestral.
La correlación poblacional y su estimación muestral, a partir de law, están dadas por
> cor(law82$LSAT,law82$GPA)
[1] 0.7599979
> cor(law$LSAT,law$GPA)
[1] 0.7763745
Vamos a hacer uso de la función BootSRSWR especificando muestras bootstrap del mismo tamaño que la muestra inicial. A continuación se muestra el código necesario y la salida
proporcionada por R.
> BootSRSWR(law, function(x,i) cor(x[i,1], x[i,2]), 15, 2000)
Estimaci{\’o}n a partir de la muestra inicial: 0.77637
Media de las estimaciones bootstrap:
0.76913
Estimaci{\’o}n bootstrap de la varianza:
Error est{\’a}ndar:
0.01873
0.13684
Estimaci{\’o}n bootstrap del sesgo:
-0.00725
La Figura 3.1 muestra la distribución de las estimaciones bootstrap obtenidas.
La estimación bootstrap puede obtenerse también haciendo uso de la función boot del paquete boot. El código a ejecutar y la salida obtenida son los siguientes:
> boot.obj <- boot(data=law, statistic=function(x,i) cor(x[i,1], x[i,2]), R
=2000)
> boot.obj
57
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
Distribución de las estimaciones bootstrap
587
440
294
147
0
0.00
0.25
0.50
0.75
1.00
Figura 3.1: Distribución de las estimaciones bootstrap de la correlación lineal entre LSAT y
GP A
ORDINARY NONPARAMETRIC BOOTSTRAP
Call: boot(data = law, statistic = function(x, i) cor(x[i, 1], x[i, 2]), R =
2000)
Bootstrap Statistics :
original
bias
t1* 0.7763745 -0.005824032
std. error
0.1287397
Finalmente vamos a calcular los intervalos de confianza bootstrap para la correlación lineal
entre LSAT y GP A, al nivel de confianza del 95 %, mediante la función boot.ci.
> boot.ci(boot.obj, type="all")
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS Based on 2000 bootstrap replicates
58
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
CALL : boot.ci(boot.out = boot.obj, type = "all")
Intervals : Level
95 %
( 0.5299,
Level
95 %
Normal
1.0345 )
Percentile
( 0.4757,
Basic
( 0.5897,
1.0770 )
BCa
0.9631 )
( 0.3647,
0.9398 )
Calculations and Intervals on Original Scale
Ejemplo 3.2 El conjunto de datos patch del paquete bootstrap contiene medidas de cierta hormona en el caudal sanguı́neo de 8 individuos tras haber llevado tres parches médicos diferentes:
un parche placebo (placebo), un parche antiguo (old) y un parche nuevo (new).
> library(bootstrap)
> patch
subject placebo oldpatch newpatch
z
y
1
1
9243
17649
16449
8406 -1200
2
2
9671
12013
14614
2342
3
3
11792
19979
17274
8187 -2705
4
4
13357
21816
23798
8459
5
5
9055
13850
12560
4795 -1290
6
6
6290
9806
10157
3516
351
7
7
12412
17208
16570
4796
-638
8
8
18806
29044
26325 10238 -2719
2601
1982
Se considera el parámetro de interés θ definido como:
θ=
E[new] − E[old]
E[old] − E[placebo]
59
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
Si |θ| ≤ 0.2 se acepta la bioequivalencia de los parches antiguos y los nuevos; esto es,
se asumirá que a todos los efectos terapeúticos los parches producen el mismo efecto en los
pacientes. El estadı́stico es de la forma Y /Z, con Y = new − old y Z = old − placebo. Vamos a
determinar los estimadores bootstrap de la desviación estándar y del sesgo del estadı́stico razón
de bioequivalencia.
El código necesario, especificando muestras bootstrap del mismo tamaño que la muestra de
partida, y la salida proporcionada por R, se muestran a continuación:
> BootSRSWR(patch[,c("y","z")], function(x,i) mean(x[i,1])/mean(x[i,2]), 8,
2000)
Estimaci{\’o}n a partir de la muestra inicial: -0.07131
Media de las estimaciones bootstrap:
-0.06659
Estimaci{\’o}n bootstrap de la varianza:
Error est{\’a}ndar:
0.01075
0.10368
Estimaci{\’o}n bootstrap del sesgo:
0.00472
La Figura 3.2 muestra la distribución de las estimaciones bootstrap obtenidas.
3.3.
Muestreo aleatorio simple sin reemplazamiento
La función BootSRSWOR, de elaboración propia, proporciona el estimador bootstrap de
Monte Carlo del error estándar de un estadı́stico de interés y del sesgo de dicho estadı́stico,
cuando se emplea muestreo aleatorio simple sin reemplazamiento para construir las muestras
bootstrap a partir de la muestra de partida. La función implementa las variantes BW O y M M .
Los argumentos de la función son:
60
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
Distribución de las estimaciones bootstrap
394
296
197
98
0
−0.30
−0.11
0.07
0.26
0.45
Figura 3.2: Distribución de las estimaciones bootstrap de la razón de bioequivalencia
data
Objeto de tipo vector, matrix o dataframe. Si es un vector, cada componente corresponde a una observación univariante de la muestra inicial; en caso contrario, cada fila
corresponde a una observación multivariante de la muestra inicial.
variante
Cadena de caracteres que especifica las variantes del método bootstrap que se van
a utilizar. Sus valores pueden ser: “BWO”, para la variante BW O; “MM”, para la
variante M M ; u “all”, si se van a utilizar las dos variantes.
statistic
Función que será aplicada a los datos y devuelve la versión bootstrap del estadı́stico de
interés. Debe tener 2 argumentos: el primero corresponde a los datos originales (data);
y el segundo es un vector de ı́ndices que determinará la muestra bootstrap.
N El tamaño de la población de la que se ha extraı́do la muestra inicial
m Vector o escalar, en función de variante. Si variante es “all”, m es un vector que
especifica el tamaño de las muestras bootstrap que se van a generar en la variante
BW O y el número de grupos aleatorios en los que se dividirá la muestra inicial en la
variante M M .
61
Bootstrap en poblaciones finitas
A
Samuel Nicolás Gil Abreu
Número de muestras bootstrap que se van a generar.
El valor de la función es un objeto de tipo lista con elementos:
t0
t
El valor observado del estadı́stico de interés aplicado a data.
Lista con componentes BWO, MM, o ambas, según variante. Cada componente contiene las réplicas bootstrap del estadı́stico de interés, resultado de aplicar la función
statistic, para la correspondiente variante.
mean
El vector de medias de las réplicas bootstrap del estadı́stico de interés para variante.
var
El vector de estimaciones bootstrap de la varianza del estadı́stico de interés para
variante.
sd
El vector de estimaciones bootstrap del error estándar del estadı́stico de interés para
variante.
bias
El vector de estimaciones bootstrap del sesgo del estadı́stico de interés para variante.
data
El objeto pasado a la función BootSRSWOR como argumento data.
st
El estadı́stico pasado a la función BootSRSWOR como argumento statistic.
N El escalar pasado a la función BootSRSWOR como argumento N
m El vector o escalar pasado a la función BootSRSWOR como argumento m.
Además, la función genera histogramas de la distribución de las estimaciones bootstrap del
estadı́stico.
El código de la función se encuentra en el Apéndice A.
62
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
Ejemplo 3.3 A partir de la muestra law del ejemplo 3.2, vamos a obtener las estimaciones
bootstrap de la media poblacional y de la correlación lineal entre ambas variables, mediante
muestreo aleatorio simple sin reemplazamiento BW O y M M .
Utilizaremos la función BootSRSWOR implementada. Para la variante BWO vamos a construir muestras bootstrap del mismo tamaño que la muestra de partida, 15. En el caso de la
variante M M vamos a considerar grupos aleatorios de tamaño 5 de la muestra de partida. A
continuación recogemos el código necesario y las salidas proporcionadas por R:
Medias poblacionales de LSAT y GP A.
La medias poblacionales y su estimaciones muestrales, a partir de law, están dadas por
> sapply(law82[,-1], mean)*c(1,100)
LSAT
GPA
597.5488 313.4878
> sapply(law, mean)
LSAT
GPA
600.2667 309.4667
Las estimaciones bootstrap de la varianza y el sesgo de la medias muestrales de LSAT y
GP A son:
> BootSRSWOR(law$LSAT, "all", function(x,i) mean(x[i]), 82, c(15,5), 2000)
Estimaci{\’o}n a partir de la muestra inicial: 600.2667
Media de las estimaciones bootstrap:
600.26827 (BWO)
Estimaci{\’o}n bootstrap de la varianza:
Error est{\’a}ndar:
9.62597 (BWO)
600.5931 (MM)
92.6593 (BWO)
228.73238 (MM)
15.1239 (MM)
Estimaci{\’o}n bootstrap del sesgo:
0.0016 (BWO)
0.32643 (MM)
> BootSRSWOR(law$GPA, "all", function(x,i) mean(x[i]), 82, c(15,5), 2000)
63
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
Estimaci{\’o}n a partir de la muestra inicial: 309.4667
Media de las estimaciones bootstrap:
309.50737 (BWO)
Estimaci{\’o}n bootstrap de la varianza:
Error est{\’a}ndar:
5.39766 (BWO)
309.3127 (MM)
29.13469 (BWO)
81.1138 (MM)
9.00632 (MM)
Estimaci{\’o}n bootstrap del sesgo:
0.0407 (BWO)
-0.15397 (MM)
Las Figuras 3.3 y 3.4 muestran la distribución de las estimaciones bootstrap obtenidas.
Distribución de las estimaciones bootstrap (BWO)
400
300
200
100
0
565.24
583.87
602.50
621.13
639.76
Distribución de las estimaciones bootstrap (MM)
263
197
132
66
0
560.27
581.39
602.50
623.61
644.73
Figura 3.3: Distribución de las estimaciones bootstrap de la media poblacional de LSAT
64
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
Distribución de las estimaciones bootstrap (BWO)
304
228
152
76
0
294.11
302.55
311.00
319.45
327.89
Distribución de las estimaciones bootstrap (MM)
431
323
216
108
0
280.19
295.10
310.00
324.90
339.81
Figura 3.4: Distribución de las estimaciones bootstrap de la media poblacional de GP A
Correlación lineal entre LSAT y GP A.
> BootSRSWOR(law, "all", function(x,i) cor(x[i,1], x[i,2]), 82, c(15,5),
2000)
Estimaci{\’o}n a partir de la muestra inicial: 0.77637
Media de las estimaciones bootstrap:
0.77171 (BWO)
Estimaci{\’o}n bootstrap de la varianza:
Error est{\’a}ndar:
0.12159 (BWO)
0.01478 (BWO)
0.76072 (MM)
0.05582 (MM)
0.23626 (MM)
Estimaci{\’o}n bootstrap del sesgo:
-0.00466 (BWO)
-0.01565 (MM)
La Figura 3.5 muestra la distribución de las estimaciones bootstrap obtenidas.
65
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
Distribución de las estimaciones bootstrap (BWO)
323
242
162
81
0
0.25
0.44
0.62
0.81
1.00
Distribución de las estimaciones bootstrap (MM)
754
566
377
188
0
−0.30
0.03
0.35
0.67
1.00
Figura 3.5: Distribución de las estimaciones bootstrap de la correlación lineal entre LSAT y
GP A
66
Apéndice
A
Funciones implementadas
BootSRSWR
function (data, statistic, m, A) {
n <- NROW(data)
index <- seq_len(n)
theta0 <- statistic(data, index)
cat("\nEstimaci{\’o}n a partir de la muestra inicial:", round(theta0, digits
=5))
Index.boot <- replicate(A, sample(index, m, replace=TRUE), simplify=FALSE)
theta.boot <- sapply(Index.boot, statistic, x = data)
av <- mean(theta.boot)
cat("\n\nMedia de las estimaciones bootstrap: ", round(av, digits=5))
Var <- var(theta.boot)
cat("\nEstimaci{\’o}n bootstrap de la varianza: ", round(Var, digits=5))
Sd <- sqrt(Var)
cat("\nError est{\’a}ndar: ", round(Sd, digits=5))
67
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
sesgo <- av - theta0
cat("\nEstimaci{\’o}n bootstrap del sesgo: ", round(sesgo, digits=5))
hist(theta.boot, freq=TRUE, main="Distribuci{\’o}n de las estimaciones
bootstrap", axes=FALSE, xlab = "", ylab="", col=terrain.colors(20))
a <- diff(par()$usr[1:2])
axis(1, line = 0.25, at = round(seq(par()$usr[1]+0.04*a, par()$usr[2]-0.04*a
, length.out=5L), digits=2))
axis(2, line = 0.25, at = round(seq(0, par()$usr[4]/1.04, length.out=5L)),
las=1)
cat("\n")
out <- list(t0 = theta0, t = theta.boot, mean = av, var = Var, sd = Sd, bias
= sesgo, data = data, st = statistic, m = m)
invisible(out)
}
BootSRSWOR
function (data, variante="all", statistic, N, m, A) {
n <- NROW(data)
index <- seq_len(n)
theta0 <- statistic(data, index)
cat("\nEstimaci{\’o}n a partir de la muestra inicial:", round(theta0, digits
=5))
theta.boot <- vector("list", 2)
names(theta.boot) <- c("BWO","MM")
68
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
if (is.element(variante, c("BWO", "all"))){
k <- round(N/n)
index.U <- rep(index, each=k)
Index.boot <- replicate(A, sample(index.U, m, replace=FALSE), simplify=
FALSE)
theta.boot$BWO <- sapply(Index.boot, statistic, x = data)
}
if (is.element(variante, c("MM", "all"))){
M <- switch(variante, MM=m[1], all=m[2])
if(M < n){
k <- ceiling(M*(1-M/n)/(M*(1-n/N)))
Index.boot <- replicate(A, unlist(replicate(k, sample(index, M,
replace=FALSE), simplify=FALSE)), simplify=FALSE)
theta.boot$MM <- sapply(Index.boot, statistic, x = data)
}
else cat("No es posible calcular la variante MM (m debe ser menor que n)
")
}
j <- switch(variante, BWO=1L, MM=2L, all=c(1,2))
theta.boot <- theta.boot[j]
av <- structure(sapply(theta.boot, mean), names=c("BWO","MM")[j])
cat("\n\nMedia de las estimaciones bootstrap: ", paste(round(av, digits=5),
" (", names(av), ")", sep="", collapse="
"))
Var <- structure(sapply(theta.boot, var), names=c("BWO","MM")[j])
cat("\nEstimaci{\’o}n bootstrap de la varianza: ", paste(round(Var, digits
=5), " (", names(Var), ")", sep="", collapse="
"))
Sd <- structure(sapply(theta.boot, sd), names=c("BWO","MM")[j])
69
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
cat("\nError est{\’a}ndar: ", paste(round(Sd, digits=5), " (", names(Var), "
)", sep="", collapse="
"))
sesgo <- structure(av - theta0, names=c("BWO","MM")[j])
cat("\nEstimaci{\’o}n bootstrap del sesgo: ", paste(round(sesgo, digits=5),
" (", names(Var), ")", sep="", collapse="
"))
par(mfrow=c(length(theta.boot),1))
if (is.element(variante, c("BWO", "all"))){
hist(theta.boot$BWO, freq=TRUE, main="Distribuci{\’o}n de las
estimaciones bootstrap (BWO)", axes=FALSE, xlab = "", ylab="", col=
terrain.colors(20))
a <- diff(par()$usr[1:2])
axis(1, line = 0.25, at = round(seq(par()$usr[1]+0.04*a, par()$usr
[2]-0.04*a, length.out=5L), digits=2))
axis(2, line = 0.25, at = round(seq(0, par()$usr[4]/1.04, length.out=5L)
), las=1)
}
if (is.element(variante, c("MM", "all"))){
hist(theta.boot$MM, freq=TRUE, main="Distribuci{\’o}n de las
estimaciones bootstrap (MM)", axes=FALSE, xlab = "", ylab="", col=
terrain.colors(20))
a <- diff(par()$usr[1:2])
axis(1, line = 0.25, at = round(seq(par()$usr[1]+0.04*a, par()$usr
[2]-0.04*a, length.out=5L), digits=2))
axis(2, line = 0.25, at = round(seq(0, par()$usr[4]/1.04, length.out=5L)
), las=1)
}
cat("\n")
70
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
out <- list(t0 = theta0, t = theta.boot, mean = av, var = Var, sd = Sd, bias
= sesgo, data = data, st = statistic, N = N, m = m)
invisible(out)
}
71
Apéndice
B
Diseños muestrales y estimadores usuales
Algunos diseños muestrales
srs wor
muestreo aleatorio simple con reemplazamiento
srs wr
muestreo aleatorio simple sin reemplazamiento
pps wor
muestreo con probabilidades proporcionales al tamaño muestral sin reemplazamiento
pps wr
muestreo con probabilidades proporcionales al tamaño muestral con reemplazamiento
pps wr + srs wor
Etapa 1: muestreo con probabilidades proporcionales al tamaño muestral con reemplazamiento
Etapa 2: muestreo aleatorio simple con reemplazamiento
pps wor + srs wor
Etapa 1: muestreo con probabilidades proporcionales al tamaño muestral sin reemplazamiento
Etapa 2: muestreo aleatorio simple con reemplazamiento
L strata
muestreo estratificado
NOTA: En este documento todas las menciones a los estimadores usuales de la varianza hacen referencia
a los estimadores de la varianza de la siguiente tabla, a menos que se especifique lo contrario.
72
·
n
N
73
L strata
pps wor + srs wor
pps wr + srs wor
1
n
·
PL
Yb = h=1 Ybh
πi = n · pi
Mi ·y i.
πi
Mi ·y i.
i=1
pi
Pn
·
Pn
Yb.. = i=1
Yb.. =
Yb =
pps wr
yi
i=1 pi
Pn
1
n
Pn
Yb = i=1
yi
yi
yi
πi
i=1
i=1
Pn
f=
1
f
Yb = N ·
Yb =
Pn
Estimador
pps wor
srs wr
srs wor
Diseño
i=1
Yi − Y
·
Yi.
pi
Mi2
i=1 πi
· (1 − f2i ) ·
Si2
mi
PL
V ar[Yb ] = h=1 V ar[Ybh ]
PN
−
+
−
2
2
Yi.
πi
Si2
mi
− Y..
· (1 − f2i ) ·
i=1 pi ·
Pn
PN PN
V ar[Yb.. ] = i=1 j>i (πi · πj − πij ) ·
+
Yi
πi
pi · (Zi − Y )
Yi
pi
i=1
Zi =
·
PN
Mi2
i=1 pi
1
n
1
n
PN
V ar[Yb.. ] =
i=1
PN
j>i (πi · πj − πij ) ·
1
N
PN PN
σ2 =
+ n1 ·
Yj
πj
2
+
v[Yb ] =
s2 =
1
n
·
·
Yj.
πj
2
v[Yb.. ] =
i=1
Pn
·
i=1
v[Yb ] =
Mi2
i=1 πi
Pn
·
h=1
2
yi
πi
v[Ybh ]
−
s2i
mi
Mi ·y i.
πi
Mj ·y j.
πj
− Yb..
2
2
yj
πj
2
−
zi − Yb
Mi ·y i.
pi
·
· (1 − f2i ) ·
PL
2
(yi − ȳ)
i=1
Pn
Pn
·
πi ·πj −πij
j>i
πij
1
n·(n−1)
1
n·(n−1)
Pn
+
i=1
Pn
v[Yb.. ] =
v[Yb ] =
i=1
·
s2
n
yi
πi ·πj −πij
j>i
πij
PN PN
1
n−1
s2
n
(yi − ȳ)
i=1
Pn
i=1
Pn
v[Yb ] = N 2 ·
1
n−1
σ2
n
2
s2 =
V ar[Yb ] = N 2 ·
PN
2
y=
·
Yi − Y
v[Yb ] = N 2 · (1 − f ) ·
Yi
1
N
i=1
PN
S2
n
Estimador usual de la Varianza
i=1
V ar[Yb ] =
V ar[Yb ] =
1
N −1
Y =
S2 =
V ar[Yb ] = N 2 · (1 − f ) ·
Varianza
2
+
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
Bibliografı́a
[1] Arnold, S.F.- Gibbs Sampling. Handbook of Statistics 9: Computational Statistics. North
Holland. 1993.
[2] Beran, R.- Jackknife approximations to bootstrap estimates. Ann. Statist., 12, 101-118.
1984.
[3] Bickel, P.J., & Freedman, D.A.- Some asymptotic theory for the bootstrap. Ann. Statist.,
9, 1196-1217. 1981.
[4] Chambers, R.L. & Skinner, C.J. ed.- Analysis of Survey Data, Wiley Series in Survey
Methodology. Wiley. 2003.
[5] Davison, A.C. & Hinkley, D.V.- Bootstrap Methods and Their Applications. Cambridge
University Press. 1997.
[6] Diciccio, T.J., & Romano, J.P.- A review of bootstrap confidence intervals. J.R.S.S. B, 50,
338-354. 1988.
[7] Diciccio, T.J., & Efron, B.- Bootstrap confidence intervals. Stat. Science. 11, 189-228. 1996.
[8] Efron, B.- Bootstrap Methods: Another Look at the Jackknife. Ann. Statist., 7, 1-26. 1979.
[9] Efron, B.- Better bootstrap confidence intervals. J.A.S.A., 82, 171-200. 1987.
[10] Efron, B., & Tibshirani, R.J.- An introduction to the bootstrap. Chapman & Hall. 1993.
[11] Everitt, B. S. & Hothorn, T.- A Handbook of Statistical Analyses Using R. 2006.
74
Bootstrap en poblaciones finitas
Samuel Nicolás Gil Abreu
[12] Freedman, D.A.- Bootstrap regresion models. Ann. Statist., 9, 1218-1228. 1981.
[13] Gambino, J.G.- PPS: Functions for PPS sampling. 2005.
[14] Ghosh, M. et al.- A note on bootstrapping the sample median. Ann. Statist., 12, 1130-1135.
1984.
[15] Hall, P.- On the bootstrap and confidence intervals. Ann. Statists., 14, 1431-1452. 1986.
[16] Hinkley D. V.- Bootstrap methods. J.R.S.S. B, 50, 321-337. 1988.
[17] LePage, R. & Billard, L. eds.- Exploring the limits of boostrap. J. Wiley. 1992.
[18] Lumley, T.- Survey: analysis of complex survey samples. 2010.
[19] Maindonald, J. & Braun, J.- Data Analysis and Graphics Using R. Cambridge University
Press. 2007.
[20] Mooney, C.Z. & Duval, R.D.- Bootstrapping: A nonparametric approach to statistical
inference. Beverly Hill: Sage Publication. 1993.
[21] Rao, C.R. ed.- Handbook of Statistics 9: Computational Statistics. North-Holland. 1993.
[22] Rizzo, M.- Statistical Computing with R. Chapman & Hall. 2007.
[23] Thompson, M.E.- Theory of Sample Surveys. Chapman & Hall. 1997.
[24] Wu, C.F.J.- Jackknife, bootstrap and other resampling methods in regresion analysis. Ann.
Statist., 14, 1261-1295. 1986.
[25] Wolter, K. M.- Introduction to Variance Estimation. Springer, 5. 1985.
75