Unidad 3 Formulación de problemas de programación lineal

Unidad 3
Formulación de problemas de programación lineal
La programación lineal es una herramienta para representar, buscar la solución y
analizar problemas de optimización; esto es, maximizar o minimizar algún objetivo; en
estos problemas hay que decidir cómo realizar diversas acciones o productos que compiten por recursos limitados o escasos. Para utilizar este modelo es necesario que tanto
el objetivo como las restricciones que representan las distintas condiciones del problema se puedan formular con funciones lineales.
La gran ventaja del modelo de la programación lineal (pl) dentro de la investigación
de operaciones es que se trata de una estructura general que puede servir para representar de manera apropiada aplicaciones de campos muy diversos con un método o varios
métodos de solución sencillos, que, por sus características, es fácilmente programable.
La pl ha sido utilizada con éxito en problemas reales de planeación de producción,
campañas publicitarias, carteras financieras, para establecer “turnos de personal”, realizar mezclas de productos, o bien para los problemas clásicos de transporte, de ruta más
corta, asignación, flujo máximo e inventarios. A continuación se presentará una serie
de ejemplos de problemas típicos que por supuesto no intenta ser exhaustiva, pero sí
pretende ayudar en este paso que suele ser muy difícil para los estudiantes: la formulación del modelo matemático a partir de un problema “real”, expresado en el lenguaje
coloquial.
Los problemas abarcan una gran cantidad de temáticas: problemas de producción,
administración y finanzas, de administración pública y para la toma de decisiones en
las políticas públicas; problemas ecológicos, sanitarios y de medio ambiente. En algunos casos el objetivo es fácilmente cuantificable, como obtener la máxima utilidad; en
otros, especialmente cuando el objetivo es la salud o el bienestar social, no es tan sencillo medirlo, y deberá analizarse cuidadosamente cómo plantear tales objetivos.
Pero sin importar el tipo de problema, para su formulación, en particular en los de
pl, el paso fundamental es la definición de las variables; se trata de aquello que necesitamos decidir: qué y cuánto hacer de las diversas acciones o productos que constituyen
las incógnitas del problema.
El siguiente paso es definir el objetivo del problema. En los modelos de pl siempre
se querrá optimizar, esto es, minimizar o maximizar la función objetivo (fo) que estará
73
Programación lineal
dada por una combinación lineal de las variables de decisión definidas previamente. Tal
vez se pueda pensar que tener que decidir por un solo objetivo limita el tipo de problemas; esto no es así, puede haber otros objetivos expresados como una restricción de un
logro por cumplir.
Finalmente habrá que escribir las ecuaciones necesarias para representar las distintas
restricciones del problema, generalmente debido a recursos limitados, ya sean éstos materias primas, mano de obra o condiciones del mercado. Estas restricciones se complementan con las llamadas restricciones de no negatividad, que establecen que las variables
de decisión siempre deben ser positivas.
Problemas de planeación de la producción
Los problemas de planeación de la producción son los problemas más clásicos de pl.
En éstos hay que decidir cómo usar los recursos disponibles realizando una combinación de productos o actividades que compiten por los mismos recursos con el objetivo
de maximizar la utilidad. A los recursos limitados suelen agregarse restricciones del
mercado y compromisos de la empresa.
En estos problemas las variables de decisión son la cantidad de cada producto que
se debe producir; el objetivo es maximizar las utilidades de la empresa y está sujeto a
una serie de restricciones debido a las limitaciones impuestas por los recursos, como las
materias primas, la mano de obra, la energía, el número de máquinas disponibles; deberá escribirse una desigualdad por cada uno de los recursos necesarios para la fabricación de los productos. Pueden también existir restricciones en la demanda de los
distintos productos o actividades que han de realizarse.
Ejemplo 3.1
Una empresa maquiladora del norte del país dedicada a la producción de televisores y
pantallas para video y computadoras necesita planear la producción del siguiente mes
debido a la introducción de un nuevo producto y a que va a dejar de producir otros por
cambios en la demanda. La gerencia piensa que los próximos meses deberían dedicarse
a fabricar sólo cuatro productos: pantallas de cristal líquido de 20 y de 24 pulgadas y
los televisores planos de 24 y 50 pulgadas. Debido a las diferentes tecnologías, los televisores son producidos en la planta de Chihuahua, mientras que las pantallas se producen en la planta de Tijuana. El control de calidad y el empaque final se realiza en esta
última.
En el cuadro 3.1 se presentan las disponibilidades de tiempo en cada una de las
plantas; en el caso de Chihuahua hay dos departamentos, el de electrónica y el de ensamble final. En el mismo cuadro se indica la utilidad neta por cada tipo de equipo.
74
Formulación de problemas de programación lineal
Cuadro 3.1
Horas/unidad
Chihuahua
Productos
Elecrónica
Ensamble
Tijuana
Utilidad
Pantallas lcd
$
Pantalla de 20”
3.5
Pantalla de 24”
850
3.8
925
Televisor de 24”
2.25
2.5
800
Televisor de 50”
2.0
2.75
1 200
3 000
3 200
Capacidad (horas/mes)
5 000
Finalmente todos los productos deben pasar por los departamentos de control de
calidad y de empaque. La disponibilidad de tiempo y el número de equipos que se han
de procesar por hora se indica en el cuadro 3.2.
Cuadro 3.2
Unidades/hora
Productos
Control de calidad
Empaque
Pantalla de 20”
3.0
6
Pantalla de 24”
2.5
5
Televisor de 24”
1.5
5
Televisor de 50”
2.0
3
3 200
800
Capacidad (horas/mes)
El departamento de mercadotecnia ha decidido que se deben fabricar al menos 100
equipos de cada tipo para mantener su presencia en el mercado nacional.
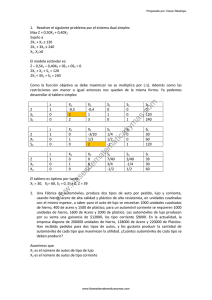
En primer lugar se deben definir las variables de decisión; en este problema hay cuatro
incógnitas que son la cantidad de cada equipo que conviene producir mensualmente:
x 1:
x 2:
x 3:
x 4:
la
la
la
la
cantidad
cantidad
cantidad
cantidad
de
de
de
de
pantallas de 20”
pantallas de 24”
televisores de 24”
televisores de 50”
El objetivo de la empresa es maximizar las utilidades, por lo tanto:
Máx U = 850x1 + 925x2 + 800x3 + 1 200x4
75
Programación lineal
Hay una serie de restricciones para la producción: el departamento de electrónica de
la planta de Chihuahua dispone de 3 000 horas mensuales que puede ocupar en producir la parte electrónica de ambos tipos de televisores, requiriendo 2.25 y 2 horas para
cada televisor de 24” y 50”, respectivamente, por lo tanto:
2.25x3 + 2x4 ≤ 3 000 horas
En el departamento donde se ensamblan estos televisores se cuenta con 3 250 horas:
2.5x3 + 2.75x4 ≤ 3 250 horas
En la planta de Tijuana se cuenta con 5 000 horas para la producción de las pantallas de cristal líquido tanto de 20” como de 24”, por lo tanto:
3.5x1 + 3.8x2 ≤ 5 000 horas
Todos los equipos deben ser sometidos a pruebas de calidad, y este departamento
cuenta con 3 200 horas al mes. Aquí se nos indica la cantidad de equipos que pueden
ser revisados en una hora; por ejemplo, nos dicen que en una hora se revisan 3 pantallas
lcd de 20”; esto quiere decir que se requieren 20 minutos o 1/3 de hora para cada pantalla; lo mismo habría que hacer para los demás equipos. Esta restricción se puede escribir de dos manera: en horas o en minutos, por lo tanto:
1/3x1 + 1/2.5x2 + 1/1.5x3 + 1/2x4 ≤ 3 200 horas
O en minutos:
20’ x1 + 24’ x2 + 40’ x3 + 30’ x4 ≤ 192 000 minutos
Ambas ecuaciones son equivalentes.
Por último para el empaque se cuenta con 800 horas, por lo tanto:
1/6x1 + 1/5x2 + 1/5x3 + 1/3x4 ≤ 800 horas
Falta agregar las restricciones impuestas por el departamento de mercadotecnia:
x1, x2, x3, x4 ≥ 100 equipos
El modelo del problema queda entonces así:
76
Formulación de problemas de programación lineal
Máx U = 850x1 + 925x2 + 800x3 + 1 200x4
s.a.
2.25x3 + 2x4 ≤ 3 000 horas
2.5x3 + 2.75x4 ≤ 3 250 horas
3.5x1 + 3.8x2 ≤ 5 000 horas
1/3x1 + 1/2.5x2 + 1/1.5x3 + 1/2x4≤ 3 200 horas
1/6x1 + 1/5x2 + 1/5x3 + 1/3x4 ≤ 800 horas
x1 ≥ 100 x2 ≥ 100
x3 ≥ 100
x4 ≥ 100
La solución de este sistema será la cantidad de equipos que se deben fabricar para
que se maximice la utilidad mensual de la empresa.
Problemas de planeación de campañas en medios de comunicación
Se trata de problemas en los que con un presupuesto limitado se quiere incidir en la
opinión del mayor número de personas utilizando diferentes medios de comunicación.
Como no es posible tratar de llegar al mayor número con el menor presupuesto, en
estos problemas se plantea cubrir al menos cierta cantidad de población con el menor
costo posible. Para presentar este problema se utilizará una variante de un problema
visto en la unidad 1.
Ejemplo 3.2
Una cadena de supermercados se va a instalar en un municipio que ya cuenta con otras
tiendas similares, por lo que ha decidido realizar una campaña publicitaria agresiva el
mes anterior a la inauguración. Tiene tres alternativas: anuncios en la televisión, anuncios en la radio local y folletos para entregar a domicilio. La experiencia obtenida en
localidades similares le indica que con cada anuncio en la televisión su mensaje llega a
500 personas, cada anuncio en la radio llega a 320 y de cada 1 000 folletos repartidos,
320 serán leídos por las personas. La población es de 260 000 habitantes, y la pretensión
es llegar a por lo menos 25% minimizando los costos de la campaña y utilizando estos
medios. El costo del millar de folletos, es de $400 siempre que el pedido sea por más de
10 millares de folletos y el costo de los anuncios en televisión es de $2 000 cada anuncio
si contrata al menos 20 anuncios mensuales; los anuncios en la radio cuestan $1 300 y
ofrecen un paquete mínimo de un anuncio diario durante una semana. Se ha decidido
utilizar los tres medios ya que llegan a públicos diferentes y sólo se cuenta con $75 000.
77
Programación lineal
En este problema hay que decidir cuántos anuncios de cada tipo contratar, con la
restricción de que se quiere usar los 3 medios. Por lo tanto, las variables de decisión son
éstas:
TV: número de anuncios en la televisión (al menos 20)
R: número de anuncios en la radio
F: cantidad de folletos a repartir (F = 1 equivale a 1 000 folletos)
La fo es minimizar el costo de la campaña
Mín costo = 2 000 TV + 1 300 R + 400 F
Se quiere llegar por lo menos a 25% de la población de 260 000 habitantes:
500 TV + 320 R + 320 F ≥ 65 000
El presupuesto máximo es de $ 75 000:
2 000TV + 1300 R + 400 F ≤ 75 000
además:
TV ≥ 20
R ≥ 7
F ≥ 10
El modelo entonces queda así:
Mín costo = 2 000 TV + 1 300 R + 400 F
s.a.
500TV + 320 R + 320 F ≥ 65 000
2 000TV + 1 300 R + 400 F ≤ 75 000
TV ≥ 20
R≥ 7
F≥ 10
La solución de este sistema será la mejor manera de realizar la campaña que cumpla
con los requisitos planteados.
78
Formulación de problemas de programación lineal
Problemas de planeación de carteras financieras
Se trata de cómo invertir una cantidad de dinero en varias opciones financieras con el
objeto de obtener el máximo rendimiento esperado, pero ajustándose a restricciones
que moderen el riesgo y permitan tener la liquidez requerida por el inversor.
Ejemplo 3.3
El señor Montaño García recibe en diciembre la cantidad de $220 000 en concepto de
aguinaldo, vacaciones y comisiones. Como no necesita utilizar ese dinero inmediatamente, consulta a un asesor financiero para analizar las distintas posibilidades para un
plan de inversión anual. Esta persona sabe que a mitad de año, en julio necesitará
$45 000 para saldar una deuda; además quisiera disponer, para cualquier emergencia,
de al menos 15% de este dinero.
El asesor le sugiere repartir el dinero en varias alternativas: 1) en este momento parece atractivo comprar dólares ya que están a $13.5 y se espera que para fin de año
lleguen a $15, pero debido a lo riesgoso sugiere que no se invierta más que 1/3 del dinero; 2) debido a la competencia que hay entre los bancos, Banorte está ofreciendo
6.8% si se depositan más de $80 000 en pagarés a 28 días, pero se deben dejar durante
6 meses; esta inversión permitiría retirar el dinero que necesita a mitad de año; 3) el
fondo de inversión Banefo ofrece un rendimiento esperado de 7.8%, aunque depende
de la tasa de los Cetes y por lo tanto también presenta riesgo, por lo que le sugiere no
invertir más de la mitad de lo que invierta en pagarés; 4) para poder tener dinero disponible, debe dejar cierta cantidad en una cuenta corriente cuyo rendimiento es de
1.2 por ciento.
Se trata de ayudar al señor Montaño a decidir cómo debe invertir su dinero en estas
cuatro opciones. Las variables de decisión serán éstas:
D: cantidad de dinero a invertir en dólares
P: cantidad de dinero a invertir en pagarés, de donde retirará $45 000 a los 6 meses
F: cantidad de dinero a invertir en el fondo Banefo
C: cantidad de dinero que se dejará en la cuenta corriente
El objetivo es maximizar el rendimiento. Si el dólar sube como se espera, la tasa de
interés equivalente será de (1.5)/(13.5) = 11.11%, superior a todas las demás. La fo
entonces será:
Máx R = 0.111 D + 0.034 P + 0.034 (P-45 000)+ 0.078 F + 0.012 C
79
Programación lineal
Pero por cuestiones de riesgo no se debe invertir más que la tercera parte en dólares:
D ≤ (1/3) 220 000
Para que Banorte dé la tasa de interés de 6.8% es necesario invertir al menos $80 000
pero como a mitad de año se retirarán $45 000, para que no baje la tasa deberán ser:
P ≥ 125 000
En cuanto a los fondos, debido a que son de interés variable también le recomendó
mesura:
F ≤ 1/2 P
Y para emergencias quiere disponer de 15% de su dinero:
C ≥ (0.15) 220 000
La suma de sus inversiones no puede exceder su capital, por lo que:
D + P + F + C ≤ 220 000
El modelo de pl de esta situación queda así:
Máx R = 0.111 D + 0.034 P + 0.034 (P-45 000)+ 0.078 F + 0.012 C
s.a.
D ≤ 73 333
P ≥ 125 000
F – (0.5) P ≤ 0
C ≥ 33 000
D + P + F + C ≤ 220 000
D, P, F, C ≥ 0
La solución de este sistema será la cantidad de dinero que debe invertirse en cada
una de las cuatro opciones para maximizar el rendimiento y conocer el rendimiento
esperado.
80
Formulación de problemas de programación lineal
Problema de dietas
El problema de las dietas se presenta cuando en una institución como una escuela o un
hospital debe diseñar una dieta que cumpla con ciertos requisitos mínimos de nutrientes, pero tratando de obtener el menor costo. El mismo tipo de problema sirve para
realizar dietas para adelgazar, por ejemplo, donde lo que se pretende es minimizar las
calorías, o para las granjas donde se debe alimentar animales utilizando aquellos productos que ofrezcan los nutrientes necesarios al menor precio. A continuación se da un
caso específico.
Ejemplo 3.4
Se necesita diseñar una dieta para estudiantes al menor costo posible pero satisfaciendo
sus necesidades básicas de 2 400 kcal diarias y de no menos de 1 000 g de comida; las
necesidades básicas también incluyen 2 l de agua, aunque el líquido no debe necesariamente provenir de los alimentos, y cantidades específicas de proteínas, grasas y carbohidratos. En el cuadro se indican las características de cada tipo de alimento por porción
de 100 g y los requerimientos diarios mínimos promedio para cada estudiante. La dieta debe también incluir al menos 1 huevo, 200 g de vegetales y 100 g de leche o queso.
Cuadro 3.3
Alimento
Grasas
(g)
Carbohidratos
(g)
Precio
($/kg)
8
1.4
52
20
66
11
11
1
25
110
72
2
0.2
23
15
250
55
30
4
0
42
kcal
Agua ml
Pan
245
38
Huevos (2)
150
Arroz
Pollo
Proteínas
(g)
Leche
66
90
3.6
3.6
4.8
10
Frijoles
110
67
6
1
21
12
Queso
250
50
20
15
0
55
35
80
2
0
18
13
100
50
375
Vegetales
Req. mínimo
2 400
2 litros
Variables de decisión. Es necesario saber cuántos gramos o porciones de cada alimento debe incluir la dieta. Debido a que la dieta se debe armar con los ocho alimentos
disponibles, el problema tiene ocho variables. Es conveniente expresar la dieta en porciones de 100 g ya que toda la información está dada por porción.
81
Programación lineal
x1: número de porciones de pan
x2: número de porciones de huevo
x3: número de porciones de arroz
x4: número de porciones de pollo
x5: número de porciones de leche
x6: número de porciones de frijoles
x7: número de porciones de queso
x8: número de porciones de vegetales
El objetivo es minimizar el costo. Como el precio está dado por kilogramos, y las
porciones son de 100 gramos, es necesario que los coeficientes de la fo sean calculados
previamente:
Mín C = 2x1 + 2.5x2 + 1.5x3 + 4.2x4 + 1x5 + 1.2x6 + 5.5x7 + 1.3x8
Las restricciones de esta dieta son cubrir cierta cantidad de calorías y una mínima de
gramos de alimento, y cubrir las necesidades de proteínas, grasas y carbohidratos que
necesita un estudiante para sus actividades normales. Nótese que no es necesario agregar una restricción respecto a la necesidad de agua de los individuos ya que este requerimiento no debe ser satisfecho con los alimentos solamente, sino que se complementa
con las bebidas. Las ecuaciones de las restricciones son las siguientes:
Calorías (kcal):
245x1 +150x2 + 110x3 + 250x4 + 66x5 + 110x6 + 250x7 + 35x8 ≥ 2 400
Cantidad de comida en peso (1 000 g = 10 porciones):
x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 ≥ 10
Proteínas ( g ):
8x1 + 11x2 + 2x3 + 30x4 + 3.6x5 + 6x6 + 20x7 + 2x8 ≥ 100
Grasas ( g ):
1.4x1 + 11x2 + 0.2x3 + 4x4 + 3.6x5 + 1x6 + 15x7 ≥ 50
Carbohidratos ( g ):
52x1 + 1x2 + 23x3 + 4.8x5 + 21x6 + 18x8 ≥ 375
Huevo (porciones):
x2 ≥ 0.5
Vegetales (porciones):
x8 ≥ 2
Lácteos (porciones):
x5 + x7 ≥ 1
82
Formulación de problemas de programación lineal
Como no puede haber cantidades negativas de alimentos, hay que agregar las restricciones de no negatividad; el modelo entonces queda así:
Mín Costo = 2x1 + 2.5x2 + 1.5x3 + 4.2x4 + x5 + 1.2x6 + 5.5x7 + 1.3x8
s.a.
245x1 + 150x2 + 110x3 + 250x4 + 66x5 + 110x6 + 250x7 + 35x8 ≥ 2 400
x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 ≥ 10
8x1 + 11x2 + 2x3 + 30x4 + 3.6x5 + 6x6 + 20x7 + 2x8 ≥ 100
1.4x1 + 11x2 + 0.2x3 + 4x4 + 3.6x5 + 1x6 + 15x7 ≥ 50
52x1 + 1x2 + 23x3 + 4.8x5 + 21x6 + 18x8 ≥ 375
x2 ≥ 0.5
x8 ≥ 2
x5 + x7 ≥ 1
x1, x2, x3, x4, x5, x6, x7, x8 ≥ 0
Problema de mezclas
Los problemas de mezclas se dan cuando para la elaboración de un producto, o varios,
se utiliza una serie de componentes o ingredientes en determinada proporción para dar
las características específicas a cada producto o mezcla. Por ejemplo, se utilizan distintas variedades de granos de café para lograr el grado de acidez, aroma y textura deseados; se mezclan semillas como cacahuate, pepitas, nueces, piñón, etcétera para venderlas
en empaques individuales; lo mismo ocurre cuando se produce acero en un horno de
fundición a partir de hierro y otros metales que le darán las características buscadas
según el tipo de uso para el que va a ser destinado dicho acero. Otro uso frecuente es
el diseño de dietas para animales a partir de ingredientes que puedan satisfacer los requerimientos nutricionales; este caso puede verse como el problema de dietas ya tratado. Se pueden encontrar ejemplos en la industria química, la petroquímica o en la de
cosméticos.
En todos estos problemas, el tomador de decisiones quiere minimizar el costo de
producir la mezcla que satisfaga los requerimientos impuestos, para lo cual debe indicar
la proporción de los distintos ingredientes que incluirá en la mezcla.
Ejemplo 3.5
En el estado de Veracruz se ha instalado una cooperativa de pequeños productores de
café para evitar venderlo a precios por debajo de los costos a los grandes acaparadores
internacionales. En ella se realizará la compra del café en cereza a los productores, el lavado, separación, secado y tostado para posteriormente molerlo, empacarlo y venderlo.
83
Programación lineal
Se ha pensado en vender dos estilos de café: gourmet y americano ya que son los más
consumidos en el mercado nacional. Aunque los gustos del consumidor nacional están
cambiando, actualmente la demanda de café estilo americano es mayor que la demanda
del estilo gourmet. En el cuadro 3.4 se indican los precios que pagará la cooperativa por
la tonelada de café en cereza:
Cuadro 3.4
Variedades
Precio $/t
Robusta
3 750
Arábica borbón
4 450
Arábica caturra
4 100
No especificado
2 800
Debido a las diferentes características de cada especie de café, se necesita mezclarlas
en diferentes proporciones para obtener las mezclas apropiadas para los estilos gourmet
y americano. La variedad arábica tiene un sabor delicado, aroma intenso y mayor cantidad de cafeína; la planta requiere de cuidados y de la sombra de grandes árboles,
mientras que la variedad robusta, como su nombre lo indica, es más resistente, es una
planta de mayor tamaño y rendimiento, de sabor más fuerte.
Entre los productores hay un grupo de la sierra de Zongolica que es de origen náhuatl y que están comenzando con la explotación de café, pero este año tendrán una
producción de no muy buena calidad. Aun así la cooperativa se ha comprometido a
que al menos 10% del volumen que se procese provenga de esta región.
En el cuadro 3.5 se especifican los requerimientos que debe cumplir cada uno de los
estilos de café.
Cuadro 3.5
Robusta
Arábica borbón
Americano
Gourmet
menos de 30%
menos de 8%
más de 15%
más de 25%
menos de 55%
Arábica caturra
Revuelto
más de 25%
más de 25%
menos de 80%
menos de 65%
menos de 25%
menos de 12%
84
Formulación de problemas de programación lineal
Es necesario establecer la cantidad o el porcentaje de cada tipo de grano con que se
realizará la mezcla para cada uno de los estilos de café. El porcentaje de cada ingrediente de la mezcla para obtener el costo mínimo es independiente de la cantidad, ya sea
que se trate de producir un kilogramo o una tonelada o cualquier otra cantidad. Así,
para definir las variables se puede establecer lo siguiente:
xij: cantidad del ingrediente i a utilizar en 1 kg de la mezcla j, expresada en kg
con i = 1,...4 y j = 1, 2, donde:
i = 1 robusta, j = 1 americano,
i = 2 borbón, j = 2 gourmet
i = 3 caturra,
i = 4 revuelto,
En este caso empezaremos por plantear las restricciones. Consideremos la restricción que dice que el café estilo americano no debe contener más que 30% de grano del
tipo robusta. La cantidad de robusta en 1 kg de café americano es x11 y sabemos que
debe ser menor o igual a 30% del total de la mezcla.
x11 ≤ 0.30 total de la mezcla
También sabemos que el total de la mezcla de café americano debe estar formado
por la suma de cada uno de los cuatro ingredientes:
x11 ≤ 0.3 (x11 + x21 + x31 + x41)
Esta ecuación se puede rescribir como
0.7 x11 − 0.3 x21 − 0.3 x31 − 0.3 x41 ≤ 0
De la misma manera se pueden escribir el resto de las restricciones.
Para el café estilo americano
x21 ≥ 0.15 (x11 + x21 + x31 + x41) (mínimo de borbón)
x21 ≤ 0.55 (x11 + x21 + x31 + x41) (máximo de borbón)
x31 ≥ 0.25 (x11 + x21 + x31 + x41) (mínimo de caturra)
x31 ≤ 0.80 (x11 + x21 + x31 + x41) (máximo de caturra)
x41 ≤ 0.25 (x11 + x21 + x31 + x41) (máximo revuelto)
85
Programación lineal
Para el café estilo gourmet:
x12 ≤ 0.08 (x12 + x22 + x32 + x42) (máximo de robusta)
x22 ≥ 0.25 (x12 + x22 + x32 + x42) (mínimo de borbón)
x32 ≥ 0.25 (x12 + x22 + x32 + x42) (mínimo de caturra)
x32 ≤ 0.65 (x12 + x22 + x32 + x42) (máximo de caturra)
x42 ≤ 0.12 (x12 + x22 + x32 + x42) (máximo revuelto)
Por último se quiere que al menos 10% sea del café de la sierra de Zongolica:
x41 + x42 ≥ 0.1 (x11 + x21 + x31 + x41 + x12 + x22 + x32 + x42)
Además es necesario que la suma de los ingredientes sea 1 kg:
x11 + x21 + x31 + x41 = 1 kg
x12 + x22 + x32 + x42 = 1 kg
Como las variables fueron definidas como la parte de cada ingrediente que debe
llevar 1 kg de mezcla, las últimas ecuaciones son igualdades estrictas.
Por último, el objetivo es obtener las mezclas más económicas, por lo que la fo
queda así:
Mín costo = 3.75x11 + 4.45x21 + 4.10x31 + 2.80x41 + 3.75x12 +4.45x22 + 4.10x32 + 2.80x42
El modelo de pl obtenido para este problema de mezclas es el siguiente:
Mín costo = 3.75x11 + 4.45x21 + 4.1x31 + 2.8x41 + 3.75x12 + 4.45x22 + 4.1x32 + 2.8x42
s.a.
0.70x11 − 0.30x21 − 0.30x31 − 0.30x41 ≤ 0
-0.15x11 + 0.85x21 − 0.15x31 − 0.15x41 ≥ 0
-0.55x11 + 0.45x21 − 0.55x31 − 0.55x41 ≤ 0
-0.25x11 − 0.25x21 + 0.75x31 − 0.25x41 ≥ 0
-0.80x11 − 0.80x21 + 0.20x31 − 0.80x41 ≤ 0
-0.25x11 − 0.25x21 − 0.25x31 + 0.75x41 ≤ 0
0.92x12 − 0.08x22 − 0.08x32 − 0.08x42 ≤ 0
-0.25x12 + 0.75x22 − 0.25x32 − 0.25x42 ≥ 0
-0.25x12 − 0.25x22 + 0.75x32 − 0.25x42 ≥ 0
-0.65x12 − 0.65x22 + 0.35x32 − 0.65x42 ≤ 0
-0.12x12 − 0.12x22 − 0.12x32 + 0.88x42 ≤ 0
86
Formulación de problemas de programación lineal
x11 + x21 + x31 + x41 = 1
x12 + x22 + x32 + x42 = 1
-0.1x11 -0.1x21 -0.1x31 + 0.9x41 -0.1x12 -0.1x22 -0.1x32 + 0.9x42 ≥ 0
x11, x21, x31, x41, x12, x22, x32, x42 ≥ 0
Los problemas de mezclas suelen tener variantes; por ejemplo, puede ser que se tenga una oferta determinada de cada uno de los ingredientes, incluso puede estar especificada cierta demanda para cada uno de los productos resultantes. En esos casos,
convendrá definir las variables como la cantidad del ingrediente (i) que se utilizará para
la mezcla (j). Además habrá que escribir las ecuaciones de oferta y demanda para cada
una de las restricciones que especifique el problema. Por ejemplo, si se nos explicitara
que la demanda es de cinco toneladas de mezcla para café americano y dos toneladas
para café gourmet, con sólo variar las restricciones que indican el total se obtendría la
mezcla más adecuada para la nueva condición:
x11 + x21 + x31 + x41 = 5
x12 + x22 + x32 + x42 = 2
Si hubiera restricciones en la disponibilidad de alguno de los ingredientes, por
ejemplo, se dispone sólo de diez toneladas de granos de café Borbón, habría que definir
las variables en toneladas y agregar
x21 + x22 ≤ 10
El resultado indicaría cuanto de cada grano mezclar pero expresado en toneladas.
Problemas de asignación de turnos de personal
Estos problemas se presentan en los casos en que hay que cubrir diferentes requerimientos de personal a lo largo del día o de la semana, como serían los cajeros de un
supermercado o de un banco, los meseros, los turnos de vigilancia en edificios, etcétera.
Una condición implícita en estos problemas es que todos los empleados ganan lo mismo, y lo que se intenta es minimizar el número de personas necesarias para satisfacer
las necesidades. El siguiente ejemplo presenta este tipo de problema.
87
Programación lineal
Ejemplo 3.6
Se quieren reorganizar los turnos de las enfermeras de un hospital general que da atención a una ciudad de medio millón de habitantes. Las enfermeras trabajan turnos de 8
horas continuas, con excepción del turno nocturno de 12 horas (de 8 pm a 8 am). Hay
4 turnos diurnos que comienzan a las 6 am, 10 am, 2 pm y 6 pm. El número de enfermeras necesarias varía según las distintas tareas que deben realizarse como bañar a los
pacientes, darles de comer, asistir a los médicos en las consultas, realizar curaciones,
etcétera. La administración del hospital indica que el número de enfermeras mínimo
necesario es el siguiente:
Cuadro 3.6
Intervalo
Número mínimo de enfermeras
6a8
30
8 a 10
22
10 a 14
26
14 a 16
17
16 a 20
20
20 a 22
15
22 a 6
12
Para resolver este problema es importante entender cuál es la decisión que han de
tomar las autoridades del hospital. Como existen cuatro turnos diurnos y uno nocturno, es necesario decidir cuántas personas trabajarán en cada uno de los turnos, por lo
que se tienen cinco variables de decisión:
x 1:
x 2:
x 3:
x 4:
x 5:
cantidad
cantidad
cantidad
cantidad
cantidad
de
de
de
de
de
enfermeras
enfermeras
enfermeras
enfermeras
enfermeras
en
en
en
en
en
el turno
el turno
el turno
el turno
el turno
de
de
de
de
de
6 a 14
10 a 18
14 a 22
18 a 2
20 a 8
y por supuesto el objetivo es tener la menor cantidad de enfermeras pero que cubran
los requerimientos de personal para cada uno de los intervalos en que se conoce la
demanda.
Mín x1 + x2 + x3 + x4 + x5
Para plantear las restricciones hay que garantizar que se cumpla con el número mínimo necesario de enfermeras en cada intervalo. Por ejemplo, se sabe que entre las 6 y
88
Formulación de problemas de programación lineal
las 8 am se requieren de al menos 30 enfermeras; durante esas horas estarán las enfermeras del turno de la noche ya que su hora de salida es a las 8 am; además estarán las
que entran a las 6 am de la mañana. Esto se puede representar así:
x1 + x5 ≥ 30
En el intervalo de las 8 am a las 10 am se requieren 22 enfermeras. Dado que las
únicas que trabajan en ese horario son las del primer turno de la mañana, las que entran
a las 6 am, pues las del turno nocturno acaban de salir, entonces:
x1 ≥ 22
Habrá que seguir analizando cada uno de los intervalos, observando cuáles turnos
cubren dicho intervalo, y escribir las ecuaciones correspondientes. Para visualizar mejor
este tipo de problemas se puede utilizar una representación de tipo matricial, en las
que, por un lado, se ponen los turnos y, por el otro, los intervalos en los cuales deben
cumplirse ciertas restricciones. El cuadro 3.7 es la representación de la matriz de este
problema.
El primer renglón que corresponde al intervalo de 6 a 8 am muestra cuales son los
turnos que cubren ese intervalo. Como el primer turno tiene x1 enfermeras y el turno
nocturno x5 , la suma de ambas deberá ser al menos igual a las 30 enfermeras que se
requieren. Para el turno de 8 a 10 am solamente trabajan las del primer turno, mientras
que entre las 10 am y las 2 pm se dispondrá del personal que entró a las 6 am, así como
del que lo hizo a las 10 am.
Cuadro 3.7
Intervalos Subintervalos
X1
6 a 14
X2
10 a 18
X3
14 a 22
X4
18 a 2
X5
20 a 8
Número
mínimo de
enfermeras
06 a 08
30
08 a 10
22
10 a 14
26
14 a 16
17
16 a 20
16-18
20
18-20
20
20 a 22
22 a 06
15
22-02
12
02-06
12
89
Programación lineal
El cuadro 3.7 permite ver quiénes están trabajando simultáneamente en cada intervalo, lo que facilita la construcción de las ecuaciones.
Es importante notar que los intervalos en que se tienen determinados requisitos no
tienen por qué coincidir con los turnos de los trabajadores; esto se puede observar con
la restricción en que se especifica que entre las 16 y las 20 horas se necesitan 20 enfermeras. Al observar los horarios de inicio y fin de cada turno, se identifica un turno que
comienza dentro de dicho intervalo, por lo que durante esas cuatro horas del intervalo
no se contará con las mismas enfermeras, razón por la cual fue necesario dividir el intervalo en dos subintervalos, pero asegurándonos de que en ambos existiera el mínimo
de personal requerido para efectuar las labores. Se sugiere al alumno analizar qué ocurre
durante el intervalo de 10 pm a 6 am.
El problema queda modelado por el siguiente conjunto de ecuaciones:
Mín x1 + x2 + x3 + x4 + x5
s. a.
x1 + x5 ≥ 30
x1 ≥ 22
x1 + x2 ≥ 26
x2 + x3 ≥ 17
x2 + x3 ≥ 20
x3 + x4 ≥ 20
x3 + x4 + x5 ≥ 15
x4 + x5 ≥ 12
x5 ≥ 12
x1, x2, x3, x4, x5 ≥ 0
El modelo encontrado tiene 9 restricciones estructurales y las condiciones de no
negatividad. Sin embargo, si se revisan podemos notar que la cuarta y quinta restricciones tienen la misma expresión del lado izquierdo; asimismo, mientras que en la cuarta
se pide que haya por lo menos 17 enfermeras, en la quinta se exige que al menos sean
20, por lo que la primera de estas ecuaciones resulta una condición redundante y por
lo tanto puede quitarse del modelo sin afectar la solución.
Como ejercicio, vamos a buscar una solución posible que cumpla con los requerimientos mínimos, aunque no necesariamente sea la óptima. Empezaremos por aquellos turnos para los que hay límites mínimos establecidos. En el turno de la noche debe
haber al menos 12 personas, por lo tanto proponemos x5 = 12; además como de 8 a 10
am solamente está el personal que inicia su turno a las 6 am, se requiere que al menos
x1 = 22. Con eso queda satisfecha la necesidad de contar con 30 personas de 6 a 8 am,
ya que habrá 34. Desde las 10 am a las 2 pm se necesitan 26 enfermeras y ya se cuenta
con 22, por lo que x2 = 4, pero como luego se necesita que x2 + x3 ≥ 20, entonces x3 = 16.
90
Formulación de problemas de programación lineal
En el intervalo siguiente, de las 6 pm a las 8 pm se necesitan 20, por lo que x4 = 4. La
solución propuesta requiere de 22 + 4 + 16 + 4 + 12 = 58 enfermeras para cubrir las
necesidades diarias del hospital. Esta es una solución posible aunque no necesariamente óptima. En la siguiente unidad se aprenderá cómo resolver estos problemas para
encontrar la solución óptima.
Problemas de transporte
En los problemas de transporte hay un único producto, homogéneo, que se debe distribuir desde varios orígenes a varios destinos. Se acepta la hipótesis de que el producto
cuesta lo mismo cualquiera sea su origen, lo que varía es el costo del transporte. El
costo del transporte puede estar dado en cualquier tipo de unidades como $/t, $/camión, $/caja, etcétera, lo que interesa es minimizar el costo de surtir la demanda solicitada por los distintos destinos.
Ejemplo 3.7
La Zona Metropolitana del Valle de México (zmvm) tiene problemas de abasto de
agua en varias de sus colonias, especialmente al este de la ciudad. En este momento
las autoridades del Sistema de Aguas de la Ciudad de México, junto con la Comisión de Agua del Estado de México deben decidir cómo abastecer tres zonas que
están padeciendo un desabasto sistemático: Nezahualcóyotl, Iztapalapa y Los Reyes,
con necesidades de 3.4, 5 y 2.2 m3/s. Las fuentes de abastecimiento que se están
considerando son 3 sistemas de pozos profundos (uno de ellos del Estado de México), que aún tienen excedentes, y agua proveniente del sistema Cutzamala. El primer sistema puede abastecer 2 m3/s, el segundo, 2.5 m3/s, y el tercer sistema de
pozos, 2.5 m3/s; de la presa de Valle de Bravo, que forma parte del sistema Cutzamala, después de realizar obras de mantenimiento, se podrá extraer de 1 a 10 m3/s, según sea necesario. Los costos de abastecimiento, operación y conducción por m3/s
son éstos:
Cuadro 3.8
P1
P2
P3
Cutzamala
Iztapalapa
6.0
4.5
3.0
12.5
Los Reyes
3.5
3.0
4.5
12.0
Nezahualcóyotl
3.0
3.5
4.5
11.5
91
Programación lineal
Se debe encontrar la manera más económica de satisfacer la demanda de agua a los
lugares que la necesitan.
Es necesario decidir cuánta agua se enviará desde cada uno de los orígenes a cada
uno de los destinos. Este problema, además de pertenecer a los de pl, se puede analizar
como un problema de redes. Aquí utilizaremos la gráfica de redes correspondiente.
En el siguiente diagrama se representa cada punto origen con un círculo y cada destino también con un círculo, llamados nodos. Estos nodos están unidos por unas líneas
o flechas llamadas ramas, que indican los posibles flujos del agua.
Cada nodo representa un punto de origen u oferta o un punto de destino o demanda, por lo tanto cada nodo tiene asignada una cantidad que es la oferta o demanda
correspondiente. Las ramas representan un flujo o una acción, y a cada una de ellas se
asocia una variable que corresponde a la cantidad del flujo que se enviará del origen (i)
al destino (j). Cada rama tiene asociada también un parámetro que indica el costo de
enviar una unidad del origen (i) al destino (j).
Diagrama 3.1
2m3/s
P1
x11
c11= 6
x12
Iz
5m3/s
x21
2.5m3/s
P2
LR
2.2m3/s
N
3.4m3/s
x31
2.5m3/s
10m3/s
P3
x41
c43= 11.5
C
En este problema hay 12 variables de decisión que llamaremos xij donde xij es la
cantidad de agua medida en m3/seg, que va desde el origen i al destino j.
1: Iztapalapa
con i = 1: P1j =
2: P22: Los Reyes
3: P33: Nezahualcóyotl
4: Cutzamala
92
Formulación de problemas de programación lineal
El objetivo es satisfacer la demanda de agua en las tres delegaciones al menor costo
posible. Por lo tanto la fo se formulará como:
Mín = 6x11 + 3.5x12 + 3x13 + 4.5x21 +3x22 + 3.5x23 +
3x31 + 4.5x32 + 4.5x33 + 1 2.5x41 + 12x42 +11.5x43
Restricciones de la oferta. Cada uno de los pozos puede enviar cierto flujo de agua a cada
una de las tres delegaciones demandantes, pero la suma de los flujos enviados no puede
exceder la disponibilidad de ellos. Las restricciones son:
x11 +
x21 +
x31 +
x41 +
x12 +
x22 +
x32 +
x42 +
x13 ≤
x23 ≤
x33 ≤
x43 ≤
2
2.5
2.5
10
m3/s
m3/s
m3/s
m3/s
Restricciones de la demanda. Visto desde la demanda, cada destino puede recibir el líquido de cualquiera de las cuatro fuentes. Aquí es necesario analizar la situación para establecer el signo de las restricciones: puede ser que el demandante quiera exactamente la
cantidad demandada o al menos dicha cantidad. Pero como se trata de un caso de minimizar costos, seguramente la solución óptima hará que se cumpla la igualdad y por
lo tanto no enviará excedentes. Las restricciones son:
x11 + x21 + x31 + x41 ≥ 5
x12 + x22 + x32 + x42 ≥ 2.2
x31 + x32 + x33 + x34 ≥ 3.4
Como ningún flujo puede ser negativo –en ese caso significaría que el agua iría en
sentido inverso–, se plantean la condición de no negatividad:
x11, x21, x31, x41, x12, x22, x32, x42, x13, x23, x33, x34 ≥ 0
El sistema de ecuaciones resultante tiene características que lo hacen muy fácil de
resolver dado que todos los coeficientes son cero o uno y con una distribución muy
particular. Esta simplificación en el modelo permite utilizar una simplificación del método general de resolución de problemas de pl, llamado “método de transporte”. Este
método se explica en la unidad 6, aunque estos problemas también se pueden resolver
con el método general, el método Simplex y se puede resolver con los paquetes tradicionales para pl.
93
Programación lineal
A continuación se presentan dos problemas que comparten varias características
de los problemas de transporte; se trata de los problemas de transporte con transbordo
y de los problemas llamados de asignación de recursos.
Problemas de transporte con transbordo
Los problemas de transporte con transbordo son muy similares a los de transporte:
existen puntos de oferta con determinadas cantidades disponibles de cierto producto,
y otros puntos destino que demandan dicho producto, pero además pueden existir
puntos intermedios donde llega mercancía de varios orígenes y que desde allí se distribuye a los puntos de demanda.
A continuación se muestra el diagrama de redes de un problema de este tipo. Igual
que en el problema de transporte, cada rama deberá ser representada por una variable,
y habrá que escribir una restricción por cada nodo de la gráfica. En un nodo de transbordo la suma de lo que llega debe ser igual a lo que sale. En un nodo que funcione
como punto intermedio y como destino, la suma de lo que llega deberá ser igual a lo
que se queda más lo que sale.
Diagrama 3.2
1
O1
x1T
T
O2
2
x2T
1
xT1
xD21
xT2
x22
2
O3
3
D1
D2
x32
En el diagrama 3.2 se pueden contar siete ramas, por lo que el problema tiene siete
variables de decisión, y existen seis nodos, para los cuales hay que plantear las ecuaciones de equilibrio:
x1T≤ oferta1
x2T + x22 ≤ oferta2
x32≤ oferta2
94
Formulación de problemas de programación lineal
xT1 + xD21 ≥ D1
x22 + x32 + xT2 ≥ D2 + xD21
x1T + x2T = xT1 + xT2
El objetivo es minimizar el costo del transporte, entonces la fo será:
Mín C = Σ Σ cij xij
donde cij son los costos unitarios de cada trayecto.
Problemas de asignación
Los problemas de asignación son aquellos en que es necesario “asignar” personas a tareas específicas; máquinas a distintos operarios o vendedores a diferentes rutas, maestros a grupos de alumnos, etcétera. El costo o el rendimiento de asignar a determinado
individuo cada una de las tareas varía de acuerdo a sus capacidades particulares. El
objetivo generalmente es minimizar el costo de la asignación o el tiempo en que se produzca el trabajo. En algunos casos puede ser más conveniente plantear maximizar la
utilidad obtenida por esas tareas.
Ejemplo 3.8
Una empresa de publicidad en expansión acaba de seleccionar a cinco nuevos empleados con capacidades profesionales: dos son licenciados en comunicación y los otros tres
son diseñadores gráficos con entrenamiento y experiencias diversas que pueden ser
útiles a la empresa. Debido a que las vacantes son de diferente responsabilidad y considerando las habilidades personales, el departamento de recursos humanos realizó la siguiente matriz en la que se indica el salario que debería pagarse a cada uno de los
individuos para las distintas funciones que podría desempeñar.
Cuadro 3.9
Puesto 1
Puesto 2
Puesto 3
Puesto 4
Puesto 5
C1
7 000
7 250
7 250
—
10 000
C2
6 500
7 500
7 000
6 000
—
DG1
5 800
—
7 000
7 000
8 500
DG2
6 000
6 500
5 700
6 500
—
DG3
5 500
7 000
—
7 000
9 500
95
Programación lineal
La empresa quiere colocar a cada uno de los nuevos empleados en los distintos
puestos de manera que la nómina a pagar sea la menor posible, dado que el proyecto
en que está trabajando la empresa lo empezará a cobrar seis meses después, por lo que
tendrá que obtener un préstamo bancario para mantenerse hasta ese momento.
Diagrama 3.3
C2
C1
x15
x11
7 000
DG1
DG3
6 000
10 000
x29
x12
7 250
P1
DG2
P2
P3
P4
P5
En este caso se puede hacer un diagrama de red como en los problemas de transporte, en el que existirá una rama entre cada uno de los empleados y los puestos que puede
ocupar. A cada rama le corresponderá un costo que indica la matriz de salarios. Y como
en los problemas de transporte, a cada rama se le asigna una variable. Aquí es donde
aparece la diferencia fundamental entre los problemas de transporte y los de asignación: cada una de las variables xij sólo puede tomar dos valores, 1 y 0:
xij = 1 si el empleado i se asigna al puesto j
= 0 si el empleado i no se asigna al puesto j
La fo es:
Mín C = Σ c1j x1j + Σ c2j x2j + Σ c3j x3j + Σ c4j x4j + Σ c5j x5j
Las restricciones corresponden a cada nodo; por ejemplo, el primer empleado puede ser colocado en cualquiera de los puestos, excepto el puesto 4, pero si ocupa un
96
Formulación de problemas de programación lineal
puesto, ya no puede estar en ninguno de los otros; por lo que la restricción correspondiente será:
x11 + x12 + x13 + x15 = 1
E igual para los otros empleados:
x21 + x22 + x23 + x24 =
x31 + x33 + x34 + x35 =
x41 + x42 + x43 + x44 =
x51 + x52 + x54 + x55 =
1
1
1
1
Lo mismo pasa con los puestos ya que sólo una persona podrá ocupar cada puesto:
x11 + x21 + x31 + x41 + x51 = 1
x12 + x22 + x42 + x52 = 1
x13 + x23 + x33 + x43 = 1
x24 + x34 + x44 + x54 = 1
x15 + x35 + x55 = 1
Además:
xij ∈ {0, 1}
La resolución de estos problemas requiere que se agregue esta condición y existen
programas de cómputo para resolverlos.
Problemas de inventarios
Todos los problemas presentados hasta ahora no tomaban en cuenta el tiempo, esto es, se
planea la mejor manera de realizar una serie de actividades y éstas se ejecutan una sola vez,
o se repiten de la misma manera en los periodos siguientes. A este tipo de modelos podemos llamarlos “estáticos”. Los problemas de inventarios, por el contrario, corresponden a
modelos dinámicos en los que el valor que toma una variable en un periodo depende del
valor que tenía en el periodo anterior: x t + 1 = f (x t ). En estos problemas es necesario analizar lo que ocurre a lo largo de un ciclo, sea éste un año, un mes, una semana; no interesa optimizar cada periodo por separado, sino el rendimiento en el ciclo completo.
El problema que analizaremos es un típico problema administrativo en el que, por
ejemplo, se conoce la demanda mensual de cierto producto durante todo el año. En
97
Programación lineal
general casi todos los productos tienen demandas cíclicas; por ejemplo, los uniformes
escolares se venden al comienzo del año escolar; los electrodomésticos, a fin de año
porque la gente utiliza el aguinaldo para comprar bienes duraderos o también para celebrar el día de la madre (aunque sería mejor regalar flores que una plancha); hay comidas típicas de determinadas fiestas; ropa para frío o para calor, etcétera. Por otro lado,
para las empresas no es fácil cambiar sus productos o volúmenes de producción de un
momento a otro; si producen a ritmo constante para satisfacer los meses de menor demanda, se perderán la posibilidad de vender cuando la demanda crezca y si producen
por encima de la demanda de ciertos meses tendrán que pagar el costo financiero de la
inversión que no puedan vender inmediatamente y pagar los costos de almacenamiento, seguros y los costos administrativos del manejo de estos inventarios.
Ejemplo 3.9
En octubre una empresa automotriz debe planear su producción del siguiente año para
satisfacer la demanda de su modelo más económico en función de los pedidos anticipados. En el cuadro 3.10 se muestra la demanda en miles de carros para cada bimestre.
Se ha estimado que el costo de tener que mantener un carro de un bimestre al otro más
los costos del seguro y del personal de vigilancia es de $420 bimestrales. Los costos de
producción de los vehículos también varían a lo largo del año pues en el mes de marzo
se espera un aumento en los salarios de 5% y los costos de los insumos también se incrementan. También se han estimado estos costos y se muestran en el cuadro 3.10. El
precio de venta es el mismo durante todo el año. Al comenzar el siguiente año se dispondrá de 2 000 vehículos, este es el inventario inicial y se quiere que para el año siguiente queden al menos 2 200 vehículos. Por políticas de la empresa, ningún pedido
debe quedar sin satisfacerse totalmente.
Cuadro 3.10
Bimestre
1
2
3
4
5
6
Demanda
6
3.5
3
3
4
6.5
Costo total
38 000
39 600
39 750
40 100
40 400
41 000
Planear la producción implica determinar el número de carros que se han de producir cada bimestre, o sea, habrá seis variables de decisión:
xi: miles de carros a producir en el bimestre i: i ={1,2...6}
98
Formulación de problemas de programación lineal
Pero también hay otras variables que conviene definir:
di: demanda durante el intervalo i en miles de carros (dato en este problema)
Ii: inventario o sobrante del intervalo i en miles de carros
El número de carros que se han de producir en el primer bimestre deberá ser:
x1 = d1 + I1 – I0
esto es la demanda del bimestre más los que se queden para el siguiente menos los carros que se tenían del periodo anterior. En este caso conocemos la demanda y el inventario inicial:
d1 = 6
I0 = 2
Pero la cantidad de carros que nos conviene producir y almacenar para el siguiente
período también es una incógnita. La ecuación entonces queda así:
x1 = 6 + I1 – 2 = 4 + I1
O el inventario del periodo será:
I1 = x1 + I0 – d1 = x1 – 4
El inventario al final del periodo es igual a lo que se produce en el periodo más lo
que había en existencia menos lo que se vende.
Para el segundo bimestre el inventario será igual a lo que se produzca en ese bimestre más lo que había quedado menos lo que se venda:
I2 = x2 + I1 – d2 = x2 + I1 – 3.5
Y de igual manera para los siguientes bimestres:
I3 =
I4 =
I5 =
I6 =
x3 +
x4 +
x5 +
x6 +
I2 – d3 = x3 + I2 – 3
I3 – d4 = x4 + I3 – 3
I4 – d5 = x5 + I4 – 4
I5 – d6
99
Programación lineal
Pero como se quiere que el sexto bimestre queden 2 200 carros para el año siguiente, entonces:
I6 = 2.2 = x6 + I5 – 6.5
Entonces el problema tiene 11 variables de decisión, ya que en este caso I6 fue dato:
xi: miles de carros a producir en el bimestre i : i ={1,2..6}
Ii: miles de carros que quedan del periodo i al i + 1 con i ={1, 2, 3, 4, 5}
El objetivo de la empresa es minimizar los costos de producción y de inventarios a
lo largo del año:
Mín C = Σ cj xj + Σ kj Ij
Donde cj es el costo de producción unitario y kj es el costo de almacenaje de los carros. Como las variables de decisión indican los miles de carros a producir, la fo queda así:
Mín C =[38 000 x1 + 39 600 x2 +39 750 x3 + 40 100 x4 + 40 400 x5+ 41 000 x6
+ 420 ( I1 + I2 + I3 + I4 + I5 + I6 )] 1 000
s.a.
x1 – I1 = 4
x2 + I1 – I2 = 3.5
x3 + I2 – I3 = 3
x4 + I3 – I4 = 3
x5 + I4 – I5 = 4
x6 + I5 = 8.7
Además: xi, Ii ≥ 0
Nota: este ejemplo no cubre todos los aspectos que se ven en el estudio de los problemas de inventarios, pero sirve como introducción a modelos dinámicos y muestra
cómo la pl puede utilizarse cuando se trata de optimizar en problemas en los que el
tiempo es un componente fundamental.1 Este esquema de planteamiento es utilizado
para la planeación de la comercialización de cualquier producto. Para mostrar este tipo
de aplicación se presenta el siguiente caso.
1 Otros problemas que no se presentan en el presente texto, pero que tienen características similares,
son los problemas financieros en los que se quiere invertir, pero que debe considerarse el flujo de dinero en
el tiempo.
100
Formulación de problemas de programación lineal
Ejemplo 3.10
La comercializadora de granos MaizMex se dedica a la compra y venta de maíz al contado; posee una bodega con capacidad para 520 toneladas. El 1° de enero tiene un inventario de 100 t y $2 000 000 en caja. La empresa debe planear sus compras y ventas
para el trimestre ya que se tienen los precios a futuro. En el cuadro 3.11 se muestran
los precios por tonelada de enero a marzo. Por las condiciones de transporte y entrega
lo que se compra en un mes no puede ser vendido hasta el siguiente mes. Al final del
trimestre se quiere contar con un inventario de 200 toneladas.2
Cuadro 3.11
Mes
Precio compra
Precio venta
Enero
$2 850
$3 100
Febrero
$3 050
$3 250
Marzo
$2 900
$2 950
Para realizar el programa de compras y ventas se deben definir las variables del problema; en este caso se propone
xe, xf y xm : toneladas a comprar los meses de enero, febrero y marzo
ye, yf y ym: toneladas a vender los meses de enero, febrero y marzo
I1 e I2: inventarios en toneladas al finalizar enero y febrero
C1 y C2: capital disponible a fines de enero y febrero
El objetivo es maximizar la utilidad:
fo: Máx U = 3 100ye + 3 250yf + 2 950ym – 2 850xe – 3 050xf – 2 900xm
Las restricciones son para cada mes; las de enero son éstas:
1) Espacio: Io + xe – ye ≤ 520 t → xe – ye ≤ 420
2) Capacidad de compra: 2 850xe ≤ Co = $2 000 000 → 2 850xe ≤ 2 000 000
3) Venta máxima: ye ≤ Io→ ye ≤ 100
Para simplificar el problema se agrega la definición de dos variables:
2 Este
problema fue adaptado de Moskowitz, H. Y Wrigth, G., Investigación de operaciones, PHH.
101
Programación lineal
4) Inventario a fin de mes:
I1 = Io + xe – ye → I1 – xe + ye = 100
5) Capital a fin de mes:
C1 = Co + 3 100ye – 2 850xe → C1 – 3 100ye + 2 850xe = 2 000 000
Para el mes de febrero:
1) I1 + xf – yf ≤ 520→
2) 3 050xf ≤ C1→
3) yf ≤ I1→
4) I2 = I1 + xf – yf→
5) C2 = C1 + 3 250yf – 3 050xf →
I1 + xf – yf ≤ 520
3 050xf – C1 ≤ 0
yf – I1 ≤ 0
I2 – I1 – xf + yf = 0
C2 – C1 – 3 250yf + 3 050xf = 0
I2 + xm – ym ≤ 520
2 900xm – C2 ≤ 0
ym – I2 ≤ 0
I2 + xm – ym = 200
Para el mes de marzo:
1) I2 + xm – ym ≤ 520→
2) 2 900xm ≤ C2→
3) ym ≤ I2→
4) I3 = 200 = I2 + xm – ym →
El modelo entonces queda como sigue:
fo: Máx U = 3 100ye + 3 250yf + 2 950ym – 2 850xe – 3 050xf – 2 900xm
s. a.
xe – ye ≤ 420
2 850xe ≤ 2 000 000
ye ≤ 100
I1 – xe + ye = 100
C1 – 3 100ye + 2 850xe = 2 000 000
I1 + xf – yf ≤ 520
3 050xf – C1 ≤ 0
yf – I1 ≤ 0
I2 – I1 – xf + yf = 0
C2 – C1 – 3 250yf + 3 050xf = 0
I2 + xm – ym ≤ 520
2 900xm – C2 ≤ 0
ym – I2 ≤ 0
I2 + xm – ym = 200
Con todas las variables mayores o iguales a cero.
102
Formulación de problemas de programación lineal
Al resolver este problema utilizando la herramienta Solver de Excel, se obtiene que
el plan óptimo de compras y ventas es éste:
Comprar:
Vender:
520 t en enero
200 t en marzo
100 t en enero
520 t en febrero
Al finalizar marzo se dispondrá de 200 toneladas de maíz en la bodega y de
$1 938 000 en caja.
Lecturas complementarias
Eppen y otros (2000), sobre todo el capítulo 3, secciones 3.1 a 3.4 y 3.10 a 3.17;
Arreola y Arreola (2003), capítulo 2; Stokey y Zeckhauser (1978).
Problemas de la unidad 3
Para cada uno de los problemas de esta sección, identifique las variables con las unidades que corresponda, defina la fo, identifique las restricciones y plantee las ecuaciones
del modelo de pl.
Problemas de producción
Problema 3.1
Una fábrica de productos metal-mecánicos tiene alguna capacidad excedente que quiere utilizar para la producción de algunos de los tres nuevos artículos que está considerando. El tiempo disponible medido en horas-máquina a la semana es el siguiente: para
la fresadora 500 horas, torno, 350 horas, y rectificadora, 150 horas.
La productividad de cada máquina, esto es, el número de productos que hace cada
máquina en una hora, para cada uno de los tres productos es la siguiente:
103
Programación lineal
Cuadro 3.12
Máquina
Prod. 1
Prod. 2
Prod. 3
Fresadora
9
3
5
Torno
5
4
0
Rectificadora
3
0
2
El departamento de mercadotecnia estima que se podrá vender todo lo que se produzca de los producto 1 y 2, mientras que del producto 3 la demanda semanal no supera las 20 unidades. Si la ganancia unitaria es de $50, $20 y $25, respectivamente,
¿cuál debe ser la combinación de productos que maximice la ganancia semanal?
Problema 3.2
En una planta se producen cuatro productos diferentes (a, b, c, d); para cada producto
se requiere realizar trabajo con cuatro máquinas (cortar, armar, pegar y pintar), el cual
se expresa en min/kg en el cuadro 3.13. Se cuenta con 60 horas semanales de cada máquina (el armado se realiza con una máquina robotizada totalmente).
Cuadro 3.13
Máquina min/kg
Cortadora
Robot
Pegadora
Compresora
Demanda máxima
a
5
10
6
3
400
b
3
6
4
8
100
c
4
5
3
3
150
d
4
2
1
2
500
Los precios de venta de los productos por kilogramo son $9, $7, $6 y $5, respectivamente; la mano de obra tiene un costo de $2 por hora. El costo de materia prima para el
producto 1 es de 3.5 $/kg, mientras que para los otros es de 1.2 $/kg. ¿Cuál es la producción semanal que más le conviene para maximizar su utilidad?
Problema 3.3
Una planta productora de fibras tiene una línea donde produce poliéster, elastano y
dacrón. El departamento de hilandería requiere de 20, 40 y 30 horas respectivamente para producir una tonelada de cada una de las fibras; este departamento cuenta
104
Formulación de problemas de programación lineal
con 2 000 horas. El departamento de teñido cuenta con 4 800 horas y requiere 70,
80 y 90 horas respectivamente para teñir una tonelada de fibra. Por último los productos deben ser colocados en bobinas de 1 kg para su venta. El tiempo requerido es
de 25 horas por cada tonelada de poliéster o de dacrón y de 35 horas para bobinar
una tonelada de elastano pues debe realizarse mucho más lentamente para no perder
sus propiedades. Se cuenta con 1 500 horas de bobinadora. Las ventas limitan la producción de dacrón a 25 000 kg por mes. Si los costos de materia prima para las
3 fibras son similares y si el precio de venta es de 1 000, 1 500 y 2 000 pesos por tonelada, plantéelo como un problema de pl.
Problema 3.4
Una cooperativa opera cuatro granjas con rendimientos similares. Cada una de las
granjas tiene cierta cantidad de hectáreas y horas hombre disponibles como se muestra
en el cuadro 3.14:
Cuadro 3.14
Granja
ha útiles
Horas disponibles al mes
1
500
1 700
2
900
3 000
3
300
900
4
700
2 200
Se está pensando en sembrar tres cultivos: maíz, frijol y calabaza, cada uno de los
cuales produce distintas ganancias y requieren distinta cantidad de mano de obra (véase cuadro 3.15). También por cuestiones de dinero, solamente se compraron las semillas y fertilizantes para determinado número de ha máximo de cada cultivo.
Cuadro 3.15
Semillas y fertilizantes
ha máximas
Horas mes/ha
Ganancias esperadas
por ha ($)
Maíz
700
2
500
Frijol
800
4
200
Calabaza
300
3
300
Cultivo
Determine el plan de cultivo más apropiado con los recursos disponibles.
105
Programación lineal
Problema 3.5
Una cooperativa agrícola posee 3 ranchos de 25, 30 y 40 ha respectivamente. Se está
planeando la producción del próximo ciclo agrícola. Las opciones son sembrar maíz,
frijol y sorgo; además tienen instalaciones para la cría de hasta 2 500 pollos en el rancho
más grande (además de las hectáreas para cultivo). Cuentan con un capital de $200 000
para gastos de fertilizantes, semillas y el alimento de las aves. Debido a la cantidad de
agua disponible en la presa, se les han asignado 200 000 m3 para el riego.
Para la cría de pollos se requieren de $20 por pollo, y un hombre puede atender a
250 animales (durante 125 días, que es el periodo antes de venderlos). Las necesidades
de agua son inferiores a 1 m3 diario (puede despreciarse), y la utilidad, el precio de venta menos los costos, es de $20 por ave. En el siguiente cuadro se presentan los datos
específicos de cada rancho así como los requerimientos de mano de obra por hectárea
y la lámina de agua de cada cultivo para todo el ciclo productivo.
Cuadro 3.16
Mano
de obra
(h/ha)
Costo de los
insumos
($/ha)
Lámina
de agua
(cm)
Utilidad
($/ha)
Rancho
Mano de obra
disponible
(h)
Maíz
800
3 000
55
7 000
1
12 000
Frijol
1 200
5 000
60
10 200
2
20 000
Sorgo
300
1 200
20
4 500
3
27 000
La cooperativa debe planear cuántas hectáreas de cada cultivo sembrar y dónde, así
como la conveniencia o no de criar pollos. Para alimentar a los pollos requiere sembrar
al menos 3 ha de sorgo.
a) ¿Cuántas variables de decisión tiene este problema?, descríbalas.
b) ¿Cuántas restricciones tiene el problema y cuáles son?
c) Plantee el problema como un modelo de pl (sistema de ecuaciones).
Problema 3.63
Una ciudad de dos millones de habitantes, que produce 3 000 toneladas de residuos
por día, utiliza 3 incineradores, bastante obsoletos por cierto, como el método para
procesar la mayor parte de sus residuos. El resto los envía a un relleno sanitario a 20 km
de la ciudad, con un costo mucho más elevado.
3 Problema de políticas públicas tomado de Stokey y Zeckhauser (1978).
106
Formulación de problemas de programación lineal
La capacidad en toneladas de cada incinerador así como las unidades de los contaminantes bióxido de sulfuro y de partículas enviadas a la atmósfera por tonelada incinerada son:
Cuadro 3.17
Incinerador
Capacidad (t/día)
Emisiones so2 (Und/t)
Partículas (kg/t)
1
1 200
250
20
2
800
150
30
3
1 000
220
24
La nueva reglamentación para el control de emisiones indica que las plantas de incineración tendrán como topes en la emisión de contaminantes hasta 50 000 kg de
partículas suspendidas y no más de 400 000 unidades de bióxido de sulfuro.
La ciudad debe planear la manera más económica de procesar sus desperdicios sin
exceder los topes estipulados por la nueva reglamentación ambiental.4 Plantee el problema como un modelo de pl.
Problema 3.75
Una empresa pública generadora de energía tiene una demanda de 2 000 megavatios
por hora (MWh) para una ciudad industrial. La legislación ambiental la obliga a que la
emisión de contaminantes generada esté por debajo de 180 kg/h. La empresa debe decidir qué combustibles y método utilizar para minimizar los costos de generación, pero
cumpliendo con las reglamentaciones ambientales.
Cuadro 3.18
Contaminantes
Costo mwh
Combustible y método actual
0.12 kg/ MWh
$3.5
Diesel pesado
0.04 kg/ MWh
$5.0
Con filtros de pila
0.021 kg/ MWh
$5.8
Importar energía
0
$4.5
Pero si solamente puede importar 200 MWh, ¿qué deberá hacer?
4 La incineración de los desperdicios se realiza solamente en sociedades altamente industrializadas,
que además realizan la separación de los materiales reutilizables, y los residuos remanentes tienen un elevado
potencial calorífico.
5 Problema elaborado por la maestra Myriam Cardozo.
107
Programación lineal
Problema 3.8
Una refinería compra dos tipos de petróleo: ligero tipo Brent y petróleo crudo pesado
tipo Maya. Los costos actuales están en 77 y 64 dólares por barril, respectivamente. De
cada tipo de petróleo se obtiene por el proceso de destilación las siguientes cantidades
de gasolina, diesel y aceites lubricantes, expresado en barriles:
Cuadro 3.19
Gasolina
Diesel
Aceites
Crudo ligero Brent
0.40
0.25
0.30
Crudo pesado Maya
0.33
0.38
0.25
La refinería debe entregar mensualmente 600 000 barriles de gasolina, 500 000 barriles de diesel y 200 000 barriles de aceites lubricantes. Encuentre la cantidad de barriles de crudo de cada tipo que le conviene comprar para satisfacer la demanda con el
mínimo costo en los insumos.
Problemas de planeación financiera
Problema 3.9
Un asesor financiero debe colocar 10 millones de pesos en cuatro alternativas financieras, cuidando obtener el mayor rendimiento anual, pero manteniendo al menos
10% de liquidez. Las opciones son Cetes a 90 días, Cetes a 180 días, acciones de
Cemex y mesas de dinero. El rendimiento esperado es de 7.25% y 7.45% para los
Cetes; Cemex se espera que de 8.5% a condición de retenerlas durante un año; y en
mesas de dinero se espera 6.25%. Para minimizar riesgos no se quiere tener más del
50% ni en acciones de Cemex ni en Cetes. Las acciones de Cemex cuestan $17, y
los Cetes se venden en unidades de $1 000. Plantee el problema como un modelo
de pl.
Problema 3.10
Banco Azteca estima que el próximo año tendrá 100 millónes de pesos para préstamos.
Tiene distintos tipos de préstamos a diferente tasa de interés.
Debido a las políticas de la empresa se deben respetar los siguientes límites: a) los
préstamos personales no pueden exceder 15%. b) Los préstamos para mejora de casas
108
Formulación de problemas de programación lineal
junto con los dedicados a actividades recreativas no pueden exceder 20% del total de
los créditos. c) Los prestamos a las Pymes deben ser menos de 30% del total. d) Al menos 10% de los préstamos deben destinarse a los préstamos personales tipo a, otro
tanto debe destinarse a las hipotecas y a las Pymes. El banco quiere maximizar sus utilidades. ¿Cuántas variables tiene el problema?; ¿cuántas restricciones? Plantee el problema de pl.
Cuadro 3.20
Tipo de préstamo
Interés anual (%)
Tipo de préstamo
Interés anual (%)
Personal tipo a
8
Mejoras a la casa habitación
10
Personal tipo b
12
12
Automóvil
10
Implementos para
actividades recreativas
Hipoteca
8
Pymes
9
Problema 3.116
Conacyt ha decidido repartir 1 000 millones de pesos para estimular la investigación en
innovación tecnológica en el área de energía. Se recibieron 200 solicitudes para otros
tantos proyectos entre los cuales se seleccionaron 6 finalistas. Un grupo de científicos y
economistas evaluaron los proyectos y estimaron los beneficios potenciales que cada
uno de ellos podría significar para un periodo de 10 años por cada peso invertido ahora en investigación. Los proyectos seleccionados aparecen en el cuadro 3.21.
Cuadro 3.21
Proyecto
Tipo de energía
Beneficio neto
por peso invertido
Fondos solicitados
(millones de pesos)
1
Solar
4.4
220
2
Solar
3.8
180
3
Biocombustible
4.1
250
4
Carbón
3.5
150
5
Nuclear
5.1
400
6
Geocéntrica
3.2
120
Esto quiere decir que el primer proyecto al cabo de 10 años potencialmente producirá $4.4 por cada peso que se haya invertido en él después de recuperar la inversión, y
6 Problema adaptado de un ejercicio de Reyes García y Romero (2004).
109
Programación lineal
que requiere como máximo 220 millones de pesos, pero el Conacyt puede decidir entregarle sólo parte de esos fondos.
El Conacyt necesita decidir cuánto dinero asignar a cada proyecto tratando de
maximizar los beneficios futuros, pero también deben tomarse en cuenta otros criterios
por lo que se ha decidido que al menos deben otorgarse $300 millones para la investigación de energía solar, no menos de 100 millones de pesos para biocombustibles y
restringir la cantidad invertida en investigaciones relacionadas con carbón y nuclear a
menos de 250 millones de pesos en total.
Planeación de publicidad
Problema 3.12
Se está planeando una campaña publicitaria para anunciar la apertura de un nuevo supermercado en Tapachula. Se cuenta con un presupuesto de $250 000 y se está considerando la posibilidad de contratar anuncios en la radio a $10 000, y en la televisión
local, a $20 000. Cada anuncio en la radio llega a 12 000 personas y cada anuncio en la
televisión llega a 20 000 personas. Se quiere llegar a la mayor cantidad de público posible, pero garantizando una audiencia de al menos 20 000 mujeres y de 18 000 hombres
adultos. Los medios de difusión dicen que su audiencia por anuncio es:
Cuadro 3.22
Mujeres
Hombres
Radio
2 000
1 500
Televisión
2 500
5 000
Problemas de dietas
Problema 3.13
Un criadero de cerdos debe determinar los distintos tipos de alimento que deben dar a
los cerdos para cubrir los requerimientos nutricionales a costo mínimo. En el siguiente
cuadro se dan las unidades nutricionales por kilogramo de alimento, los requerimientos mínimos y los costos. Se debe encontrar la dieta de costo mínimo.
110
Formulación de problemas de programación lineal
Cuadro 3.23
Maíz (kg)
Grasa (kg)
Alfalfa (kg)
Requisito
mínimo
Unidad
Carbohidratos
90
20
40
200
g
Proteínas
30
80
60
180
g
Vitaminas
10
20
60
150
mg
Costo($/kg)
8
9
6
Problema 3.14
Un hospital se propone elaborar una dieta balanceada para el desayuno de sus pacientes
con las siguientes características:
a)El desayuno debe aportar no menos de 480 calorías
b) El consumo mínimo de proteínas en el desayuno debe ser de 25 g.
c) Los alimentos que se han de utilizar son jamón, huevo, leche, pan y queso fresco;
Las características de cada uno de estos alimentos se dan a continuación:
Cuadro 3.24
Alimentos
Porción
Precio
Calorías
Proteínas (g)
Jamón
1 rebanada
$2.5
76
3.9
Huevo
1 pieza
$1.0
74
5.6
Leche
1 vaso
$2.2
116
6.8
Pan
1 pieza
$0.5
124
2.0
Queso
1 ración
$4.0
127
11.3
Plantéelo como un modelo de pl considerando que el desayuno no debe llevar más
de dos huevos y que sólo se incluirá una pieza de pan si se incluye una porción de jamón.
111
Programación lineal
Problemas de mezclas
Problema 3.15
Una fábrica de plásticos planea sacar un nuevo producto utilizando plástico reciclado
proveniente de cuatro plantas recicladoras. Dadas las características del producto que
se quiere obtener en cuanto a flexibilidad, transparencia y resistencia térmica, se tiene
que encontrar la mezcla más conveniente de los cuatro insumos de tal manera que la
resina resultante contenga al menos 20% de pet, al menos 30% de polietileno de
baja densidad y al menos 20% de polipropileno. Debido a que se necesita que el producto final sea muy flexible, no debe contener más de 30% de pet ni más de 35% de
polietileno.
En el siguiente cuadro se indica el porcentaje del contenido de cada una de las resinas en los insumos provenientes de las cuatro plantas:
Cuadro 3.25
Insumos
de resina
Planta 1
Planta 2
Planta 3
Planta 4
pet
35
25
25
30
Polietileno
45
15
30
25
Polipropileno
12
60
40
25
El precio del kilogramo de cada uno de los insumos es de $20, $25, $15 y $10. Indique cuál es la mezcla de insumos más conveniente para minimizar el costo del producto.
Problema 3.16
Una pequeña fábrica de productos cosméticos naturales produce jabón, champú para
prevenir la caída del cabello, crema y aceite para la piel. Sus ingredientes básicos son la
jojoba, el romero y la sábila que ellos mismos producen. Esta temporada han cosechado
y procesado 1 000 litros de sábila, 560 litros de aceite de romero y 2 200 litros de aceite de jojoba. Debido a que se trata de una cooperativa quieren utilizar especialmente
todo lo producido por ellos mismos.
En el siguiente cuadro se indican las cantidades mínimas y máximas que debe contener un litro de estos productos, así como los precios tentativos de venta por litro. El
jabón lleva una pasta base que no debe exceder 70%; el champú puede tener hasta 20%
de agua, la crema sólo 12% y el aceite apenas 5%. Se debe decidir cuál es el mejor plan
de producción.
112
Formulación de problemas de programación lineal
Cuadro 3.26
Jojoba (ml)
Sábila (ml)
máx. 180
máx. 300
mín. 125
mín. 175
Champú
máx. 250
máx. 350
mín. 140
mín. 220
mín. 320
Crema
máx. 450
mín. 220
máx. 30
55
mín. 50
máx. 100
70
Jabón
Romero (ml)
Precio de venta ($/l)
25
máx. 350
43
mín. 300
Aceite
máx. 800
mín. 700
mín. 30
Turnos de trabajo
Problema 3.17
Un municipio conurbado altamente poblado ha estimado el número mínimo de patrullas necesarias para la vigilancia de su territorio para periodos de cuatro horas. Los oficiales de las patrullas trabajan turnos continuos de ocho horas y no hay policías con
turnos parciales. Se quiere organizar los turnos para reducir el número de empleados
necesarios. Los oficiales pueden empezar su turno al comienzo de cualquiera de los intervalos que se muestran a continuación; en cada patrulla deben ir dos oficiales.
Cuadro 3.27
Intervalo
Número mínimo requerido
12 a 16
100
16 a 20
250
20 a 00
400
00 a 4
500
4a8
200
8 a 12
150
Indique cuál es la cantidad de patrullas con que debe contar el municipio (se considera que debe tener un 10% de carros extra para darles mantenimiento) y cuántos
oficiales requiere para satisfacer la demanda de vigilancia.
113
Programación lineal
Problemas de transporte
Problema 3.18
Una compañía que produce concreto debe abastecer a cuatro obras en construcción. La
compañía tiene tres plantas desde las que suministrar el concreto. En el cuadro se indican los costos por camión enviado desde las plantas a las obras, que depende de la distancia que se debe recorrer, así como la capacidad diaria en cargas de camión de cada
planta y la demanda de cada obra.
Cuadro 3.28
Obra 1
Obra 2
Obra 3
Obra 4
Capacidad de
las plantas
1
$80
$100
$60
$70
120
2
$40
$80
$75
$60
100
3
$100
$120
$90
$110
80
50
40
75
60
Planta
Demanda
Plantee las ecuaciones como un problema de pl.
Problema 3.19
Una compañía tiene dos bodegas que surten mercancía a cinco tiendas de abarrotes.
Los envíos se hacen sólo por una carga completa de camión. El número de cargas requerido por cada tienda es de 80, 50, 75, 45, 80, respectivamente. Los costos de envío
están en el siguiente cuadro junto con las cargas disponibles en cada bodega.
Cuadro 3.29
Tiendas
1
2
3
4
5
Máx. de cargas
disponibles
Bodega 1
$40
$50
$45
$50
$25
100
Bodega 2
$50
$35
$40
$20
$40
250
a) Haga una representación del problema.
b) Plantee las ecuaciones del problema.
c) Dé una solución posible.
114
Formulación de problemas de programación lineal
Problema 3.20
Una empresa dueña de una cadena de supermercados acaba de comprar las tiendas de
otra cadena, con lo que logra una cobertura a nivel nacional. Ahora tiene que diseñar
la estrategia para surtir a sus nuevas tiendas desde las bodegas que tenía establecidas,
incluso para determinar cuáles de ellas necesitarán aumentar su capacidad. El criterio
para decidir desde dónde surtir a las nuevas tiendas lo establece tratando de minimizar
las distancias, ya que esto se traduce en disminución de combustible y de costos. Tiene
que proveer de mercancías a cuatro tiendas, una en Cuernavaca, otra en Puebla y dos
en el Distrito Federal, una al norte y otra en el oriente. Las bodegas se encuentran en
la ciudad de Veracruz, en Puebla y Toluca. En el siguiente cuadro se dan las distancias
en kilómetros entre las bodegas, las tiendas y las necesidades semanales medidas en camiones de 12 t.
Cuadro 3.30
Tiendas/Bodegas
Toluca
Puebla
Veracruz
Necesidades semanales
Cuernavaca
96
109
291
35
D. F. norte
40
80
260
70
D. F. oriente
48
75
255
73
Puebla
117
8
182
47
La bodega de Toluca tiene capacidad para surtir 48 toneladas, la de Puebla, un
máximo de 72, y la de Veracruz puede suplir hasta 150, y lo que no sea necesario se
embarcará para Tampico. Encuentre la mejor manera de realizar el transporte de
mercancías.
Problema 3.217
Se debe realizar un plan de emergencia para asignar heridos a los hospitales generales
de la zona en caso de que ocurra un temblor importante en la ciudad. Debido a la densidad de la población y al tipo de construcciones, se estima que un temblor de grado 6
en la escala de Richter produciría 300 heridos en la zona a y 250 heridos en la zona b.
Hay tres hospitales en la ciudad para atender este tipo de emergencias. El tiempo de
traslado desde el lugar a es de 25, 15 y 10 minutos a cada uno de los hospitales, y desde el punto b es de 20, 5 y 15 minutos. Las capacidades de los hospitales para estos
casos son 250, 150 y 150 pacientes respectivamente. ¿Cómo convendría asignar las
7 Problema de políticas públicas elaborado a partir de Stokey y Zeckhauser (1978).
115
Programación lineal
víctimas a los hospitales? ¿Cuál es el tiempo promedio de traslado? Si disponen de 10
ambulancias, ¿cuánto tiempo tardarán en recoger todos los heridos?
Problema 3.22
Una cadena de restaurantes tiene tres locales en Tlalpan, Villa Coapa y Tláhuac, a los
que debe surtir los vasos desechables. Hay tres proveedores con diferentes precios y
capacidades de producción que le ofrecen el producto. Éstos le enviaron sus cotizaciones y capacidades de producción. Además se anexa el precio del transporte por 1 000
unidades. Se solicita plantearlo como un problema de transporte.
Cuadro 3.31
Proveedor
Precio (por 1 000 unidades)
Capacidad anual
a
$9
40 000
b
$10
75 000
c
$11
135 000
Costo del transporte por 1 000 vasos en pesos.
Cuadro 3.32
De proveedor
Tlalpan
Villa Coapa
Tláhuac
a
8
1
3
b
5
2
5
c
2
4
2
Se necesitan 90 000 vasos en Tlalpan; 70 000 en Villa Coapa, y 90 000 en Tláhuac.
Problemas de inventarios
Problema 3.238
Una compañía quiere planear la producción de cierto artículo para las próximas 4 semanas. El costo de producción es de $1 000 las 2 primeras semanas y $1 500 las siguientes. Las demandas semanales son 7, 8, 10 y 10 unidades, pero la planta no puede
8 Este
problema fue adaptado de Moskowitz, H. Y. Wrigth, G., Investigación de operaciones, PHH.
116
Formulación de problemas de programación lineal
producir más de 9 unidades semanales, aunque puede pagar horas extra las dos últimas
semanas, lo que le permite aumentar la producción en 2 unidades semanales, con un
costo extra de $580 por unidad. El exceso de producción se puede almacenar a un costo de $35 por semana y por unidad. El objetivo es minimizar los costos totales.
Respuesta a los problemas de la unidad 3
Problema 3.1. El problema tiene 3 variables y 4 restricciones. La solución óptima es
producir a la semana 450 unidades del artículo 1; 1 040, del artículo 2, y no producir el tercer artículo. La ganancia semanal será de $43 300 y quedarán sin utilizar
103.3 horas de fresadora.
Problema 3.2. La solución óptima es producir de a, 220 kg; b, 100 kg; c, 150 kg, y d,
525 kg. Con esta producción sobrarían (1 505 min), 25 h de pegadora y 15.7 h de
compresora. La utilidad sería de $3 556.50.
Problema 3.3. Se deben producir 25 t de elastano y 25 t de dacrón, con lo que se obtiene una utilidad de $87 500, quedarán disponibles 250 h en el departamento de
teñido.
Problema 3.4. La cooperativa deberá sembrar:
granja 1: 200 ha de frijol y 300 ha de calabaza,
granja 2: 300 ha de maíz y 600 ha de frijol,
granja 3: 300 ha de maíz,
granja 4: 100 ha de maíz.
La ganancia esperada con este plan de producción es de $600 000.
Problema 3.5. a) Hay 10 variables de decisión: el número de ha que se deben sembrar
de cada cultivo en cada rancho y el número de pollos que deben criarse. b) El problema tiene 10 restricciones. c) La solución óptima será criar los 2 500 pollos para
los que hay capacidad, y producir especialmente sorgo: 25 ha en el rancho 1, 27.5
ha en el rancho 2, y 40 ha en el rancho 3; además se deberán sembrar 2.5 ha en el
rancho 2 de frijol. La utilidad será de $491 750. Seguramente hay otras soluciones
alternas con igual utilidad.
Problema 3.6. Solamente se podrán incinerar 1 987.5 t: en el incinerador 1, 625 t; en
el incinerador 2, 800 t, y en el incinerador 3, 562.5 t. Las otras 1 012.5 t deberán
ser enviadas al relleno sanitario para no sobrepasar los límites de contaminación
establecidos por la norma ambiental.
Problema 3.7. La empresa pública deberá producir 1 350 MWh con el combustible y
métodos tradicionales, 450 mwh a partir de diesel pesado e importar los 200 mwh
que le permiten. El costo será de $7 875 pesos por los 2 000 mwh necesarios.
Problema 3.8. La refinería debe comprar 906 475 barriles de petróleo ligero y 719 424
barriles de crudo pesado con un costo de $115 841 727 millones de dólares. Con
117
Programación lineal
esto producirá exactamente las cantidades necesarias de gasolina y diesel, pero tendrá un excedente de 215 798 barriles de aceites lubricantes.
Problema 3.9. El asesor debe invertir $1 000 000 en mesas de dinero; $4 000 000 en
4 000 Cetes a 180 días, y $5 000 000 en 249 117 acciones de Cemex. El rendimiento será de $785 500.
Problema 3.10. El banco, para maximizar sus utilidades, debe prestar:
10% a préstamos personales tipo a
5% a préstamos personales tipo b
20% a préstamos para actividades recreativas
10% a préstamos hipotecarios
45% a préstamos para automóviles (o a mejora de vivienda)
10% en préstamos a Pymes
Problema 3.11. El Conacyt ha decidido entregar las siguientes cantidades a cada uno
de los proyectos, expresado en millones de pesos:
Solar 1:
220 mp
Solar 2:
180 mp
Biocombustibles:
250 mp
Nuclear:
250 mp
Geotérmica:
100 mp
Problema 3.12. Es conviente contratar 25 anuncios de radio solamente, con lo que se
tendría una audiencia de 300 000 personas con al menos 50 000 mujeres y 37 500
hombres.
Problema 3.13. La dieta de costo mínimo es de $24 diarios por cerdo e incluye 1.20 kg
de maíz, 0.103 kg de grasa y 2.27 kg de alfalfa; si se quiere que los animales engorden más rápido se les puede dar comida suplementaria.
Problema 3.14. La dieta de costo mínimo debe incluir una rebanada de jamón, dos
huevos, 1.2 vasos de leche (o sea, un vaso grande) y una pieza de pan. El costo del
desayuno es de $7.55 aproximadamente.
Problema 3.15. La mezcla más conveniente tiene un costo de 13 $/kg y está compuesta con 20% de la planta 1; 20% de la planta 3, 60% de la planta 4.
Problema 3.16. La fábrica debe producir solamente champú, crema y aceite. Las mezclas que se deben realizar se muestran en el cuadro con una utilidad de 258 434
pesos.
118
Formulación de problemas de programación lineal
Cuadro 3.33
Litros
Champú
Crema
Aceite
Jojoba
107.8
193.4
1 899.0
Sábila
238.6
354.5
407.0
Romero
269.4
19.3
271.3
Agua
154.0
77.3
135.6
Total
769.8
644.5
2 715.9
Problema 3.17. Se debe contar con no menos de 500 patrullas (sería conveniente tener
algunas para imprevistos y mantenimiento); se deben organizar 900 parejas de oficiales, o sea, 1 800 oficiales. Aunque hay muchas soluciones, una posible sería que
entren a trabajar 150 oficiales a las 12 am, 350 a las 4 pm, 550 a las 8 pm, 450 a las
12 am y 300 a las 8 am.
Problema 3.18. La compañía debe enviar la carga en los camiones como se indica en el
cuadro, y el costo será de $13 950.
Cuadro 3.34
Obra 1
Obra 2
Planta 1
Planta 2
50
Obra 3
Obra 4
70
50
40
10
Planta 3
5
Problema 3.19. En este caso la oferta es inferior a la demanda, por lo que se sugiere para
minimizar los costos, enviar la siguiente cantidad de cargas:
Cuadro 3.35
Bodega
Tienda 1
1
20
2
60
Tienda 2
Tienda 3
Tienda 4
Tienda 5
80
50
75
45
Problema 3.20. Para surtir la demanda recorriendo la menor distancia posible se deben
realizar los siguientes envíos de camiones. Se recorrerán 31 964 km.
119
Programación lineal
Cuadro 3.36
Distrito Federal
(zona norte)
Toluca
Cuernavaca
37
35
Puebla
48
Puebla
Veracruz
Distrito Federal
(zona oeste)
22
36
47
Problema 3.21. Lo más conveniente es enviar de la zona a 150 heridos al hospital 1 y
150 al hospital 3. De la zona b se deben enviar 100 heridos al hospital 1 y 150 al
hospital 2. El tiempo promedio de los traslados será de 14.55 minutos. Como las
ambulancias deben ir y regresar, demorarán más de 26 horas (26.66) en terminar de
trasladar a todos los heridos.
Problema 3.22. Lo más conveniente para la cadena es surtir al restaurante de Tláhuac
con 40 000 unidades del proveedor a, 5 000 de b y 45 000 de c. Para el restaurante
de Villa Coapa se deben comprar las 70 000 piezas al proveedor b; y para Tlalpan,
las 90 000 unidades del proveedor c. El costo será de $3 150.
Problema 3.23. La mejor solución para la compañía es producir lo siguiente:
Primer semana: 9 unidades, 7 para la demanda y 2 para la tercera semana
Segunda semana: 9 unidades, 8 para la demanda y una para la cuarta semana
Tercera semana: 8 unidades
Cuarta semana: 9 unidades
Con un costo de 18 (1 000) + 2 (2) 35 + 1 (35) + 17 (1 500)
120