www.klasesdematematicasymas.com
Anuncio

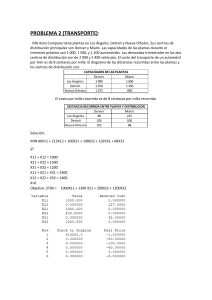
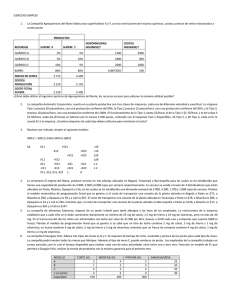
Preparado por: Oscar Restrepo 1. Resolver el siguiente problema por el sistema dual simplex Max Z = 0,50X1 + 0,40X2 Sujeto a 2X1 + X2 ≤ 120 2X1 + 3X2 ≤ 240 X1, X2 ≥0 El modelo estándar es: Z – 0,5X1 – 0,40X2 + 0S1 + 0S2 = 0 2X1 + X2 + S1 = 120 2X1 + 3X2 + S2 = 240 X2 -0,4 1 3 S1 0 1 0 S2 0 0 1 Z X1 S2 z 1 0 0 X1 0 1 0 X2 -3/20 1/2 2 S1 1/4 1/2 -1 Z X1 X2 z 1 0 0 X1 0 1 0 X2 0 0 1 bi 0 120 240 .c X1 -0,5 2 2 as z 1 0 0 bi 30 60 120 S2 3/40 -1/4 1/2 bi 39 30 60 em at ic a S2 0 0 1 em at S1 7/40 3/4 -1/2 se sd sy m Z S1 S2 om Como la función objetivo se debe maximizar no se multiplica por (-1). Además como las restricciones son menor o igual entonces nos quedan de la misma forma. Ya podemos desarrollar el tablero simplex w .k la El tablero es óptimo por tanto X1 = 30, X2= 60, S1 = 0, S2 = 0, Z = 39 w w 2. Una Fábrica de automóviles, produce dos tipos de auto por pedido, lujo y corriente, usando hierro, acero de alta calidad y plástico de alta resistencia, en unidades cuadradas con el mismo espesor, a saber para el auto de lujo se necesitan 1000 unidades cuadradas de hierro, 400 de acero y 1500 de plástico, para un automóvil corriente se requieren 1000 unidades de hierro, 1600 de Acero y 2000 de plástico. Los automóviles de lujo producen por su venta una ganancia de $12000, los tipo corriente $9000. En la actualidad, la empresa dispone de 200000 unidades de hierro, 128000 de Acero y 220000 de Plástico. Han recibido pedidos para dos tipos de autos, y les gustaría producir la cantidad de automóviles de cada tipo que maximicen la utilidad. ¿Cuántos automóviles de cada tipo se deben producir? Asumimos que X1 es el número de autos de tipo de lujo X2 es el número de autos de tipo corriente www.klasesdematematicasymas.com Preparado por: Oscar Restrepo Función Objetivo: Maximizar utilidades Z = 12000X1 + 9000X2 Sujeto a 1000X1 + 1000X2 ≤ 200000 400X1 + 1600X2 ≤ 128000 1500X1 + 2000X2 ≤ 220000 X1, X2 ≥0 Restricción para el hierro Restricción para el acero Restricción para el plástico Modelo estándar Z – 12000X1 – 9000X2 + 0S1 + 0S2 + 0S3 = 0 1000X1 + 1000X2 + S1 = 200000 400X1 + 1600X2 + S2 = 128000 1500X1 + 2000X2 + S3 = 220000 X2 7000 -1000/3 3200/3 4/3 S1 0 1 0 0 S2 0 0 1 0 em S3 8 -2/3 -4/15 1/1500 bi 1760000 160000/3 208000/3 440/3 em at bi 0 200000 128000 220000 om X1 0 0 0 1 S3 0 0 0 1 .c z 1 0 0 0 as Z S1 S2 X1 S2 0 0 1 0 m S1 0 1 0 0 sy X2 -9000 1000 1600 2000 ic a X1 -12000 1000 400 1500 at Z S1 S2 S3 z 1 0 0 0 sd El tablero es óptimo por tanto la solución es: .k la se X1 = 440/3, X2= 0, S1 = 160000/3, S2 = 208000/3, S3 = 0, Z = 1760000 w w w 3. Una fábrica de muebles construye mesas y sillas, en diversos estilos. Cada mesa, independientemente de su estilo, se vende a $4 y cada silla a $3. Las restricciones de tiempo a la semana en la actualidad para estos productos están dados por 2X1 + X2 ≤ 30 y X1 + 2X2 ≤ 24 y la empresa decide cambiar el tiempo disponible para estos productos a 35 horas y 30 horas, respectivamente, ¿Cuál sería el efecto de este cambio? ¿Cuál la maximización de las utilidades? Función Objetivo: Maximizar utilidades Z = 4X1 + 3X2 Sujeto a 2X1 + X2 ≤ 30 X1 + 2X2 ≤ 24 X1, X2 ≥0 Modelo estándar Z – 4X1 – 3X2 + 0S1 + 0S2 = 0 2X1 + X2 + S1 = 30 X1 + 2X2 + S2 = 24 www.klasesdematematicasymas.com Preparado por: Oscar Restrepo Z S1 S2 z 1 0 0 X1 -4 2 1 X2 -3 1 2 S1 0 1 0 S2 0 0 1 bi 0 30 24 Z X1 S2 z 1 0 0 X1 0 1 0 X2 -1 ½ 3/2 S1 2 ½ -1/2 S2 0 0 1 bi 60 15 9 Z X1 X2 z 1 0 0 X1 0 1 0 X2 0 0 1 S1 5/3 2/3 -1/3 S2 2/3 -1/3 2/3 bi 66 12 6 om El tablero ya es óptimo. Por tanto, la solución es: as .c X1 = 12, X2= 6, S1 = 0, S2 = 0, Z = 66 em at ic a sy m Si las restricciones cambian a 35 y 30, el modelo queda Función Objetivo: Maximizar utilidades Z = 4X1 + 3X2 Sujeto a 2X1 + X2 ≤ 35 X1 + 2X2 ≤ 30 X1, X2 ≥0 em at La matriz inversa óptima es: ⁄ ⁄ ⁄ ⁄ ) ( ) ⁄ ( ⁄ w w w .k la se sd ( ⁄ ⁄ )( ) ( ⁄ ⁄ ) El nuevo valor de la función objetivo es: ⁄ ⁄ ⁄ 4. Una cadena de tres almacenes en el país, los cuales usan pocillos porcelanizados. Se ha invitado a tres proveedores para compartir por la concesión de surtir estos productos. Sus propuestas son: Proveedor A B C Precio $90 $100 $110 Capacidad anual 30000 75000 135000 El costo de transporte por unidad está dado por www.klasesdematematicasymas.com Preparado por: Oscar Restrepo De A B C No 1 $80 $50 $20 No 2 $10 $20 $40 No 3 $30 $50 $20 Las necesidades de pocillos para los restaurantes son de 30000, 60000 y 15000 respectivamente. ¿Cuántos pocillos deben comprarse de cada proveedor para cada restaurante? La matriz de costos es: No-1 No-2 B C OFERTA 30 0 50 20 50 0 20 40 20 0 30000 60000 30000 75000 135000 15000 135000 240000 .c DEMANDA Ficticio 10 om A No-3 80 at em sd w w w .k la se Sujeto a Oferta X11+X12+ X13 ≤ 30000 X21+X22+ X23 ≤ 75000 X31+X32+ X33 ≤ 135000 Demanda X11+X21+ X31 ≥ 30000 X12+X22+ X32 ≥ 60000 X13+X23+ X33 ≥ 15000 Con Xij≥0, para i=1,23 j=1,2,3 em at ic a sy m as En este ejercicio cada proveedor tiene un precio de compra. Por tanto el modelo es el siguiente Si la variable Xij es lo que sale del proveedor i (A,B,C) a los restaurantes j (1,2,3) Minimizar Z= 90(X11+X12+ X13 ) + 100 (X21+X22+ X23 ) + 110(X31+X32+ X33 ) + (80X11+10X12+ 30X13 ) + (50X21+20X22+ 50X23 ) + (20X31+40X32+ 20X33 ) Solucionando el modelo a través de SOLVER se tiene X11= 0, X12= 30000, X13= 0, X21=0, X22=30000, X23=0, X31=30000, X32= 0 X33=15000 Con un costo de 12’450.000 5. Una empresa industrial tiene tres plantas de distribución, cuyo producto debe distribuirse a 4 almacenes. Las plantas 1, 2 y 3 producen 12, 17 y 11 pedidos por mes. Cada centro de distribución necesita recibir 12 pedidos por mes. El costo del flete de cada pedido es $200 más $1 por Km. ¿Cuánto se debería despachar a cada almacén para minimizar el costo del envío? Minimizar Z= (1000X11+1500X12+ 600X13 + 600X14) + (1300X21+1600X22+ 800X23 + 1200X24) + (800X31+1400X32+ 201X33 + 201X34) Sujeto a Oferta www.klasesdematematicasymas.com Preparado por: Oscar Restrepo X11+X12+ X13 + X14≤ 12 X21+X22+ X23 + X24≤ 17 X31+X32+ X33 + X34≤ 11 Demanda X11+X21+ X31 ≥ 12 X12+X22+ X32 ≥ 12 X13+X23+ X33 ≥ 12 X14+X24+ X34 ≥ 12 Con Xij≥0, para i=1,2,3 j=1,2,3,4 ic a sy m as .c om Para solucionarlo se utiliza WINQSB y se encuentra que: em at Es decir, X11= 11, X12= 0, X13= 0, X14 =0, X21=1, X22=4, X23=12, X24= 0 X31=0, X32= 0, X33=0, X34=11 Z = 31111 w w w .k la se sd em at 6. Una microempresa tiene 3 máquinas A, B y C y 3 operarios. El administrador de la empresa desea que los operarios trabajen en las tres máquinas, minimizando el tiempo total de trabajo. Cada operario debe ser asignado a una máquina y cada máquina debe ser ocupada por un operario. La siguiente tabla nos presenta la distribución de la información acerca del número de horas que pueden trabajar los operarios en una de las máquinas Horas Máquina Operario A B C 1 10 5 8 2 14 6 8 3 12 4 10 Utilizando el método húngaro se tiene A 10 14 12 1 2 3 1 2 3 Qi B 5 6 4 A 5 8 8 5 C 8 8 10 B 0 0 0 0 Pi 5 6 4 C 3 2 6 2 www.klasesdematematicasymas.com Preparado por: Oscar Restrepo 1 2 3 A 0 3 3 B 0 0 0 C 1 0 4 1 2 3 A 0 4 3 B 0 1 0 C 0 0 3 Por tanto la asignación queda de la siguiente manera Operario 1: Máquina A. Operario 2: Máquina C Operario 3: Máquina B sy m as .c om Costo: Z = 10 + 8 + 4 = 22 7. Una agencia de publicidad trata cuál de entre 4 ejecutivos de contabilidad Jaime, Lucía, Javier, Sonia debe asignarse a cada uno de los clientes mayores. Use el método conveniente para encontrar la solución óptima, a continuación se presentan los costos estimados de la asignación de cada ejecutivo ic a Jaime Lucía Javier Sonia 15 19 20 18 14 15 17 14 11 15 15 14 21 24 26 24 at em at A B C D sd se Jaime Lucía Javier Sonia Pi 15 19 20 18 15 14 15 17 14 14 11 15 15 14 11 21 24 26 24 21 w w w .k la A B C D em Usando el método húngaro A B C D Qi A B C D Qi Jaime Lucía Javier Sonia 0 4 5 3 0 1 3 0 0 4 4 3 0 3 5 3 0 1 3 0 Jaime Lucía Javier Sonia 0 3 2 3 0 0 0 0 0 3 1 3 0 2 2 3 www.klasesdematematicasymas.com Preparado por: Oscar Restrepo A B C D Jaime Lucía Javier Sonia 15 19 20 18 14 15 17 14 11 15 15 14 21 24 26 24 m as .c A B C D Jaime Lucía Javier Sonia 0 1 1 1 2 0 1 0 0 1 0 1 0 0 1 1 om Jaime Lucía Javier Sonia 0 2 1 2 1 0 0 0 0 2 0 2 0 1 1 2 A B C D Qi at ic a sy La asignación queda A: Jaime, B: Sonia, C: Javier, D: Lucía. Costo: Z = 15 + 14 + 15 + 24 = 68 la se sd em at em 8. Un corredor de bienes raíces planea la venta de cuatro lotes de terreno y ha recibido ofertas individuales de cuatro clientes. Debido a la cantidad de capital que se requiere, estas ofertas se han hecho en el entendimiento de que ninguno de los cuatro clientes comprará más de un lote, las ofertas se muestran en el cuadro siguiente, el corredor de bienes raíces quiere maximizar su ingreso total a partir de esas ofertas. Resolver el problema mediante el método húngaro. Establezca el valor de la función objetivo. w w w .k A B C D Julia 16 19 15 19 Teodoro Walter Sandra 15 25 19 17 24 15 15 18 10 0 15 17 Utilizando el método húngaro para maximizar Julia Teodoro Walter Sandra Pi A -16 -15 -25 -19 -25 B -19 -17 -24 -15 -24 C -15 -15 -18 -10 -18 D -19 0 -15 -17 -19 A B C D Julia 9 5 3 0 Teodoro Walter Sandra 10 0 6 7 0 9 3 0 8 19 4 2 www.klasesdematematicasymas.com Preparado por: Oscar Restrepo Julia 9 5 3 0 0 Teodoro Walter Sandra 10 0 6 7 0 9 3 0 8 19 4 2 3 0 2 A B C D Julia 9 5 3 0 Teodoro Walter Sandra 7 0 4 4 0 7 0 0 6 16 4 0 A B C D Julia 5 1 3 0 Teodoro Walter Sandra 3 0 0 0 0 3 0 4 6 16 4 0 A B C D Julia 5 1 3 0 Teodoro Walter Sandra 3 0 0 0 0 3 0 4 6 16 4 0 em at ic a sy m as .c om A B C D Qi em at Por tanto la asignación es: Lote A: Sandra, Lote B: Walter, Lote C: Teodoro, Lote D: Julia. sd se Teodoro Walter Sandra 15 25 19 17 24 15 15 18 10 0 15 17 w w .k la A B C D Julia 16 19 15 19 w Z =19 + 15 + 24 + 19 = 77 9. Cuatro expendedores de gasolina A, B, C, D requieren 50.000; 40.000; 60.000; 40.000 galones de gasolina respectivamente. Es posible satisfacer estas demandas a partir de las localidades 1,2,3 que disponen de 80.000; 100.000; 50.000 galones respectivamente. Los costos de despachar 1000 galones de gasolina son La matriz de costos es: A B 1 2 3 DEMANDA 50 C D OFERTA 70 60 60 60 50 80 60 70 80 50 80 60 40 60 40 80 100 50 230 Minimizar Z= (70X11+60X12+ 60X13 + 60X14) + (50X21+80X22+ 60X23 + 70X24) + (80X31+50X32+ 80X33 + 60X34) www.klasesdematematicasymas.com Preparado por: Oscar Restrepo Sujeto a Oferta X11+X12+ X13 + X14≤ 80 X21+X22+ X23 + X24≤ 100 X31+X32+ X33 + X34≤ 50 Demanda X11+X21+ X31 ≥ 50 X12+X22+ X32 ≥ 40 X13+X23+ X33 ≥ 60 X14+X24+ X34 ≥ 40 Con Xij≥0, para i=1,2,3 j=1,2,3,4 em at ic a sy m as .c om Para solucionarlo se utiliza WINQSB y se encuentra que: em at Es decir, X11= 50, X12= 0, X13= 0, X14 =0, X21=0, X22=40, X23=10, X24= 40 X31=0, X32= 0, X33=0, X34=0 Z = 14100 w w w .k la se sd 10. Una fábrica produce dos modelos de un producto, cada modelo se ensambla con dos tipos de piezas A y B. El modelo 1 requiere 20 piezas de A y 45 de B; el producto 2 requiere 25 piezas de A y 70 piezas de B; la fábrica recibe de sus proveedores 1675 piezas de A y 4250 de piezas de B a la semana. Las unidades a producir en la semana si el precio de venta de A es de 10000 y de B 15000 si su costo de producción es de A=4500 y de B= 12000. Cuántas unidades debe fabricar de cada uno para maximizar sus beneficios y cuál sería su problema Dual. X1 es el número de modelo 1 X2 es el número de modelo 2 Función Objetivo: Maximizar utilidades Z = (10000 – 4500)X1 + (15000 – 5000)X2 Z = 5500X1 + 5000X2 Sujeto a 20X1 + 25X2 ≤ 1675 45X1 + 70X2 ≤ 4250 X1, X2 ≥0 Restricción piezas de A Restricción piezas de B Modelo estándar www.klasesdematematicasymas.com Preparado por: Oscar Restrepo Z – 5500X1 – 5000X2 + 0S1 + 0S2 + 0S3 = 0 20X1 + 25X2 + S1 = 1675 45X1 + 70X2 + S2 = 4250 Z S1 S2 Z 1 0 0 X1 -5500 20 45 X2 -5000 25 70 S1 0 1 0 S2 0 0 1 bi 0 1675 4250 Z X1 S2 Z 1 0 0 X1 0 1 0 X2 1875 5/4 55/4 S1 275 1/20 -9/4 S2 0 0 1 bi 460625 335/4 1925/4 w w w .k la se sd em at em at ic a sy m as .c om El tablero es óptimo. X1 = 335/4, X2= 0, S1 = 0, S2 = 1925/4, Z = 460625 www.klasesdematematicasymas.com