Ejemplos de planteamientos de Programación Lineal
Anuncio

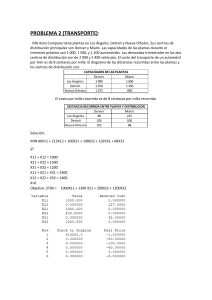
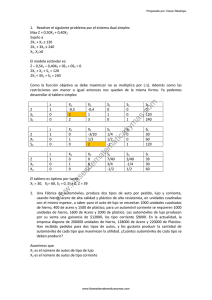
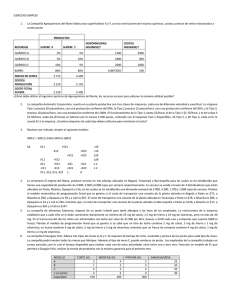
Investigación de Operaciones Ejemplos de planteamientos de Programación Lineal 1. Una familia campesina es propietaria de 125 acres y tiene fondos para $40 000 para invertir. Sus miembros pueden producir un total de 3 500 horashombre de mano de obra durante los meses de invierno y 4 000 horashombre durante el verano. En caso de que no se necesite una parte de estas horas-hombre, los jóvenes de la familia las emplearán para trabajar en un campo vecino por $5 la hora durante los meses de invierno y por $6 la hora en el verano. Pueden obtener el ingreso en efectivo a partir de tres tipos de cosecha: soya, maíz y avena y dos tipos de animales de granja: vacas lecheras y gallinas ponedoras. Para las cosechas no se necesita inversión, pero cada vaca requerirá un desembolso de $1 200 y cada gallina costará $9. Cada vaca necesita 1.5 acres, 100 horas-hombre durante el invierno y otras 50 horas-hombre durante el verano; cada una producirá un ingreso anual neto de $1 000 para la familia. Las cifras correspondientes para cada gallina son: nada de terreno, 0.6 horas-hombre durante el invierno, 0.3 horashombre en el verano y un ingreso anual neto de $5. Caben 300 gallinas en el gallinero y el corral limita el ganado a un máximo de 32 vacas. Las estimaciones de las horas-hombre y el ingreso por acre plantado con cada tipo de cosecha se indican en la tabla. La familia quiere determinar cuántos acres debe sembrar con cada tipo de cosecha y cuántas vacas y gallinas debe mantener para maximizar su ingreso neto. Formule el modelo de PL para este problema. Horas-hombre en invierno Horas-hombre en verano Ingreso neto anual ($)/acre Soya 20 50 600 Maíz 35 75 900 Avena 10 40 450 Tomado de “Introducción a la Investigación de Operaciones” Hillier/Lieberman Quinta Edición, Mc Graw Hill Cap. 3, Problemas del final del capítulo. ____________________________________________________________________________________ Diana Cobos 18 Investigación de Operaciones Sol. Problema 2 Sean = acres destinados a soya = acres destinados a maíz = acres destinados a avena = número de vacas = número de gallinas = exceso de horas-hombre en el invierno = exceso de horas-hombre en verano Luego entonces la función objetivo puede expresarse como: Sujeta a: acres inversión h-h invierno h-h verano vacas gallinas ____________________________________________________________________________________ Diana Cobos 19 Investigación de Operaciones Ejemplos de planteamientos de Programación Lineal 2. Cierta compañía tiene tres plantas con un exceso en su capacidad de producción. Las tres pueden fabricar un determinado producto y la gerencia ha decidido usar parte de la capacidad adicional para esto. El producto puede hacerse en tres tamaños: grande, mediano y chico, que darán una ganancia neta de $420, $360 y $300, respectivamente. Las plantas tienen capacidad de mano de obra y equipo para producir 750, 900 y 450 unidades diarias cada una, sin importar el tamaño o la combinación de tamaños de que se trate. La cantidad de espacio disponible para almacenar material en proceso impone también una limitación en las tasas de producción del nuevo producto. Se cuenta con 13 000, 12 000 y 5 000 ft 2 de espacio en las plantas 1, 2 y 3, para los materiales en proceso de la producción diaria de este producto. Cada unidad grande, mediana y chica que se produce requiere 20, 15 y 12 ft2 respectivamente. Los pronósticos de mercado indican que se puede vender 900, 1 200 y 750 unidades diarias, correspondientes a los tamaños grande, mediano y chico. Con el fin de mantener una carga uniforme de trabajo entre las plantas y para conservar alguna flexibilidad, la gerencia ha decidido que la producción adicional que se les asigne emplee el mismo porcentaje de la capacidad adicional con que cuentan. El gerente quiere saber cuántas unidades de cada tamaño debe producir en cada planta para maximizar la ganancia. Formule el modelo de PL para este problema. ____________________________________________________________________________________ Diana Cobos 20 Investigación de Operaciones Solución Plantas 1 2 3 Capacidad unid/día 700 900 450 Espacio ft2 13,000 12,000 5,000 Producto Grande Mediano Chico 420 360 300 Ganancia 900 1 200 750 Demanda Sean = unidades de tamaño i producidas por la planta j i = 1, 2, 3; j = 1, 2, 3 La función objetivo es Max X0 = 420 (X31 + X32 + X33) + 360 (X21+ X22 + X23) + 300 (X11 + X12 + X13) Restricciones de mercado son: Grande Mediano Chico X31 + X32 + X33 X21 + X22 + X23 X11 + X12 + X13 900 1 200 750 Capacidad de producción Planta 1 Planta Planta X31 + X21 + X11 2X32 + X22 + X12 3X33 + X23 + X13 750 900 450 Espacio Planta 1 Planta 2 Planta 3 20 X31 + 15 X21 + 12 X11 20 X32 + 15 X22 + 12 X12 20 X33 + 15 X23 + 12 X13 13 000 12 000 5 000 ____________________________________________________________________________________ Diana Cobos 21 Investigación de Operaciones La producción asignada a cada planta debe ser proporcional a su capacidad Luego entonces el problema ya simplificado es: Max X0 = 420 X31 + 420 X32 + 420 X33 + 360 X21 + 360 X22 + 360 X23 + 300 X11 + 300 X12 + 300 X13 Sujeta a: Grande Mediano Chico X31 + X32 + X33 X21 + X22 + X23 X11 + X12 + X13 900 1 200 750 Restricciones de mercado Planta 1 Planta 2 Planta 3 X31 + X21 + X11 X32 + X22 + X12 X33 + X23 + X13 750 900 450 Capacidad productiva Planta 1 Planta 2 Planta 3 20 X31 + 15 X21 + 12 X11 20 X32 + 15 X22 + 12 X12 20 X33 + 15 X23 + 12 X13 13 000 12 000 5 000 Espacio 750 X32 + 750 X22 + 750X12 - 900 X31 - 900 X21 - 900 X11 = 0 900 X33 + 900 X23 + 900 X13 - 450 X32 - 450 X22 - 450X12 = 0 i = 1, 2, 3 Proporcionalidad en la capacidad j = 1, 2, 3 ____________________________________________________________________________________ Diana Cobos 22 Investigación de Operaciones Ejemplos de planteamientos de Programación Lineal 3. Un inversionista tiene oportunidad de invertir al principio de cada uno de los próximos 5 años en 4 tipos diferentes de instrumentos de inversión: A, B, C y D. Cada dólar invertido en A al principio de cualquier año, retribuye $ 1.40 (una ganancia de $0.40) 2 años después (a tiempo para la reinversión inmediata). Cada dólar invertido en B al principio de cualquier año retribuye $1.70, 3 años después. Las inversiones C y D estarán disponibles para inversión una sola vez en el futuro. Cada dólar invertido en C al principio del año 2 da $1.90 al final del año 5. Cada dólar invertido en D al principio del año 5 retribuye $1.30 al final de ese año. El inversionista tiene $60 000 para iniciar y desea saber cuál plan de inversión maximiza la cantidad de dinero acumulada al principio del año 6. Formule el modelo de programación lineal para este problema. Tomado de: Introducción a la Investigación de Operaciones Frederick S. Hillier / Gerald J. Lieberman Quinta Edición Mc Graw Hill ____________________________________________________________________________________ Diana Cobos 23 Investigación de Operaciones Sol. Problema 3 Solución al ejemplo del inversionista A B C D 1 -1 -1 2 -1 -1 3 -1 +0.4 -1 4 -1 +0.4 5 6 +0.4 +0.4 +0.7 +0.7 +0.7 +0.9 +0.3 -1 -1 Sean: Ai = cantidad invertida en A en el año i (i =1, 2, 3, 4) Bi = cantidad invertida en B en el año i (i =1, 2, 3) C2 = cantidad invertida en C en el año 2. D5 = cantidad invertida en D en el año 5. Ri = cantidad no invertida en el año i (i = 1, 2, 3,4) Entonces el problema queda expresado como: Max X0 = 1.9C2 + 1.7B3 +1.4A4 +1.3D5 Sujeta a: A1+ B1+ R1 = 60 000 A2+ B2+ C2+ R2 = R1 A3 +B3+ R3 = 1.4A1+ R2 A4+ R4 = 1.4A2+1.7B1+ R3 D5 = 1.4A3+1.7B2+ R4 A1, A2, A3, A4, B1, B2, B3, C2, D5, R1, R2, R3, R4 0 ____________________________________________________________________________________ Diana Cobos 24