σ ω σ σ ω ω σ ω
Anuncio

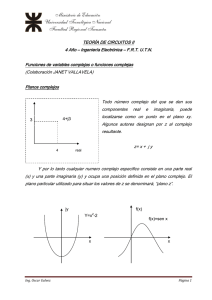
UNIVERSIDAD NACIONAL ABIERTA Y A DISTANCIA – UNAD ESCUELA DE CIENCIAS BÁSICAS, TECNOLOGÍA E INGENIERÍA 243005 – SISTEMAS DINÁMICOS POLOS Y CEROS Hay que recordar que un número complejo está compuesto de una parte real y una parte imaginaria, ambas son constantes. Si la parte real y/o la parte imaginaria son variables, el número complejo se denomina variable compleja. La transformada de Laplace usa la notación s para la variable compleja, esto es: s j (1) Donde es la parte real y es la parte imaginaria. De forma gráfica en el plano s , la componente real está representada por el eje en la dirección horizontal y la componente imaginaria se mide a lo largo del eje vertical j . La figura 1 muestra el plano complejo s , en donde cualquier punto arbitrario s s1 está definido por las coordenadas 1 y 1 , o simplemente s1 1 j1 . j 1 s1 1 j1 1 0 Figura 1 Plano complejo s Se dice que la función G(s) es una función compleja, si para cada valor de s existen uno o más valores correspondientes de G(s) . Debido a que s se define con partes real e imaginaria, la función G(s) también está representada por sus partes real e imaginaria, esto es: G ( s ) Gx jG y (2) En donde Gx y G y son cantidades reales. La magnitud de G(s) es: G ( s ) Gx2 G y2 (3) Y el ángulo de G(s) es: Gy (4) Gx tan 1 Página 1 de 4 UNIVERSIDAD NACIONAL ABIERTA Y A DISTANCIA – UNAD ESCUELA DE CIENCIAS BÁSICAS, TECNOLOGÍA E INGENIERÍA 243005 – SISTEMAS DINÁMICOS El ángulo se mide en sentido opuesto al movimiento de las manecillas del reloj, a partir del eje real positivo. El complejo conjugado de G(s) es: G ( s) Gx jGy (5) Si para cada valor de s existe sólo un valor correspondiente de G(s) , se dice que G(s) es una función univaluada. Por lo general, las funciones complejas que se encuentran en el análisis de sistemas de control lineales son funciones univaluadas de s . Una función G(s) se llama función analítica en una región del plano s , si la función y todas sus derivadas existen en dicha región. Ejemplo 1 Determine si la siguiente función es analítica: G( s) 1 s( s 1) Solución: Es analítica en cada punto del plano s , excepto en los puntos s 0 y s 1 , ya que en estos dos puntos el valor de la función tiende a infinito. Ejemplo 2 Determine si la siguiente función es analítica: G( s) s 2 Solución: La función es analítica en todos los puntos del plano s . Los puntos en el plano s en los cuales la función G(s) es analítica se denominan puntos ordinarios, en tanto que los puntos en el plano s en los cuales la función G(s) no es analítica se denominan puntos singulares. Los puntos singulares en los cuales la función G(s) o sus derivadas tienden a infinito se denominan polos. Página 2 de 4 UNIVERSIDAD NACIONAL ABIERTA Y A DISTANCIA – UNAD ESCUELA DE CIENCIAS BÁSICAS, TECNOLOGÍA E INGENIERÍA 243005 – SISTEMAS DINÁMICOS Ejemplo 3 Encuentre los polos de la siguiente función: G( s) 1 s 1 Solución: La función tiene un polo en s 1 . Los puntos en los cuales la función G(s) es igual a cero se denominan ceros. Ejemplo 4 Encuentre los polos y los ceros de la siguiente función: G( s) 10(s 2) s( s 1)( s 3)2 Solución: La función tiene polos sencillos en s 0 y s 1 , tiene un polo repetido o de orden 2 en s 3 , además tiene un cero sencillo o simple en s 2 . REFERENCIAS BIBLIOGRÁFICAS A continuación se presenta el listado de las referencias bibliográficas requeridas: Dorf, R & Bishop, R. (2011). Mathematical models of systems. En: Modern control systems. (12a. ed.). (pp. 49-160). Estados Unidos: Prentice Hall. Golnaraghi, F. & Kuo, B. (2010). Mathematical foundation. En: Automatic control systems (9a.ed.). (pp. 16-103). Estados Unidos: John Wiley & Sons. Ogata, K. (2010). Modelado matemático de sistemas de control. En: Ingeniería de control moderna (5a. ed.). (pp. 13-62). Madrid, España: Pearson Education. Nise, N. (2011). Modeling in the frequency domain. En: Control Systems Engineering (6a ed.). (pp. 33-116). Estados Unidos: John Wiley & Sons. A continuación se presenta el listado de las referencias bibliográficas complementarias: Curso virtual de análisis de sistemas dinámicos. Recuperado en http://www.virtual.unal.edu.co/cursos/ingenieria/2001619/index.html Determinar la función de transferencia dados los ceros y polos. Recuperado en https://www.youtube.com/watch?v=8BMetYZGbdQ Determinar los ceros y polos de la función de transferencia. Recuperado en https://www.youtube.com/watch?v=LFBsmjbpMAM Design and analyze control systems. Recuperado en http://www.mathworks.com/help/control/index.html Expresiones alternativas de la función de transferencia. Recuperado en https://www.youtube.com/watch?v=5-mB9eDUKDU Página 3 de 4 UNIVERSIDAD NACIONAL ABIERTA Y A DISTANCIA – UNAD ESCUELA DE CIENCIAS BÁSICAS, TECNOLOGÍA E INGENIERÍA 243005 – SISTEMAS DINÁMICOS Teoría de control básica. Recuperado en http://controltheory.org/index_spa.html Página 4 de 4