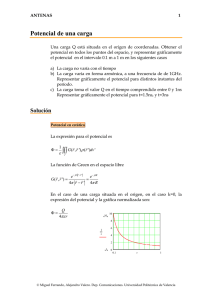
nˆ E ε σ = о E ε=σ - U
Anuncio

Conductores E = 0 dentro del conductor (Franklin, Priestley) V = Const. (equipotencial) r σ E= n̂ ε0 σ = ε0E n Energía electrostática de N conductores: 1 N W = ∑ Q i Vi 2 i =1 Condensadores Símbolo: Dos conductores, con cargas Q y –Q Diferencia de potencial = V Coulomb [C] = [Faradio] = V Q = CV ∴ Q C= V Encontrar la capacidad de un condensador plano. Distancia = d A r σn̂ E= = C te. ε0 ∴ Q σA C= = V Ed d V = Ed ∴ ε0A C= d Area = A Q = σA Encontrar la capacidad de un condensador esférico r E= Q r̂ 2 4πε 0 r R2 −Q V2 − V1 = 4πε 0 ∫ dr +Q = 4πε 0 r2 1 1 Q (R2 − R1 ) − = R1 R2 4πε 0 R2 R1 R1 R 1R 2 Q C= = 4πε 0 (R 2 − R 1 ) V2 − V1 Si R 2 → ∞, C → 4πε 0 R 1 Encontrar la capacidad de un condensador cilíndrico R2 R2 V1 − V2 = ∫ E r dr = ∫ R1 Qdr 2πε 0 Lr R1 R2 V1 − V2 = L R1 R2 Q 2πε 0 L ∫ dr r R1 R2 Q V1 − V2 = ln 2πε 0 L R 1 C= Q 2πε 0 L = V1 − V2 R ln 2 R1 Energía acumulada en un condensador 1 N W = ∑ Q i Vi 2 i =1 N=2 Q1 = Q para N conductore s 1 W = (Q 1 V1 + Q 2 V2 ) 2 Q 2 = −Q 1 W = Q (V1 − V2 ) 2 1 W = (QV1 − QV2 ) 2 1 Q 2 CV 2 W = QV = = 2 2C 2 Asociación de condensadores: En serie y en paralelo. En serie: Q1 = Q2 = Q Q = C1V1 = C 2 V2 V1 = Q Q V1 + V2 = V = + C1 C 2 1 1 1 = + C C1 C 2 C= Q C1 V2 = ∴ C1C 2 C1 + C 2 Q C2 1 1 V = Q + C1 C 2 En paralelo: V1 = V2 = V Q1 + Q 2 = Q = (C1 + C 2 )V ∴ C = C1 + C 2 Un condensador de placas planas, cargado con Q: Se alejan las placas: d1 → d2 Q = Const. Q2 W2 = 2C 2 Q2 W1 = 2C1 C1 = d2 > d1 ε0A d1 W2 d 2 = W1 d1 C2 = > 1 ε0A d2 Q 2 d1 W1 = 2ε 0 A Q2d 2 W2 = 2ε 0 A Q 2 (d 2 − d1 ) W2 − W1 = >0 2ε 0 A