Estimación robusta - Instituto Nacional de Estadistica.
Anuncio

ESTADISTICA ESPAÑOLA
Vol. 36, Núrn. 137, 1994, págs. 327 a 387
Estimación robusta
por
RUBEN H. ZAMAR
University of British Columbia
RESUMEN
En este artícula se presentan algunos enfoques recientes de la
teoría de estimación robusta, particularmente resultados en el área
de minimización del sesgo máximo. Se describen algunos estimadores robustos de regresión y se introduce la definición de curva de
sesgo máximo. Se discute !a relación entre esta curva y la sensitividad a errores groseros. Estos conceptos se ilustran en el caso de
modelos sencillos de posición y dispersión.
Palabras clave: estimadores minimax, sesgo máximo, sensibilidad a
contaminacíones.
C/asificación AMS: 62Jxx, 62H12.
1.
INTRODUCCION
Una práctica muy común en estadística (tanto teórica como aplicada) es suponer que los datos han sido generados por un mecanismo aleatorio y que éste
puede ser representado por un miembro F^ de la familia paramétrica de funciones de distribución
^={F^:HE O}
[1]
E^.^EAE^I^TI(^^1 E^^Ei,1tic)I„^
La característica más sobresaliente de estos modelos matemáticos es la suposición de que el mecanismo aleatorio que generó las observaciones es totalmente conocido a excepción del parámetro desconocido e. Naturalmente, el
principal problema en estos casos es la estimación de e usando un estimador 6„
con buenas propiedades estadisticas: sesgo pequeño o nulo y varianza pequeña. Un método que, en general, satisface estos requerimientos es el método de
máxima verosirnilitud. Muchos de los métodos de estimación usados en la práctica fueron derivados a partir de modelos paramétricos, notablemente modelos
normales o gaussianos. Además, las prapiedades estadísticas de estos métodos han sido estudiadas a la luz de tales modelos.
Desafortunadamente, ios mecanismos aleatorios que producen los datos en
la práctica muy raramente obedecen con exactitud a un modelo paramétrico. En
muchos casos, sin embargo, el modelo paramétrico provee una razonable aproximación del mecanismo estocástico F que cantrola la generación de las observaciones.
En resumen, la utilización del modelo [1 ] y, consecuentemente, el empleo de
^
estimadores de máxima verosimilitud 8„ se justifica usualmente por los siguientes argumentos:
a)
EI modelo [1 ] se cumple aproximadamente.
b)
Las buenas propiedades del método utilizado para estimar 9{máxima
verosimilitud) son continuas, de manera que, si el modelo es aproxima^
damente válido, entonces en es aproximadamente óptimo.
Mientras que la propiedad (a ) es cierta con frecuencia, la propiedad {b } no
lo es en muchos casos que incluyen el importante modelo normal. En efecto,
puede demostrarse que la eficiencia de la media aritmética X{el estimador óptimo bajo el modelo de pasición normal} puede ser arbitrariamente próxima a
cero para distribuciones que son arbitrariamente próximas a la normaf. Si, por
ejemplo, tenemos veinte mediciones independientes X; = µ+ E; , diecinueve de
las cuales son normales con desviación típica . 03 y una es un outlier x, y si el
promedio de las diecinueve observaciones normales es 1.0, entonces X=.95 +
+.05x ^^, si x-^ ^. Si, por ejempfo, x= 2.8, entonces X= 1.09, a pesar de
que, en este caso, las diecinueve observaciones normales estarán típicamente
contenidas en el intervalo (0.91, 1.09). Además, las densidades normales N(^, 6)
y .95N (1, 6} + .05N ( 2.8, 6) (a = . 03) son prácticamente indistinguibles,
EI ejemplo del párrafo anterior muestra que el estimador de máxima verosimilitud bajo el modelo normal ( en este caso, la media muestral) puede producir
estimaciones muy ineficientes si los datos son producidos por una distribución
que es próxima, pero no exactamente igual, a la normal. La conclusión, en mi
opinión, es que el hecho de que el modelo normal es solamente una buena
E•:ti^^fl?^^tAC'ION itOBt'S'fA
^?y
aproximación del mecanismo aleatorio que generó las observaciones es algo
que debe tenerse en cuenta explícitamente en el momento de escoger el estimador µn de µ.
Una manera de incorporar explícitamente ia cuestión de la naturaleza aproximada del modelo paramétrico F,^ es suponer que la distribución F pertenece a la
familia ^^ definida como
.^E _ { (1 -- E) F^ + ^H : 8 E O}
[2)
donde o<^< 0.5 es fijo y H es arbitraria y desconocida. Esta familia de contaminación
inicialmente propuesta por Tukey
es rnuy simple y, además, re#leja fielmente situaciones en que la mayoría de !as observaciones provienen de!
modelo [1 ], pero una pequeña fracción ^ de las observaciones son outlíers generados po r H.
Por supuesto, hay otros tipos de entornos de F® que podrían usarse en lugar
de [2]. Por ejemplo, entornos basados en distancias entre dístríbuciones como
la distancia de variación total o la distancia de Levy. Sin embargo, el entorno de
contaminación [2] tiene la doble ventaja de ser simple y apropiado.
EI comportamiento de un estimador consistente 6„ de e, bajo el modelo paramétrico^ Fe , puede medirse de forma natural en términos de la varianza asintótica A V (e„ , Fg ). Por otro lado, cuand© uno supone que la distribución F es un ele^
mento de ^^, los estimadores 6„ serán en generai asintóticamente sesgados y,
por lo tanto, el sesgo asintótico es un aspecto importante a considerar. Otro aspecto importante es el hecho de que la distribución F no está completamente
especificada, puesto que H es desconacida.
En lo que sigue supondremos que el es#imador 8„ depende de los datos únicamente a través de la distribución ernpí rica
Fn (z) =n 1 ^ bz,(z)
donde ^ Z (z )= 1 si cada elemento del vector z es menor o igual que el correspondíenté elemento del vector ^; , y b Z( z )= 0 en otro caso. Por lo tanto, 8n
,
puede escribirse corno
^^O
E^_^^1^^^[^)I^^T^^I(':1^ f^S1'A:^i^E.,1
n
También supondremos que el funcional H(F^ ) admite una extensión natural
^
H(F), con F en un conjunto de distribuciones que contiene a la familia F. Finalmente, supondrernos que el funcional 8 (F) es Fisher consistente:
n
6(Fe)=8, b'6E O
A
y que e^ ( F^ ) es consistente:
^
^
lim ^ (F^ } _ 9 {F), a.s. ^F]
^
para toda F E F. . Como, en general, H( F)^ 6 cuando F^^F , deberemos pres^
tar especial atención a la cuestián del sesgo asintótico de 8{F„ ).
A menudo, el espacio paramétrico O tiene ciertas propiedades de invarianza
(o equivarianza} que deben ser respetadas por la medida que se proponga para
evaluar el sesgo asintótico. Por ejemplo, en el caso del modelo simple de posición y dispersión [^ _(µ, 6}J, las medidas del sesgo asintótico del estimador
µ{F„ ) de µ y del estimadar á(F„ ) de 6 deben ser invariantes ante cambios de
posición y escala. Por ejemplo, las medidas de sesgo
lµ (F)-µl
6
Y
^s (F)
^
6
-1^
poseen las propiedades de invarianza deseadas. En general, el sesgo asintótico
del estimador 8(F) cuando F varia sobre .^t; , puede definirse coma
^
b^{F,e}=d[9((1 -^) F^+^H), 9]
donde d es una distancia que respeta las invariancias naturales del espacio O.
En este artículo únicamente consideraremos estimadores que tienen las propiedades de equivarianza requeridas por la naturaleza del espacio paramétrico.
Por ejemplo, sólo trabajamos con estimadores de posición que son equivariantes ante cambios de posición y escala y con estimadores de dispersión que son
invariantes con respecto a cambios de posición y equivariantes con respecto a
cambios de escala. En vista de las propiedades de invarianza de la distancia d y
de las propiedades de equivarianza de ios estimadores considerados en este ar-
F:^f1^1,^^c'!c)ti Kc)Bl':^ 1 :^
^^I
tículo, podemos concentrar nuestra atención en un valor canónico Ho de H,
como, por ejemplo, H^ _(0, 1) en el caso de rnodelos de posición y dispersión.
Más precisamente:
^
bé (F, 8) = d^ 8((1 -- E) FA + cH), 8]
^
= d[ 6((1 -- E} Feo + EH ), 80]
Por ejemplo, en ef caso de modelos de posición y dispersión, los sesgos del
estimador µ( F) de posición y 6( F) de dispersión se reducen a
lµ (F)-µl
^
=^µ(F)I
a
Y
^
6 (F)
^
,^
--1 (=^a(F)-1 ^
E6]
respectivamente.
Este trabajo está organizado como sigue. En la sección 2 discutiré los dos
principales aspectos de la teoría de robustez: eficiencia y estabilidad. En esta
sección también mencionaré brevemente los diferentes enfoques utilizados para
medir la estabilidad de un estimador. En las secciones 3 y 4 describiré dos irnportantes familias de estimadores robustos de regresión. En la sección 5 ilustraré el cálculo de la función de sesgo máximo y la derivación de estimadores de
sesgo minimax en el casa del modelo simple de posición. En la sección 6 daré
algunas conclusiones.
2. DEFINICIONES DE ROBUSTEZ
Ahora pasaremos a consíderar diferentes formas en que se puede medir ia
^
robustez del estimador 8 de 6.
Habiando en términos generales y desde un punto de vista ampiio e infor^
mal, se puede decir que el estimador {o funcianal) 8 (Fn ) es robusto si su cornportamiento es relativamente bueno y estable cuando F varía sobre el entorno
^
^f del modelo paramétrico F^. En otras palabras, el estimador 6(F^ ) debe poseer las siguientes dos propiedades:
EF1ClENCIA: 6 (Fn ) se comporta bien cuando el modelo paramétrico central
F = F^ se satisface.
F^!i l A[)15.^ 1('r1 E-.^PA!^i()I^A
n
ESTAB/LIDAD: EI buen comportamiento de 6{F^ ) se preserva cuando F varia sobre _`^._ .
^
Para cumplir el requerimiento de eficiencia,
8{F„ ) debe ser comparabie con
^
el estimador de máxima verosimilitud ^(F^ ) cuando F= Fe. Más precisamente:
^
1. 9(F} debe ser consistente en el sentido de Fisher
^
e(F^}=8,de
^
6{
F) debe ser asintóticamente normal, con matriz de covarianzas C^( F) y
2.
traza { C ^( FH }} ^ 1+ b
traza { C ,^ ( F^ ) }
[7]
donde ^> 0 es un número pequeño (b = 0.05 y^= 0.10 son valores usuales
de s).
Notemos que la eficiencia asintótica de un estimador multivariante se puede
medir de manera natural en términos de la traza de su matriz de covarianzas
asintótica, esta es, de su «varianza asintótica generalizada». La formalización
del requerimiento de estabilidad ha dada lugar a varios en#oques en la teoría de
robustez: Robustez Cualitativa, Robustez Cuantitativa y Robustez Infinitesimal.
Gada uno de estos enfoques será brevemente discutido a continuación.
Robustez Cualitativa
^
Este enfoque, iniciado par Hampel (1971), considera que el funcionai 9(F}
^
es estable {cualitativamente robusto) si 8 es continuo en una cierta manera {los
detalles técnicos pueden encontrarse en la referencia). Robustez cualitativa es
una propiedad muy básica y, por lo tanto, estimadores que no poseen esta propiedad pueden ser descartados desde el punto de vista de la robustez. Por otro
lado, esta teoría no es completamente satisfactoria por cuanto no permite comparaciones dentro de la clase de estimadores que son cualitativamente robustos.
Robustez Cuantivativa
Este enfoque, originado por Huber ( 1964), intenta cuantificar la estabilidad
^
de 9(F). Esto puede ser hecho en términos del sesgo asintótico máximo:
B ^ (E)=supbe{F,9)
FE 'tt.
E:S"T1!vfAClON RC)Bl!S"1^.A
o en términos de la varianza asintótica generalizada máxima:
AVé (^} = sup traza (C^ (F))
F E .`j F
EI punto de ruptura:
E*=sup{^:Be(
^
representa la mayor fracción de contaminación que el estimador e puede tolera^r
antes de camenzar a comportarse en forma totalmente aberrante. Para que ^
pueda ser considerado estable
cuantitativamente robusto
de acuerdo con
esta teorí a, el sesgo máximo B' ^(^) y la varianza máxima AV ^ (^) deben ser relativamente pequeños. ^bsérvese que el requerimiento de que B^ (^) sea pequeño er^uivale a que la primera condición de eficiencia la consistencia en el senn
sea relativarnente preservada cuando Fvatido de Fisher de 9 (b,^ (Fe , 8) = 0)
ría sobre ^^. Similarmente, el requerimiento de que AV ^(^) sea pequeña es
equivalente a que la segunda condición de eficiencia sea relativamente preservada cuando F varía sobre ^E.
Huber ( 1964) encantró los estimadores que minimizan B ^(E) y AV ^(^) en la
ciase de estimadores M de posición y abrió el camino para el desarrollo de la
teoría de robustez cuantitativa. Como estos estimadores minimizan el sesgo
máximo y la varianza máxima, son Ilamados estimadores minimax.
^
En general, la desviación típica de un estimador 6^ es típicamente de orden
/^, mientras que su sesgo asintótico, si existe, es de orden uno. Entances,
el sesgo asintótico máximo será el término dominante del error cuadrático medio
máximo cuando se permite sesgo asintótico bajo ^E. Es precisamente por esta
razón que Huber ( 1964), para poder derivar su famoso resultado sobre varianza
minimax, evitó ia posibilidad de sesgo asintótico restringiendo la familia }^^ al
subconjunto de funciones simétricas.
Finalmente, como todos los estimadores que consideraremos en este trabajo
son equivariantes, no hay pérdida de generalidad en suponer que 80 = 0. Entonces, el argumento «8» será, de ahora en adelante, omitido en b y B. La distribución bajo el modelo paramétrico central será denotada Fo.
Robustez Infinitesimal
Una manera muy útil de simplificar el estudio del sesgo máximo es aproximar linealmente B^ (^) cerca de cero:
B ^ (^) = B' ^ (0} ^ + o (^)
y concentrar la atención en la cantidad B' é(
F.S"T^,^1C)15^1^1C'A F-:tiE'ANOL^1
Sea bz la función de distribucián que asigna masa uno al punto z. La función
^
^
de infJuencia, IF (^ , z), y la sensibilidad a errores groseros, y(e), fueron definidas por Hampe! t 1974} como
^
lF {8 , z ) = lim
F --^o
^
^
8((1 --E) Fo+E^=)-6(Fo)
^
Y
^
^
y(e) = suP II ^F(e, z) II
z
respectivamente, suponiendo que ei límite existe.
A pesar de ciertas diferencias formales descritas a continuación, cuando y{8}
es finita (caso regular^ se cumple que
^
r (e) = B' ^ (o)
^
^as diferencias formales entre y(6) y B'^ (0) radican en: a) el orden en el que
se aplican la derivada y el supremo, y b) los conjuntos considerados para calcular el supremo. En e! caso de B',^ (o) el supremo se aplica primero y la diferenciacián después, mientras que en el caso de y(9} Ca diferenciación se apCica primero y el supremo después. Con respecto a b), en el caso de B',^ {o) el supre^
mo se aplica sobre el entorno completo ^^, en el caso de y(9) el supremo es
aplicada sobre el sub-entorno incluyendo distribuciones de masa puntual únicamente.
Durante muchos años, las propiedades de «tener influencia limitada» (y (8)
finita) y de «ser robusto» fueron consideradas como propiedades equivalentes.
Sin embargo, la influencia limitada no es una condición necesaria ni suficiente
de robustez: existen estimadores robustos con influencia ilimitada y estimadores
no robustos con influencia limitada. Los estimadores MM y Tau de regresión
descritos en la sección 3 son ejemplos de los primeros. A pesar de tener función
de influencia no acotada, estos estimadores son eficientes bajo el modelo normal y estables cuando este modelo no se cumple. EI alto punto de ruptura y la
eficiencia de estos estimadores es independiente del número de variables independientes y de su distribución. Un ejemplo triviaC de estimadores no robustos
con influencia acotada lo ofrecen los estimadores M de posición que usan la
desviación típica como estimador auxiliar de dispersión. Un ejemplo más interesante lo ofrecen los est'rmadores M generalizados de regresión (GM) descritos
en la sección 4, cuando el númera de variables independientes es grande. Los
Es^r^irwAC^c^^N Kc^^^!s^r.A
335
estimadores GM tienen influencia acotada, pero Maronna, Bustos y Yohai
(1979) mostraron que el punto de ruptura de estos estimadores es menor o igual
que 1/^p , donde p es el número de variables independientes.
3.
ESTIMADORES QUE MINIMIZAN UNA FUNCION DE LOS RESIDUOS
Una buena parte de la teoría de robustez se ocupa del problema de estimación robusta en el modelo de regresión lineal. Existen muchas propuestas de estimadores robustos de regresión y en esta sección nos ocuparemos sólo de algunas de ellas: estimadores S, ^ y MM, definidos por Rousseeuw y Yohai (1984),
Yohai y Zamar (1988) y Yohai (1987}, respectivamente. Estos estimadores tienen la propiedad de minimizar una función objetivo que depende de los datos
únicamente a través de los residuos. En la próxima sección nos ocuparemos de
otra clase de estimadores de regresión Ilamados estimadores M generalizados.
Estos estimadores minimizan una función objetivo más compleja que depende
de los datos a través de Ios residuos y de las variables independientes.
Los estimadores S no pueden ser estables y eficientes al mismo tiempo,
pero tienen la importante ventaja de poder calcularse directamente a partir de
los datos sin necesidad de estimadores iniciales de regresión ni dispersión. Por
esta razón, los estimadores S son a menudo utilizados como estimadores iniciales en los algoritmos de cálculo de estimadores robustos.
Los estimadores ^ y MM pueden cornbinar las propiedades de estabilidad y
eficiencia y se calculan a partir de estimadores S.
Para poder definir los estimadores S de regresión se definirán primero los
estimadores M de escala y dispersión.
Estimadores M de Escala
Huber (1964) definió los estimadores M de la escala de las observaciones
..., r^ como la solución de la ecuación
=b
La función x normalmente satisface las siguientes condiciones: i) x(y )= x(-y );
ii) x es no-decreciente en [0, ^}; iii) x es continua excepto en un número finito de
puntos, y iv} x(^) = 1. Por otro lado, la constante b se toma normalmente igual a
,
Fo x( Y), donde Fo es una distribucion especificada ( e.g. Fo (y) = 1- e-y }.
F^S^I^A[.)IS^^I.ICA ESF',=^Iti(}LA
Martin y Zamar {1989} mostrar-on que, cuando las observaciones r; son positivas,
Mediana {r; } I Fó ' (0.5)
es aproximadamente minimax entre ios estimadores M de escala. Observamos
que la mediana carresponde al caso en que la función ^ es del tipo 0-1 :
x(r )= 0,
= 1,
cuando y<_ a
[9]
cuando y > a
con a= F^ '(0.5). En efecto, cuando n es par y la función x es definida por [9J,
b=EFox(Y}=PF^{Y>F^' (.5)}=0.5
Y
1
^
^
{número de observaciones con r; > á F^ ' (0.5}}
^x(r.lcs)=0.5
n ;^,
'
n
Esta última igualdad, evidentemente, se verifica si á= Mediana {r; } l F^ ' (0.5}.
Un argumento similar combinado con una definición mós amplia de estimadores
M de escata ( ver Huber, 1981) se aplica en el caso en que n es impar.
Estimadores 1'VI de Dispersián
Supongarnos ahora que (y; , x; ), con x; E RP, satisfacen el madelo
y;=g(x;, 8} +aE;
dande g es una función que podemos supaner conocida, por simplicidad. Por
ejemplo, g(x^ , 9} = x; ^ o g{x; , 9} = e X'^ ^ I{1 + e X "^ e}. EI parámetro c^ representa la dispersión de los residuos
r; (9) = y; - g (x; , 8},
n
i = 1, . . . , n
n
[11J
n
Si 6 es un estimador de 8, entonces r; = r; {8) - y; - g(x; , e) son los residuos estimados y el estimador M de dispersión se defíne como la solución s de la ecuación
n ^ x ^ s / b
[12]
H^^rtM^^c^io^v ttc^Ht^s'r^t^
Martin y Zamar (1993) consideran el problema de estimación minimax en la
clase de estimadores M de dispersión cuando g(x; , E^) es constante (modelo de
posición y dispersión). La extensión de estos resultados al caso general podría
ser de cierto interés.
Estimadores S de Regresi^Sn
Sea r^ (t )= y; - g(x; , t), donde t E R P varía libremente, y sea S( t) el estimador M de escala de los números r; (t), i= 1, ..., n. Esto es, S(t) es la solución
en s de la ecuación ^12] con r; = r; (t ). EI estimador S de regresión se define
^
ahora como el vector 8„ que minimiza la escala S(t). Esto es, 8„ satisface la desigualdad
^
S( t)> S {8„ ),
para todo t E R p
Ademés, el estimador S de dispersión, á, se define simplemente como
[ 13]
Cuando la función x es de la forma [9] con a =^-' (3/4) y b= . 5, entonces
S (t) = Mediana {r; (t)}
y el estimador S de regresión en este caso minimiza la mediana ( en lugar de la
media) de los valores absolutos de los residuos. Un estimador muy parecido
que tiene la propiedad de minimizar la mediana del cuadrado de los residuos
fue definido por Rousseeuw ( 1984) y designado con las siglas LMS (least median ©f squares). '
EI cáiculo de estimadores S en forma exacta es un problema numérico muy
complejo, puesto que uno debe encontrar el minimo global de una función no convexa. Rousseeuw y Leroy (1987) proponen un algoritmo basado en sub-muestrea
que praporciona una solución aproximada en el caso del estimador LMS. En lugar de considerar todos los valores posibles de t, una se concentra en el conjunto finito t,, ..., tM de vectores que ajustan exactamente grupos de p+ 1 puntos
(entonces M= n! l[(p + 1)! ( n -- p-- 1)!]). Algoritmos anélogos también pueden
utilizarse para calcular aproximadamente estimadores S. Observemos que para
cafcular S(t^ ) debemos resolver la ecuación no lineal [12] y, cuando M es grande, el tiempo computacional requerido puede ser prohibitivamente alto. Afortunadamente, S(t^ ) necesita ser calculado en promedio /og (M) veces, únicamente cuando
1
r; ( tk )
ñ ^ x * < b
s
[14]
H.^^t a^ i»s^r^c;^ r:s^AVC^i..a
dande
s* -- min (s^, ..., sk _^}
y s^ es la solución de [12j con r, = r; {t^ ).
Estimadares Tau de Regresián
Desafortunadamente, los estimadores S de regresión no pueden ser simultáneamente robustos y eficientes bajo modelos narmales. Si la función ^ se escoge de manera que b(x) = 1/2, el correspondiente estimador S será robusto
(BP (x) = min {b (x), 1 -- b(x)}), pero la eficiencia bajo modelos normales será
rnuy ba^ a. La única manera de alcanzar alta eficiencia es usando una función ^
con b{^) grande (cerca de uno) y, por lo tanto, el correspondiente estimador no
será robusto.
Los estimadores Tau de regresión (así como los estimadores MM de regresión) fueron definidos con el objeto de alcanzar eficiencia y robustez simultáneamente. Sea S(t ) un estimador de escala de los residuos r; (t } y sea p una
función con !as mismas propiedades i)-iv} de x. E! estimador Tau de regresión
se define por !a propiedad de minimizar !a siguiente medida de la escala de !os
residuos r^ ( t }:
r; {t}
^
(t} = s^ (t} n^ P S t
(}
[15]
^.a idea intuitiva que motivó la definición de estas estimadores es !a siguiente: supongamos que !a función p es aproximadamente cuadrática cerca de cero.
Si fos residuos tipificados r; (t ) l S( t ) son relativamente pequeños, entonces
S^{ t) p{r; { ^t )! 5( t}) = r,? ( t) y!a medida de escala ^( t} no será muy diferente
de la función cuadrática ^ r;2 (t }. Por otro lado, si r; ( t )/ S(t } es grande, entances la influencia del punto i es reducida.
Por lo tanto, los estimadores Tau serán aproximadamente eficientes cuando
los datos son aproximadamente normaies y resistentes a la presencia de outlíers, supuesto que !as funcianes ^ y p sean escogidas convenientemente. Por
ejemplo, si x y p son de la familia bi-cuadrada propuesta por Tukey, los valores
apropiados de las constantes ci y c2 de ^ y p para alcanzar punto de ruptura de
1/2 y 95°lo de eficiencia san 1.^4 y 6.4, respectivamente.
ESTI^IA('1()N R()Bl'S"1`A
^i ^ y
Estimadores M de Regresión can Dispersión General
Sea r; (t ) definido como antes y sea ^s un estimador de la dispersión de los
residuos r; (^) (por ejemplo, [13]). EI estimador M de regresión con función de
pérdida p(definida como en la sección anterior) y estirnador de dispersión á, se
define por la propiedad de minimizar en t
r; (t)
1
n ^P^ á I
[16]
Cuando á está dada por [13] se obtiene el estimador MM (estimador M de regresión combinado con un estimador M de dispersión). Yohai ( 1987) probó que en
este caso el punto de ruptura está completamente determinado por la elección
de la función x y que la eficiencia bajo errores normales está completamente
determinada por la elección de la función p. Por lo tanto, estos estimadores pueden ser simultáneamente robustos y eficientes.
Si x y p son de la familia bi-cuadrada propuesta por Tukey, los valores apropiados de las constantes c1 y c2 de x y p para alcanzar punto de ruptura de 1/2
y 95% de eficiencia son 1.04 y 4.7, respectivamente.
Punto de Ruptura, Sensibilidad y Sesgo Máximo
Martin, Yohai y Zamar (1989) probaron que el estimador LMS es aproximadamente minimax entre todos los estimadores M de regresión can escala general. Yohai y Zamar (1993) probaron que esta propiedad minimax se extiende a la
clase de estimadores que dependen únicamente de los residuos (esto excluye
estimadores que reducen la influencia de puntos con alto leverage).
EI punto de ruptura de estos estimadores es independiente de la dimensión
p d e x.
La función de sesgo máximo B(E) de los estimadores de regresión con dispersión general sólo se conoce para el caso de los estimadores S y cuando la
distribución de x bajo el modelo central es elíptica ( ver Martin, Yohai y Zamar,
1989). Yahai y Zamar ( 1993) muestran que
B(>~) =y^+ o(^}
en el caso de estimadores M de regresión con dispersión general. Este resultado no requiere la hipótesis de que x tiene distribución elíptica bajo el modelo
central.
Fs^rf^^^^s^ric^t^ t^s^,^NC^^..^
4.
ESTIMADQRES DE REGRESfON CON INFLUENCIA ACOTADA
Estos estimadores fueron introducidos con el objeto de limitar la influencia
no solamente de outliers, sino también de puntos con alto /everag^e. En general,
son definidos implicitamente por la ecuación
1 ^ ^ r' (tk ) , (^ x. ^^ x.
n
'
'
s*
^
^
donde ^^ x ^^2 = x' ^ r' x y donde ^ es un estimador robusto de la matriz de covarianzas de x. La funci+án r^ (r, x} se supone: i) continua; ii} impar y no-decreciente en r; y iii) acotada, con sup r X r^ {r, x)= 1.
Todas las funciones ^ propuestas hasta ahora son de la forma
^ (r, x) = y! (rv(x)) w(x)
donde la función y^r es como las de los estimadores M de posición. Los estimadores de influencia acotada se obtienen escogíendo la función w o ia función v
con la prapiedad que sup w {x } ^( x^^ <^ o sup v (x ) ^^ x^(<^, Este es el caso
con los estirnadores propuestos por Mallows y por Andrews (ver Hill, 1977) que
tienen v (x )= 1 y w( x )= 1, respectivamente. Hill y Ryan (ver Hill, 1977) propusieron usar w{x )- v{x ), y finalmente Schweppe (ver Merril! y Schweppe, 1971 }
sugirió tomar v(x )= 1/ w(x ), con la idea de que los puntos con valores de (( x I I
grandes pero que satisfacen el modelo apropiadamente no vean su infiuencia limitada. Los estimadores propuestos por Huber (1973} tienen w(x )= v(x ) = 1, y
por lo tanto no tienen influencia acotada.
Estas estimadores son también Ilamados estimadores M generalizados (estimadores GM, usando las siglas en inglés} y se pueden calcular usando el método de Newton y Raphson. Antes de poder calcular estos estimadores, sin embargo, debemos
contar con estimadores robustos de á y de ^. La estimación ron
busta de ^ irnplica problemas nurnéricos muy serios que pueden resoiverse, al
menos aproximadarnente, usando métodos de re-muestreo similares a!os descritos en la sección anterior. ^a estimación de á, por otro lado, tiene que basar^
r;
{H)
y, por lo tanto, se requiere conse necesariamente en residuos estimados
^
tar con un estirnador robusto 8.
A diferencia de los estimadores de regresión descritos en la sección anterior,
la eficiencia de los estimadores GM depende de la distribución conjunta del vector de variables independientes x. Por ejemplo, estimadores ^M que en principio disfrutarian de una eficiencia del 95% cuando x tiene distribución normal
f:S"i'IMAC`1ON ROHI.'STA
^41
multivariante pueden resultar muy ineficientes si la distribución de x no es normal {ver Maronna, Bustos y Yahai, 1979). Notemos que mientras la hipótesis de
normalidad de los errores s^; bajo el modelo central puede parecer razonable, la
suposición de que x es normal multivariante bajo el modelo central puede ser injustificada en muchos casos.
Punta de Ruptura, Sensibilidad y Sesgo Máximo
A diferencia de los estimadores de regresión descritos en la sección anterior,
el punto de ruptura, la sensibilidad y la función de sesgo máximo de los estimadores GM depende de la dimensión del vector de variables independientes x
(ver Martin, Yohai y Zamar, 1989). A pesar de que, en general,
BGM (E) = ^^ ^ + O (E)
esto es, la función de sesgo máximo se comporta linealmente cerca de cero,
esta función (y el punto de ruptura) se deterioran rápidamente cuando la dimensión de x crece. Un punto de ruptura de 1/2 y un deteriora menor de la función
de sesgo máximo puede conseguirse calculando una sola etapa en el algoritrno
de Newton y Raphson, a partir de un estimador inicial 8 con punto de ruptura 1/2
y función de sesgo máximo de orden mayor o igual a 1/2 cerca de cero (ver
Simpson y Yohai, 1994). Estimadores GM calculados de esta forma han sido
propuestos recientemente por Simpson, Ruppert y Carroll (1992) y por Caakley
y Hettmansperger (1993).
5.
CALCULO DE LA FUNCION DE SESGO MAXIMO Y SUS DERIVADAS
En esta sección ilustraremos el cálculo de la función de sesgo máximo B{^)
en el caso sencillo del modelo de posición pura (dispersión conocida). También
mastraremos cómo se puede derivar el estimador M de posición con sesgo minimax e ilustraremos la derivación de aproximaciones lineales y cuadráticas para
B (E) .
Modelo de Posición Pura
Este es un modelo muy simple y será usado para ilustrar cómo obtener la
función B(^) y sus aproximaciones cerca de cero. EI modelo paramétrico central
está dado por
E^:S"iAUiS"1^IC`A f^Si'A!^f()1.r1
donde Fo está completamente especificada y es conocida (por ejemplo, F^ _
^ N (q,1)) y las observaciones Y,, ..., Y^ se supanen independientes e idénticamente distribuidas con distribucián F^^^.
Estimadores M
Los estimadores M de posíción fueron definidos por Huber (1964) como la
solución de la ecuación
dande yl es una función no decreciente, impar y acotada. Por ejemplo, la famosa función ^.^r de Huber:
si (y^<c
W H {Y ) = Y^
= signo (y } c,
si^yj>c
[^ 8]
donde c >_ Gl es una constante que puede tomarse igual a 1.345 si se desea una
eficiencia del 95% en el caso normal.
Sea
^^,(t, F) =-EF{yf(Y-t)}
[19]
Huber ( 1964, 1981) prueba que, si existe un único punto ^{F) tal que la función
^.^, (µ (F}, F} ! 0
entonces el estimadar M, µ„ = µ(F„ }, converge casi seguramente a µ(F}, esto es,
µ {Fn ) -^ ^ (F),
a.s. [F]
[2qj
Además, si ^,^, (t, F) es cont^inuamente diferenciable en un entorno de µ(F} y si
^.^, ( µ(F), F) ^ q, entonces µ(F^ ) es asintáticamente narmal con varianza asintótica
All(yf, F}=
EF { y^2 ( Y- µ (F)}}
^
[(d / dt) ^,^, ( µ (F), F)]2
{21 ]
ES'T'IMAC'IC.)l^ ROBUSTA
^4 ^
La función gw ( t)=^.^, ( t, Fo) juega un papel importante en el cálculo de B^, (^).
Usando la simetría de Fo y y, se verifica fácilmente que g^, (t ) es impar, estrictamente creciente y g^, (t) > 0 para todo t> o. Además,
^
9,^ ( t ) _ -EFo ^ ( Y - t ) _ --
^
lV (Y - t ) fo (Y ) dY
^
-0
4^(Y)[fo(Y-t)-fo(Y+t)^dY
donde [fo (y - t)- fo (y + t)] > O para todo par (y, t) con y> O y t> 0.
Sea F =(1 -^) Fo + E H. Por definición de µ( F),
^w(µ{F)^ F)=(1 -E)gW(µ(F))+E^,W(!^(F), H}=0
De aquí se sigue que
9',^(µ(F))=_`[^/(1 -E)^^^,(µ(F)^ H)=[^/(1 --E)^ EH^(Y--µ(F))
^[E/(1 -^)]E^,^(Y-µ(F))=[£l(1 -^)lV^(°°)
Usando la monotonía de g^, (t } concluimos que el sesgo máximo del estimador M
de posición con score yr,
B^, (E) = sup µ (F),
FE
f̀t.
satisface la ecuación
9',^ (B^, (E)) _ [E / (1 -- ^)] ^ (°^)
[22]
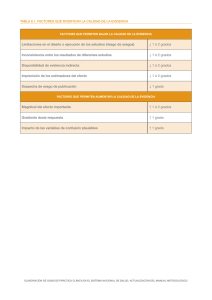
En la figura 1 presentamos las curvas de sesgo máximo de la mediana y del estimador de Huber con c= 1.345 y eficiencia del 95%. Observernos que la curva de
la mediana (línea Ilena) es uniformemente menor que la del estirnador de Huber (línea quebrada). En la sección siguiente se muestra que, en realidad, la mediana es
el estimador minimax de posición.
^4^
^STAE)tSTIC'A ^:SPA?^JC)LA
Figura 1
SESGO MAXIMO DE LA MEDIANA (iínea iiena) Y DEL ESTIMADOR DE HUBER
CON o - 1 .345 {línea quebrada)
2.5
2.0
1.0
^.5
fl.0
0.0
0.1
a.2
0.3
o.a
0.5
Epsilon
Estimador M de Posición de Sesgo Minimax
Supongamos, sin p^rdida de generaiidad, que ^ (^) = 1. Se deduce fácilmente
que si
9'^^. (t) ^ 9',^, (t),
d t>_ 0
8,^^ {E) <_ Bw2{E}
b' ^ >_ 0
entonces
Puesto que la función de score de la mediana es y^Med;a» ( t)= signo ( t) se sigue
inmediatamente que (usando que [fo (y- t)
gw ( t ) ^ g`^,^^;^^ (
- fo (y +
t}] ? 0}
t ) _ ^ _ [ ta (Y - t ) -- fo (Y + t ) ] dy = 2 Fo { t } -- 1
Por lo tanto,
B^ (£^ C ^^Median
^ ^ ^ O
(^^
ES"T'IMA(^'IC}N ROBl`STA
^45
y la mediana minimiza el sesgo máximo (es minimax) en la clase de los M-estimadores de posición.
Usando un método de prueba muy ingenioso (que no requiere el cálculo de
las funciones de sesgo máximo), Huber (1964) obtuvo un resultado aún más general: la mediana es minimax en la clase de todos los estimadores de posición T
que tienen !a propiedad
T(Y^ +b, ..., Y^+b)= T(Y^, ..., Y^)+b
Desafortunadamente, el método de Huber no se puede aplicar a otros modelos uniparamétricos (por ejernplo, escala o dispersión) ni multipararnétricos
corno posición multivariante y regresión. Sin embargo, el método de prueba descrito aquí sí puede aplicarse con éxito en otros modelos uniparamétricos y multiparamétricos. Ver, por ejemplo, Martin y Zamar (1989, 1993a y 1993b) y Martin,
Yohai y Zamar (1989).
Sensibilidad a Contaminaciones y Aproxirnaciones de Segundo orden
Naturalmente, la función de sesgo máxirno B^, (^) puede aproximarse cerca
de cero usando, por ejemplo, una expansión de Taylor de segundo orden:
2
B^ (E) = Y; (W) £ + ^2 (^) ^ + o (E2)
2
Observando que g^, (t )_
^
^
[23^
^r (y ) fo ( y+ t) dy , se obtiene
^
9w(^)_
^
^ {Y ) f^ (Y ) dY
Y
^
9'';^ (^) =
^
^ (Y ) f^' (Y ) dy = 0
Diferenciando dos veces los dos lados de [23] con respecto a^ y poniendo ^= o,
obtenemos
0
9;^(^)
r:s^rA[^is^ric^A ^-.^^Ar^c^t.a
Y
Y^ _ !g W (p ) _
9W (0)
Por lo tanta, ^23] puede escribirse com©
^
Bw tE} _ ^ ^
^ ^
^ ^ tY ) fo
£ ^ ^ + £) + Q ^£ 2)
(Y ) dY
EI factor
^ 4^ (Y } f© (Y ) dY
se obtiene también como resultado dei siguiente procedimiento: primero se ca!cula e1 iimite
lF(y, yf) = lim
E--^o
,bµ({1 -£) Fo+^Sy)
£
(donde Sy es una contaminación de masa uno en y} y luegc^ se calcula el supremo
^
n
y* (8) = sup iF (y, 9)
Y
Hampel (1968) conjeturá que
Be(£}^y*£
Noternos que debido al orden en que ei f imite y ei supremo se aplican en e1
cáiculo de y*, en general,
Aunque no existe una prueba formal de este hecho, y* _^y1 en todas los casas
en que B^, (^) es aproximadamente lineal cerca de cero, esto es, cuanda
8,^ (^) = C ^ + o {^)
E:STIMAC'1ON kOHUS'TA
En la figura 2 comparamos las aproximaciones lineat (línea de puntos) y cuadrática ( línea quebrada) en el caso del estirnador de Huber con c= 1.345. Observamos que la aproximación lineal
B,^(^) -
c
2^^ (c)-1
^
es ampliamente superada por la aproximacián cuadrática
B (E) ^
`^
c
2^(c)-1
^ (1 + ^)
También notamos que la aproximación cuadrática es muy buena para valores
de ^ menores que .20.
Figura 2
APROXIMACION LINEAL ( línea de puntos) Y CUADRATICA (línea quebrada)
A LA FUNCION DE SESGO MAXIMO (línea Ilena)
5
4
3
2
1
0
0.0
0.1
0.2
0.3
Epsilon
0.4
0.5
E^S'TAUIS`T'1C`A E5F'A!VC)I.A
fi.
COMENTARIt^S FINALES
Aunque ya han transcurrido treinta años desde el inicio de fa teoria cuantitativa de robustez can el trabajo pionero de Huber (1964), esta teoría no está
completada, ni mucho menos. Las curvas de sesgo máximo de estimadores robustos de regresión aún no se conocen en la mayoría de los casos irnpartantes
(por ejemplo, en el caso de los estimadores MM y T). En los pocos casos en que
esta curva se conoce (estimadores S y estimadores GM) las resultados son parcialmente satisfactorios, puesta que sólo valen bajo condiciones restrictivas. En
el caso de los estimadares S debe asumirse que la distribución conjunta de las
variables independientes es esférica. En el caso de los estimadores GM debe
asumirse, adem^s, que la dispersián de los residuos y que la matriz de covarianzas de las variables independientes son conocidas. La función de sesgo máximo de estimadares robustos de la ordenada al Origen no se conoce aún en
.
ningun caso.
C7tra cuestión importante es que la curva de sesgo máximo captura sbio uno
de los dos aspectos irnportantes del concepto de robustez, el de la estabilidad.
EI otro aspecto importante es el de la eficiencia bajo el modelo y en sus inmediaciones. Desde ese punto de vista, la teoría de sesgo minimax sin condiciones
laterales de eficiencia está incompleta. Puede considerarse como una teoría de
estabilidad pero no como una teoría global de robustez.
•
REFERENCIAS
. (1993): «A bounded influence, h'rgh
breakdown, efficient regression estimator», J. Amer. Statist. Assoc., 88, 872880.
CC}AKLEY, W. C., y HETTMANSPERGER, T. P
HAMPEL, F. R. {1968): «Contributions to the theory of robust estimation», Ph. D.
thesis, University of Galifornia, Berkeley.
(1971 }: «A general qualitative definition of robustness», Ann. Math. Statist.,
42, 1$87- ^1896.
(1974): «The influence curve and its role in robust estimation», J. Amer.
Statist. Asscac., 69, 383-393.
Hi^^, R. W. (1977): «Robust regression when there are outliers in the carriers»,
Unpublished Ph. D. dissertation, Harvard University, Dept. of Statistics.
E^STIMAt'ION R(:)Bl.!STA
i49
HUBER, P. J. (1964}: «Robust estirnation of a location parameter», Ann. Math.
Statist., 35, 73-101.
-- (1973) :«Robust regression: Asymptotics, conjectures and Monte Carlo»,
Ann. Statist., 1, 799-821.
-- (1981) : Robust Statistics, Wiley, New York.
LI, B., y ZAMAR, R. H. (1991): «Min-max asymptotic variance when scale is unknown» , Statist. and Probability Letters, 11, 139-145.
R. A. (1981): «Robust M-estimators of multivariate location and scatter», Ann. Statist., 4, 51-67.
MARONNA ,
MARONNA, R. A.; BusTOS, o. H.., y YoHAI, V. J. (1979): «Bias- and efficiencyrobustness of general M-estimators for regression with random carriers», en
T. Gasser y M. Rosemblat (eds.), Smoothing Techniques for Curve Estimation, Springer-Verlag, New York.
MARTIN ,
R. D.; YoHAI, V. J. , y ZAMAR , R. H. (1989): «Min-max bias robust regression», Ann. Statíst., 4, 1608-1630.
MARTIN, R. D., y ZAMAR, R. H. (1989): «Asymptotically min-max bias-robust M-estimates for positive random variables», J. Am. Statist. Assoc., 17, 494-501.
-- (1993a): «Efficiency-constrained bias-robust estimates of location», Ann.
Statist., 1, 338-354.
(1993b): «Bias-robust estimates of scale», Ann. Statist., 2, 991-1017.
MERRILL ,
H. M.,
y SCHWEPPE ,
F. C. (1971): «Bad data supression in power sys-
tem static state estimation», IEEE Trans. Power App. Syst., PAS-90, 27182725.
RoussEEUw, P. (1984): «Least median of squares regression», J. Am. Statist.
Assoc., 79, 871-880.
RoussEEUw, P., y LEROY, A. M. (1987): Robust regression and outlier detection,
Wiley, New York.
RoussEEUw, P., y YoHAI, V. J. (1984): «Robust regression by means S-estimators», en J. Franke, W. Hardle y R. D. Martin (eds.), Robust and Nonlinear
Time Series Analysis. Lectures Notes in Statistics, 26, Springer, New York,
256-272.
SIMPSON, D. G.; RUPPERT, D., y CARROLL, R. J
. (1992): « On one-step GM estima-
tes and stability of inferences in linear regression», J. Am. Statist. Assoc.,
87, 439-450.
SIMPSaN, D. G., y YoHAI, V. J. (1993): «Functional stability of one-step GM estimators in linear regression». Unpublished manuscript.
F^sr^[^is^r^c^A FsPAÑC^^.A
^5()
YoHA^, V. J. {1987): « High breakdown point and high efficiency robust estimates
for regression», Ann. Statist., 15, 642-656.
YOHAI, V. J., y MARC}NNA ,
R. A. (1979) : «Asymptotic behavior of M-estimators for
the linear model», Ann. Statist., 7, 258-268.
YOHAI, V. J., y ZAMAR ,
R. H. (1988): «High breakdown point estimates of regres-
sion by means of the minimization of an efficient scale», J. Amer. Statist.
Assoc., 83, 406-414.
(1992}: «Optimally bounding the gross error sensitivity of unbounded influence M-estimates of regression», Tech. Rep. 92-44, Departamento de Estadistica y Econometría, Uníversidad Carlos 111, Madrid.
(1993}: t^A minirnax property af the least a-quantile estimates», Ann. Statíst.,
21 , 1824-1842.
^AnnaR, R. H. {1992): «Bias robust estimation in orthogonal regressian», Ann. of
Statist., 4, 1875-1888,
R4BUST ESTIMATION
SUMMARY
The present paper presents some recent approaches of the robust estimation theory, in particular the results in the area of maximum bias minimization. A description is made of some regression robust estimators and the definition of maximum bias curve is introduced, The relation between thís curve and the sensítivity to gross
errors is discussed. These concepts are explained in the case of
simple position and dispersion models.
Key Words: minimax estirnators, maxirnum bias, sensitivity to pollutíons.
AMS Classificati©n: 62Jxx, 62H 12.
^^.5'fIMA('IOti ROBl SIA
CO MENTARIO S
ANTONIO CUEVAS
Universidad Autánoma de Madrid
La teoría de la robustez ha conocido, al igual que otras muchas disciplinas
científicas, una época de auge seguida de un período de relativo estancarniento
que, con una visión positiva, podría considerarse como una crisis de madurez.
En la actualidad, la teoría y la práctica de la estadística robusta se desarrollan a
un buen ritmo.
Los trabajos de Rubén Zamar sobre sesgo minimax son un buen exponente
de esta recuperación.
Es un honor para Estadistica Española contar con un artículo invitado de
este autor, componente destacado de la excelente escuela argentina de estadística robusta creada en torno a Víctor Yohai (Graciela Boente, Oscar Bustos,
Nélida Ferretti, Ricardo Fraiman, Ricardo Maronna...).
Mi comentario está, inevitablemente, sesgado por mi experiencia personal
sobre el tema y se dirige hacia la fundamentación maternática de los conceptos
de robustez, con mayor énfasis en algunas ideas que rne parecen especialrnente atractivas. Me interesa también destacar las relacianes de la estadística robusta con otros campos de la investigación estadística o maternática, ya que, en
mi opinión, el valor de una teoría está muy relacionado con su capacidad para
«salir de sí misma» e interaccionar con otros temas.
En beneficio de una mayor claridad dividiré mi discusión en apartados.
1.
Funcionales estadisticos
^os desarrollos teóricos en estadística robusta han contribuido a popularizar
entre los investigadores la noción de estimador considerado como restricción de
F.^r.•>t^iti^ic^r^ ^^.^t}}^,!^t>i.f^
un funcional (definido sobre el espacio de funciones de distribución) al conjunto
de las distribuciones empiricas. Esta idea no es nueva, ya que está implícita en
la noción de consistencia propuesta por Fisher en los años veinte (y mencionada por ^amar en la introducción del artículo}; sus implicaciones estadisticas se
desarrallan con detalle por primera vez en el clásico trabajo de von Mises
(1947). Sin embargo, la explotación sistemática de este atractiva «enfoque funcional^^ no se ha generalizado hasta los años setenta, coincidiendo con el desarrollo de la estadística robusta. Así, la manera natural de definir y estudiar los Ly los M-estimadores es mediante funcionales estadísticos. Las propiedades de
difPrenciabilidad de estos funcionales prop©rcionan una metodologia general
para estudiar la distribución asintótica de los estimadores asociadas [ver, por
ejemplo, Fernholz (1983}]. EI aspecto que me interesa destacar aquí es, no obstante, que la metodología basada en la diferenciación de funcionales ha demostrado ser útil en otros desarrollos estadisticos, no directamente vincufados a la
robustez; por ejemplo, el trabajo de Parr (1985) proporciona una ele+gante y sencilla aplicación al estudio de las condiciones de validez asintótica del bootstrap.
Gill (1989) utiliza métodos de diferenciación funcional en estimación no paramétrica y, en particular, extiende a este cantexto el clásico «método delta» para
obtener distribuciones asintóticas de estimadores.
2.
Robustez cualitativa
Rubén Zamar menciona este concepto de manera muy esquemática, ya que
está quizá un poco apartado de su linea expositiva general. Por mi parte, sólo
quiero cornpletar y matizar con brevedad su comentario.
Como señala ^amar, en el caso de las estirnadares generados por un funcional, la continuidad de éste es la condición suficiente natural para ia robustez cuaiitativa. Esto se sitúa en la linea, comentada en el punto anterior, de traducción estadistica de propiedades analiticas del funcional. Un paso más en esta dirección puede encontrarse en Cuevas y Ramo (1993}, donde se demuestra que la continuidad
uniforme (respecto a la distancia bounded Lipschitz) es una condición suficiente
para la robustez cualitativa de ias aproximaciones bootstrap a la distribución en el
muestreo: se trata, por tanto, de una aplicación na pararnétrica del concepto. En
este mismo trabajo pueden encontrarse algunas referencias interesantes sobre
otras extensiones de la noción de robustez cualitativa. Por ejernplo, Boente et al.
(1987) estudian la robustez cualitativa en el caso de observaciones dependientes.
Respecto al significado de la robustez cualitativa, Huber (1981, p. 10) señala
que, desde un punto de vista matemático, este concepto impone un requerimiento de continuidad análogo a la noción de estabilidad en un sistema controlado par una ecuación difereneiai ordinaria. Se trata, por tanto, de una idea básica muy arraigada en diferentes contextos.
F:ST'11^1A('IOti KC)F3l1S.i_•i
^5 i
A propósito del comentario de Zamar «... esta teoría (...) no permite comparaciones dentro de la clase de estimadores que son cualitativamente robustos»,
quisiera matizar que, en cierto modo, el punto de ruptura [ver, por ejemplo, Huber (1981)] es una noción complernentaria que cumple la función de cuantificar
la robustez. EI punto de ruptura es, en términos intuitivos, !a máxima cantidad
de contaminación en la distribución subyacente que puede tolerar un estimador
de manera que todavía proporcione alguna información sobre el parámetro de
interés. Creo que este concepto no ha sido aún estudiado con la profundidad
que merece. Hay varias cuestiones, como la definición de aproximaciones
rnuestrales satisfactorias o la extensión a diferentes contextas (incluyendo la inferencia bayesiana), que son aún, básicamente, problemas abiertos.
3.
La curva de influencia
Este es, sin duda, uno de los conceptos más populares y fecundos dentro de
la teoría de la robustez. De hecho, es el eje central del libro de Hampel et al.
(1987) sobre estadística robusta. ^as observaciones que siguen pretenden simplemente completar los comentarios de Rubén Zamar sobre el tema.
Desde el punto de vista matemático, la función de influencia es para un funcional estadístico lo que el vector gradiente es para una función real de n variables. La función de influencia proporciona el término lineal de los desarrollos de
Taylor de primer orden [ver Fernholz {1983)] que permiten probar la normalidad
asintótica para los estimadores definidos como restricción de un funcional diferenciable. Coma consecuencia, la varianza asintótíca aparece en estos casos
como la media del cuadrado de la función de influencia. Este hecho puede utilizarse para estimar la varianza asintótica, supuesto que se dispone de un estimador adecuado de la curva de influencia. EI estimador más popular es la así
Ilamada curva de sensibilidad. Curiosamente, el estudio de sus propiedades
asintóticas permanece casi inédito; una referencia reciente sobre este tema es
Cuevas y Romo (1995).
Recordemos, por último, que la curva de influencia tiene una interesante relación con el método de remuestreo denominado jackknife [ver Efron (1992)]; en
particular, se puede obtener una aproximación muestral de la curva de influencia como subproducto de los cálculos necesarios para obtener la versión jackknife de un estimador.
4.
Estirnadores de mínima distancia
Los ejemplos presentados en el artículo se centran en modelos de posición/escala y regresión. En este tipo de modelos los estimadores considerados
E^^.:4^I ^1[)f:^^t^l(^.^ ^-.S(',^\ti'O1^,^
{principalrnente los de tipo M) ocupan, sin duda, un papel protaganista. Hay, sin
embargo, otras situacianes (por ejemplo, Ios modelos paramétricos de mixturas)
en que resulta útil considerar !os estimadores Ilarrtados «de mínima distancia»
que, bajo condiciones bastante amplias, son robustos. EI trabajo de Parr y
Schucany (1980) es una referer^cia clásica sobre el tema.
La forma general de estos estimadores es:
^
8„ = argmin ó (F,,, F^),
donde F^ es la distribución empírica, F^ es el modelo teórico y S es una medida
de discrepancia (no necesariamente una métrica) entre funciones de distribu-
ción
Una idea bastante natural {aunque, sorprendentemente, no estudiada hasta
ahora) es considerar una versión «suavizada» de la anterior definición en la que
FH es reemplazada par la densidad f^ (cuando esto tenga sentido} y F^ se reemplaza por un estimador no paramétrico (de tipo núcleo, por ejemplo) de fe. La
discrepancia b se cambiaría entonces por una distancia natural (por ejemplo, L^
o L2) entre densidades. En Cao et a!. (1995) se analizan algunas aspectos teóricos (consistencia, normalidad asintótica, robustez) y prác#icos (comparaciones
por simulación} de esta modalidad de estimadores de mínima distancia. Los resultados son, en general, bastante alentadores.
Comentario final: un asunto de relaciones púbiicas
Ctuisiera concluir estas líneas con una reflexión acerca de un asunto que tiene, según creo, cierta importancia práctica: la creciente disponibilidad de medios computacionales baratos y eficientes ha estimulado la aparición de una amplia demanda de análisis estadísticos por parte de un público usuario formado
mayoritariamente por no profesionales de la estadística. Este público, a su vez,
contribuye a orientar la investigación planteando sus propias demandas, na
siempre fáciles de satisfacer. Una consecuencia de este hecho es que cualquier
teoría estadística que no consiga, en alguna medida razonable, comunicarse
can los usuarios y«vender su producto» está condenada a mantenerse en el
g^hetta de las revistas especializadas y, quizá, a desaparecer. No creo que ésta
sea exactamente la situación de la estadística robusta, pero sí considero que
los expertvs en este tema han tenido mucho más éxito en la elaboración de una
teoría sólida y elegante que en facilitar su acceso al público usuario. Por ejemplo: hay actualmente centenares de estimadores robustos exhaustivamente estudiados en diferentes contextos, pero los especialistas no parecen ponerse de
acuerdo en seleccionar un reducido número de ellos para su implementación en
!os paquetes estadísticos más usuales. Hay, asimismo, algunos conceptos
t:ti'1'Iti1A(^1Oti ROfil'^"^ A
^55
como el de punto de ruptura o el de curva de influencia que tienen una gran potencialidad desde el punto de vista aplicado: una vez más, su popularización dependería de su presencia en el software comercial. Se trata, en último términ©,
de un problema de divulgación que, por otra parte, no es exclusivo de la estadística robusta.
Estoy convencido de que un investigador de la categoría de Rubén Zamar
puede hacer aportaciones muy interesantes en este sentído.
REFERENCIAS
Qualitative robustness for stochastic processes», Ann. Statist., 15, 1293-1312.
BOENTE, G.; FRAIMAN, R., y YOHAI, V. (1987): «
CAO, R.; GUEVAS, A., y FRAIMAN, R. (1995}: <tMinimum distance density-based estimation^>, Comp. Statist. & Data Analysis (en prensa).
CuEVAs, A., y RoMO, J. (1993): «pn robustness properties of bootstrap approx'rmations» , J. Statist. P/ann. lnference, 37, 181-191.
-(1995): «On the estimation af influence curve», Canadian J. Statist. (en prensa).
EFRON, B. {1992): «Jackknife-after-bootstrap standard errors and influence functions» , J. R. Statist. Soc. B, 54, 1, 83-127.
FERNHOLZ, L. T. (1983): Von Mises Calculus for Statistical Functionals, SpringerVerlag, New York.
GILL, R. D. (1989): «Non- and semi-parametric maximum líkelihood estimators
and #he von Mises method (Part I}», Scand. J. Statist., 16, 97-128.
HAMPEL, F. R. (1971): «A general qualitative definition of robustness», Ann.
Math. Stat., 42, 1887-1996.
I-iAMPEL, F. R.; RONCHETTI, E. M.; ROUSSEEUW, P. J., y STAHEL, W. A. (^ 987):
RO-
bust Statistics. The Approach Based on /nf/uence Functions, Wiley, New
York.
HusER, P. J. (1981) : Robust Statístics, Wiley, New York.
MIsES, R. von (1947): «On the asymptotic dístributions of differentiable statistical
functions», Ann. Math. Statist., 18, 309-348.
PARR, W. C. (1985): «The bootstrap: some sample theory and connectíons with
robustness» , Stat. Prob. Letters, 3, 97-100.
PARR, W. C., y SCHUCANY, W. R. (1980): «Mínimum distance and robust estimation», J. Amer. Statist. Assoc., 75, 616-624.
^^ ^ E^
F-.^^r ,tii^r^^rrc^ ^^ r-tir^,^^^v^,r.^^
ALFCrNSO GOF^UALIZA
Universidad de Valladolid
Quisiera comenzar expresando mi reconocimiento al profesor Zamar por las
importantes aportaciones realizadas en ios últimos años al campo de la estimación robusta, de las cuales una pequeña muestra es objeto de estudio y discusión en la parte f'rnal de este artículo.
EI trabajo se estructura en tres partes. Una primera parte (secciones 1 y 2)
donde, de una manera sencilla y clara, se hace una introducción a la teoría de
la estimación robusta, presentando las diferentes teorías existentes e incidiendo, sobre todo, en el compromiso estabilidad-eficiencia que representa y en las
ideas de invariancia presentes en todo problema de estimación. Este tipo de introducciones pueden contribuir a paliar la escasez de referencias a la robustez
en los textos básicos, donde cada vez se hace más necesario introducir algunas
nociones como hace, por ejemplo, Peña (1991), con las limitaciones lógicas derivadas del tipo de lector a quien va dirigido.
La segunda parte (secciones 3 y^4) presenta, de una manera escalonada y
motivada, una serie de familias de es#imadores que están mostrando un mejor
comportamiento en el intento de extender las ideas de robustez al contexto de
regresión y estimación multivariante. Esta parte tiene, sobre todo, el mérito de
ayudar a los recién incorporados al estudio de la robustez a conducirse entre
una verdadera maraña de siglas.
En la tercera parte (sección 5} es donde realmente se discuten recientes enfoques de la teoría de la estimación robusta, como se anuncia en el aóstract.
Mis comentarios se centrarán especialmente en esa parte del artículo.
Como los artícuios invitados que publica Estadística Españo/a tienen un carácter eminentemente divulgativo y, en consecuencia, parte de sus lectores probablemente no serán grandes conocedores del desarrollo de la teoría de la estimación robusta, comenzaré haciendo un breve recordatorio de las fases por las
que ha pasado dicho desarrollo que, de alguna manera, será el hilo conductor
de mis comentarios.
EI desarrollo de la teoría de la estimación robusta está marcado, a mi juicio, por los importantes .altibajos que ha experimentado. P. H. Huber (1981)
recoge muy bien en el prólogo de su libro la desconfianza inicial por parte de
la comunidad de estadisticos teóricos hasta que Ilegó el reconocimiento {años
65-75}, gracias, sobre todo, a las aportaciones de Huber (19f4) y Hampel
F:^"I^IMA('It)N R()K('tiTA
(1968, 1971, 1974), y el posterior intento de «subirse al carro de la robustez»
de buena parte de los estadísticos. La descon#ianza inicial se debió a la escasa seriedad que, desde el punto de vista maternático, parecían ofrecer las alternativas robustas, y por ahí, precisamente, Ilegó e! reconocimiento, gracias
al esfuerzo de Huber y Hampel por dar #orma matemática a las ideas de robustez, especialmente en el contexto de localización univariante. Se habían
dado los primeros pasos, pero quedaba todo el camino por recorrer: sustituir
los abundantes resultados heurísticos por teoremas, conectar rigurosamente
las distintas teorías, extender las ideas a otros contextos (regresión, estirnación multivariante...), etc.
Lamentablemente, la subida masiva de estadísticos al «carro de la robustez»
no se tradujo, salvo excepciones, en avances significativos en Ios aspectos
mencionados, sino que, más bien al contrario, se produjo una desviacíón ^^peiigrosa» hacia el análisís de datos (las publicacianes sobre robustez desaparecen
prácticamente de Annals of Statistics} sin un avance paralelo de la vertiente estadístico-matemática de los problernas, lo que vuelve a suscitar recelos en la
comunidad de matemáticos estadísticos.
Afortunadamente, en los últimos años ha vuelto a cobrar importancia el desarrollo estadístico-matemático de la Estadística Robusta, produciéndose notables avances. Entre los más relevantes están los conseguidos en la línea de
trabajo a la que pertenece el profesor Zamar, y la sección 5 de este artículo
muestra una pequeña pincelada de sus logros. Esta línea de trabajo reabre el
problema de la medición de la robustez de estimadores a partir de la curva de
sesgo máximo y la obtención de estimadores de sesgo minimax. Estos problemas estuvieron abandonados durante veinte años, a raíz de que Huber desestimara el probfema del sesgo máximo en favor del de la varianza por considerar este último como un problema más profundo. Huber resalvió el problema
del sesgo minimax en localización univariante con una demostración ingeniosa y brilfante pero basada en argumentaciones geométricas que no permiten
una extrapolación a otros contextos. Además, coma !a solucián era siempre la
mediana (para distintos tipos de entornos y para cualquier radio), Huber consideró camo t<aburrido» el problema del sesgo máximo y se pasó a utilizar simplemente un «resurnen grosero» de fa curva de sesgo máximo como es el
punto de ruptura asintótico, que tiene su antecedente en la noción análoga introducida por Hampel (1968, 1971). Incluso se establecen versiones muestrales de dicha noción, cuyas conexíones con las nociones poblacionaies nunca
se establecen de manera rigurosa y cuya utilidad real queda bas#an#e en entredicho a raíz de algunas publicaciones como, por ejemplo, la de Hettmansperger y Sheater (1992).
^5x
E-:s r.^r^r^ i rc^.> E-.:^r^,>tic^i.,^
EI método alternativo para tratar el problema del sesgo máximo que se recoge en este artículo, tiene la doble ventaja de ser extensible a otros conceptos y
de arrojar alguna luz sobre las relaciones entre las teorías minimax e infinitesimaí, por medio de la derivada de la curva de sesgo máximo y el supremo de la
función de influencia.
Existen otros enfoques, igualmente actuales, en la teoría de la estimación robusta, y se echa de menos siquiera una referencia a los misrnos en este artículo. Me refiero especialmente al artículo de Davies (1993) en ef que se defienden
posiciones de alguna manera encontradas con la línea de trabajo minimax que
se discute en este artículo y se ofrecen vías alternativas. EI articulo de Davies
contiene, entre otras cosas, notas críticas sobre robustez y optimalidad, sobre el
uso de métricas y entornos de contaminación y sobre las distintas nociones de
punto de ruptura. Davies defiende que ia estabilidad de la inferencia no se consigue obteniendo funcionales óptimos sino construyendo funcionaies con propiedades especificadas. También defiende que los estimadores óptimos son fronteras que delimitan la posible y no son utilizables para aplicaciones a datos reales, donde la único razonable es utilizar estirnadores que sean un compromiso.
Asimismo critica ios entornos de contaminación por violar el espí ritu de la robustez y, en su lugar, aboga por el uso de métricas, lo que también serviria para reconducir a sus orígenes la noción de punto de ruptura. Davies hace propuestas
de estimadores de dispersión y de regresión en la línea de «estimadores compromiso» mencionada anteriormente.
Es de reseñar, no obstante, que las críticas a la teoría minimax no son del
todo nuevas, como puede verse, por ejemplo, en Huber (1972) o en Hampel,
Ronchetti, Rousseeuw, Stahel (1986}.
REFERENCIAS
DaviES, P. L. (1993}: «Aspects of Robust Linear Regression», Ann. Statist., 21 ,
4, 1843-1899.
HAMPE^, F. R. (1968}: Contributions to the theory of robust estimation, Ph. D.
Thesis, University of California, Berkeley.
(1971 }: «A general qualitative definition of robustness», Ann. Math. Statist.,
42, 1887-1896.
(1974): «The influence curve and its role in robust estimation», J. Am. Statist.
Assoc., 69, 383-393.
F:ST'1ti1AC'1c)N R()E3l'STA
HAMPEL, F. R.; RONCHETTI, E. M.; ROUSSEEUW, P. J., y STAHEL, W. A. (1986): RO-
bust Statistics: The approach based on inf/uence functions, Wiley, New York.
HETTMANSPERGER, T. P., y SHEATHER, S. J
. (1992): ^<A cautionary note On the
method of least median of squares» , Americ. Statist., 46, 79-83.
HUBER, P. J. (1964): «Robust estimation of a location parameters^, Ann. Math.
Statist., 35, 73-101.
-(1972}: «Robust Statistics: A review», Ann. Math. Statist., 43, 1041-1067.
-(1981): Robust Statistics, Wiley, New York.
PEÑA ,
D.(1991) : Estadística. Modelos y rnétodos, vol . I, 2. ^ ed .
JULIAN DE LA HORRA
Universidad Autónoma de Madrid
Para mí es un placer esta oportunidad que me brinda Estadística Española
de poder contribuir con algunos comentarios al trabajo del profesor Zamar
sobre Estirnación Robusta, que me ha parecido interesante por muchas conceptos.
EI trabajo del profesor Zamar se centra, particularmente, en resultados sobre
minimización del sesgo máximo. Es decir, estudia el problema que se plantea
cuando se trata de encontrar un estimador que <tminimice» el «rnáximo» sesgo
asintótico, lo cual es una aplicación del principio «minimax». Mi aportación irá
dirigida a señalar la interesante aplicación que tiene también el principio t<minimax» en robustez bayesiana. Entre los dos enfoques hay semejanzas y diferencias que se pondrán de manifiesto a continuación.
Wasserman (1989) estudió el problema que se plantea cuando se quiere encontrar una región de confianza bayesiana y se tiene cierta incertidumbre sobre
la distribución a priori; en concreto, se considera como clase de distribuciones a
príori la clase de ^-contaminación alrededor de una distribución a priori central.
Obsérvese que aquí la falta de seguridad radica en la distribución a priori (no en
el modelo de muestreo), pero se formaliza de rnanera análoga (a través de !a
clase de ^-contaminación}. Una diferencia adicional es que Wasserman no tra-
^6C }
E^S^i AU1tiT1C'A E`iF'Ati()l.A
baja con estimadores puntuales, sino con regiones de confianza; en concreto,
considera la clase de regiones de confianza que tienen un contenido de probabifidad a posteriari (calculado a partir de la distribución a priori central} fijo {digamos Y,^).
EI objetivo de Wasserman es encontrar la región de confianza (dentro de la
clase indicada} que «minimiza» la «máxima» diferencia posible de contenido de
probabilidad a pQSteriorí (cuando la a priorí recorre fa citada clase de ^-contaminación). C}bsérvese el parafelismo con buscar el estimador que «minimice» el
«máxima» sesgo asintótico.
Señalemos, para acabar, que Wasserman prueba que la región buscada es
la región de máxima verosimilitud.
Este tipo de estudios ha sido continuado en De fa Horra y Fernán+dez
(1994a}, donde se consideran otras clases de regiones de confianza. En primer
lugar, se considera el conjunto de regianes de confianza con un contenido de
probabilídad a posteriori entre dos valores fiijados, pasando después a analizar
fa clase que parece más natural: {a que incluye aquellas regiones de confianza
con un contenido de probabifidad a posteriori superior a un valor ^yo y con una
medida de Lebesgue inferior a un valor lo. Pero el objetivo es siempre el mismo:
«minimizar» la «máxima» diferencia posible de contenido de probabilidad a pvsteríori. La solución a estos problemas siempre está ligada a la nocián de región
de máxima verosimilitud.
Posteriormente, en De la Horra y Fernández (1994b) se estudian estos problemas en relacián con la existencia de parámetros perturbadores.
Espero que estos comentarios hayan servido para poner de manifiesto las
semejanzas que a veces hay entre enfoques originalmente muy diferentes.
REFERENCIAS EIV LA DISCUSION
C. (1994a): «Bayesian analysis under s✓ -contaminated priors: A trade-off between rabustness and precision», J. Statist. Plan.
DE LA HORRA, J., y FERNÁNDEZ ,
lnf., 38, 13-30.
(1994b}: «Bayesian robustness of credibfe regions in the presence of nuisance parameters» , Commun. Statist. -Theory Meth., 23, 689-699.
WASSERMAN, L. {1989) :«A robust Bayesian interpretation of likelihood regions»,
Ann. Statist., 17, 1387-1393.
EST'IMAC'It)N ROHl'S"I^A
ALFONS^ GARCIA PEREZ
Departamento de Estadística
Facultad de Ciencias. UNED
EI trabajo del profesor Zamar recoge, de forma acertada, algunas líneas de
análisis de la robustez de estimadores por punto T„ que dependen de la muestra a través de la distribución empírica F„ = 1/ n^;'` , bX; ; es decir, que pueden
ser expresados de la forma T^ = T(F„ ), con T algún funcional cuyo dominio no
sólo es el espacio de las medidas empíricas, sino que, de forrna habitual, suele
extenderse a(un subconjunto de) el espacio ^(X ) de todas las medidas de
probabilidad definidas sobre el espacio muestral X.
De las líneas de análisis tratadas, el autor centra su trabajo, fundamentalmente, en la desarrollada por él y los profesores Martin y Yohai, la cual utiliza
como medida de la robustez de un estimador, básicamente, la función de sesgo
máximo,
BT (€) = sup d [ T ((1 - €) Fe + € H ), T (FA )]
H
= sup d [ T( G), 9^
G E iF
en donde
^^(Fe)={G^G=(1 -€) F^+€H, HE ^(X)}
es un «entorno» en el modefo de contaminación.
Con dicha función de sesgo máximo, BT (€), generalización de la definida por
Huber ( 1964), es posible analizar el va/or asintótico del estimador T(F„ }, en
función de la cantidad de contaminación fijada, €, permitiendo además interesantes representaciones gráficas, como la figura 2 del autor ( donde, por cierto,
cabe mencionar que la asíntota vertical corresponde al punto de ruptura €*).
Como bien dice el autor, habitualmente, esta función puede aproximarse linealmente cerca de cero de la forma
BT(€)=y*(T)•€+o(€)^y*{T)•€
siendo
y*(T)=sup^^/F(x; T)II
X
la sensibilidad a grandes errores definida por Hampel (1974).
C^:^`f A[)ISI'tC'A f-.5F':;ti()F_:^
No obstante, el análisis de un estimador debe basarse no sólo en un estudio
de su sesgo (asintótico}, sino también de su varianza (asintótica), V( T, F^ }. Parece, por tanto, razonable d+efinir una función de varianza máxíma que fuera del
tipo
VT (^) = sup d [ V( T, G}, V( T, FQ }^
G E '^^
En esta situación, sería razonable tratar de determinar también el ó ptimo en
el sentido minimax. Pero, probablemente, io más interesante, en línea con el
trabajo del autor aqu í comentado, fuera aproximar linealmente dicha funcitín de
varianza máxima
mejor dicho, su logaritmo
por la sensibilidad al cambio-devarianza k*{ T)= k*( T, F^ ), concepto i ntroducido por Peter Rousseeuw (1981)
en su tesis doctoral y más tarde generalizado por Collins (1976, 1977} y Collins
y Portnoy ( 1981).
Si esta idea #uera viable, permitiría, posiblemente, una aproximación del tipo
VT (E} ^ V ( T, FH ) • exp {^ • k * ( T, F,^ )}
es decir, que, en analogía con la aproximación a la función de sesgo máximo,
fuera k* ( T) la pendiente de la tangente en cero, ahora de la función In VT {^),
función ésta que probablemente deberia tener una asíntota vertical en el, (Huber, 1981 }, punto de ruptura +de fa varianza (asíntótica), ^**.
En esta situación, entiendo que también sería viable una aproximación cuadrática a la función de varianza máxima, corno la que hace el profesor Zamar en
su artículo con función de sesgo máximo.
Respecto a las aproximaciones, suele tomarse como regla práctica en cuanto a la vatidez de la aproximación lineal para ia función de sesgo máximo BT (^),
valores ^<_ ^* 1 2. ^,Qué ocurre con la aproximación cuadrática? ^Qué ocurriria
con las hipotéticas aproximaciones a In VT (^)?
Todo esto en lo referente a«entornos» de contaminación, pero ^se podrian
extender algunos resultados a verdaderos entornos en la topologia débil, en la
dirección seguida por Rychlik y Zielinski o Riedel?
Otra cuestión que afecta no sólo a este artículo, sino de forma bastante generalizada a la Estadística Robusta, es la relacionada con la posibilidad de evitar resultados ( totalmente} asintóticos, los cuales, en mi opinión, no son enterarnente satisfactorios. Estos, aunque simplifican notablemente el problema, en no
pocas ocasiones equiparan comportamientos de estimadores claramente diferentes cuando se emplean tamaños muestraies pequeños.
E-:S ( I;^1.^C'IC ^N ROt3l;S I:^
^ fa.i
Como la suposición de tamaños muestrales finitos resulta en muchos casos
imposible, sugiero al autor la posibilidad de aproximar la distribución del estimador T(F„ )(al menos, cuando éste sea un M-estimador) rnediante las denominadas small-sample asymptotic techniques (Field y Hampel, 1982), las cuales, utilizando palabras del propio Huber (1981, p. 48), «... parecen dar aproximaciones fantásticamente precisas hasta tamaños muestrales muy pequeños
(n=3ó4}».
Mi último comentario es de gratitud, primero, hacia el profesor Zamar por el
esfuerzo realizado al resumir de forma precisa y amena un tema tan fundamental y de tanta actualidad en la Estadística corno es el de la robustez y, segundo,
al director de la Revista por haber conseguido la colaboración de tan distinguido
especialista.
REFERENCIAS
COLLINS, J. R. (1960): «Robust estimation fo a iocation parameter in the presence of asymmetry», Ann. Statis., 4, 68-85.
(1977): «Upper bounds on asymptotic variances of M-estirnators of location», Ann. Statis., 5, 646-657.
J. R., y PORTNOY , S. L. (1981): «Maximizing the variance of M -estimators using the generalized method of moment spaces», Ann. Statis., 9, 567-
COLLINS ,
577.
FIELD, C. A., y HAMPEL, F. R. (1982): «Smali-sample asymptotic dis#ributions of
M-estimators of location», Biametrika, 69, 29-46.
HAMPEL, F. R. (1974): «The influence curve and its role in robust estimation»,
J. Am. Statist. Assoc., 69, 383-393.
HUBER, P. J. (1964): «Robust estimation of a location parameter», Ann. Math.
Statis., 35, 73-101.
(1981) : Robust Statistics, Wiley.
RoussEEUw, P. J. (1981): «New infinitesimal rnethods in robust statistics», tesis
doctoral, Vrije Universiteit, Bruselas, Bélgica.
^f^
^-;^;"i A[^15"i^lc^r^ h^F?.^Nc ^1..^^
RICARDC^ A. MAR4NNA
Universidad Nacional de La Plata y CICPBA
E1 interesante artículo del profesor Zamar trata del modelo de posición y escaia univariados y, en general, del modelo lineal con respuesta univariada. C^uisiera hacer aquí algunas consideraciones sobre el modelo lineal multivariado
Bx; + e; ,
ti- 1, ..., n}
[1]
donde y; E RQ, los e; E RQ son vectores i.i.d. con matriz de covarianzas ^, B E
RQ x p es la matriz de parámetros desconocidos, y los x; E Rp son, o bien fijos, o
b+en aleatorios i.i.d. e independientes de los e; .
En la teoría clásica se supone que los e; son normales, con lo que el estimador de mínimas cuadrados (EMC) es el de máxima verosimilitud y resulta óptimo
no sólo asintóticamente, sino también para n finito. Bajo condiciones bastante
generales, el EMC es asintóticamente normal con matriz de covarianzas
^ ^ (x^ x}-1
^2]
donde ^ es el producto de Kronecker y X E Rn X p es la matriz de las x; .
Perv cuando las observaciones (x; , y; ) pueden tener datos atípicos, el EMC
presenta todos los inconvenientes ya conocidos para el caso univariado, con el
agravante de que el carácter multidimensional de las y; puede hacer la detección
de observaciones atípicas aún más dificil. Sería entonces deseable obtener estimaáores que tuvieran: 1} alta eficiencia para e normal; 2} punto de ruptura S* alto;
3) equivariancia para transformaciones lineales de las x; y de ias y; , y^} cálculo
numérico factible. Si se quiere estirnar eficientemente todas las combinaciones lineales de los coeficientes B, la condición 3) es necesaria para la ^}.
Como muestra Zamar en su artículo, se dispone de estimadores que cumplen las cuatro condiciones mencionadas para el caso q= 1; y, por lo tanto, sería naturaf pensar en estirnar cada fiia de B separadamente usanda un estimador robusto univariado. Pero este procedimiento no sería equivarian#e bajo
transforrnacíones de las y, por lo que no sería eficiente para combinaciones lineales arbitrarias de B. Hace falta entonces otro enfoque.
En el caso q^ = 1, si bien la situación no es sencilla, se han hecho al menos
considerables progresos y se cuenta con estimadores confiables; y se puede
encarar el problema de la optimalidad. En cambio, en el caso multivariado el terreno es prácticamente virgen. EI principal interés del caso multivariado está en
seemingly unrelas aplicaciones econométricas, en particular e1 modelo SUR
E:^"I'IMAC'1(3N R()B(_!S"T^,
3f^5
lated regressions (regresiones aparentemente no relacionadas); ver Koenker y
Portnoy (1990)
y Ecuaciones Simultáneas (Maronna y Yohai, 1995a). Si bien
estos dos modelos contienen al modelo lineal multivariado como caso particuíar,
preferimos limitarnos a éste para no complicar la exposición.
Los M estimadores para este modelo son de 1a forma
n
^U^(d;)r;i0
i^ 1
n
^u^(d;)r; r;=n^
^-,
[4]
donde r; son los residuos:
r;=r; (B)=y;--Bx;
las d; son las «distancias de Mahalanobis»
=d;(B,^)=
(B)`^-^ r; (B)
C5]
y u1, u2 son funciones decrecientes.
Los M estimadores son asintóticarnente normales, con matriz de covarianzas
de la forma (??}, pero con ^ reemplazada por una matriz S que tiene la forma de
la matriz de covarianzas de un M estimador de posición multivariada. Si bien la
expresión general es complicada, para e; con distribución simétrica se reduce a
S= D-' A(D-')'
[6]
con
D=2 Eu^ (d) ee' V-' + Eu^ (d) I
y
A= E u1 ( d) 2 e e'
donde d= e' V-' y V se defi ne como
V=Eu2(d)ee'
Pero el punto de ruptura de estos estimadores es 0, pues no tienen robustez
frente a x; atípicos.
^%^
F:^`I A[)Iti`i l(^A t^.S}^:^^()[_A
Notemos que, en el caso univariado, casi todos los métodos de estimación
se basan en minimizar una medida de la escala de los r; . EI EMC minimiza la
rnedia de los cuadrados, y los estimadores de tipo S o t minimizan una escala
robusta de los residuos. En el caso multivariado, si se conociera ^, se podría
obtener un estimador robusto minimizando una escala robusta s(d ) donde d=
_(B ,^) _{d,, ..., dn }. La forma de tener en cuenta también a^ la encontró
Lopuha^ (1992) en el caso particular de posición y dispersión multivariadas, para
ef que definió T-estimadores. La extensión natural al caso general es la siguiente:
n
det ( ^) _
^ p2 (d;)}q = rnin
;= ^
[10]
bajo la condición
n
^ p1 (d; ) = n
^_,
donde p, y p^ son funciones no decrecientes y acotadas con p; {0) = 0.
Eligiendo p^ adecuadamente, se puede obtener un punto de ruptura S* arbitrariamente alto (<_ 4.5). Se puede probar (Maronna y Yohai, 1995b} que estos
estimadores son asintóticamente normales, con matriz de covarianzas de la
misma forma que los de un M estimador, donde las funciones u1 y u2 dependen
de p^ , p2 y la distribución de e.
EI cálculo numérico se puede realizar en forma aproximada usando las mismas ideas que en el caso univariado.
REFERENCIAS
KOENKER, R., y PoRTNOY, S. (1994): «M Estimation of Multivariate Regressions»,
Journa/ of the American Statistica/ Association, 85, 1060-1068.
LOPIJHA,4, H. (1992}: «Estimation of Location and Covariance with High Breakdawn Point», tesis doctoral, Technische Universiteit Delft.
MARC}NNA ,
R. A., y YoHAi, V. J. (1995a): «Robust Estimation for Simultaneous
Equations Models», presentado para publicación.
(1995a}: «Tau-estimators for Simultaneous Equations Models», trabajo en
preparaci+ón.
.ifi7
F:S^^1^1^1A('I^)ti ROfil^ti"^fA
ELIAS MORENO
Universidad de Granada
JUAN ANTONIO CANO
Universidad de Murcia
Es un placer expresar nuestra felicitación y agradecimiento al profesor Zamar por brindarnos este excelente artículo sobre Robustez Local de un procedimiento de estimación 6(^), que con tanta claridad expone. G?uede también nuestro agradecimiento al profesor Daniel Peña, editor de Estadística Española, por
brindarnos la oportunidad de comentar sobre este artículo.
No deja de ser curioso que la motivación utilizada por el autor ( motivación
que compartimos) se base en unas determinadas observaciones muestrales y
que, sin embargo, todo el desarrollo posterior dependa exclusivamente de la forma estructural del modefo considerado F^ ={F : F=(1 -^) Fo + F H, H(arbitraria)}
tales como
B^ {0) = lim sup [ 8 ((1 - ^) Fo + E H} - 6 (Fo )] / ^
F --^ 0
H
ó-EFo yr ( Y- B y^ ( E}) para el score y^.
Hay aspectos de la incertidumbre sobre 8 que la clase F^ trata de modelar
que no se hacen notar con este tipo de herramientas locales, pero que se advierten si adoptamos un punto de vista global y condicional de la inferencia.
Con esto queremos decir lo siguiente. Supongamos que estamos interesados en hacer inferencia sobre un cierto conjunto A de valores de 8(que pudiera
ser la hipótesis nula de un test), condicional a las observaciones x^, x2, ..., x^ .
Supongamos que las observaciones son i.i.d. según f (x ^ 8) _(1 - c) fo (x ^ e) +
+^ q(x ^ 6), en donde fo está fijada, 0<^< 1, y q(x ^ E^) E Q; es decir, cada observación x; proviene de fo (x ^ e) con probabilidad {1 -^) y de q(x ^ H) con probabilidad c. Q podría ser la banda
Qb={q(xl e) ^fo(xle)-b^q(xle)^f^(x^e)+s,s>o}
Q^ nos dice que la verosimilitud de 6 para el dato x; está próxima (^) a la dada
por el modelo base fo (x; ^ e).
Para las observaciones x=(x1, x2, ..., x„ ), la clase de verosimilitudes viene
dada por
^Eh ={f (x ^ e) : f(x ^ e} = n; f (x; ^ e), f(x; ^ ^) _( 1- ^) fo (x; ^
e) +^ q(x; ^ e), q E Q^ }
F-,ti I:^F)1`^ I I(^r1 F-.^F'AN()F...^1
;fa,?^
clase, por otro lado, bastante razonable y más pequeña que la considerada en
el artículo.
Supuesto que nuestra información a priori sobre 8 viene representada por
n(H), la robustez global a posteriori (o incertidumbre a posteriori) de nuestra inferencia vendría medida por
R{A j x}=
sup
f E `j.s
P^ {A ^ x}-
Pf (A ^ x)
inf
f E `^^_^
conPtn(A^x)=^Af(x^H)n(8)d8/jc,f(x^8)n{6)d8.
EI siguiente ejemplo muestra un resultado de este tipo y, aunque muy sirnplista, ilustra un problema de incremento de incertidumbre a posteriori a pesar
de que aurnente nuestra información muestral.
E^emplo
Sea el espacio rnuestral X={x^ , x2 } y el espacio paramétrico O={61, 82 }.
Supongamos rc (9; )= 0.5, i= 1, 2, y sea la función de probabilidad fo (x ^ 9) la
dada por los valores de la tabla ^.
Tabla 1
VALORES DE fo (x ^ 8)
x2
8^
0.37
0.63
62
0.38
0.62
Supongamos que estamos interesados en A={91 } y que hemos observado x1.
Entonces nuestra inferencia para el modelo base fo resulta P^^ (81 ^ x^ )= 0.49,
0
y para la clase ^^^ con ^= 0.2 y S= 0.1 obtenemos
inf
fE ^j21
Pf (H1 ^ x1 )= 0.47,
sup
Pf (81 ^ x1 )= 0.52
fE '^.21
La robustez en .`^21 de nuestra inferencia vale, pues, R(H1 ^ x1 )= 0.05.
Para la observación muestral x=(x1, x1, x^ ), la probabilidad a posteriori
de H1 resulta Pf^ (8y ^ x1, x1, x1 ) = 0.48 y la robustez en la clase ^°1,
^f^y
E^"1'I!^^1A('IOti ROHl'ti^I:l
R(e, ^ x1, x^ , x^ ) = 0.16, Es decir, al aumentar la información rnuestral el rango
de la probabílidad a posteriori de e, aumenta de 0.05 a 0.16. Es claro que
R(82tx^)=0.05yqueR(82^x^,x^,x^)=0.16.
Es fácíl probar que cualquiera que sea ^(0; )> o, i= 1, 2, hay sucesiones x^n ^
para las que
lim
inf
Pf (61^x^^^)=0, i=1,2
n-,^ fE %j21
lim
n --^ ^
sup
fE `J2
Pf (E^1 ^ X^^ ^)= 1,
i^ 1, 2
Esta falta de robustez a posteriori se debe a la no identificalidad de 8 por ,^2' .
Es claro que este problema es más serio si G? es la clase de todas las medidas
de probabilidad.
Nos gustaría oír la opinión del profesor Zamar al respecto, la que de antemano agradecemos.
JOAQUIN MUÑOZ-GARCIA
Departamento de Estadística e Investigación Operativa
Universidad de Sevilla
Quisiera comenzar agradeciéndole al Director de la Revista la oportunidad
que me brinda de poder participar en el posible debate que surgirá de los comentarios de este artículo sobre estirnación robusta; en él se recopilan muchos
de los resultados obtenidos por H. R. Zamar sobre esta materia. Ello ya es motivo suficiente para felicitarnos por ia realización de este trabajo.
En 1971, Hampel propuso una definición formal del concepto de robustez
que respondía al concepto intuitivo de lo que los estadísticos entendían por estimador robusto y, aunque a la definición dada no cabe plantearle objeciones
desde un punto de vista formal, es conveniente advertir la dificultad que tiene
decidir a partir de ella si un estimador es robusto o no. Esto hace que las investigaciones en robustez se dirijan principalmente a cuantificar la misma, tendiendo a utílízar estimadores cuantitativamente robustos, construidos mediante métodos que minimicen el sesgo o/y la varianza asintótica.
Para estudiar la robustez se ha considerado en el artículo una familia de distribuciones definida en [2], la cual puede ser considerada simple para explicar
las observaciones muestrales, aunque no conviene olvidar que el estudio y la
t ti I^I>l^ ^ It
^ F.^I^,^^tic^l.^^
comprensión ^ie tales modelos son fundamentales para la explicación de modelos más complejos. N© obstante, como es un modeio que trata de explicar las
posibles observaciones out/iers, es necesario traer a colación la conjetura de
Anscombe (196Q) sobre la variabilidad propia del modelo poblacional inicial;
ésta Ilevaría posiblemente a perturbar la fracción de contaminacián del modelo.
Este es un aspecto que en las Ilamadas técnicas de acomodación (estimación
robusta} de outliers, según la clasificacián propuesta por Barnett y Lewis (1994},
no suele considerarse tanto desde un punto de vista teórico como práctic©.
AI introducir los distintos tipos de robustez habría sido oportuno, en un trabajo de este tipo, recoger la definición de punto de ruptura de un estimador y su
relacián con aquellas otras medidas que se introducen en torno a las distintas
ramas de la robustez, como indica el autor; asimismo, pienso que se deberia
haber empleado el térmíno «robustez global», como ya se indica en el trabajo
de nJlartin, Yohai y Zamar (1989).
En la estimacián robusta deben plantearse dos niveles de protección, la correspondiente al modelo pobfacional del que se ha extraído ia muestra, o más
simplernente de la muestra en sí, y la correspondiente a la técnica estadistica
que se aplicará a los datos; esta apreciación la hago desde la definición de observación outlier dada por Muñoz-^arcía, Moreno-Rebollo y Pascual-Acosta
(1990}: «Un outlier es una observacián que siendo atípica y/o errónea se desvía
rnarcadamente dei comportamiento general de los datos experimentales con
respecta al criterio por el que han de ser analizados.» Y ella me Ileva a hacerme
algunas consideraciones dentro del problema de la estimación robusta. Los das
niveles de protección pueden interaccionar o pueden enmascararse, pueden
perderse propiedades de optimalidad o de proteccián cuando los estimadores
obtenidos para un nivel son modificados para utilizarlos en el otro, etc. Cuestiones similares a éstas me planteo con los ^ñ11 estimadores, por el hecho de tener
una estimación robusta (la varianza o la matriz de covarianzas} dentro de un esti mador robusto, y a las que añado el análisis del posible efecto que pueden
presentar en los procesos de convergencia de estos estimadores robustos.
BIBLIO^GRAFIA
AtiscoMe^E, F. J. {1960}: «Rejection of outliers», Technometrics, vol. 2, 123-147.
BARNETT, V., y LEwis, T. {1994}: Outliers ín Statistical Data (3rd Edition), Ed.
John Wiley & Sons.
R. D.; YoHA^, V. J., y zAMAR , R. H. {1989}: «Min-max bias robust regression^>, The Annals of Statisties, val. 17, 1608-1630.
MARTaN ,
MUÑOZ- C`
..aARCÍA, LJ.; MORENO-REBOLLO, J. L., ^/ PASCUAL-ACOSTA, A. (1 99O}: «OUt-
liers: A formal approach», lnternational Statistical Review, vol. 58, 215-226.
E-:ti l 1ti1.^^('It)ti Et( )Eil !, E;>
MANUEL ANTONIO PRESEDO QUINDIMIL
Departamento de Estadística e Investigación Operativa
Universidad de Santiago de Compostela
Quisiera agradecer, en primer lugar, a Estadística Española el ofrecirniento
para partícipar en esta discusión. También quiero felicitar al profesor Zamar por
este artículo que, en mi opinión, trata con gran claridad un problema tan complejo y a la vez tan interesante como es el de la estimación robusta, campo en
el que el autor posee una dilatada experiencia, como prueba la cantidad de trabajos publicados en los últimos años.
En particular, quisiera destacar la cuidada introducción al problema de la estimación robusta, presentada a lo largo de las dos primeras secciones de este
artículo, que permite que cualquier lector no iniciado en este tema pueda adquirir una idea clara acerca de lo que se pretende con su estudio, así como de los
distintos enfoques que se han venido desarrollando a lo largo de los últimos
años para el tratamiento de este problema.
En lo que sigue me voy a limitar a exponer un aspecto de la estimación robusta que entiendo que debe ser tratado en esta discusión:
La idea de los modelos paramétricos corno aproximaciones de la realidad
justifica la búsqueda de estimadores que sean «estables» ante pequeñas desviaciones del modelo supuesto. Aunque no existe un único criterio de robustez,
la búsqueda de estimadores robustos trata de resolver un compromiso entre la
«estabilidad» y la eficiencia del estimador, lo cual introduce una notable complicac'rón en los métodos desarrollados que dificulta su aplicación en la práctica.
Dejando aparte el aspecto computacional de ios estimadores robustos (na
siempre fácil de resolver en la práctica), que sólo puede abordarse con !a ayUda
del soporte informático, para su cálculo (como puede observarse en los distintos
casos tratados en las secciones 3 y 4 de este artículo) es necesario especificar
ciertas funciones y constantes que son elegidas por el interesado. Así, para el
estimador de Huber, al que se refiere el autor en la sección 5 de este artículo, el
valor de la constante c determina la eficiencia y la robustez del M estimador resultante y deberá ser propuesta por el interesado jen Hampel (1986, p. 138)
puede verse una extensa tabla en la que se relacionan distintas rnedidas de robustez, incluida la sensibilidad máxima a«gross errors», y la eficiencia en el modelo normal del estimador de Huber para diferentes valores de la constante c].
Por lo anteriormente expuesto, sería deseable disponer de algún criterio objetivo (basado en la información muestral) para la elección de tales funciones y
constantes. Me gustaría que el autor pudiera formularnos alguna indicación sobre este aspecto que facilite la aplicación en la práctica de los métodos de estimación robusta.
E.^ t^ ^r^l^, r t(':^ t-^E^:ti^v(>1-:^^
^7^
Por mi parte, nada más. Espero que este breve comentario pueda contribuir
a completar esta discusión s©bre el tema tratado en este artículo def profesor
Zamar, al cual reiter© una vez más mi feficitación.
REFERENCIAS
HAMPE^, R. I'i.; RONCHETTI, E. M.; ROUSSEEUW, P. ^J., ^/ STAHEL, W. A. (1976}:
RO-
bust Statistics. The Approach Based on Inf/uence Functions, Wiley.
MANUEL DEL RIO
Departamenta de Estadistica e i. O.
Universidad Complutense, Madrid
í.
Introducción
Mis felicitaciones af profesor Zamar por esta interesante exposición. Con
certeza, su visión de especiaiista en el problema de estimación robusta en sesgo animará a 1os estudiosos y usuarios de las métodos de regresión a incorporar a sus planteamientos habituales las ideas y métodos expuestos, así eomo a
la consideración de métodos robustos, compensando el excesivo peso que se
suele dar al criterio de mínimos cuadrados. EI comentario intentará complementar, sin entrar en aspectos muy específicas o técnicos, algunos de los temas expuestos en el trabajo, planteando finalmente algunas cuestiones relativas a aspectos de diagn+óstico.
Como es sabido, existen dos planteamientos básicos al tratar la robustez
frente ai sesgo cuando las distribuciones pertenecen a un entorno de cantaminación: a) EI enfoque local, consistente en el estudio del sesgo causado por una
pequeña proporción ^ de contaminación; está ligado al concepto de curva de influencia, introducido por Hampel (1974), que proporciona una aproximación lineal váiida para el sesgo producido por una contaminación ^^ g. b) EI enfoque
g/obal, que atiende al sesgo causado tanto por valores pequeños como grandes
de ^. Dentro de él, una medida importante de la robustez (ligada al máximo sesgo asintótico} es el punto de ruptura
PR , in#roducido por Hampel (1971) y
^s^riti^f^c^ic^^rv Ko^^'^s^r;^
que permite controlar lo peor que puede ocurrir en entornos «grandes» . En Donoho y Huber (1983) puede encontrarse una defensa de la utilización de este
concepto (muestras finitas) que, por diferentes razones, no fue muy considerado
en los comienzos del estudio de los métodos robustos.
En los últimos a^ios se han presentado diversas propuestas de estimadores
con PR alto en modelos de posición y de regresión; algunas de ellas han contado con la intervención del profesor Zamar y han sido revisadas en su trabajo.
Aun a riesgo de reiterar alguna de las exposiciones, consideraremos inicialmente el desarrollo histárico de estos estimadores restringiéndonos al caso de modeios de regresión.
2.
Estimadores con punto de ruptura máximo
Comencemos recordando que tanto los M-estimadores de regresión como su
mejora mediante los GM-estimadores, diseñados para controlar el efecto de regresores con alto potencial, no resuelven satisfactoriamente la cuestión de! PR.
La razón básica reside en que éste decrece en modelos con gran número de regresores, justamente cuando existen más posibilidades de casos con alto potencial.
EI primer estimador con PR máximo ( 50%) es el estimadar de medianas repetidas, Siegel {1982). Puede ser calculado explícitamente, si bien su obtención
es costosa, pues precisa considerar todos los subconjuntos con p observaciones, siendo p el número de regresores. CJtro inconveniente reside en no ser
equivariante bajo transformac'rones lineales de los regresores.
Rousseeuw {1984} íntroduce el estímador consistente en minimizar la mediana
de los cuadrados de los residuos
least median of squares ( LMS) : med r,?.
Este estimador alcanza PR máximo y es equivariante; sin embargo, su eficiencia asintótica es baja debido a su lenta tasa de convergencia (n-'^3 }. Para solventar este inconveniente, Rousseeuw ( 1984) propone el estimador de mínima
suma truncada de cuadrados
least trimmed squares ( LTS) , consistente en
minimizar ^ ;'_ ^ r ^^ ; „? , donde r ^^ ; ,^ ^ < . . . ^ r ^^ : ^ ^ son los cuadrados ordenados
de los residuos. con PR máximo, su tasa de convergencia es la habitual ( n-'^2 ).
Sobre la elección óptima de h puede consultarse Rousseeuw y Leroy (1987, páginas 132-134}.
Notemos que la idea que subyace en la construcción de los dos últimos estimadores es «robustecer» la medida de error del criterio mínirno-cuadrático mediante una rnedida robusta de la dispersión de los residuos. Manteniendo este
planteamiento, Rousseeuw y Yohai (1984) consideran los S-estimadores de regresión, basados en minimizar un M-estimador de escaia para los residuos aso-
F^ F.^[)Iti F Ic':^^ F-:tiF',^^Jt ^l ,1
ciados al vector de regresión genérico ^3. Los S-estimadores pueden alcanzar un
PR máximo, si bien a costa de perder eficiencia, siendo su comportamiento
asintótico similar al de los M-estimadores de regresión.
Una completa exposición de Ias propiedades de estos tres tipos de estimadores puede verse en Rousseeuw y ^eroy ( 1987, pp. 112-145), donde se incluye asimismo una discusión sobre su relación con las técnicas denominadas projection pursuit.
Con el objetivo de conseguir eficiencia alta para estimadores con punto de
ruptura alto, Yohai (1987) propone los denominados MM-estimadores. Se definen en tres etapas, las d©s primeras buscan alcanzar un PR alto y la última obtener eficiencia. En primer lugar, se considera un estimador j3* con punto de
ruptura alto {p. ej., LMS o LTS); a continuación, utilizando los residuos de este
ajuste, se obtiene un estimador de escala 6^ con PR = 50%; finalmente, se define e! MM-estimador de los parámetros de regresión como cualquier solución
que minimice S(^i} _^ p{r; {^i} / 6„ } y sa#isfaga S(^3} < S( ^3*), siendo p función
del tipo utilizado en S-estimación. ^a última etapa permite alcanzar eficiencia
alta, pues la función p puede ser muy diferente de la usada para el estimador de
escaia c^„ de 1a segunda etapa. Esta idea de combinar PR alto con eficiencia alta
es también utilizada por Yohai y Zamar ( 1988) para definir 1os ^-estirnadores de
regresión expuestos en el trabajo.
Apuntemos que la definición de PR en regresión no lineal presenta dificultades relacionadas con su estabilidad frente a reparametrizaciones; en Stromberg
y Ruppert (1992) puede encontrarse una discusión de este problema junto con
una propuesta de solución.
En relación con el aspecto computacional, notemos que la mayoría de las algoritmos para calcular estimadores de regresión con PR afto se basan en realizar ajustes minimo-cuadráticos en un número elevado de subconjuntos de p
puntos {ver Rousseeuw y Leroy, 1987, cap. 5}. AI ser este planteamiento impracticable en regresión no lineal, Stromberg ( 1993) ha considerado un nuevo
algoritmo {de hecho, una modificación del conocido algoritmo PROGRESS) que
requiere un número de ajustes bajo. EI algori#mo se utiliza para calcular los estimadores LMS y MM, incluyéndose resultados de simulación que comparan el
comportamiento de ambos estimadores en tres modelos no lineales clásicos.
También se presentan ejemplos mostrando cómo estos estimadores son útiles
para detectar observaciones anómalas en el caso no lineal.
3.
Estimadores con sesgo minimax
Tanto la función de influencia camo el PR pueden ser insuficientes para
describir adecuadamente el sesgo de un estimador. Para conseguir protección
r.s-rrtit^^c^r^^?v kc,Hi ^^; r :^
frente a distribucior^es en un entorno, puede ser más adecuado trabajar directamente con el sesgo bajo contaminación y utilizar el máximo sesgo asintótico
para fracciones de contaminación inferiores al PR. Esto conduce a la búsqueda
de estimadores minimizando el máximo sesgo asintótico en un ^-entorno de
contaminación. Recordemos, como hace el profesor Zamar, que esta idea ya
fue considerada por Huber, si bien esta aproximación a la robustez global parece haber sido dejada de lado hasta hace unos años; varios resultados e ideas
interesantes en problemas de localización y regresión se exponen en su trabajo. Sin entrar en detalles, revísaremos brevemente algunos resultados recientes obtenidos bajo este planteamiento en modelos de regresión.
En Martin, Yohai y Zamar (1989} se presentan estimadores robustos con
sesgo minimax para dos clases diferentes de estimadores de regresión: i) Mestimadores basados en funcíones p acotadas y con estimador de escala general para los residuos (estos estimadores pueden ser considerados S-estimadores y tienen la misma tasa de convergencia que el estimador LMS); y ii) GM-estimadores con curva de influencia acotada. En particular, se rnuestra que para
la regresión simple a través del origen (p - 1), el GM-estimador minimax es la
mediana de las pendientes ( y; l x^ ), siendo este estimador también minimax en
la clase de los estimadores equivariantes por transformaciones lineales. EI trabajo incluye una comparación, para distintos valores de p, de los sesgos rninimax para los estimadores S, GM y LMS bajo el modelo normal multivariante.
En Zamar (1992) se consideran modelos de regresión con errares en !as variables. En este contexto, se analiza el comportamiento del máximo sesgo de
M-estimadores en entornos de ^-contaminación con distribución central Fo - N
(µ, E+ a2 /}, obteniéndose el correspondiente estimador óptimo. Indiquemos
que los M-estimadores en el contexto citado fueron previamente consíderados
por Zamar (1989).
Citemos, finalmente, el trabajo de Maronna y Yohai (1993), en donde se introduce y estudia un nuevo tipo de estimadores de regresión con robustez aita
respecto al sesgo (ver también Maronna y Yohai, 1991). Estos estimadores,
denominados por los autores P-estimadores, se construyen partiendo de un estimador robusto y equivariante por transformaciones iineales del parámetro de
regresión simple a través del origen. A continuación, se obtiene un óptirno al
considerar las regresiones simples de la respuesta frente a todas las proyecciones unidimensionales de los regresores. En particular, se prueba que utilizando como estimador inicial la mediana de las pendientes, el estimador resultante es robusto frente al sesgo, obteniéndose una cota superior para su máximo sesgo.
E:S"TAUIti ^'1('A }^,SF'Ati()LA
4.
Diagnóstico y regresión robusta
Las técnicas de diagnóstico, diseñadas para un estudio crítico de distintos
aspectos del modela, así como de la influencia de los casos en el análisis, tienen un gran interés en la valoración a posteriorr del ajuste de un modelo a un
determinado conjunto de datos. Una revisión condensada de la numerosa li#eratura sobre estas técnicas puede verse en Del Río (1990}. Huber {1991) analiza
la relación entre robustez y diagnóstico, así como sus papeles complementarios
en el análisis de regresión. Los dos volúmenes donde se pubiica el último trabajo citado cantienen interesantes aportaciones sobre diagnóstica en/y regresión
robusta.
En el árnbito del presente comentario, indiquemos que los estimadores con
alto PR, particularmente e! estimador LMS, han sido utilizados en distintos contextos para identificar observaciones anómalas y revelar problemas de especificación incorrecta o enmascaramiento que otras técnicas pueden no detectar
(ver, por ejemplo, Atkinson, 1986, 1988; Rousseeuw y Van Zomeren, 1990;
Cook, Hawkins y Weisberg, 1992).
Los residuos son una herramienta básica del diagnóstico y su utilización más
simple en ajustes mínimo-cuadráticos la constituyen los diversos gráficos de residuos propuestos. Una cuestión importante es analizar si Ios gráficos de residuos construidos a partir de un ajuste robusto tienen interpretaciones similares
a las de sus análogos mínimo-cuadráticos. En McKean, Sheather y Hettmansperger {1993} se presenta un interesante estudio de las propiedades de los residuos y valores ajustados bajo el modelo correcto y modelos alternativos para M
y GM-estimadores. Sus conclusiones básicas son las siguientes: la interpretación en el caso de M-estimación con funciones monótonas es similar al caso mínimo-cuadrático; la interpretación para ^M-estimadores no es tan directa debido
a que la matriz de diseño está involucrada en la aproximación de primer orden
que se utiliza en el trabajo; por otra parte, los resultados de simulación muestran poca capacidad de los residuos para detectar no aleatoriedad.
^os dos párrafos anteriores conducen de modo natural a ias siguientes cuestiones. Primeramente, ^son útiles como elemento de diagnóstico, en la línea del
estimador LMS, los estimadores revisados en el trabajo, como los M-estimadores de escala, los S y i-estimadores y los dos tipos de estimadores de Martin
et al. {1989)? Su igual o mejor comportamiento teórico hace suponer una respuesta esperanzadora. En segundo lugar, Lcómo obtener resultados sobre el
comportamiento de los residuos obtenidos tras ajustes que utilicen los últimos
tres tipos de estimadores citados? Finalmente, y recordando el trabajo de Stromberg (1993) comentado anteriormente, ^,cuál puede ser la utilidad de esos tres
estimadores para detectar observaciones anómalas en mod'eios de regresión lineal y no lineal?
#^S"I'IMAC'IC)N kO^3US'f^^A
REFERENCIAS ADICIONALES
ATKINSON ,
A. C. (1986): «Masking unmasked», Biometrika, 73, 533-541.
(1988): t<Transformations unmasked», Technometrics, 30, 311-318.
COOK, R. D.; HAWKINS, D. M., y WEISBERG, S .
(1992): «Comparison Of model
misspecification diagnostics using residuals from least median of squares
and least median of squares fits», J. Amer. Statist. Assoc., 87, 419-424.
DorvoHO, D. L., y HUBER, P. J. (1983): «The notion of breakdown point», en
A Festchrift for E. Lehman, P. Bickel, K. Doksum y J. L. Hodges (eds.),
Wadsworth, Belmont, CA.
HAMPEL, F. R. (1971): «A general qualitative definition of robustness», Ann.
Math. Stat., 42, 1887-1896.
HUBER, P. J. (199^ ): «Between robustness and diagnostics», en Directions in
Robust Statistics and Diagnostics, Part l, W. Stahel y S. Weisberg (eds.),
Springer-Verlag, New York.
MARONNA, R. A., y YOHAI, V. (1991): «Recent results on bias-robust regression
estimates», en Directions in Robust Statistics and Diagnostics, Part 1,
W. Stahel y S. Weisberg (eds.}, Springer-Veriag, New York.
-- (1993): «Bias-robust estimates of regression based on projections», Ann.
Statist., 21, 965-990.
MCI'CEAN, J.; SHEATHER, S., y HETTMANSPERGER, T
. (1993): «The use and interpre-
tation of residuals based on robust estimation», J. Amer. Statist. Assoc., 88,
1254-1263.
DEL Río, M. (1990}: ^CDiagnóstico en modelos de regresión», Rev. Real Acad.
Diencias Ex., Fís. y Nat., 84 ( 3), 521-524.
RoussEEUw, P. J., y YOHAI, V. (1984): «Robust regression by means of S-estimators», en Robust and Nonlinear Time Series Ana/ysis, J. Franke, W. Hardle y
R. D. Martin {eds.), Springer-Verlag, New York.
RoussEEUw, P. J., y VAN ZOMEREN, B. C. (1990): «Unmasking multivariate outliers and leverage points», J. Amer. Statist. Assoc., 85, 633-639.
SIEGEL, A. F. (1982): «Robust regression using repeated medians», Biometrika,
69, 242-244.
STROMBERG, A. J. {1993): «Computation of high breakdown nonlinear regression
parameters», J. Amer. Statist. Assoc., 88, 237-244.
STROMBERG ,
A. J., y RUPPERT, D. (1990): «Breakdown in nonlinear regression»,
J. Amer. Statist. Assoc., 87, 991-997.
ZAMAR, R. H. (1989): «Robust estimation in the errors in variable models», Biometrika, 76, 149-160.
;^x
^^.ti^l -^C)t!i^t i( ^ ^ E^:^f':^^ ^ ti't ^ [_ ^^
SANTIAGO VELILLA (*}
Departamento de Estadística y Econometria
Universidad Carlos III de Madrid
Agradezco, en primer lugar, a la Revista Estadístiea Españala por la oportunidad de participar en la discusión del trabajo invitado «Estimación Robusta» y,
por extensión, en un debate ampiio sobre las técnicas de estimación robustas.
EI articulo del profesor Zamar comienza con una motivación sobre la necesidad
de introducir técnicas robustas, el contexto en el que éstas se han de construir y
la discusión de varios criterios de robustez. La segunda parte del artícula revisa
varias propuestas de estimadores robustos en regresión (estimadores M, S y i,
y estimadores con influencia acotada), para terminar con una presentación de
resultados recientes sobre (a función de sesgo máximo y el cálculo de estimadores con sesgo minimax. Mis comentarios se refieren tanto al artículo como a
cuestiones que creo de interés en un debate general sobre estimación robusta,
y se dividen en tres apartados: 1) Motivación y aspectos generales; 2) Elección
del criterio de robustez; y 3) Aspectos numéricos.
Motivación y aspectos generales
Es una idea clásica en robustez argumentar la insuficiencia de un modelo
«central» paramétrico {,^H }^ E ^ para explicar un conjunto de datos X; , i= 1, ..., n,
y proponer como alternativa el modelo de contaminación de Tukey
^^_{F:F=(1-^)F^+€H,OEO}
[1]
donde 0< E<.05 es fijo y H es arbitraria y desconocida. EI artículo ilustra una
aplicación de [1 ] al caso de la media muestral X=^ X; / n, cuando se toma
i=1
como modelo central una N(µ, 6), H es N(µ + 6, a) y^_.05 (µ = 1, 6= .03}. Es
inmediato que las propiedades de eficiencia de X se deterioran sustancialmente
en el paso de fo ^ N(µ, cs) a(1 -^) fo +^ f^ , donde f^ ^ N(µ + 6, a), pese a que,
como argumenta Zarnar, las densidades fo ^ N(µ, a) y(1 -^) fo +^ f1 son prácticamente indistinguibles. Por ejemplo, la distancia del supremo entre fo y f^ es trivialmente menor que 2^ / 6(2^)'^2. Sin embargo, creo que debería insistirse en
que esta deficiencia es un mero reflejo de la falta de continuidad (en cierto sentido) de X respecto a una medida de la distancia entre las posibles densidades
generadoras de los datos. Pese a que j ^ fo - f1 ^^^, es pequeña, las densidades fo
y la mixtura (1 - c) fo +^ f^ producen, en general, conjuntos de datos muy diferen(*)
Trabajo financiado en parte por el proyecto PB93-0232 de la DGICYT.
f-:S"f Iti1At'1()!^ Kc)fil ti l;^
.^ 7 ^)
tes. Para ver esto, basta considerar el siguiente ejemplo. Sean {X; o, i= 1, ..., n}
datos de N(µ, 6) y sean {X; ^, i= 1, ..., n} datos de N(µ + 6, 6). Se definen
(
E;) X;o+^;X;^
[2]
donde los {E; } son variables que toman valores 0 y 1 con probabilidades 1-^ y
£, respectivamente, y tales que las ternas (^; , X; a,X; ,) son i.i.d., donde, además, ^; es independiente del par (X; o, X;1 ) . Es inmediato que los {X; } son una
muestra del modelo (1 - E) fo + c f1 . Para los casos ^_.05 y .10, µ= 1 y a=.03,
la tabla 1 recoge n= 30 datos simulados de fo ( Xo ), de f1 (X^ ) y de la mixtura
(1 - E) fo +^ f1 (XX^ , XX2 ) de acuerdo con la técnica [2]. Es inmediato que las
columnas Xo y (XX1 , XX2 ) difieren en la aparición de las observaciones anómalas 19 y(24, 27), respectivamente, que están rnuy alejados de la media µ= 1
del modelo central. Los datos hablan por sí solos de la necesidad de construir
un estimador T„ = T„ [X1 ,..., X„ ] para µ, alternativo a X y que sea menos sensible ante la aparición de datos anómalos.
Otro punto de interés relativo al entorno [1 ] es la interpretación del modelo
de perturbación, en particular de la distribución H responsable de las desviaciones dei modelo «central», y la interpretación de los resultados de un análisis robusto o, en otras palabras, dado el valor observado de un estimador robusto
T„ = t„ = T„ [x1 ,..., xn ], qué parámetros se están estimando. En el caso simple
en el que {^e }^ E ^ es un modeío de posición en ^^, un estimador robusto natural
es med ( X;), que resulta ser un estimador de la posición 9, libre del efecto de la
perturbación H. Cuando la dimensión de los datos aurnenta, la respuesta, en rni
opinión, no es tan sencilla. En un problema de regresión en el que los datos z;
presentan una estructura natural de la forma z; _ (y; , x; )' donde y; es una respuesta escalar y x; es un vector de regresores, el significado del estimador depende de varios factores; entre otros, la elección de: a) ia distribución marginal
Go (x ) de los regresores bajo el modelo central Fo (y , x); b) la distribución condicionada Ho (y ^ x) en el modelo Fo (y , x ), y c) los análogos G(x ) y H(y ^ x)
en la distribución de perturbación F(y , x). EI punto c) implica una caracterización de puntos anómalos tanto en el espacio de las variables {y; } como en el
espacio de los regresores {x; } que es siempre delicada, en particular en dimensión p >_ 3. Por ejemplo, la construcción de un M-estimador de regresión obtenido como solución de una ecuación de la forma
n
(1 /n).^,x; y^[(Y; -x; [3)/cs] =0
[3]
^=1
donde la función yr = p' y p(t )= t 2 / 2 (^ t ^
< c); p(t )= c ^ t ^(^ t ^> c), depende
críticamente de la elección de !a constante c> 0 que, irnplícitamente, caracteriza el urnbral a partir del cual los residuos r; (^i) = y; - x; R se consideran gran-
des en magnitud y su intervención en la ecuación de estimación [3] se toma
ES)Al)Iti"II('.A ESPAtiO1.,^1
T^bl^ 1
MUESTRAS SIMULADAS DE TAMAÑO n= 30 DE LAS DENSIDADES
fo (Xo ), f^ (X^ } Y (1 - ^) fo + F f^ , DONDE fo ^- N (1, .03), f^ ^ N (7, .03}
Y^=.05(XX^)Y.10(XX2)
i
Xo
x,
1
1.0213
2
.9441
3
.9776
6.9824
7.0123
6.9799
4
5
.9588
.9627
6
^ . oso4
7
8
9
10
1.0013
1.0330
1.0352
1.0357
11
1.015$
12
1.0341
13
14
.9788
1.0463
15
1.0481
16
17
18
.9826
.9889
.9810
19
.9737
20
21
22
23
24
25
26
.9566
.9551
1.0035
1.0076
.9700
1.0179
.9949
27
.9875
28
29
30
1.0126
.96E6
.9987
7.0448
7.01 1 E
7.0590
7.0066
7.0324
7.0289
7.0087
7.031 1
6.9246
7.0359
6.9887
7.0156
7.0405
6.9660
7.071 1
6.9905
7.0163
6.991 1
6.9845
7.0030
7.0194
6.9439
6.9806
6.9996
6.9931
6.9857
6.9801
.0
.0
.0
.0
.0
.0
.0
.a
E2
X^C1
xx2
.0
.0
.0
.0
1.0213
1.0213
.9441
.9776
.9588
.9441
.9776
.9588
.o
.o
.o
.o
.o
.9627
.9627
1. 0604
1.0013
1.0330
1. a352
.0
.0
1.0357
1.0158
1.0604
1 .0013
1 .0330
1 .0352
1 .0357
1 .0158
.0
.0
.0
.0
.0
.o
1.0341
1.0341
.0
.a
.o
.9788
1.0463
.9788
1 .0463
.0
.0
1. 0481
1 .0481
.o
.o
.0
.0
1.0
.0
.0
.0
.0
.0
.0
.0
.0
.0
.0
.0
.0
.0
.0
.0
.0
.0
.0
1.0
.0
.0
1.0
.0
.0
.9826
.9889
.9826
.9889
.9810
.9810
6.9905
.9566
.9551
1.0035
1.0076
.9700
1.0179
.9949
.9875
.9949
6.9996
1.o12s
1.0126
.9626
.9987
.9626
.9987
.9737
.9566
.9551
1.0035
1 .0076
7.0194
1.0179
constante e igual c. Una elección incorrecta de c puede ir en serio detrimento de
^
las propiedades de robustez e interpretabilidad del M-estimador [in obtenido al
solucionar [3].
FSTIti1AClON RUBI_-STA
2.
Elección del criterio de robustez
EI artículo del profesor Zamar se concentra en recientes trabajos sobre la
construcción de estimadores con sesgo minimax. Minimi2ar el sesgo asintótico
es una forma de paliar el efecto de la perturbación en la estimación, dado que el
sesgo asintótico se define como
IIT[F]-eIIM
[4]
donde M es una matriz definida positiva, elegida usando argumentos de invarianza, T[F ] es el funcional asociado a la definición del estimador T„ [X^ ,...,
X„ ]= T[F„ ] como función de la distribución empírica de los datos y ^ ^ a ^ ^M =
_{a' Ma )'^2 es la norma elíptica asociada a M. Se observa que [4] involucra explícitamente que la convergencia de T[F,^ ] es hacia T[F ] que, para F general
en el entorno [1 ], será diferente de 9 0, en otra ^ palabras, que los estimadores
T[F^ ] son inconsistentes para e pese a imponer la restricción de consistencia
Fisher T [Fe ]= 8 en el modelo central. La curva de sesgo asintótico máximo
B{T, ^) =
suP
F E ^^.
II T[F] - 9 IiM
[5]
se relaciona también de forma inmediata con el punto de ruptura de T[F ][Martin, Yohai y Zamar ( 1989)]. La teoría basada en la minimización de [5] conduce
a resultados interesantes, pero creo que debería complementarse con algún resultado de convergencia asintótica del tipo n 12 [T^ - 8] ^ Np [o, ^], donde p es
la dimensión del parárnetro e, que permitiera estudiar y comparar las eficiencias,
bajo el modelo central {^^ } e E o, de T^ con el estimador de máxima verosimilitud. Este parece ser el contexto de recientes investigaciones [Coakley y Hettmansperger ( 1993); Croux, Rousseeuw y Hóssjer ( 1993)] en la búsqueda de estimadores de regresión eficientes y de punto de ruptura próximo a 1/2.
Aspectos numéricos
Esta es una cuestión fundamental, puesto que la determinación de los estimadores robustos depende siempre de técnicas computacionales más o menos
sofisticadas y, en ocasiones, de la minirnización de funciones no convexas con
mínimos locales. La complejidad del problema aumenta en dimensiones altas
(tanto en el número n de datos corno en la dimensión p del parámetro), como
ilustra un reciente trabajo de Woodruff y Rocke (1994). La elaboración de algoritmos manejables, que implementen en la práctica la computación explícita de
los diferentes tipos de estimadores propuestos, facilitaría la comprensión y asimilación de las técnicas robustas por una audiencia mayor de estadísticos.
E,ti l.t[)1^ I I('t> F-tiF'Ati()1.,1
REFEREI^ICIAS ADICIONALES EN LA DISCUSION
. (1993): <^A Bounded Influence, High Breakdown, Efficient Regression Estimator», JASA, 88, 872-880.
COAKLEY, C., y HETTMANSPERGER, T
CROUx, C.; RoussEEUw, P., y Hc^ss^ER, O. (1993): «Generalized S-Estimatars>^,
Report No. 93-a3, revised version, Dept. o# Mathematics & Computer Science,
University of Antwerp, Bélgica.
WOODRUFF, D. L., y RocKE, D. M. (1994}: «Computable Rabust Estimatian of
Multivariate Location and Shape in High Dimension Using Compound Estimators>^, JASA, 89, 888-89fi.
VICTOR J. YOHAI
Universidad de San Andrés y Universidad de Buenos Aires
Quisiera felicitar a Rubén Zamar por su excelente exposición sobre los métodos estadísticos robustos para los modelos de posición y regresión.
En mi comentario me referiré a otro enfoque para obtener estimadores con
buenas propiedades de robustez para problemas de regresión múltiple: las estimadores basados en proyecciones.
Sea z; _ ( y; , x; ), 1^ i<_ n, y E I^ , x; E I^.p una muestra correspondiente a un
modelo de regresión lineal; por lo tanto, se tiene
+ u;
[1]
Antes de definir el estimador basado en proyecciones, consideraremos las
transformaciones que dejan invariante el problema de regresión. Apliquemos la
siguiente transformación a!os elementos de la muestra
= a y; + y' x; ,
z;*=(Y;*^x;*)^
^ ^i
donde A es una matriz de p x p no singular, y ^ I^^P y a E I^ . Luego es inmediato
que las z;* también satisfacen el modelo de regresión [1 ] con parámetro
8= A-1' {a 8 + ^y} y u;* = a u; . Por io tanto, resulta natural exigir que un estimador
^
6 satisfaga la siguiente propiedad
ESTIMAC'1ON ROBC'5^^1^^A
9(Z^*, ,..,Z„)=A-''(a6(z^, ...,2„)+Y)
[2]
Un estimador que satisface [2] se denomina equivariante.
Martin, Yohai y Zamar (1989) encontraron el estimador minimax en la ciase
de estimadores GM definidos por la ecuación [17]. Este corresponde a la función
^(r,x)=signo(r)x.
Para el modelo de regresión univariada que pasa por el origen, es decir, cuando
p= 1, el estimador minímax GM puede expresarse como
Y;
, 1 <_ i <_ n
x;
mediana
[3]
Maronna y Yohai (1993) prueban que este estimador también es minimax en
la clase de todos los estimadores equivariantes. Vamos a generalizar este estimador para p > 1.
EI estimadvr dado por [3] también se puede definir por
^
r; (e)
mediana
x;
, 1 <_ i <_ n
Una forrna de generalizar esta ecuación sería definir un estimador por
^
r; {e)
mediana
^, x, 1<_ i<_ n= 0
^
d^, E I^p
[4]
n
Esta ecuación está expresando que se busca un valor 6 de tal manera que
los residuos r; (9) no tengan ninguna estructura de regresión con ninguna combinación lineal ^.' x, y por lo tanto que, al aplicar el estimador ^de regresión dado
por [3], tomando como variable dependiente los residuos r; (9) y como variable
independiente las proyecciones ^' x; , éste da el valor cero.
Sin embargo, como en general^[4] no tendrá solución, se definirá el estimador de proyección por aquel valor 9 para el cual esta ecuación esté «más próxima» a ser satisfecha. EI significado exacto de la expresión «más próxima» se
precisará a continuación. Para esto definimos
n
A (^) = sup s (^,)
Á, E ]E8 ^
mediana
r; (e)
^,' x;
, 1 <i<_n
[5]
t-.S I Al)Iti"1 1{',3 ^-^51'r^Nt)L:^
donde s(^) es un estimador de la escala de las proyecciones ^.' x; y que puede
estar dado por
s (^.) = mediana {^ ^,' x, ^, ..., ^ ^,' x„ j^
EI propósito de utilizar esta escala en [5j es hacer que el estimador resulte equivari ante .
^
La ecuación [4j puede ser escrita como A(8) = 0. Como, en general, esto no
es posible, Maronna y Yohai {1993) definen el estimador de proyección {estimador P) por
argmin ^ ^ ^R A (8)
^
Se puede demostrar que si 6 es el estimador P, entonces para todo otro esti^*
mador equivariante 6 se tiene que
8 ^ {£} < 2 B ^- (E} + o (^)
donde o(^) /^---^ 0, y por lo tanto
B' ^ io) <- 2^' é' ío)
EI punto de ruptura del estimador P es o.5. Su orden de consistencia es n'^2,
pero la distribución asintótica no es normal.
Maronna y Yohai (1993} dan un algoritmo para computar el estimador de
proyección basado en submuestreo, similar al utilizado por Rousseeuw y Leroy
{1987) para estirnadores S, aunque de mayor compiejidad computacional. Si t
es el tiempo necesario para computar un estimador S, entonces el tiempo para
computar el estimador P es aproximadamente t log (t}.
Finalmente, compararemos los sesgos máximos y ia sensibilidad a errores
groseros para distintos estimadores. En 1a tabla 1, sacada de Simpson y Yohai
(1993), están los sesgos máximos del estimador minimax GM. En la tabla 2 están los sesgos del LMS y del estimador minimax S, que fueron obtenidos de
Martin, Yohai y Zamar (1989); y también los sesgos máximos del estimador P,
obtenidos de Maronna y Yohai {1993).
Observarnos que los P estimadores se comparan favorablemente respecto
del LMS y del estimador minimax S para todo p. También resulta que el estimador P tiene menor sesgo que el minirnax GM para p? 4.
Usando ideas similares a las desarrolladas aqui, Maronna, Yohai y Stahel
(1992) definen estimadares de proyección equivariantes para matrices de covarianza.
F^^^r^^^^c^^^^^v K^^^^^^-^^.^
Tabla 1
MAXIMtJS SESGOS DEL ESTIMADOR GM MINIMAX
p
y
F=.05
F=.10
E=.15
e=.20
1
2
1.57
2.00
0.08
0.10
0.18
0.27
0.28
0.47
0.41
0.83
3
4
5
10
15
2.35
2.67
2.94
4.06
4.94
0.15
0.17
0.18
0.27
0.33
0.34
0.43
0.49
0.83
1.30
0.67
0.92
1.29
^
^
1.72
^
^
^
^
20
5.66
0.41
2.31
^
^
Tabla 2
MAXIMOS SESGOS DE ESTIMADORES S Y P
Todo p
y
E=.05
^=.10
^=.15
^=.20
Minimax
^
0.49
0.77
1.05
1.37
LMS
^
0.53
0.83
1.07
1.52
3.14
0.16
0.36
0.56
0.82
P
REFERENCiAS
(1992): «BiaS-robust estimators of
multivariate scatter based on projections», Journal af Multivariate Ana/ysis,
MARONNA, R. A.; STAHEL, W. A`, y YOHAI, V. J .
42, 141-161.
MARONNA, R. A., y YoHAi, V. J. (1993): «Bias-robust estimates of regression based on projections», Annals of Statistics, 21, 965-990.
MARTIN, R. D.; YOHAi, V. J., y ZAMAR, R. H. (1989): «Min-max bias robust regression», The Anna/s of Statistics, 17, 1608-1630.
RoussEEUw, P. J., y LEROY, A. M. (1987}: Robust regression and outlier detection, Wiley, New York.
SIMPSON, D. G., y YoHAi, V. J. (1993): «Functional stability of one-step GM-estimators in linear regression», Technical Report #71, Department of Statistics,
University of Illinois Urbana-Champaign.
.^?^fl
F;^T Aí)I^ C`FC A E.SPAtii.)t_A
CO NT ESTA C I O N
En primer lugar, quiero agradecer al profesor Daniel Peña y a la Revista Estadística Española por esta oportunidad de discutir uno de mis temas favoritos:
estadística robusta. También quiero agradecer a los distinguidos comentaristas
por prestigiar rni contribucián con sus comentarios y sugerencias.
Mi trabajo no es una revisión de la teoría de robustez, sino una introducción
a ia misma. Consecuentemente, muchas cantribuciones importantes han sido
intencionaimente omitidas con el objetivo de simplificar la exposición y resaltar
las ideas centrales. Algunas de esas omisiones fueron recogidas por los comentaristas en sus comentarios. EI profesor Victor J. Yohai describe una clase rnuy
interesante de estimadores Ilarnados estimadores de proyección, el profesor Ricardo Maronna resalta la importancia e interés de ciertos problemas multivariados, el profesor Manuel del Río discute posibles aplicaciones de los métodos robustos en problernas de detección de outliers, y los profesores Elías Moreno,
Juan Antonio Cano y Julián de la Horra enfatizan las posibles conecciones con
el área de robustez bayesiana. La teoria de robustez presentada en mi articulo
está basada en el concepto de sesgo asintótico máximo y, por lo tanto, es de
naturaieza global. EI resuitado del ejemplo presentado por los profesores Moreno y Cano puede deberse a la alta proporción de autliers en la muestra. Si las
probabilidades condicionales de x^ y x2 son apraximadamente iguales {bajo los
dos escenarios posibles), entonces muestras muy desequilibradas, como por
ejemplo x1 , x1 , x1 , ..., x1 , serán muy atípicas y el consecuente colapso de la inferencia basada en tales rnuestras no sería entonces sorprendente.
Otros comentaristas resaltan ciertos problemas que aún subsisten y constituyen, en mi opinión, interesantes desafíos. Los profesores Alfonso García Pérez
y Santiago Velilla critican la naturaleza eminentemente asintótica de la teoría de
robustez. Puesto que una teoría basada en muestras finitas no será factible en
el futuro previsible, creo que se deberia prestar mayor atención al grado de uniformidad y a la velocidad de la convergencia de los estimadores robustos hacia
sus respectivos funcionales asintóticos. Martin y Zamar {1993) es un modesto
^-;5"1"INIA('I()N R()KIJS 1 :1,
paso en esa dirección. Los profesores Joaquín Muñoz García, Quindimif y Antonio Cuevas mencionan los problemas computacionales y la conveniencia de incluir métodos robustos en paquetes estadísticos comerciales. Yo concuerdo plenamente con ellos.
EI interesante comentario del profesor Alfonso Gordaliza sitúa mi trabajo en
un contexto m^s amplio dentro de la teoría de robustez y pone de relieve algunos aspectos que encontré muy interesantes.