integrales inmediatas

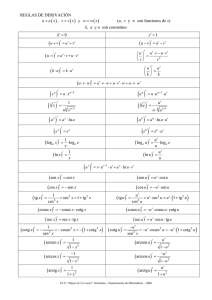
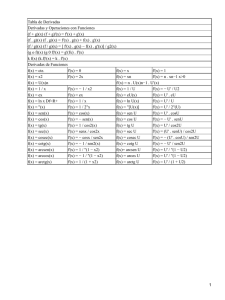
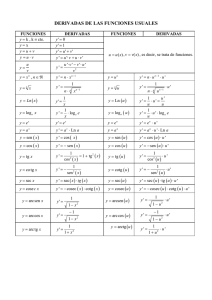
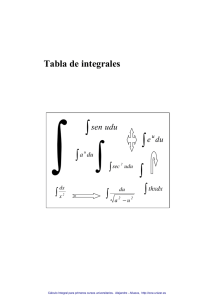
INTEGRALES INMEDIATAS
x n +1
+k
n +1
n
dx
∫x=
1
dx
∫=
x
∫e
x
( n ≠ −1)
dx
∫ cos x=
dx
∫ cos2 x =
2
⋅ u ′ ( x ) dx =+
e() k
u x
a()
⋅ u ′ ( x ) dx = + k
ln a
u x
− cos u ( x ) + k
∫ sen u ( x ) ⋅ u ′ ( x ) dx =
∫ cos u ( x ) ⋅ u ′ ( x ) dx =tg u ( x ) + k
∫ sec u ( x ) ⋅ u ′ ( x ) dx =tg u ( x ) + k
x=
dx tg x + k
x
− cotg x + k
∫ cosec x dx =
2
− cotg x + k
∫ (1 + cotg x ) dx =
2
1
2
2
∫ (1 + tg u ( x ) ) ⋅ u ′ ( x ) dx =tg u ( x ) + k
2
1
− cotg u ( x ) + k
∫ sen u ( x ) ⋅ u ′ ( x ) dx =
− cotg u ( x ) + k
∫ cosec u ( x ) ⋅ u ′ ( x ) dx =
2
2
− cotg u ( x ) + k
∫ (1 + cotg u ( x ) ) ⋅ u ′ ( x ) dx =
2
u′ ( x )
dx
∫ 1 + u=
2
( x )
1
dx arctg x + k
∫ 1+ =
x2
∫
ln | u ( x) | + k
tg x + k
dx =
− cotg x + k
2
u( x)
n +1
∫ cos u ( x ) ⋅ u ′ ( x ) dx = sen u ( x ) + k
2
1
∫a
u( x)
[u ( x)]n +1 + k
sen x + k
tg x k
∫ (1 + tg x ) dx =+
∫ sen
∫e
ax
+k
ln a
− cos x + k
∫ sen x dx =
∫ sec
u ′( x)
⋅ dx
∫ u ( x)=
ln | x | + k
dx= e x + k
x
dx
∫a=
1
n
∫ [u ( x)] ⋅ u ′( x) dx =
1
dx arcsen x + k
=
1 − x2

∫
arctg u ( x ) + k

u′ ( x )
=
dx arcsen u ( x ) + k
2
1 − u ( x ) 
I.E.S. “Miguel de Cervantes” (Granada) – Departamento de Matemáticas – GBG