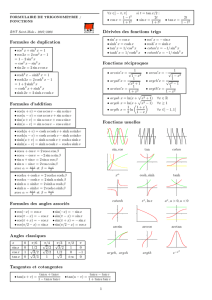
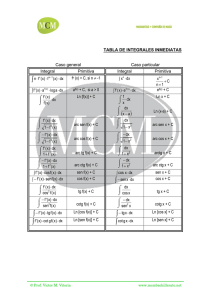
Document
Anuncio
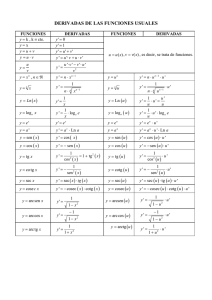
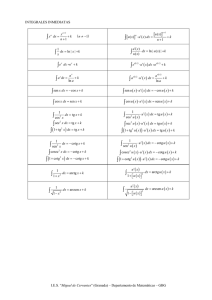
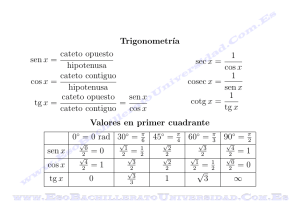
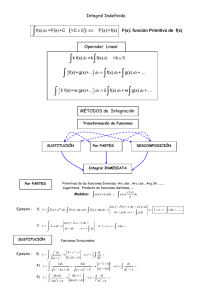
Tabla de integrales ∫ dx ∫x 2 ∫ sen udu ∫ a u du ∫ ∫ ∫ sec b ⌠ ⌡ 2 udu dudx f(x) ∫aa 2 −u2 u e du ∫ ∫ thxdx Cálculo Integral para primeros cursos universitarios. Alejandre - Allueva, http://ocw.unizar.es TABLA DE INTEGRALES 1) ∫ dx [ f ( x )] dx = f(x) + C 2) ∫ [ f (x ) ± g (x )] dx = ∫ f ( x ) dx ± ∫ g ( x ) dx 3) ∫ k f ( x ) dx = k ∫ f ( x ) dx d f ′( x ) f (x ) m dx = [ f ( x )] m+1 4) ∫ 5) ∫ f ( x ) dx = Log f ( x ) f ′( x ) f ′( x ) a f (x )dx = m +1 k = cte. +C +C a f (x) +C Loga 6) ∫ 7) ∫ f ′( x ) e 8) ∫ f ′( x ) sen [ f (x )] dx = − cos[ f ( x )] + C 9) ∫ f ′( x ) cos[ f (x )] dx = sen [ f ( x )] + C f (x) m =/ −1 dx = e f (x ) + C Cálculo Integral para primeros cursos universitarios. Alejandre - Allueva, http://ocw.unizar.es Tabla de integrales 227 10) ∫ f ′( x ) tg [ f (x )] dx = − Log cos [ f ( x )] +C 11) ∫ f ′( x ) cotg[ f (x )] dx = Log sen [ f ( x )] +C 12) ∫ f ′( x ) sec[ f ( x )] dx = Log sec [ f ( x )] + tg[ f ( x )] 13) ∫ f ′( x ) cosec[ f ( x )] dx = Log cosec[ f ( x )] − cotg [ f ( x )] 14) ∫ f ′( x ) sec [ f ( x )] dx = tg[ f ( x )] + C 15) ∫ f ′( x ) cosec [ f ( x )] dx = − cotg [ f ( x )] + C 16) ∫ f ′( x ) sec [ f ( x )] tg [ f (x )] dx = sec[ f (x )] + C 17) ∫ f ′( x ) cosec[ f ( x )] cotg[ f ( x )] dx = − cosec[ f (x )] + C 18) ∫ +C +C 2 2 f ′( x ) a 2 − [ f (x )] 2 f (x) dx = arcsen +C a Cálculo Integral para primeros cursos universitarios. Alejandre - Allueva, http://ocw.unizar.es 228 Introducción al cálculo integral − f ′( x ) 19) ∫ 20) ∫ a + [ f ( x )] a 2 − [ f (x )]2 f ′( x ) 2 2 f ′( x ) f (x) dx = arccos +C a 1 f (x) dx = arctg +C a a [ f ( x )] 1− n 21) ∫ [ f ( x )] 22) ∫ 1 − [ f ( x )] 23) ∫ [ f ( x )] 24) ∫ [ f ( x )] 25) ∫ f ′( x ) sh [ f (x )] dx = ch[ f ( x )] + C 26) ∫ f ′( x ) ch [ f ( x )] dx = sh [ f ( x )] + C 27) ∫ f ′( x ) th [ f (x )] dx = Log ch[ f (x )] + C dx = n f ′( x ) 2 +1 f ′( x ) 2 −1 n ≠1 +C dx = argth [ f ( x )] + C = f ′( x ) 2 1− n 1 | 1+ x | Log +C 2 | 1− x | dx = argsh [ f ( x )] + C= Log x + x 2 + 1 + C dx = argch [ f ( x )] + C = Log x + x 2 − 1 + C Cálculo Integral para primeros cursos universitarios. Alejandre - Allueva, http://ocw.unizar.es Tabla de integrales 229 f ′( x ) 28) ∫ ch [ f ( x )] dx = th [ f ( x )] + C 29) ∫ f ′( x ) sech[ f ( x )] dx = 2arctg e 30) ∫ f ′( x ) cosech[ f (x )] dx = Log th [ f ( x ) 2] 31) ∫ f ′( x )argsh 32) ∫ f ′( x )argch 33) ∫ f ′( x )argth 2 f (x ) +C +C f ( x ) dx = f (x )argsh f ( x ) − a a [ f ( x )]2 + a 2 +C f ( x ) dx = f (x )argch f (x ) ± [ f ( x )]2 − a 2 + C a a f (x) f (x ) − si argch > 0; + si argch < 0 a a f (x ) dx = f (x )argth f (x ) + a a a + Log f 2 ( x ) − a 2 + C 2 Cálculo Integral para primeros cursos universitarios. Alejandre - Allueva, http://ocw.unizar.es