u - Orange

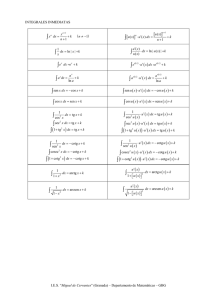
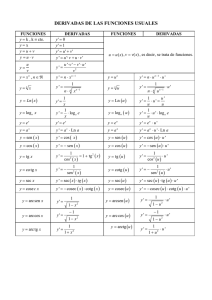
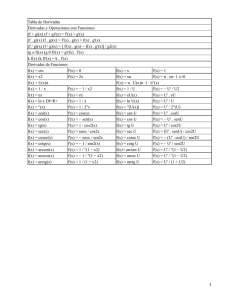
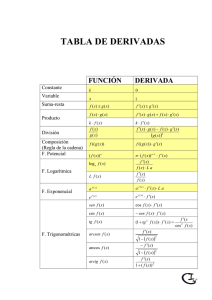
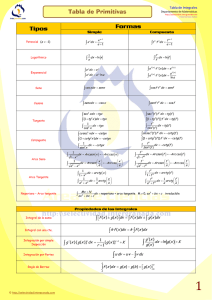
REGLAS DE DERIVACIÓN
u = u ( x) , v = v ( x) y w = w( x)
(u, v y w son funciones de x)
k, a y n son constantes
k′ = 0
x′ = 1
( u + v )′ = u′ + v′
( u − v )′ = u′ − v′
( u ⋅ v )′ = u′ ⋅ v + u ⋅ v′
⎛ u ⎞′ u ′ ⋅ v − u ⋅ v′
⎜ ⎟ =
v2
⎝v⎠
( k ⋅ u )′ = k ⋅ u′
⎛ u ⎞′ u ′
⎜ ⎟ =
⎝k⎠ k
( u ⋅ v ⋅ w )′ = u′ ⋅ v ⋅ w + u ⋅ v′ ⋅ w + u ⋅ v ⋅ w′
( x )′ = n ⋅ x
n
( x )′ = n
x
n
n
x
x
x
n
( a )′ = a
u
u
n −1
⋅ ln a ⋅ u ′
( e )′ = e
x
u
u
⋅u ′
u′
⋅ log a e
u
u′
( ln u )′ =
u
( log a x )′ =
( log a u )′ =
1
⋅ log a e
x
1
( ln x )′ =
x
(u )′ = v ⋅ u
v
( tg x )′ =
⋅ u′
n
n −1
⋅ ln a
( e )′ = e
n −1
( u )′ = n ⋅ uu′
1
n
( a )′ = a
(u )′ = n ⋅ u
n −1
v −1
⋅ u ′ + u v ⋅ ln u ⋅ v′
( sen x )′ = cos x
( sen u )′ = u′ ⋅ cos u
( cos x )′ = − sen x
( cos u )′ = −u′ ⋅ sen u
( tg u )′ =
1
= sec 2 x = 1 + tg 2 x
2
cos x
u′
= u′ ⋅ sec2 u = u′ ⋅ 1 + tg 2 u
2
cos u
(
( cosec x )′ = − cosec x ⋅ cotg x
( cosec u )′ = −u′ ⋅ cosec u ⋅ cotg u
( sec x )′ = sec x ⋅ tg x
( sec u )′ = u′ ⋅ sec u ⋅ tg u
( cotg x )′ = −
(
1
= − cosec 2 x = − 1 + cotg 2 x
2
sen x
1
( arcsen x )′ =
1 − x2
( arccos x )′ =
( arctg x )′ =
−1
1 − x2
1
1 + x2
)
( cotg u )′ =
)
−u ′
= −u′ ⋅ cosec 2 u = −u′ ⋅ 1 + cotg 2 u
2
sen x
u′
( arcsen u )′ =
1− u2
(
( arccos u )′ =
( arctg u )′ =
I.E.S. “Miguel de Cervantes” (Granada) – Departamento de Matemáticas – GBG
−u′
1− u2
u′
1+ u2
)