UNIDAD I. EL SISTEMA DE LOS NUMEROS REALES En
Anuncio
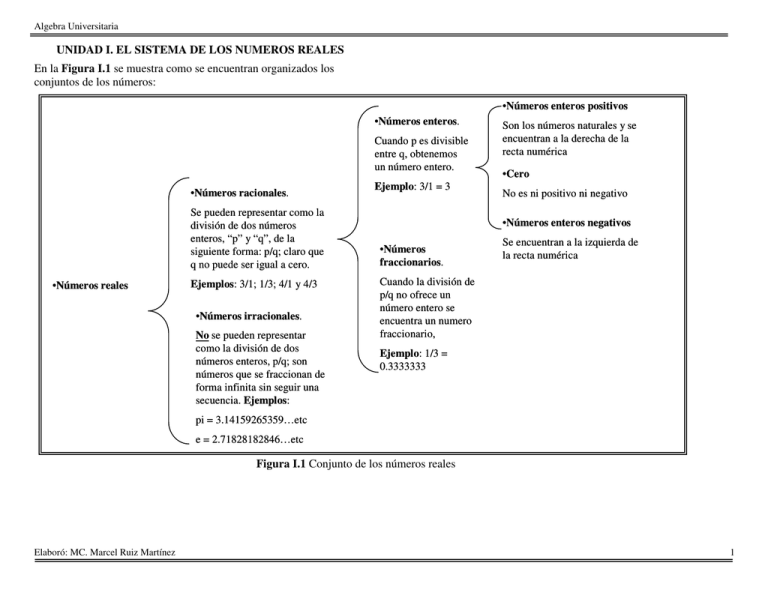
Algebra Universitaria UNIDAD I. EL SISTEMA DE LOS NUMEROS REALES En la Figura I.1 se muestra como se encuentran organizados los conjuntos de los números: •Números enteros positivos •Números enteros. Cuando p es divisible entre q, obtenemos un número entero. •Números racionales. Se pueden representar como la división de dos números enteros, “p” y “q”, de la siguiente forma: p/q; claro que q no puede ser igual a cero. •Números reales Ejemplos: 3/1; 1/3; 4/1 y 4/3 •Números irracionales. No se pueden representar como la división de dos números enteros, p/q; son números que se fraccionan de forma infinita sin seguir una secuencia. Ejemplos: Ejemplo: 3/1 = 3 Son los números naturales y se encuentran a la derecha de la recta numérica •Cero No es ni positivo ni negativo •Números enteros negativos •Números fraccionarios. Se encuentran a la izquierda de la recta numérica Cuando la división de p/q no ofrece un número entero se encuentra un numero fraccionario, Ejemplo: 1/3 = 0.3333333 pi = 3.14159265359…etc e = 2.71828182846…etc Figura I.1 Conjunto de los números reales Elaboró: MC. Marcel Ruiz Martínez 1 Algebra Universitaria 1.3.Conjunto de los números racionales Algoritmo de división en los enteros (y decimales) Los números racionales se le denomina a todo número que puede representarse como el cociente (o razón) de dos enteros con denominador distinto de cero (una fracción común). Realice la división de los siguientes enteros: 300 entre 15. Si dispone de esta hoja impresa,, puede hacerlo en este espacio en blanco: Definición a partir de los números enteros Consideremos a las parejas de números p, q; donde q es diferente de p cero. Los resultados de la razón se le conocen como números q racionales. Al conjunto de dichos números se les denomina Q y en lenguaje de conjuntos se denota de la siguiente manera: p Q = p ∈ Z , q ∈ Z , q ≠ 0 q Propiedades de la adición, multiplicación y orden de los racionales Son idénticas a las expuestas para los enteros. Expresión decimal de un número racional. Al realizar la división de p entre q, se pueden obtener expresiones decimales que caen dentro de estos tres tipos: Exacta.. Cuando la expresión decimal tiene un número finito de cifras. Por ejemplo: 5/2 = 2.5 Periódica pura: La parte decimal se repite de forma indefinida. Por ejemplo: 1/7 = 0.142857142857142857142857 1/3 = 0.333333333333333333333333333333 También puede expresarse: 1 1 3 = 0.3 7 = 0.142857 Periódica mixta: No toda la parte decimal se repite, por ejemplo: 1/60 = 0.01666666666666666666666 1 60 = 0.016 Elaboró: MC. Marcel Ruiz Martínez Video sugerido: http://www.youtube.com/watch?v=gX6ahfy http://www.youtube.com/watch?v=gX6ahfy-oNQ Densidad de los números racionales y representación en la recta numérica. Los números racionales cumplen la propiedad arquimediana o de densidad, esto es, para cualquier pareja de números racionales existe otro número racional situado entre ellos, propiedad que no estaba presentee en los números enteros, por lo que los números racionales son densos en la recta de los números reales. Para la representación ón de los racionales en la recta numérica érica te dejo los siguientes apuntes: apunt http://www.cidse.itcr.ac.cr/revistamate/AportesPe/Teoria/Racionales/Mod2/index.html También puedes uedes practicar con el siguiente software: http://www.cidse.itcr.ac.cr/revistamate/AportesPe/Teoria/Racionales/Mod2/applets/RecNum/RecNum.htm 2