INSTITUTO TECNOLOGICO SUPERIOR DE CAJEME CALCULO DIFERENCIAL

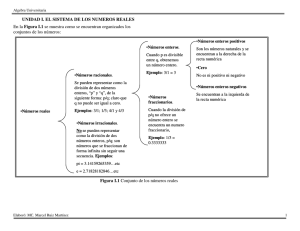
INSTITUTO TECNOLOGICO SUPERIOR DE CAJEME
CALCULO DIFERENCIAL
Unidad I. Los Números Reales
Hoy en día la ciencia y la tecnología han alcanzado niveles extraordinarios. El desarrollo de la física la
química, la biología, la astronomía, la medicina y la ingeniería y muchas ramas más fundamentan su
progreso en la aplicación de una de las herramientas más poderosas de las matemáticas: el cálculo
infinitesimal.
El desarrollo del cálculo se produjo al tratar de resolver problemas de la vida real, entre los más
conocidos podemos mencionar:
Describir la velocidad que lleva una partícula con velocidad constante.
Determinar la ecuación de la una recta tangente a una curva.
Analizar la razón de cambio entre dos variables
Calcular el área de una superficie y el volumen de un sólido.
El cálculo sustenta su estudio en el conjunto de los números reales, por esta razón es necesario conocer
sus axiomas y sus principales propiedades.
1.1 La recta numerica
La recta numérica es un gráfico unidimensional de una línea recta en la que los números enteros son mostrados
como puntos especialmente marcados que están separados uniformemente. Todos ,los números reales pueden ser
localizados en la recta numérica en los que cada uno es la coordenada de algún punto de la recta.
1.2 Los numeros reales
Los números reales se clasifican de la siguiente manera para su estudio:
Conjunto de Números Naturales(N): Son los números que se utilizan para contar se denota por
N  1,2,3,4,5,6,7,....... Estos son infinitos.
Conjunto de números enteros(Z): Se define el conjunto de números enteros como:
Z  ...... 3,2  1, 0,1,2,3,4,5,......
Conjunto de números racionales (Q): Se define el conjunto de números racionales como:
a

Q   a, b  Z , b  0 
b

Los números racionales se definen como el cociente de números enteros, donde el denominador debe ser ≠ 0. Algunos
ejemplos de números racinales son:
1 4 2 4
, ,  , , 0.121212 ..., 0.25
5 9 3 1
Los números decimales exactos son valores que al momento de resolver el cociente da como respuesta un decimal
finito, ejemplos:
1
3
 0.25,
 1.5
4
2
Los números decimales periódicos son valores que al momento de resolver el cociente da como respuesta un decimal
infinito periódico, ejemplos:

3.4  3. 44444444
,  52.04 52.0404040404
Conjunto de números irracionales(I): Son números que no son racionales, esto es que no son decimales
exactos ni periódicos, algunos ejemplos de ellos son:
 ,e, 2
Conjunto de números reales(R): Se define al conjunto de números reales como la unión de los números racionales e
irracionales. Es decir R  Q  I .
Ejercicio 1: Dados los siguientes valores numericos clasifícalos de acuerdo al conjunto de números reales.
1) 4 __________
__________
__________
__________
__________
__
2)  7 __________
__________
__________
__________
__________
_
3
__________
__________
__________
__________
__________
__
4
2
4) __________
__________
__________
__________
__________
___
7
5)  __________
__________
__________
__________
__________
___
3)
1.3 Propiedades de los numeros reales
Dados dos números reales cualesquiera x y y se define la suma de x  y  R y el producto xyR que
satisfacen los siguientes axiomas:
Propiedad conmutativa de la suma
x y yx
Propiedad asociativa de la suma
x   y  z   x  y   z
Propiedad del neutro aditivo
x0 x
Propiedad del inverso aditivo
x   x   0
Propiedad conmutativa del producto
xy  yx
Propiedad asociativa del producto
x yz  xyz
Propiedad del neutro multiplicativo
x(1)  x
Propiedad del inverso multiplicativo
 
x x 1  1
Propiedad distributiva
x y  z   xy  xz
Ejercicio 2. En los siguientes ejercicios identifica que propiedad se está presentando.
1) 4  3  3  4
__________
__________
__________
__________
2) 7(3  y )  21 7 y __________
__________
__________
__________
_
3) 4( x)  ( x)4 __________
__________
__________
__________
______
4) 4  (9  2)  (4  9)  2 __________
__________
__________
______
5) 7 * (5 * 3)  (7 * 5) * 3 __________
__________
__________
__________
INSTITUTO TECNOLOGICO SUPERIOR DE CAJEME
CALCULO DIFERENCIAL
Nombre ___________________________________________
Matricula ____________
TAREA 1
En los ejercicios siguientes exprese los racionales dados en forma decimal
5
6
14
4.
3
2.
3.
21
4
5, 
4
17
En los ejercicios 10 a 21 escriba los números decimales dados si es posible, en forma de fracción.
11. 3.141615
13. 0.2555555....
15. 5.71715
17. 0.0134134134
19. 0.1231231231
23
21. 4.022022022