CUADRO DE REPASO DE ÁLGEBRA VECTORIAL INTRÍNSECA

CUADRO DE REPASO DE ÁLGEBRA VECTORIAL INTRÍNSECA
Concepto
Definiciones: Álgebra vectorial intrínseca
DEFINICION
Punto, elemento
de un espacio
puntual o afín
En, donde la dim.
n = 2 (plano
puntual) ó n = 3
(espacio puntual)
E2ó3
son
una
representac.
matemática del
espac. o plano
geométricos
ordinarios
(se
consideran como
dato primitivo)
Interpretación geométrica
D
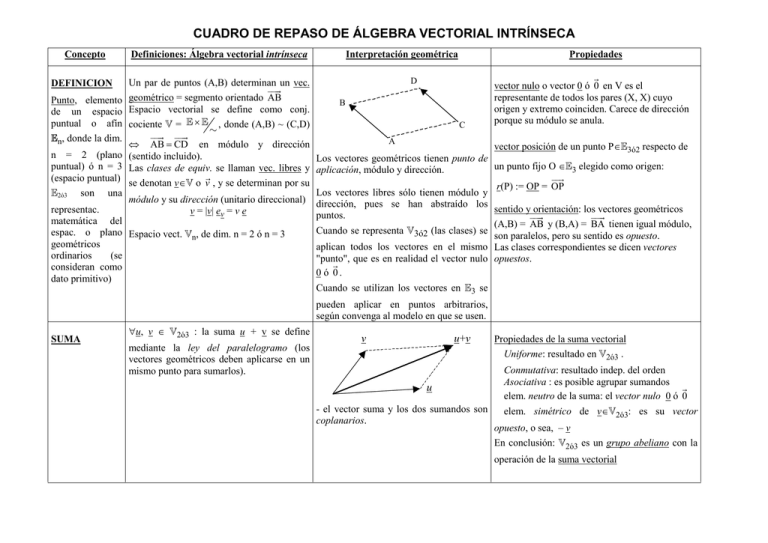
Un par de puntos (A,B) determinan un vec.
uuur
geométrico = segmento orientado AB
B
Espacio vectorial se define como conj.
cociente V = E ´ E , donde (A,B) ~ (C,D)
C
:
uuur uuur
A
Û AB = CD en módulo y dirección
(sentido incluido).
Los vectores geométricos tienen punto de
Las clases de equiv. se llaman vec. libres y aplicación, módulo y dirección.
r
se denotan vÎV o v , y se determinan por su
Los vectores libres sólo tienen módulo y
módulo y su dirección (unitario direccional) dirección, pues se han abstraído los
v = |v| ev = v e
puntos.
Cuando se representa V3ó2 (las clases) se
Espacio vect. V , de dim. n = 2 ó n = 3
n
Propiedades
r
vector nulo o vector 0 ó 0 en V es el
representante de todos los pares (X, X) cuyo
origen y extremo coinciden. Carece de dirección
porque su módulo se anula.
vector posición de un punto PÎE3ó2 respecto de
un punto fijo O ÎE3 elegido como origen:
uur
r(P) := OP = OP
sentido y orientación: los vectores geométricos
uuur
uuur
(A,B) = AB y (B,A) = BA tienen igual módulo,
son paralelos, pero su sentido es opuesto.
aplican todos los vectores en el mismo Las clases correspondientes se dicen vectores
"punto", que es en realidad el vector nulo opuestos.
r
0 ó 0.
Cuando se utilizan los vectores en E3 se
pueden aplicar en puntos arbitrarios,
según convenga al modelo en que se usen.
SUMA
"u, v Î V2ó3 : la suma u + v se define
v
u+v
mediante la ley del paralelogramo (los
vectores geométricos deben aplicarse en un
mismo punto para sumarlos).
u
- el vector suma y los dos sumandos son
coplanarios.
Propiedades de la suma vectorial
Uniforme: resultado en V2ó3 .
Conmutativa: resultado indep. del orden
Asociativa : es posible agrupar sumandos
r
elem. neutro de la suma: el vector nulo 0 ó 0
elem. simétrico de vÎV2ó3: es su vector
opuesto, o sea, – v
En conclusión: V2ó3 es un grupo abeliano con la
operación de la suma vectorial
Teoría de Campos¡
Concepto
MÚLTIPLO
ESCALAR
Sección 1.1: Repaso de álgebra vectorial – CUADRO RESUMEN
Definiciones: Álgebra vectorial intrínseca
Interpretación geométrica
2
Propiedades
Propiedades del múltiplo escalar de vectores
"aÎR, "vÎV2ó3 : au se define por:
es operación R × V ® V
3v
§ su módulo: |a||u|,
§ su dirección: sg(a)eu.
Dados un conj. de n vectores {u, v, w, ...} y
otro de igual núm. de escalares {a, b, g,..},
el vector x = au + bv + gw + ... se llama
combinación lineal de los vect. dados con
los coeficientes escalares dados.
2v
asociativa respe. esc.: (ab)u = a(bu) = (au)b
distributivas tanto resp. suma esc. como vect.:
(a+b)u = au + bu ; a(u + v) = au + av
casos especiales:
"u : 1 u = u , 0 u = 0 ; "a : a 0 = 0
v
-v
Si v = e es un vector unitario (dirección):
PRODUCTO
ESCALAR DE
DOS
VECTORES
"u, v Î V se define el escalar
Propiedades del producto escalar de dos vectores
u
u·v = |u||v|cosq
donde q Î [0 , p] es el ángulo entre u y v
(ángulo barrido en el plano P(u, v) al girar u
hacia v por el sentido más breve)
e
u·e es la proyección ortogonal de u sobre la
dirección e (
es ley de comp. externa (resultado escalar)
Conmutativa: u·v = v·u
Asociativa resp. múltiplo esc.:
(au)·v = u·(av) = a(u·v)
Distributiva: u · ( v + w) = u·v + u·w
casos especiales: vect. ortogonales
p
u ^ v Û u · v = 0 (ángulo q = )
2
u · u = |u|2 = u2 Þ "u : |u| = u·u
Propdes. del producto vectorial de dos vectores
PRODUCTO
"u, v Î 2ó3 : u´v := |u| |v| sena n Î 3,
u´ v
VECTORIAL
DE DOS VECT.
donde n ó eu´v está definido por la ley de la
mano derecha.
El módulo |u´v| es el área del paralelogramo
determinado por u y v
u
a
v
ley del pulgar extendido de la mano derecha,
cuando el resto de dedos se cierran desde el
prefactor hacia el posfactor por el ángulo
menor.
Uniforme :produce nuevos vectores
No conmutativa, sino
Antisimétrica:
u×v=–v×u
No asociativa: u × (v × w) ¹ (u × v) × w
(el primero, se llama triple prod. vectorial)
No existe elemento unidad.
No neutro ni simétrico (o inverso)
Distributiva respecto de la suma:
u × (v + w) = u × v + u × w
Asociativa resp. múltiplo escalar :
(au) × v = u × (av) = a (u × v) = au×v
Casos especiales: u × 0 = 0 × u = 0 , "u
u × v = 0 Û u | | v (vect. paralelos)
Teoría de Campos¡
Concepto
Sección 1.1: Repaso de álgebra vectorial – CUADRO RESUMEN
Definiciones: Álgebra vectorial intrínseca
Interpretación geométrica
TRIPLE PROD "u,v,wÎ , definimos
3
ESCALAR
o
[u, v,w] := u´v · w = u · v´w
PRODUCTO
3
Propiedades
Propiedades del producto mixto o triple producto
escalar de tres vectores en el espacio V3
w
(las mismas que el determinante):
MIXTO (en V3) su valor absoluto representa el volumen del
paralelepípedo determinado por u, v, w.
su signo representa la orientación de la terna
(respecto a la ley de la mano derecha)
v
u
-No uniforme: resultado escalar
-No conmutativa, sino
-Alternada : si p(a, b, c) es una reordenación
(permutación) de la terna (a, b, c) de signatura e,
entonces el producto mixto de p(a, b, c) es
e [a, b, c]
con e = ±1 si la permutación es par/impar (se
admite que e = 0 si p no es una permutación, y
repite algún factor)
- Producto de productos mixtos:
é a ·u
a·v
a ·wù
êë c ·u
c ·v
c ·wúû
[a, b, c] [u, v, w] = det êê b·u b·v b·wúú
-Casos especiales:
[a, b, c] = 0 Û {a, b, c} son coplanarios o
linealmente independientes
a = 0 Þ [0, b, c] = 0 (análogos con b o c)
TRIPLE
PRODUCTO
VECTORIAL
El producto vectorial no es asociativo, pues
a´(b´c) ¹ (a´b)´c
y se llama triple producto vectorial al 1º:
a´b´c := a´(b´c)
(la figura muestra que el triple producto es
una combinación lineal de b y c (pues
pertenece al plano que éstos engendran, al
ser perpendicular a b´c )
c
Se prueba (en componentes) la fórmula del "baccab" o fórmula de expulsión):
a´(b´c) = b(a·c) – c(a·b)
a
a
a´(b´c)
b´c
Otras propiedades se deducen de las del producto
vectorial.
b
Ejercicio: Si a y b son dos vectores dados de V3, de módulos a y b y ángulo á a, b ñ = q, se consideran los sistemas B1 = {a, a´b, b´(a´b)} y B2 = {a, b, a×b}. Se pide:
1º) Discutir si son linealmente independientes y calcular el producto mixto de cada sistema. 2º) Expresar la 2ª base en la 1ª . (Se supone 0 < q < p2 ).
Teoría de Campos¡
Sección 1.1: Repaso de álgebra vectorial – CUADRO RESUMEN
OTROS CONCEPTOS IMPORTANTES DE VECTORES
SUBESPACIOS
Son conjuntos de vectores cerrados resp. a las combinac. lineales de vectores. Son s.v. impropios {0} y V. Además de ellos, según la dim.:
- Rectas vectoriales : Comb. lineales de un solo vector, generador {a} del s.v. Se denota L({a}) = {todos los múlt. esc. de a}
- Planos vectoriales : C. l. de un par de vectores, generadores {a, b}, lin. indeptes.. Se denota L({a, b}) = {todas las c. l. de a y b}
- Subespacio ortogonal a un a dado:
el conj. {a}^ := {xÎV t.q.: a · x = 0} es un plano vectorial en V3 , pero es una recta vectorial en V2.
VECTORLES.
- Subespacio generado por un sistema de p vectores : L({a1, … , ap} es el conj. de todas las c.l. de los vectores del sistema.
Se observa que todos los s.v. de V2ó3 contienen al vector 0, luego todos pasan por el "origen" 0 de V2ó3.
APLICACION
ES LINEALES
Interesan los endomorfismos f : V2ó3 ® V2ó3 , que son las aplicaciones que conservan las c. l., es decir:
f(au + bv) = a f(u) + b f(v) (así: "la imagen de una c.l. de vectores es la c.l. de las imágenes")
También interesan las formas lineales que son aplicaciones lineales f : V2ó3 ® R, que cumplen tamb. la relación anterior, pero con resultado
escalar.
- Se llama núcleo (en alemán kern) de una aplicación lineal f al s.v. ker f = {x Î V2ó3 : f(x) = 0 (ó 0, para formas lin.). El núcleo es
siempre un s.v. si f es lineal.
- Además, si f es un endomorfismo de V2ó3 , el conjunto imagen de f, denotado Im(f), es también un s.v.
Las ecuaciones lineales (ligadas a una apl. lin.) se clasifican en dos grandes tipos: homogéneas y afines o completas, y son de la forma:
f (x) = 0 ® ec. homogénea ; f (x) = a ¹ 0 (ec. afín o completa: x se considera incógnita y a, dato).
- las soluciones de la ec. homogéneas son los vectores del ker f
- las soluciones de la ec. completa son de la forma x = xp + h , donde h Î ker f y xp es una solución particular de la ec. completa (o
sea: si se tiene una sol. part. de la ec. completa, se tienen todas las demás mediante el núcleo de la apl. lin. f que define la ecuación.
EJERCICIOS: pueden hacerse de la PRÁCTICA 1: ejercicios nn. 1 a 3.
OTROS EJERCICIOS:
1) Expresar el ángulo q = á a, b ñ , que forman los vectores dados a y b, en términos intrínsecos de | a |, | b | y | a + b |
2) Descomponer un vector dado a en suma de dos componentes, a1+a2, una según una dirección, dada por un unitario, e, y la otra perpendicular a e.
3) Probar que el conjunto de vectores ortogonales a un vector dado, a, denotado {a}^, es un subespacio vectorial de dimensión n –1, siendo n = 2 ó 3, la
dimensión del espacio V.
_________________________________________________________________________
4