unidad 7: distribución de probabilidad continua

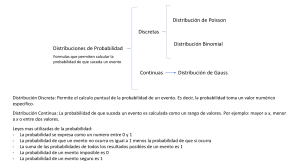
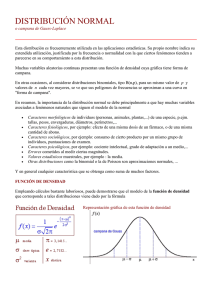
Escuela de Economía – UTPL Estadistica I Autor: Econ. Carlos Correa Granda UNIDAD 7:
DISTRIBUCIÓN DE PROBABILIDAD CONTINUA
Para el desarrollo de este capítulo, vaya
revisando conjuntamente con esta guía el
capítulo 6 del texto básico, págs.223 a la 245.
7.1. DISTRIBUCIÓN DE PROBABILIDAD NORMAL: En la unidad anterior hemos trabajado con las variables discretas y hemos encontrado que se pueden identificar tres tipos de distribuciones, binomial, hipergeométrica y de Poisson, cada una con sus características propias que establecen su aplicabilidad en los diferentes casos. Ahora cuando trabajamos con una variable continua, lo hacemos básicamente con una que es la probabilidad normal. Antes de definir lo que significa esta distribución, haga una revisión de lo que nos dicen los autores del texto, respecto a este tipo de distribuciones de probabilidad, de manera que puede encontrar allí las características de una familia de distribuciones de probabilidad uniforme. Como verá, estas distribuciones se caracterizan por ser simétricas y su representación gráfica tiene la forma de una campana. Al igual que en las distribuciones anteriores, existe una forma de calcular, conforme lo puede establecer en la fórmula 7.4 del texto, sin embargo puede resultar un tanto compleja la aplicación de esta fórmula, de manera que para encontrar una probabilidad se acude al uso de las tablas de áreas bajo de la curva normal. Pero, ¿cómo podemos llegar a determinar una probabilidad de este tipo?, antes de identificar su procedimiento, conviene que definamos a la probabilidad normal, con la lectura del texto usted puede llegar a expresar una definición. Hágalo en su cuaderno de trabajo. Si en su definición ha considerado aspectos tales como: variable continua, forma simétrica o acampanada, que es simétrica con respecto a la media aritmética, entonces podemos decir que estamos en lo correcto. Ahora si, podemos determinar los procedimientos que se requieren para llegar a determinar una probabilidad. 1. La probabilidad normal, se denomina también distribución de probabilidad normal estándar, y por ello se requiere transformar los valores de X en términos de Z, a través de la siguiente fórmula: X‐ µ
Z
σ
Esta obra ha sido licenciada con Creative Commons Ecuador 3.0 de Reconocimiento ‐ No comercial ‐ Compartir igual (http://creativecommons.org/licenses/by‐nc‐sa/3.0/ec/). Escuela de Economía – UTPL Estadistica I Autor: Econ. Carlos Correa Granda 2. El resultado de Z, puede ser negativo y positivo, este signo nos indica la posición del dato con respecto a la media, cabe indicar que en términos de Z la media es igual a cero. 3. Para determinar el área bajo la curva normal a encontrarse es aconsejable realizar un gráfico como el siguiente: 4. Con los valores de Z, pasamos a leer la en la tabla de áreas bajo la curva normal el valor correspondiente, usted puede observar esta tabla en el apéndice B1, del texto básico. Para observar el uso de estas tablas, remítase a los ejemplos desarrollados en el texto, allí usted podrá identificar la forma en la que se puede llegar a determinar los valores de las probabilidades requeridas. En los apartados correspondientes a las aplicaciones de la distribución normal estándar y en la determinación de áreas bajo la curva normal, así como en los ejercicios desarrollados, se encuentra explicado al detalle la forma en la que se puede determinar las probabilidades normales. Realice también las autoevaluaciones previstas de manera que vaya adquiriendo las competencias referidas al cálculo de la probabilidad normal. Estudiemos ahora el caso especial en donde se utiliza la distribución normal cuando la variable es discreta, se trata de la aproximación normal a la binomial. 7.2. APROXIMACIÓN NORMAL A LA BINOMIAL En algunas ocasiones, aunque la variable es discreta, los cálculos de las probabilidades pueden resultar demasiado extensos por el número de observaciones, de allí que otra forma de trabajar este tipo de casos, es utilizando la aproximación de la distribución normal a la binomial. Puede leer en el texto en la página 242 este acápite, pues, allí está explicada la forma en la que se debe trabajar en estos casos. Como ha podido leer, para poder llevar a cabo esta aproximación se requiere previamente realizar una corrección de continuidad. Recordemos que en las distribuciones de probabilidad binomial estamos trabajando con variables discretas que son aquellas que no toman valores intermedios entre uno y otro valor, en cambio la distribución normal trabaja para variables continuas que sí pueden tomar infinidad de valores entre uno y otro. Esta obra ha sido licenciada con Creative Commons Ecuador 3.0 de Reconocimiento ‐ No comercial ‐ Compartir igual (http://creativecommons.org/licenses/by‐nc‐sa/3.0/ec/). Escuela de Economía – UTPL Estadistica I Autor: Econ. Carlos Correa Granda La aplicación del factor de corrección de continuidad, establece cuatro casos que se pueden presentar: 1. Cuando la probabilidad a encontrarse dice que por lo menos ocurra X, se utiliza el área por encima de (X – 0,5) 2. Cuando la probabilidad a encontrarse dice que ocurra más que X, se utiliza el área por encima de (X + 0,5) 3. Cuando vamos a encontrar la probabilidad de que ocurra X o menos, se utiliza el área por debajo de (X + 0,5) 4. Cuando vamos a encontrar la probabilidad de que ocurra menos que X, se utiliza el área debajo de (X – 0,5) Una vez que hemos aplicado la corrección por continuidad, se sigue los pasos que se contemplan para encontrar una probabilidad normal. Revise este apartado en el texto, allí se encuentran explicados los pasos que se deben seguir para trabajar en estos casos. Como podrá analizar usted, hemos llegado a concluir los temas previstos para esta asignatura, espero que le sean de utilidad en su formación profesional, por ello para concluir vamos a recomendarle algunas actividades que le permitirán afianzar más los temas tratados. Luego le propongo una autoevaluación para que confirme su nivel de logro o establezca las acciones correctivas para mejorar sus resultados. Esta obra ha sido licenciada con Creative Commons Ecuador 3.0 de Reconocimiento ‐ No comercial ‐ Compartir igual (http://creativecommons.org/licenses/by‐nc‐sa/3.0/ec/).