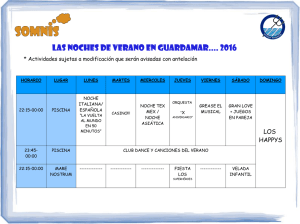
Estirado del POY

Efecto de las condiciones técnicas del proceso de texturizado en las
propiedades de las estructuras lineales textiles
SIP 2007042
RESUMEN
En este trabajo se estudian las propiedades mecánicas y la contracción residual de dos
series de hilos de poliéster texturados, los primeros de título 16.7/68 tex y los segundos de
29.0/138 tex. Los hilos antes mencionados furon procesados en una estiradora industrial de
la casa Barmag a cinco niveles de temperatura (80, 90, 100, 110 y 120°C). En cuanto a la
texturación se utilizó una máquina dobladora de la firma RPR, donde los coeficientes de
torsión tex fue de 64.61, 77.53 para la primera serie de hilos y de 90.45, 85.14, 102.17 y
119.20 para la segunda serie de hilos de poliéster, en torsión Z. Se estudio el
comportamiento viscoelástico a través del modelo de Vangheluwe a los hilos estirados,
también se analizó el histograma de alargamiento utilizando las técnicas del punto conocido
y el algoritmo de Guggenheim. Por otra parte, se ajustó el modelo exponencial a datos de
contracción residual del hilo 16.7/68 tex estirado a diversas temperaturas en la máquina
industrial, se utilizó la técnica de los tres puntos de apoyo de Lipka y el algoritmo de
Guggenheim. Finalmente se establecen las ecuaciones de regresión lineal múltiple para los
propiedades de alargamiento a la rotura (%), fuerza de rotura (cN), Tenacidad de rotura
(cN/tex), módulo inicial (cN/tex), así como contracción residual (%) medido por la técnica
de aire caliente de los hilos texturados en términos de la temperatura y coeficiente de
torsión.
ANTECEDENTES
La orientación molecular que se produce en el proceso de estirado conduce a un incremento
de la cristalinidad del poliéster. El grado de cristalinidad depende del historial temperaturatiempo durante y después de la etapa de estirado, del grado de orientación y del peso
molecular.
Es fundamental que la cristalinidad alcanzada se mantenga constante y en un porcentaje
suficiente para que el producto final tenga una respuesta adecuada y uniforme al
encogimiento térmico y al procesado posterior (tintura, texturado, etc.).
Aunque en el POY no se suele utilizar es reseñable indicar que si el estiraje se aplica en dos
etapas, cada una de ellas con una relación de estirado y temperatura propias, se consiguen
fibras más uniformes, mayor velocidad en el estirado y en general, mejores propiedades
globales, además de constituir una operación muy versátil. Generalmente la relación de
estirado oscila entre 1.6-1.8.
Cuando la relación y temperatura de estirado son elevadas, resulta un hilo con una alta
orientación, y por lo tanto, con una alta cristalinidad. Esto se traduce con unas propiedades
finales tales como bajo alargamiento, baja contracción residual, elevada tenacidad y trabajo
de rotura, además de un módulo elevado. Este hecho pone de manifiesto que se obtendrá un
hilo con una elasticidad baja que tendrá muy posiblemente problemas en los procesos de
hilatura y tisaje.
De ahí la importancia de fijar relaciones de estirado y temperaturas que nos permitan
obtener un hilo óptimo para el proceso al que se vaya a someter.
Por otra parte, del análisis del módulo de los hilos obtenidos, se pueden deducir importantes
consecuencias. Un bajo módulo indica que la fibra o filamento es muy flexible, o sea, a
menor módulo menor rígida es la fibra obtenida. Este hecho indica que las fibras con mayor
flexibilidad aportan también una mayor suavidad, y por lo tanto, mayor confort,
característica que se traslada a los tejidos elaborados con dichos hilos.
Estirado del POY.- Como se ha indicado con anterioridad, el POY obtenido en el proceso
de hilatura posee unas características, tales como estabilidad, fácil almacenamiento, menor
extensibilidad que los hilos MOY, bajo estirado residual, etc., que lo hacen apto para los
procesos posteriores de estirado o estirado-texturaciòn.
Debido a estas características, ha tenido una amplia aceptación en el mercado, siendo el
preferido por la mayor parte de los industriales.
La cristalinidad del hilo POY es baja, Sien embargo ésta se desarrolla durante la etapa de
estirado, generalmente favorecida por la aplicación de tratamientos térmicos.
Para efectuar un correcto y regular estirado del hilo POY, la temperatura de estirado debe
rebasar la temperatura de transición vítrea del Poliéster.
En el proceso de estirado, dos son fundamentalmente los factores cruciales del proceso:
• Relación de estirado. Es la relación entre el título inicial y el título final o la relación
entre la velocidad de recogida y la velocidad de alimentación. Cada hilo POY ha
sido elaborado para obtener un determinado titulo final. La elección entre una u otra
relación de estirado depende de los parámetros que se quiere que cumpla el hilo
estirado, tales como alargamiento, tenacidad, módulo inicial, fuerza de trabajo, etc.
Sin embargo, no es un factor que sea independiente, sino que esta íntimamente
relacionado con la temperatura de estirado, que es el segundo factor importante del
proceso.
• La temperatura de estirado es aquella a al que se calienta el POY para llevar a cabo
el proceso de estirado. La temperatura de estirado debe de ser superior a la
temperatura de transición vítrea para conseguir que el proceso de estirado se lleve a
cabo de un modo uniforme.
La regularidad es mejorada haciendo que el hilo dè varias vueltas alrededor de los cilindros
alimentadores y de los cilindros estiradores, los cuales están bruñidos y tienen asociados
rodillos guía de menor diámetro, cuya función es la de evitar que las espiras evoluciones
conjuntamente.
La temperatura de estirado es un factor que juega un papel importante en las características
del hilo obtenido, sobretodo en lo referente a la contracción residual.
La relación de estirado es, por otra parte muy importante debido a que esta íntimamente
relacionado con el alargamiento final del hilo estirado, en el cuál, un alargamiento óptimo
se sitúa alrededor del 30%.
Estiradora industrial Barman DW24-2.- Esta máquina consta de 24 posiciones que
trabajan conjuntamente como una unidad compacta. Posee la particularidad de transportarse
con facilidad hasta su ubicación definitiva. Puede trabajar inmediatamente tras su conexión
a la red eléctrica y a la instalación de aire comprimido.
Resalta por su sencillez en el momento de efectuar los cambios en le reglaje de
funcionamiento de la máquina para procesar los distintos hilos que se manipulen. Esto
permite una gran rapidez en la elaboración de las experiencias, por lo que es más
importante una enorme velocidad en la localización de los ajustes más idóneos para
procesar los distintos hilos que se puedan estirar.
Puede manipular hilos de titulo comprendidos entre 1-100 tex. La máquina esta compuesta
de un bastidor en cuya parte superior está alojado el equipo de alimentación de los cilindros
de estiraje. Por cada dos posiciones de bobinado de la máquina existe una unidad de estiraje
completa.
VISCOELASTICIDAD
Las fibras consisten principalmente en unidades cristalinas orientadas y exhiben la
viscoelasticidad cuantitativamente como los polímeros amorfos. Llega como sorpresa que
alguien como J. C. Maxwell, quien es mejor conocido por su trabajo en la electricidad y el
magnetismo, contribuyera en las matemáticas de la viscoelasticidad. Cuando estaba usando
una fibra de seda, como elemento de recuperación en un artefacto para medir la carga, noto
que el material no era perfectamente elástico y que mostraba efectos de tiempo. El modelo
que lleva su nombre se propuso para relacionar el comportamiento real de una fibra.
Prácticamente la investigación producida en esta área se encuentra publicada entre los años
50 y los años 90 incluyendo los primeros trabajos de Meredith hasta los trabajos mas
recientes de Vangheluwe, pasando por las recopilaciones de trabajo de varios autores
realizada por Morton y Hearle. La aplicación de un esfuerzo a un material plástico tiene
como primera consecuencia una deformación elástica debida a las deformaciones en las
longitudes y ángulos de enlace. Estas deformaciones son reversibles de pequeña magnitud y
se cuantifican mediante los parámetros elásticos: modulo de compresión, modulo de
rigidez, modulo inicial y relación de Poisson. La relación de Poisson es un parámetro de
interés cuyo valor oscila entre 0.5 para los fluidos y 0 para los sólidos elásticos
incompresibles.
El comportamiento mecánico de los sólidos elásticos se rige por la ley de Hooke, mientras
que el correspondiente a los fluidos viscosos por la ley de Newton para cualquier grado de
deformación. Sin embargo todos lo sólidos reales manifiestan en su comportamiento
mecánico un efecto viscoso y todos los fluidos reales, un efecto elástico. La combinación
de ambos efectos se conoce como viscoelasticidad, la cual esta presente con mayor o
menor énfasis en todos los sólidos y fluidos reales. La viscoelasticidad es la propiedad
distintiva de los materiales plásticos y se define por una respuesta compleja del
comportamiento mecánico fuertemente dependiente del tiempo. La fluencia lenta y la
relajación de la tensión son sus características.
El comportamiento viscoelástico es interpretable sobre la base de la dinámica molecular;
las deformaciones de enlaces y las deformaciones conformacionales reversibles junto con
los deslizamientos moleculares que se producen a grandes deformaciones explican las
recuperaciones, los tiempos de relajación y las deformaciones permanentes que se
observan en los polímeros.
MODELOS ANALÓGICOS CUANTIFICABLES
En líneas generales, una forma de estudiar y definir una ley matemática del
comportamiento viscoelástico es a partir de modelos analógicos cuantificables que nos
permiten extraer magnitudes cuantitativas que le caracterizan, donde la componente elástica
se representa por un elemento de Hooke y por su comportamiento estaría relacionado con
la respuesta instantánea al esfuerzo recibido por la variación de las dimensiones que serian
recobradas totalmente al cesar el esfuerzo. El elemento de Newton explicaría la variación
de dimensiones sin recuperación que se producen a lo largo del tiempo en un material, ya
sea durante la aplicación del esfuerzo o bien después de cesar el mismo, y estaría
relacionado con las tensiones internas acumuladas en el material, que se liberan
gradualmente. Existen diversos modelos analógicos constituidos por los elementos de
Hooke y Newton colocados en serie o en paralelo. La combinación de estos elementos
puede efectuarse como en los modelos de Vangheluwe, etc.
Modelo potencial.- Es el modelo más simple y esta constituido por un único elemento de
Hooke; como se ilustra en la siguiente figura. El modelo potencial cumple la función:
y = A xB
Donde:
y.- es la tensión aplicada sobre el elemento de Hooke
X.- es la deformación que experimenta dicho elemento al someterse a tensión
A.- es el modulo del elemento de Hooke, y
B.- nos indica la desviación de la linealidad de la deformación
La estimación inicial de a y b de este modelo se obtiene mediante mínimos cuadrados
aplicados sobre la nube de puntos experimental que define la curva carga alargamiento del
textil en estudio
Figura 1.- Modelo potencial
Modelo de Maxwell.- El modelo de Maxwell consiste en un elemento de Hooke dispuesto
en serie con un elemento de Newton, como se ilustra en la figura de abajo; representa a un
material que puede responder elásticamente a una tensión aplicada, pero que también
presenta posteriormente flujo viscoso, en esta modelo las dos contribuciones de
deformación son aditivas.
Si el desplazamiento del elemento de Hooke es x1 y el correspondiente al elemento de
Newton es x2, entonces el desplazamiento total de dicho sistema será x:
x = x1 + x2
El elemento de Hooke al estar colocado en serie soporta la misma tensión que le elemento
de Newton por lo que:
y = E x1
Y también
 dx 
y= η 2
 dt 
Para resolver la ecuación, se aplican las transformadas de Carson (variables seguida por la
letra c) en el que las derivadas de transforman multiplicando por una variable auxiliar p,
entonces la ecuaciones anteriores resultan
yc = E x1 c
yc = η p x2 c
La igualdad en la suma de desplazamientos se mantiene también con las transformadas, por
lo tanto:
1
1 
yc = x1 c + x2 c = yc  +

 E ( pη ) 
De aquí resulta
 pη E 
yc = 
 xc
 pη + E 
Realizando la transformada inversa resulta
− E
y = E x exp 
 ( rη )
Es decir

x

y = A x exp( − B x )
La estimación de los parámetros A y B se obtienen aplicando mínimos cuadrados sobre la
ecuación logaritmizada.
y
= A exp( − b x )
x
Evidentemente al despejar el exponente de la expresión y aplicar logaritmos a ambos la dos
queda así:
 y
log  = log A − B x
 x
Figura 2.- Modelo de Maxwell.
Modelo de Maxwell modificado.- La diferencia entre el modelo descrito anteriormente y
el modelo modificado del mismo nombre, es que en el primero el elemento de Hooke es
proporcional a la deformación x. Mientras que en el segundo dicha función de deformación
es potencial x c . Por ello, el modelo resulta el mismo salvo que la variable x del primer
modelo es sustituido por x c en el modificado. Los estimadores iniciales de A y B son los
mismos que en el modelo de Maxwell, pero adicionalmente se deberá de considerar el
estimador del exponente c que debido a la linealidad de la deformación entonces partida de
uno.
(
y = A x c exp − B x c
)
El modelo de Vangheluwe.- Uno de los modelos más sustentables y recientes es el modelo
de Vangheluwe1 que está constituido por un elemento de Maxwell colocado en paralelo con
un muelle no lineal de módulo C. En la figura 3 se representa el modelo de Vangheluwe. La
relación entre la carga σ y el alargamiento γ se rige por la ecuación:
σ = A(1− e − B γ ) + Cγ
2
Donde,
A es la tenacidad en la fluencia, A = η r, siendo r la razón de deformación.
B es el cociente de la inversa del tiempo de relajación del elemento de Maxwell y la razón
de deformación, y
C es el módulo del muelle no lineal.
Asimismo, estos parámetros tienen una relación directa con las propiedades mecánicas y
tintóreas.
Figura 3.- Modelo de Vangheluwe.
Los parámetros de dicho modelo fueron determinados a partir de los siguientes métodos:
•
•
•
•
Método gráfico1
Método iterativo Marquardt3
Método del hiperplano2 y,
Técnica de mínimos cuadrados4
JUSTIFICACIÖN
Se puede definir un hilo texturado como: “Un hilo continuo, con o sin elasticidad, con o sin
torsión, que tiene un aspecto voluminoso como resultado de una ondulación o rizado de los
filamentos que componen dicho hilo”.
Básicamente, los procesos de texturación de fibras termoplásticas (deformables por el
calor) consisten en un tratamiento térmico del hilo hasta alcanzar el estado termoplástico
para a continuación someter los filamentos a una deformación mecánica, fijando las
alteraciones que ha sufrido el hilo en un proceso de enfriamiento.
El proceso de texturación aparece como consecuencia de la búsqueda continúa del aspecto
y cualidades de las fibras naturales a partir de las fibras sintéticas, pero aportando las
ventajas propias de las fibras sintéticas.
Con el proceso de texturación se consiguen hilos con mayor volumen, mayor confort,
mayor poder cubriente, mayor poder absorbente, mejor aspecto y tacto más agradable.
Estas características se deben a la posibilidad de que en el hilo texturado pueda tener mayor
cantidad de aire en su interior, aumentando la sensación de confort y el poder aislante. Por
otra parte, al deformar los filamentos se pasa de filamentos prácticamente planos a
filamentos con una cierta ondulación, lo que mejora el tacto y la suavidad del artículo.
OBJETIVOS
Se estudia la influencia de la temperatura de estirado sobre dos hilos POY de poliéster de
títulos 28.5/68 tex y 48.0/136 tex. Para ello, se estiran los hilos POY a cinco temperaturas
diferentes: 80, 90, 100, 110 y 120ºC, utilizando una estiradota industrial de la casa
BARMAG. Las muestras obtenidas de hilo estirado se someten a un proceso de texturado
en una máquina de la firma RPR, en las que el único parámetro variable es el coeficiente de
torsión, sometiendo alas muestras a tres niveles de torsión: 500, 600 y 700 v/m.
De este modo se analizó la influencia de la temperatura de estirado para una determinada
relación de estiraje y de la torsión que se imparte en el hilo texturado en los distintos
parámetros que caracterizan al hilo (tenacidad, módulo, alargamiento, contracción residual,
etc.) y en el aspecto del hilo texturado que presenta dicho hilo.
Así, del análisis de los parámetros que experimentan un cambio más notable, se estableció
el efecto que puede tener sobre el tejido obtenido, y de este modo, hallar alguna de las
causas que originan variaciones en el tejido.
Uno de los objetivos fundamentales de este trabajo fue producir un hilo de poliéster de alta
torsión mucho más regular y que aporte las mismas prestaciones e incluso mejore las que se
han conseguido con hilos de seda.
EXPERIMENTACIÓN
Las características de los hilos de poliéster POY utilizados se describen a continuación:
Hilo de poliéster POY de 28.5/68 tex, preparado para estirar y obtener un hilo de titulo final
16.7/68 tex.
Hilos de poliéster POY de 28.5/68 tex
Parámetro
Tìtulo (tex)
Draw tensiòn
Uster (%)
Tenacidad (cN/tex)
Elongaciòn (%)
“L” Color
“b” Color
Productor
28.42
102.6
0.710
2.750
128.4
71.70
1.200
Analizado
28.50
103.0
0.740
2.710
127.64
71.50
1.200
Hilo de poliéster POY de 48.0/136 tex, preparado para obtener un hilo de tìtulo final
29.0/136 tex.
Hilos de poliéster POY de 48.0/136 tex
Parámetro
Tìtulo (tex)
Dra. tensiòn
Uster (%)
Tenacidad (cN/tex)
Elongaciòn (%)
“L” Color
“b” Color
Productor
47.816
171.0
0.800
2.510
135.0
71.60
1.200
Analizado
47.77
171.4
0.850
2.440
129.1
71.40
1.300
Los dos hilos POY utilizados 28.5/68 y 48.0/136 tex se estiraron en una máquina DW24-2
Barmag con la relación de estirado adecuada para obtener el titulo final 16.7/68 tex y
29.0/136 tex respectivamente. Durante el proceso de estirado se establece una variable, que
es la temperatura de estirado. Así se realizó el estirado a cinco temperaturas distintas: 80,
90, 100, 110 y 120ºC.
De cada hilo estirado se obtienen cinco muestras distintas, según la temperatura de estirado
a que se ha sometido.
Éstas muestras se someten al proceso de texturado en una máquina GC96FF de RPR a tres
niveles de coeficiente de torsión: 500, 600, y 700 v/m en sentido Z.
Texturado 16.7/68 tex
No.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Temperatura de
estirado (ºC)
80
90
100
110
120
80
90
100
110
120
80
90
100
110
120
Torsión
(v/m)
500
500
500
500
500
600
600
600
600
600
700
700
700
700
700
Texturado 29.0/136 tex
No.
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Temperatura de
estirado (ºC)
80
90
100
110
120
80
90
100
110
120
80
90
100
110
120
Torsión
(v/m)
500
500
500
500
500
600
600
600
600
600
700
700
700
700
700
Así las variables que se tendrán será la temperatura de estirado y el coeficiente de torsión
del hilo texturado.
El número de muestras por cada hilo es de 15, y en conjunto considerando los dos hilos
alimentarios es de 30 hilos.
Dichas muestras se someten a una serie de análisis para establecer el comportamiento de las
variables que se han introducido en el proceso en las características finales del hilo
obtenido.
• Alargamiento (%)
• Fuerza (cN)
• Tenacidad (cN/tex)
• Módulo (cN)
• Contracción residual (%)
PRESENTACIÓN DE RESULTADOS
Hilo poliéster 16.7/68 tex
Propiedades:
Alargamiento (%)
Fuerza (cN)
Tenacidad (cN/tex)
Módulo inicial (cN/tex)
Contracción residual (%)
80
27.36
566.3
33.89
495.4
15.51
Termperatura de estirado (ºC)
90
100
110
27.13
26.84
24.61
594.9
632.8
636.0
40.10
38.92
37.34
546.2
517.7
635.5
11.30
9.900
9.020
Regresiòn lineal simple
Respuesta:
Constante
Alargamiento (%)
36.308
Fuerza (cN)
Tenacidad (cN/tex)
Mòdulo (cN/tex)
Contracción residual (%)
120
23.40
639.6
38.40
1010.3
7.720
Temperatura (ºC)
-0.1044
Hilo poliéster 29.0/136 tex
Propiedades:
Alargamiento (%)
Fuerza (cN)
Tenacidad (cN/tex)
Módulo inicial (cN/tex)
Contracción residual (%)
80
33.64
988.7
38.00
515.2
16.17
Temperatura de estirado (ºC)
90
100
110
29.84
32.21
29.97
977.4
1035.8
1041.5
34.52
36.85
36.42
447.2
445.0
444.7
9.890
8.580
7.250
120
27.32
1028.8
36.51
444.4
6.600
COMPORTAMIENTO VISCOELÁSTICO
Estirado 16.7/68 tex (90°C)
Estirado 16.7/68 tex (80°C)
40
Tenacidad (cN/tex)
30
20
10
30
20
10
0
0
0
5
10
15
20
25
0
30
5
10
15
20
25
30
Alargamiento (%)
Alargamiento (%)
Estirado 16.7/68 tex (100°C)
Estirado 16.7/68 tex (110°C)
40
Tenacidad (cN/tex)
40
Tenacidad (cN/tex)
Tenacidad (cN /tex)
40
30
20
10
0
30
20
10
0
0
5
10
15
20
Alargamiento (%)
25
30
0
5
10
15
Alargamiento (%)
20
25
Estirado 16.7/68 tex (120°C)
Estirado 29.0/136 tex (80°C)
40
30
Tenacidad (cN /tex)
Tenacidad (cN /tex)
40
20
10
30
20
10
0
0
4
8
12
16
20
0
24
0
Alargamiento (%)
20
30
40
Alargamiento (%)
Estirado 29.0/136 tex (100°c)
Estirado 29.0/136 tex (90°C)
40
40
Tenacidad (cN/tex)
Tenacidad (cN/tex)
10
30
20
10
0
30
20
10
0
0
10
20
30
Alargamiento (%)
40
0
5
10
15
20
Alargamiento (%)
25
30
Estirado 29.0/136 tex (120°C)
Estirado 29.0/136 tex (110°C)
40
Tenacidad (cN /tex)
Tenacidad (cN/tex)
40
30
20
10
0
0
5
10
15
20
25
30
20
10
0
30
0
Alargamiento (%)
5
10
15
20
Alargamiento (%)
Método gráfico
Poliéster estirado 16.7/68 tex (80°C)
Poliéster estirado 16.7/68 tex (90°C)
Poliéster estirado 16.7/68 tex (100°C)
Poliéster estirado 16.7/68 tex (110°C)
Poliéster estirado 16.7/68 tex (120°C)
Poliéster estirado 29.0/136 tex (80°C)
Poliéster estirado 29.0/136 tex (90°C)
Poliéster estirado 29.0/136 tex (100°C)
Poliéster estirado 29.0/136 tex (110°C)
Poliéster estirado 29.0/136 tex (120°C)
A
22.000
12.000
12.000
12.000
10.000
20.000
20.000
24.000
10.000
26.000
B
0.2597403
0.5555556
0.4761910
0.6666667
1.000000
0.250000
0.340000
0.185185
0.5714286
0.1538461
C
0.017752
0.041600
0.045139
0.041667
0.049587
0.015625
0.017857
0.013333
0.035503
0.016000
25
30
Vangheluwe (16.7/68 tex, 90°C)
Vangheluwe (16.7/68 tex, 80°C)
40
Tenacidad (cN/tex)
Tenacidad (cN/tex)
40
30
20
10
30
20
10
0
0
0
5
10
15
20
25
0
30
5
15
20
25
30
Alargamiento (%)
Alargamiento (%)
Vangheluwe (16.7/68 tex, 110°C)
Vangheluwe (16.7/68 tex, 100°C)
40
Tenacidad (cN /tex)
40
Tenacidad (cN/tex)
10
30
20
10
30
20
10
0
0
0
5
10
15
20
Alargamiento (%)
25
30
0
5
10
15
Alargamiento (%)
20
25
Vangheluwe (16.7/68 tex, 120°C)
40
30
30
Tenacidad (cN/tex)
40
20
10
20
10
0
0
0
10
20
30
0
40
4
8
12
16
20
24
Alargamiento (%)
Alargamiento (%)
Vangheluwe (29.0/136 tex, 90°C)
Vangheluwe (29.0/136 tex, 100°C)
40
40
30
Tenacidad (cN/tex)
Tenacidad (cN /tex)
Tenacidad (cN/tex)
Vangheluwe (29.0/136 tex, 80°C)
20
10
0
0
5
10
15
20
Alargamiento (%)
25
30
30
20
10
0
0
10
20
30
Alargamiento (%)
40
Vangheluwe (29.0/136 tex, 110°C)
Vangheluwe (29.0/136 tex, 120°C)
40
Tenacidad (cN /tex)
Tenacidad (cN/tex)
40
30
20
10
5
10
15
20
25
20
10
0
0
ECUACIONES
DE REGRESIÒN
0
30
0
30
5
10
15
20
25
30
Alargamiento (%)
Alargamiento (%)
Hilo poliéster 16.7/68 tex
Alargamiento
(%)
Fuerza (cN)
Tenacidad
(cN/tex)
Módulo
(cN/tex)
Contracción
residual (%)
Coeficiente
de torsión
(v/m):
500
600
700
500
600
700
500
600
700
500
600
700
500
600
700
Temperatura de estirado (ºC)
100
110
80
90
28.46
28.63
22.70
705.9
699.4
638.5
38.80
38.87
35.61
181.7
110.8
100.7
6.100
5.800
4.050
26.00
22.79
26.88
696.6
661.7
681.6
39.28
37.40
37.53
196.8
133.8
104.8
5.600
5.200
3.620
27.21
22.52
22.08
721.6
670.4
649.0
40.10
38.07
36.52
218.7
138.9
107.0
5.200
4.600
3.200
26.54
21.66
21.57
721.0
659.7
643.5
39.52
36.90
35.82
231.1
137.3
109.0
4.920
4.400
2.900
120
25.34
21.31
21.30
695.7
659.5
625.5
39.93
37.08
35.73
227.7
150.0
109.1
4.650
4.100
2.600
Alargamiento
(%)
Coeficiente
de torsión
(v/m):
500
600
700
500
600
700
500
600
700
500
600
700
500
600
700
Fuerza (cN)
Tenacidad
(cN/tex)
Módulo
(cN/tex)
Contracción
residual (%)
80
Hilo poliéster 29.0/136 tex
16.7/68 tex
Temperatura de estirado (ºC)
90
100
110
37.71
36.63
37.70
1157.8
1106.9
1059.6
36.35
34.55
32.66
150.0
112.0
26.18
6.100
5.300
3.400
33.81
32.59
36.85
1122.4
1088.8
1114.6
35.61
34.78
34.96
169.8
111.9
38.77
5.400
4.000
2.760
35.67
38.71
39.27
1153.4
1161.7
1138.3
36.70
36.80
36.03
190.9
124.6
36.66
4.900
3.620
2.320
34.70
38.51
39.10
1145.0
1170.9
1149.3
36.18
37.39
36.02
197.9
137.9
54.04
4.300
3.450
1.950
120
34.07
37.19
36.93
1136.4
1157.7
1118.0
36.35
36.60
33.46
201.9
153.7
52.58
3.920
3.200
1.360
Aplicación de la técnica del punto conocido.No.
Alargamiento
(%)
x
In ( f 14.0 )
x − 26.4
1
2
3
4
5
23.0
23.5
24.0
24.5
25.0
0.453072071
0.431987230
0.184096980
-0.036312037
-0.179510306
No.
Alargamiento
(%)
X
In ( f 14.0 )
x − 26.4
6
7
8
9
10
25.5
26.0
26.5
27.0
27.5
-0.551596540
-0.763454124
-6.931471806
-1.716032362
-1.769009226
x = 25.211702
s = 0.75085599
A = 74.0191446
( 18 )
Optimizando por el método Marquardt, llegamos al modelo numérico funcional siguiente:
f = 21.6539 exp
−
1  x − 25.3183 


2  0.959767 
2
( 19 )
De donde la varianza residual es de 3.99024 y un coeficiente de determinación de
94.6337%.
Ajuste del modelo normal
24
Frecuencia (No.)
20
16
12
8
4
0
23
24
25
26
27
28
Alargamiento (%)
Aplicación del algoritmo de Guggenheim.-
Alargamiento (%)
x
23.0
23.5
24.0
24.5
25.0
Alargamiento (%)
x´
25.5
26.0
26.5
27.0
27.5
Frecuencia (f)
Y
3
4
9
15
18
Frecuencia (f´)
y´
23
19
7
5
2
x´- x = τ
2.5
2.5
2.5
2.5
2.5
Transformación contra “x”.
Alargamiento (%)
Loge (f´/f)
X
23.0
2.03688193
23.5
1558144620
24.0
-0.25131443
24.5
-1.09861229
25.0
-2.19722458
A = 20.0692561
x = 25.2543034
s = 5.69776107
( 15 )
Los valores numéricos anteriores son los obtenidos por el algoritmo de Guggenheim,
dichos valores numéricos son convergentes a los valores óptimos obtenidos por un método
iterativo como se comprueba en la ecuación numérico-funcional (16):
f = 21.6520 * exp
−
1  x − 25.31820 


2  0.9600170 
2
( 16 )
La varianza residual es de 1.54726 y el coeficiente de correlación de 98.509 lo cual señala
un excelente ajuste.
Ajuste al modelo normal
24
Frecuencia (No.)
20
16
12
8
4
0
23
24
25
26
27
28
Alargamiento (%)
CONTRACCIÓN RESIDUAL (%).
La determinación de la contracción residual puede obtenerse por cuatro procedimientos:
• Tube Test New
• Heberlein Tester
• HATRA Crimp Rigidity Test
• Contracción por aire caliente
Contracción residual de hilo de poliéster estirado (tìtulo 16.7./68 tex).
Temperatura de
estirado (ºC)
80
85
90
95
100
105
110
115
120
130
140
150
160
170
180
Contracción residual
(%)
15.59
13.09
10.72
9.94
9.14
8.01
7.97
7.71
6.45
6.40
6.36
5.31
4.86
4.74
3.89
A = 49.5000056
B = − 0.02119342
C = 3.22096498
( 31)
Los valores numéricos anteriores fueron obtenidos aplicando el algoritmo de Guggenheim
y son considerados estimadores iniciales convergentes a una regresión no lineal utilizando
un método de optimización.
En la expresión (32) se muestran los mismos parámetros del modelo exponencial pero están
optimizados por el método Marquardt6. Éstos últimos en relación a los obtenidos por el
algoritmo de Guggenheim requieren solo 4 iteraciones
Cr = 70.9556 exp − 0.025449 t + 3.65408
( 32)
En la tabla 3 aparece el correspondiente análisis de varianza del ajuste de (32), de donde se
destaca que el coeficiente de determinación es significativo al 1% de confianza estadística,
y suma de cuadrados y varianza residual mínimos.
Análisis de varianza de la regresión no lineal por el método Marquardt
Causa
Suma de
Grados de
Cuadrado
Cuadrados
libertad
Medio
Modelo
Residual
Total
Total (corr.)
R2
R2 (con grados de
libertad)
887.672
1.13067
888.803
144.30
99.2164%
99.0423%
3
9
12
11
295.891
0.125629
CONCLUSIONES
Se puede concluir lo siguiente:
Hilo POY estirado.
• Cuanto mayor es el tìtulo POY, mayor es el valor de alargamioento obtenido en el
campo de temperatura experimental
• Tanto para el hilo 29.0/136 tex como para el hilo 16.7/68 tex, a medida que se
incrementa la temperatura de estirado disminuye el valor de alrgamiento.
• La influencia de la temperatura de estirado es màs significativa en la fuerza de
rotura para el hilo 16.7/68 tex.
• Para ambos hilos la temperatura crìtica de estirado es de 100ºC. A temperaturas
superiores, la influencia de latemperatura debe considerarse en funciòn de las
caracterìsticas del hilo deseado: menor alargamiento y mayor resistencia o
viceversa.
• El comportamiento mecànico del hilo 16.7/68 tex en funciòn de la temperatura de
estirado no presenta variaciones significativas.
• El mòdulo de elasticidad calculado al 2.5% de deformación a partir de la
temperatura de estirado de 100ºC aumenta significativam,emte en el titulo 16.7/68
tex. En el titulo 29.0/136 tex disminuye para temperaturas superiores de 80ºC,
permaneciendo aproximadamente constante para temperaturas superiores.
• El valor de la contracción resisdual disminuye con el incremento de la temperatura
de estirado.
El presente estudio permite formular las siguientes conclusiones:
•
El ajuste del modelo normal a datos de vida media de agujas de coser en
condiciones industriales estándar es adecuado considerando el 1% de confianza
estadística que se logra.
En relación a la técnica del punto conocido aplicado a la normal puede decirse lo siguiente:
• La técnica no da respuesta unívoca ya que la curva de ajuste que se obtiene al final
depende del punto que se escoge a voluntad y también de la curva de campana
trazada inspectivamente.
• No obstante lo anterior, la técnica siempre suministra estimadores altamente
convergentes con los optimizados por el método iterativo Marquardt.
En relación al algoritmo de Guggenheim:
• El algoritmo modificado de Guggenheim permite estimar valores convergentes al
modelo normal expuesto en este documento, sin necesidad del uso de métodos de
regresión no lineal ni de equipo de cómputo.
• A pesar de lo antiguo del algoritmo, continua vigente su utilidad fundamentalmente
por lo sencillo de su aplicación y la bondad de sus ajustes.
BIBLIOGRÁFIA
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
Gacén, J.; (1991), “Fibras de poliéster”, 2da Edición, Universidad Politécnica
de Cataluña.
Naik, A.; (1991), “Hilatura técnicas actuales”, 1era Edición, Universidad
Politécnica de Cataluña.
Gacén, J. y Maillo, J.; (1996), “Variaciones de la estructura fina de las fibras
de poliéster en los tratamientos térmicos”, 1era Edición. Universidad
Politécnica de Cataluña.
Información Técnica firma RPR; (1995).
Catalogo técnico de Barman; (1994).
Stein; (1981), “Comprobación de las diferencias en las condiciones de hilatura
en los hilados de poliéster”, ITB 3/81.
Isaac, G. E.; (1991), “Desarrollos en la tecnología de texturado por falsa
torsión”, Técnica Textil Internacional 2/1991.
Catálogo técnico de Zinder; (1996).
Guggenheim, E. S., (1926), Phil. Mag., 1, 538.
Marquardt, D. W., (1963), “An Algorithm for Least-Squares Estimation of
Nonlinear Parameters”, Journal for the Society of Industrial and Applied
Mathematics, 11:431-41.
Vangheluwe, L., (1992), “Study of the Time Dependent Mechanical Properties
of Yarns for Weaving”, Doctoral Thesis, University of Ghent, Belgium.
Guillén, G., Olvera, M., Islas, A. M., y Mercado, L., (2005), “Método numérico
aplicado a la simulación viscoelástica de hilos textiles”, XXXVII Congreso
Nacional de la SMM, Sociedad Mexicana de Matemáticas, Proceeding.
Guillén, G., Islas, A. M., y Guillén, E., (2005), “El valor didáctico del
algoritmo de Guggenheim en la modelización estadística“, XVII Encuentro de
Investigación Científica y Tecnológica del Golfo de México, Academia
Tamaulipeca de Investigación Científica y Tecnológica A. C., Tampico,
Tamaulipas, México. Proceeding.