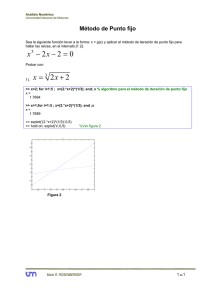
NGJ/v06 Unidad IV 1 Métodos numéricos y álgebra lineal CB00851
Anuncio
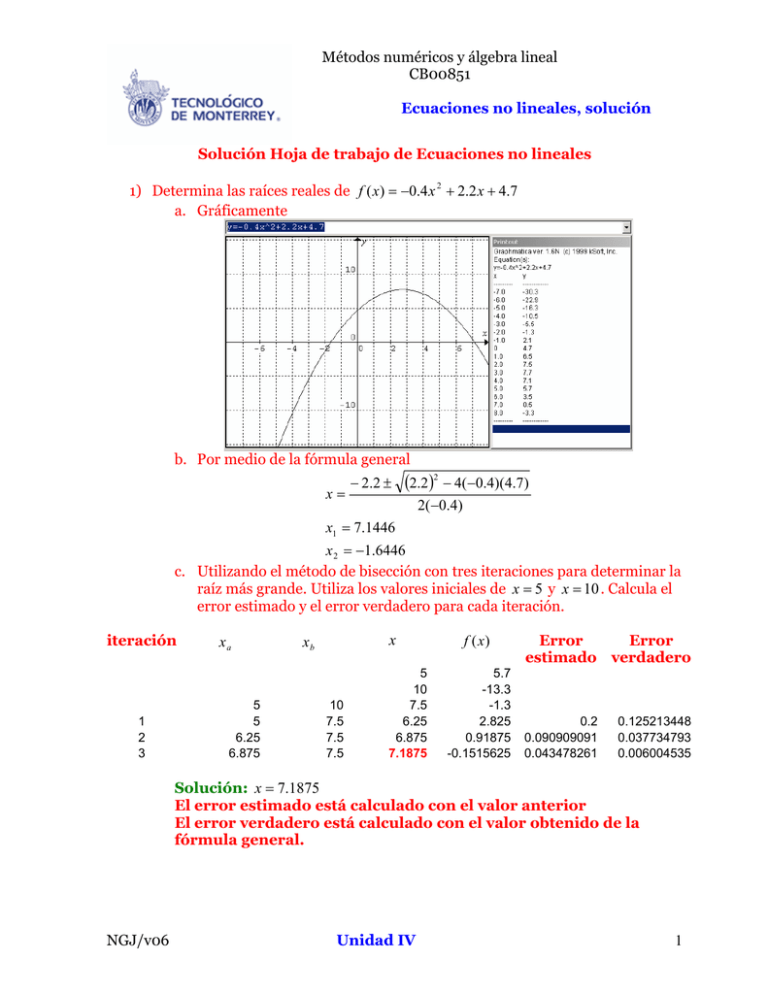
Métodos numéricos y álgebra lineal CB00851 Ecuaciones no lineales, solución Solución Hoja de trabajo de Ecuaciones no lineales 1) Determina las raíces reales de f ( x) = −0.4 x 2 + 2.2 x + 4.7 a. Gráficamente b. Por medio de la fórmula general x= − 2 .2 ± (2.2 )2 − 4(−0.4)(4.7) 2(−0.4) x1 = 7.1446 x 2 = −1.6446 c. Utilizando el método de bisección con tres iteraciones para determinar la raíz más grande. Utiliza los valores iniciales de x = 5 y x = 10 . Calcula el error estimado y el error verdadero para cada iteración. iteración 1 2 3 xa 5 5 6.25 6.875 x xb 10 7.5 7.5 7.5 5 10 7.5 6.25 6.875 7.1875 f (x ) 5.7 -13.3 -1.3 2.825 0.91875 -0.1515625 Error Error estimado verdadero 0.2 0.090909091 0.043478261 0.125213448 0.037734793 0.006004535 Solución: x = 7.1875 El error estimado está calculado con el valor anterior El error verdadero está calculado con el valor obtenido de la fórmula general. NGJ/v06 Unidad IV 1 Métodos numéricos y álgebra lineal CB00851 Ecuaciones no lineales, solución 2) Resuelve por el método de punto fijo e x − tan x = 0 . Determina una g (x ) y un valor inicial x 0 tales que g ( x0 ) < 1 . e x − tan x = 0 e x = tan x Solución: iteración x x = tan −1 (e x ) g ( x) = tan −1 (e x ) x0 = 1 g (1) = 0.443 f (x ) error 1 1.21828291 1.28325462 1.30044736 1.3048397 1.30595146 1.30623219 1.30630303 1.30632091 0 1 2 3 4 5 6 7 8 1.160874104 0.663094773 0.226987884 0.062574053 0.016159474 0.004101426 0.001036379 0.000261587 6.60069E-05 0.17917259 0.05063041 0.01322064 0.00336619 0.0008513 0.00021492 5.4233E-05 1.3684E-05 g (x ) 1.21828291 1.28325462 1.30044736 1.3048397 1.30595146 1.30623219 1.30630303 1.30632091 1.30632542 Una solución está en x = 1.30632091 3) Resuelve por el método de la secante y posición falsa x log x − 10 = 0 ¿Cuál es la diferencia? ¿Cuál método es más exacto para esta ecuación? (x − x ) f ( xi ) xi +1 = xi − i i −1 Solución SECANTE: f ( xi ) − f ( xi −1 ) iteración x 0 1 2 3 4 5 8 9 10.0354646 9.99943638 9.9999997 10 error f (x ) -2.7752801 -1.41181742 0.05089403 -0.0008084 -4.3332E-07 3.6984E-12 0.10318054 0.00360303 5.6332E-05 3.0211E-08 xm = x D − Solución REGULA FALSI: xD f ( xD ) iteración 1 2 3 4 NGJ/v06 9 9.98482733 9.99978064 9.99999683 9.99999995 xI -1.41181742 -0.02175707 -0.00031462 -4.5454E-06 -6.5668E-08 11 11 11 11 11 Unidad IV (x D − x I ) f (x D ) f (x D ) − f (x I ) f ( xI ) xm 1.45531954 1.45531954 1.45531954 1.45531954 1.45531954 9.98482733 9.99978064 9.99999683 9.99999995 10 f ( xm ) -0.02175707 -0.00031462 -4.5454E-06 -6.5668E-08 -9.487E-10 error 0.00149536 2.1619E-05 3.1233E-07 4.5123E-09 2