Catión r Li 0.76 Å Na 1.02 Å K 1.38 Å Rb 1.49 Å Cs 1.70 Å Anión r F
Anuncio
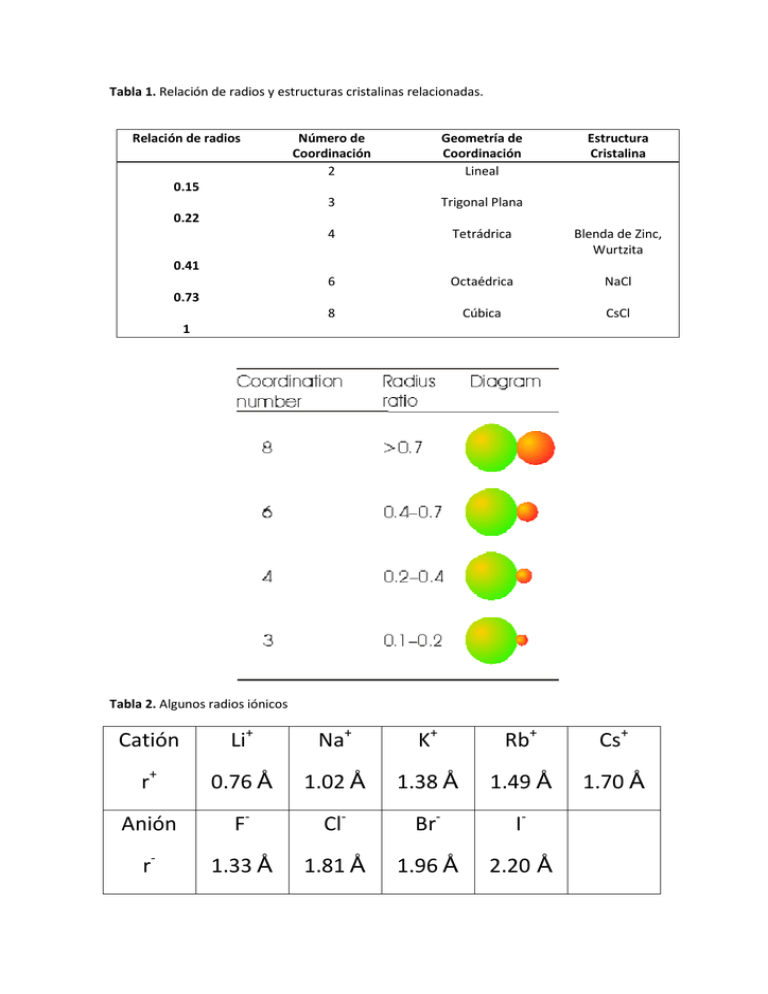
Tabla 1. Relación de radios y estructuras cristalinas relacionadas. Relación de radios Número de Coordinación 2 Geometría de Coordinación Lineal Estructura Cristalina 3 Trigonal Plana 4 Tetrádrica Blenda de Zinc, Wurtzita 6 Octaédrica NaCl 8 Cúbica CsCl 0.15 0.22 0.41 0.73 1 Tabla 2. Algunos radios iónicos Catión Li+ Na+ K+ Rb+ Cs+ r+ 0.76 Å 1.02 Å 1.38 Å 1.49 Å 1.70 Å Anión F- Cl- Br- I- r- 1.33 Å 1.81 Å 1.96 Å 2.20 Å Algunas Estructuras tipo Aspectos Energéticos Sistema formado por 2 cargas 4 Sistema formado por una hilera de cargas alternas +, - 2 2 2 4 4 2 4 3 2 1 1 1 1 2 3 4 4 2 2 4 4 A = cte que depende de la estructura: Cte de Madelung Para un mol de iones (N = NA = 6.023 1023 mol-1) | | 4 Z+ = carga del catión Z- = carga del anión r0 = suma de radios iónicos = r++rBorn-Landé Considera repulsiones electrón-electrón y núcleonúcleo | | 1 1 4 n = exponente de Born, depende de la configuración electrónica y está tabulado átomo Configuración e- n He 1s2 5 Ne [He]2s2p6 7 Ar [Ne]3s2p6 9 Kr [Ar]4s2p6 10 Xe [Kr]5s2p6 12 ε0= permitividad del vacío = 8.854 10-12 jC2m-1 e = carga del electrón = 1.602 10-19 C para no cometer errores introducir todas las constantes y parámetros en el Sistema Internacional (SI), así el resultado sale directamente en julios/mol. La única dificultad está en poner adecuadamente la distancia de equilibrio r0, que normalmente se da en Angstroms y hay que pasarla a metros (1 Å = 100 pm= 10-10 m). Entonces una distancia de equilibrio de 3.14 Å debemos introducirla como 3.14 10-10 m, y todo debe salir bien. El exponente de Born para iones con diferente configuración electrónica que están en la misma sal se promedia, de tal manera que podemos tener para sales del tipo 1/1 nsal = 0.5* (ncatión+nanión) Ciclo de Born-Haber El ciclo de Born-Haber nos permite determinar de una forma indirecta las energías reticulares de los compuestos iónicos (incluso de aquellos que no existen). Básicamente consiste en plantear la ley de Hess para la formación de un compuesto iónico. Al plantear el ciclo partimos de los elementos en su estado estándar y terminamos con el compuesto iónico formado. Podemos establecer dos caminos para estudiar la formación del compuesto; uno iría directamente a la formación y nos daría ∆ !"#$%ó& , pero podemos establecer otra ruta que considere la sublimación o atomización del metal (∆# ), la disociación del halógeno '∆( ), La ionización del metal al estado de oxidación correspondiente (∆) ), la afinidad electrónica del halógeno (AE) y finalmente la formación del compuesto iónico a partir de los iones en estado gaseoso que nos daría la energía reticular, U. Según la ley de Hess el cambio de entalpía total es independiente del camino seguido, por lo que podemos igualar los dos procesos ∆H formación = ∆H sublimación + ½ ∆H disociación + ∆H ionización + AE + U Y despejando U, nos queda U = ∆H formación – ∆H sublimación – ½ ∆H disociación – ∆H ionización – AE De todas las magnitudes que en el ciclo aparecen, U es la única que no se puede determinar de forma directa. Mediante este ciclo, se puede calcular. Una vez obtenida U de forma indirecta a partir de medidas experimentales, se puede comparar con U obtenida de forma teórica a partir de ecuaciones del tipo Born-Landé. Ejemplo de problema Determina la energía reticular [U] para el CsI a partir de los siguientes datos experimentales. Entalpía de formación del CsI: ∆Hf= -346.6 Kj/mol. Energía de atomización/vaporización/sublimación del Cs: ∆Ha= 76.1 Kj/mol. Energía de Ionización del Cs: EI = 375.8 Kj/mol. Entalpía de disociación del I2: ∆HD= 213.6 Kj/mol. Afinidad electrónica del yodo: AE = -295.2 Kj/mol. U = -346.6 - 76.1 - 375.8 - 0.5 *( 213.6) + 295.2 = -610.1 Kj/mol











