Ejercicios y problemas (páginas 244/245) Soluciones

Ejercicios yproblemas (páginas 244/245)
Soluciones
11. Terminaciones que den múltiplo de 4 ~ 12,24,32
p(4) = casos favo~ables = 3 oV2, , = ~ = ~ = O 25
1. ((roja) = 0,5, {(verde) = 0,3, ((blanca) = 0,2
casos posibles
V4, 3
24 4
'
Terminaciones que den múltiplo de 3 ~ 123 Y234 en
cualquier orden dan múltiplo de 30
2. ((azules) = 0,25, ((amarillo) = 0,125, ((verdes) = 0,625
p(3) = casos favorables
casos posibles
NoO de bolas: azules = 50, amarillas = 25, verdes = 125
c
2 oP3 = ~ = 0,5
V4 , 3
2
0 0
o
(100) 100 99 98
12. Casosposlbles= 3 = 3 02 01 =161700
3. Casos posibles = 5! = 120
Casos favorables = 2 o4! = 48
2
48
p= 120 ="5=0,4
Casos favorables = C75 ,1 oC25,2 + C75, 2 oC25, , + C75 , 3 =
= 159400
159400
4. Casos posibles = 6! = 6 o5 o4 o3 o2 o1 = 720
Casos favorables = 2 o4! o5 = 240
240 1
p= 720 =3=0,33
5. Por la primera ley de Morgan: A U B = An B
1594
p= 161700 = 1617 = 0,99
642
2
13. aJ p(A, B, C) = - o- o- = - = 0,036
12 11 10 55
p(uno de cada partido) = 6 o0,036 = 0,22
p(A n B) = p(A U B ) = 1 - p(A U B) =
6. p(A
n
+ p(B) -
4
10
1
bJ p(3deIA)=-0_0-=-=009
11
'
eJ p(3 del C) = O
B) = p(A U B ) = 1 - p(A U B) =
= 1 - [p(A)
n B)] =
p(A
=1-[~+~_~J=37 =06167
34560
7. aJ
6 5
12 11
[~+.¡] = 152 = 0,4167
= 1- [p(A) + p(B)] = 1 -
14.
'
(~o
~ o~) o6 = ~4
= O25
10 9 8
'
bJ p(3 gripe) = ~ o~ o~ = ~ = O083
10 9 8
3
dO
3
12
2
'
1
1
P( po Igestlvos = W09°S= 120 = 0,0083
o
)
p(3 alergias) = O
o
1
1
11
+== O916
12 120 120
'
p(3 el mismo problema) = -
e
O
dO
222
8
8 • P(ninguna a su estlno) = -0-0_=-= O2963
'
3 3 3 27
p(alguna a su destino) = 1 -
~ = ~ = 0,703 7
27
27
2
9. p(l)=-=O,4
5
-F -F) - casos favorables
C'20,2
357
o
=--=-=0,36
casos posibles
C2oo, 2 995
(
a J p,
bJ
(C
p
,
q = casos favorables
casos pOSI°bl es
ClO2.2
5151
-=--=0,26
C2OO,2 19900
vi
.;
oC:
tU
o.
.n
~
694
p(2) = W 0"4 =
N
8N
.i.
~
~
15 = 0,267
Q.
eJ p(solo castellano) =
~
.~
6 5 4 1
p(3) =W 09°S="6=0,167
_ C56,2 + C56" oC24, 1 + C56,1 oC22 ,1 + C24" oC22 ,'
C2oo, 2
p(antes del 4) = 0,83
1161
= 4975 = 0,23
<11
>
'2
::J
"E
~
o
g
w
'dO
) casos favorables C128 2
= --' =
dJ P(so Io 1 I loma =
10. aJ Casos posibles = ClO, 2 = 45
casos posibles
1
Casos favorables = 5 ~ P = - = 0,11
9
2032
= 4975 = 0,408
~
eJ p(los tres idiomas) = O
y
e...o
ii2
5
~p=-=056
9
'
Probabilidad
~
¡¡:
o
u
-'
bJ Casos favorables = 25 ~
_
C2oo,2
-'
111
Estadística
w
~
::¡¡
(
21. aJ 0,5 probabilidad a priori.
5
15. aJ p(l) = 1 - (++ 11 ) = 12 = 0,42
2
1
1
1
bJ p(par) =6"+6"=3=0,33
')
5
1
p(E) . p(G/E)
0,5 . 0,5
p(G)
= 0,5 . 0,5 + 0,5 ' 0,1 =0,83
bJ p(E/G) =
eJ Las nuevas probabilidades a priori son 0,75 y 0,25.
7
e} p (rOJo = U + 6" = U = 0,583
p
dJ p(impar/rojo) = 1
E/GG)
(
0,75' 0,5
=0,94
0,75 . 0,5 + 0,25 . 0,1
p(E) .(i..GG/E)
_ _""""'---_-C--_ _
fi..GG)
dJ Si pierdes es preferible cambiar de máquina.
99
100
p(defectuoso) = 1- 0,955 6 =
.
16. p(n1nguna defectuosa) = -
98,5 98
.- - . = 0,955 6
100 100
0,044
22. p(alarma) = p(avería) . p(alarma/avería) +
+ p(no avería) . p(alarma/no avería) =
= 0,001 . 0,99 + 0,999 ' 0,003 =0,004
bJ
p(l. a pieza
p(alarma/avería) . p(avería) = 0,99' 0,001
defectuosa/aparato defectuoso) =
p(alarma/avería) . p(avería)
( I
)
p a arma
0,99' 0,001
= 0,001 . 0,99 + 0,999 . 0,003 = 0,25
p(averfa/alarma) =
2
3 100
1 1
1 1,5
1 2 = 9 = 0,22
-.-+-.-+-.3 100 3 100 3 100
23. p(60
17. Casos favorables = 7
Casos posibles = 28
p(mayores de 5) = -
7
1
28
p(múltiplos de 3) =
n 10) = p(60) = 0,5
p(60/10) = 0,5/0,78 = 0,64
24. p(se estropeen los dos motores) = 0,005 . 0,005 =
= - = 0,25
4
= 2,5 '10- 5
~: =0,46
p(se estropeen los tres motores) =
= 0,005 . 0,005 . 0,005 = 1,25' 10- 7
18. 1
< : 3 / 4 ByA
3/5 .. A
1/4
1
Cy A
< : 6 / 7 AyB
6/7 • A
p(efectuar aterrizaje de emergencia en bimotor) =
= 1 - (0,005)2
3/5 • A
p(efectuar aterrizaje de emergencia en cuatrimotor) =
= 1 - (0,005)4 - (0,005)3 - (0,005)2
3B~AyC
1/7
p(se estropeen los cuatro motores) =
= 0,005 . 0,005 . 0,005 . 0,005 = 6,25 . 10-10
3A~ByC
Es más seguro un cuatrimotor.
Cy B
6/7
•
A
25. A = obtener 2 premios en las 12 primeras extracciones.
B = el último premio en la extracción número 13.
casos posibles =
c~) =
casos favorables = (;).
11
19. p(~/ecografíal~) = 10 + 11
11
21
10
10
=10+ 11
21
41
41
p(~/ecograffad')
38 + 41
79
38
38
p(d'/ecograffad') =
=38 + 41
79
11 + 38
49
p(acierte)
100
100
p(d'/ecograffa~)=
20 p(enfermo/negativo) = _1_
10000
1
p(enfermo/positivo) = 100
p(enfermo) = p(negativo) . p(enfermo/negativo) +
+ p(positivo) . p(enfermo/positivo) =
99
1
1
1
199
= 100 . 10000 + 100 . 100 = 106 = 0,0002
455
(~~) = 198
198
Por tanto, p(A) = 455 = 0,435.
Quedan en la bolsa: tres bolas: una blanca y dos
negras:
1
p(BIA)=-
3
p(A
198 1
66
n B)=p(A)'p(BIA) = 455 '3= 455 =0,14
26. aJ p(A
n
B)
122
= 3 .3 = 9 = 0,22
122
339
bJ p(A U B)=p(A)+p(B)-p(A n B)=-+--- =
7
=9=0,77
eJ p(A n B) = p(A)' p(B) = (1
= (1 -
- p(A))' (1 - p(B)) =
~)- (1 - ~) = %= 0,22
dJ p(A n B) =
(1 - ~). ~ = ~ = 0,44
Probabi l idad
__
30
27. p(accidente) = p(lIuvia)' p(accidente/lluvia) +
e) 100 = 0,3
+ p(sol) . p(accidente/sol) =
5
15
d}~-Ol
100 - ,
853
= -20'
. O 085 + -20'
. O 000 1 = - - = O021
40000'
(
70
e) 100 = 0,7
1 1 1 1 1 1 11
28. p(6)=-·-+_·_+-·-=-=031
3 6 3 4 3 2 36
'
29. p(deporte/fuma) =
p(deporte n fuma)
p(fuma)
=
2
30
10
31. p(al menos un doble seis en 24 tiradas) =
1
= 5' = 0,2
30
b) 120 = O6
_
Probabi
(~!
r
= 0,49
p(al menos un doble seis en 25 tiradas) =
=l-(~!r =0,51
100
30. a) - = 0 5
200
'
200
= 1-
Es ventajoso apostar doble 6 en 25 tiradas.
'
idad
y
Estadística
Evaluación (página 247)
Soluciones (Se indican con ~ lasrespuestascorrectas)
(
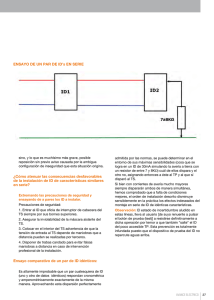
1. En un circuito se conectan tres resistencias en serie,
R1, R2 Y R3, como indica la figura:
5. En un centro de enseñanza hay 120 alumnos matriculados en primer curso. Su distribución por sexos y las
opciones escogidas figuran en la siguiente tabla de
contingencia:
OpdónA
32
26
Opdón B
37
25
Calcula la probabilidad de que un alumno seleccionado al azar:
B
•
Sea de sexo femenino:
a} 2/37
~
~ b}
0,965
e} 0,035
2. La urna A contiene 3 bolas negras y 5 blancas, y la
urna B, 4 negras y 6 blancas. Se escoge una bola de
la urna A y se introduce en la urna B. A continuación,
se extrae una bola de la urna B; ¿cuál es la probabilidad de que sea blanca?
~
a} 53/88
b} 8/11
res. El 30 % de las mujeres están casadas, y el 55 % de
los hombres, también. Si se elige al azar un empleado
y está casado, ¿cuál es la probabilidad de que sea
mujer?
a} 0,035
b} 0,965
~
~
N
vi
..;
~
a} 0,3289
b} 0,192
e} 0,024
a} 26/51
b} 25/51
e} 51/120
p(A) = 1/4;p(B) = 2/3;p(A U B) = 1/2
entonces,p(A U B) es:
a} 1/12
~
b} 7/12
e} 13/12
7. Un dado tiene una cara roja, dos amarillas y tres
verdes. Calcula la probabilidad de que:
•
Salga, como mrnimo, una cara roja o amarilla en
tres tiradas:
~
a} 0,875
b} 0,125
e} 0,176
No salga ninguna cara verde en cuatro tiradas:
•
a} 0,937 5
~ b}
0,0625
e} 0,4375
8. Determina la probabilidad de:
•
Obtener tres veces un 2 en cinco lanzamientos de
un dado:
e} 0,27
eligen 6 alumnos al azar, ¿cuál es la probabilidad de
que 4 de ellos hayan aprobado?
<-
e} 1/40
tales que:
a} 0,32
4. De un grupo de 40 alumnos hay 27 aprobados. Si se
:5
N
b} 31/40
6. Si A Y B son dos sucesos de un experimento aleatorio
e} 269/40
3. El 40% de los empleados de una empresa son muje-
a} 29/60
Curse la opción A, sabiendo que es de sexo
masculino:
•
a} 0,000 1
e} 29/40
No curse la opción B:
•
La probabilidad de que al pasar la corriente se funda
la primera resistencia es de 0,005; la de que se funda
la segunda, de 0,Q1, y la de que se funda la tercera, de
0,02. Calcula la probabilidad de que al pulsar el interruptor I se encienda la bombilla B.
~ b} 23/40
•
b} 0,023
~ e}
0,032
Obtener tres veces seguidas un 2 en cinco lanzamientos de un dado:
~
a} 0,0096
b} 0,0032
e} 0,096
oC
lO
o.
.Yl
'"~
el.
.~
~
'c'"
>
::::J
'E
~
O
g
-...
w
111
ce
~
8
e
15...
...ce
¡¡:
w
!;:
::¡¡
Probabi l idad
fa