Document

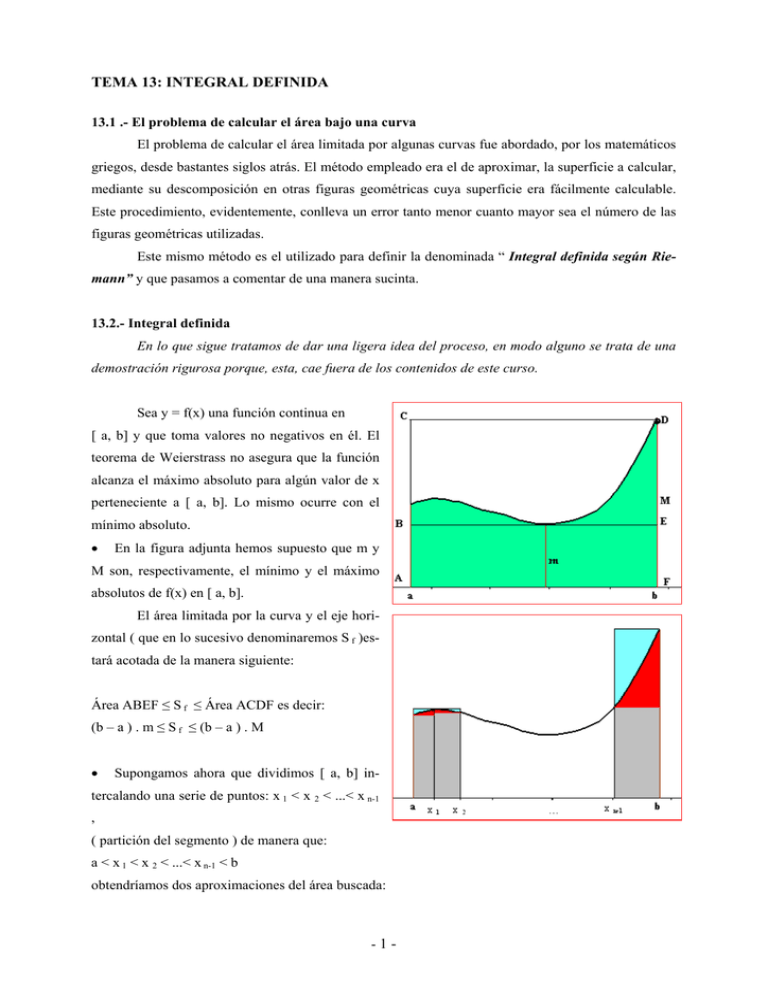
TEMA 13: INTEGRAL DEFINIDA
13.1 .- El problema de calcular el área bajo una curva
El problema de calcular el área limitada por algunas curvas fue abordado, por los matemáticos
griegos, desde bastantes siglos atrás. El método empleado era el de aproximar, la superficie a calcular,
mediante su descomposición en otras figuras geométricas cuya superficie era fácilmente calculable.
Este procedimiento, evidentemente, conlleva un error tanto menor cuanto mayor sea el número de las
figuras geométricas utilizadas.
Este mismo método es el utilizado para definir la denominada “ Integral definida según Riemann” y que pasamos a comentar de una manera sucinta.
13.2.- Integral definida
En lo que sigue tratamos de dar una ligera idea del proceso, en modo alguno se trata de una
demostración rigurosa porque, esta, cae fuera de los contenidos de este curso.
Sea y = f(x) una función continua en
[ a, b] y que toma valores no negativos en él. El
teorema de Weierstrass no asegura que la función
alcanza el máximo absoluto para algún valor de x
perteneciente a [ a, b]. Lo mismo ocurre con el
mínimo absoluto.
•
En la figura adjunta hemos supuesto que m y
M son, respectivamente, el mínimo y el máximo
absolutos de f(x) en [ a, b].
El área limitada por la curva y el eje horizontal ( que en lo sucesivo denominaremos S f )estará acotada de la manera siguiente:
Área ABEF ≤ S f ≤ Área ACDF es decir:
(b – a ) . m ≤ S f ≤ (b – a ) . M
•
Supongamos ahora que dividimos [ a, b] in-
tercalando una serie de puntos: x 1 < x 2 < ...< x n-1
,
( partición del segmento ) de manera que:
a < x 1 < x 2 < ...< x n-1 < b
obtendríamos dos aproximaciones del área buscada:
-1-
- La primera ( rectángulos de color gris )formada por una serie de rectángulos de bases : x 1 – a, x 2 – x
1, . .
. . . , b - x n-1 y alturas respectivas m 1, m 2 , ... , m n ( mínimos absolutos en cada uno de los interva-
los obtenidos en la subdivisión
El área encerrada por todos ellos será:
s 1 = (x 1 – a) . m 1 + (x 2 – x 1 ) . m 2 + . . . . . +
(b - x n-1 ) . m n
- La segunda ( rectángulos de color azul )formada
por una serie de rectángulos de las mismas bases
que en el apartado anterior y alturas respectivas M
1,
M 2 , ... , M n ( máximos absolutos en cada uno
de los intervalos obtenidos en la subdivisión
El área encerrada por todos ellos será:
S 1 = (x 1 – a) . M 1 + (x 2 – x 1 ) . M 2 + . . . . . + + (b - x n-1 ) . M n
Con las consideraciones realizadas hasta ahora tenemos que:
(b – a) . m ≤ s 1 ≤ S 1 ≤ M ( b – a )
A medida que vayamos aumentando el número de puntos de la partición de [ a, b] ( ver figura
adjunta) también aumentará el número de rectángulos obtenidos por el procedimiento señalado anteriormente. Para cada una de las particiones obtenidas iríamos obteniendo dos series de sumas que verificarían la relación:
- Para las aproximaciones por defecto ( rectángulos rojos ) s 1 ≤ s 2 ≤ s 3 ≤. .... ≤ s n
(1)
- Para las aproximaciones por exceso ( rectángulos azules ) S 1 ≥ S 2 ≥ S 3 ≥. .... ≥ S n
(2)
En resumen tenemos que en cada etapa mejoraremos ( o al menos no empeora ) las aproximaciones
del área limitada por la función f(x)
Las sucesiones obtenidas en (1) y (2) forman un par de sucesiones monótonas convergentes
porque:
La sucesión (1) es monótona creciente
La sucesión (2) es monótona decreciente
Para una división de [a, b]cualquiera se verifica que s i ≤ S i
La sucesión S 1 – s 1 , S 2 – s 2 , S 3 – s 3 ,
...,Sn
– s n es una sucesión cuyo límite es cero
La consecuencia es que las dos sucesiones tienen el mismo límite. Este límite se define como integral
definida de la función f (x) en el intervalo [a, b], y se representa en la forma
donde f(x) es la función que describe la curva, a y b son los límites de integración; a es el límite inferior, y b, el límite superior.
-2-
13.3 .- Propiedades de la Integral definida
1ª.- Si los límites de integración coinciden
∫
a
f ( x).dx = 0
a
2ª.- Si f(x) > 0 y continua en [ a, b] entonces
∫
b
3ª.- Si f(x) < 0 y continua en [ a, b] entonces
∫
b
a
a
f ( x).dx > 0
f ( x).dx < 0
4ª.- Si c es un punto interior del intervalo [ a, b], es decir, a < c < b y f(x) es continua [ a, b] entonces
∫
b
a
f ( x).dx =
5ª.6ª.-
∫
b
∫
b
c
a
f ( x).dx +
a
a
∫
f ( x).dx +
∫
b
a
∫
b
c
g ( x).dx =
c. f ( x).dx = c.
∫
b
a
f ( x).dx
∫
b
a
( f ( x) + g ( x) ).dx
f ( x).dx cualquiera que sea c
7ª.- Si para todo x € [a, b] es f(x) ≤ g(x) entonces
∫
b
a
f ( x).dx ≤
∫
b
a
g ( x).dx
8ª.- El valor de la integral definida cambia de signo si se permutan los límites de integración.
13.4 .- Teorema del valor medio de la integral
Si f(x) es continua en un intervalo cerrado [a, b], existe un punto c en el interior del intervalo
tal que:
Al valor de f( c ) se le denomina valor medio de la función f(x) en el intervalo [a,b].
-3-
Demostración
Sea f(x) una función continua en [a,b]. Hemos dicho que el área encerrada por ella, el eje OX
y las rectas x = a , x = b viene dada por:
∫
b
a
f ( x).dx
Como f(x) es continua en [a,b] alcanzará el
mínimo ( m ) y el máximo (M), absolutos,
en algún punto del citado intervalo. ( En la
figura adjunta, por sencillez, m lo alcanza en
x = b y M en x = a )
Evidentemente
Área rectángulo ABOP ≤
(b – a ) . m ≤
∫
b
a
∫
b
a
f ( x).dx ≤ área rectángulo ADRP es decir
f ( x).dx ≤ ( b – a) . M
Si dividimos a los tres miembros de la cadena de desigualdades por ( b – a ) resulta
m ≤
1
b−a
∫
b
a
f ( x).dx ≤ M
Por el teorema de los valores intermedios ( Darboux), al ser f(x) continua en [a,b], alcanzará todos los
valores intermedios entre m y M por lo que para algún x = c tendremos que
1
b−a
∫
b
a
f ( x).dx = f( c )
de donde tenemos finalmente que:
∫
b
a
f ( x).dx = ( b – a ) . f ( c )
es decir al área del rectángulo ACNP ( color rojo ) de la figura es idéntica a
∫
b
a
f ( x).dx
NOTA
Hasta ahora hemos indicado que representa
∫
b
a
f ( x).dx pero no hemos dicho cómo se calcula su va-
lor. Esto lo haremos cuando hayamos visto la Regla de Barrow. Esta es la razón por la que ahora no
proponemos ejemplos que aclaren este teorema
13.5 .- Teorema fundamental del cálculo integral
Como hemos indicado anteriormente, hasta ahora, hemos dicho que si tenemos una función
f(x), continua en [a,b], el área encerrada por ella, el eje OX y las rectas x = a , x = b viene dada por:
-4-
A=
∫
b
a
f ( x).dx
Si consideramos ahora el intervalo [a, x] ⊂ [a,b]
De igual manera podemos decir que F(X) =
∫
x
a
f (t ).dt representa el área de color, correspon-
diente al intervalo [a, x], ( superficie marcada en rojo).
Es evidente que esta superficie, F(x), dependerá de la posición que ocupe x en contraposición
de A =
∫
b
a
f ( x).dx que será un número real.
Con estas consideraciones el Teorema Fundamental del Cálculo Integral nos dice que:
“ La función F(x) que nos describe el área limitada por la curva f(x), el eje de abscisas y las recta x =
a y la abscisa variable x, es una función primitiva de la función f(x) “
F´(x) = f(x)
El teorema fundamental del cálculo nos indica que la derivación y la integración son operaciones inversas. Al integrar una función continua y luego derivarla se recupera la función original.
Ejemplos
Calcula la derivada de las funciones siguientes
1.- F(x) =
∫
x
5
e t + 1 . dt
En este caso f(t) =
e t + 1 es una función continua.
Por el T. Fundamental F´(x) =
ex +1
-5-
2.- F(x) =
∫
x
4 + t 6 . dt
0
En este caso f(t) =
4 + t 6 es una función continua.
Por el T. Fundamental F´(x) =
3.- F(x) =
∫
3
sent . dt
x
Tenemos que F(x) =
F´(x) = -
4 + x6
∫
3
sent . dt = - F(x) = -
x
∫
x
3
sent . dt
senx
4.- F(x) =
∫
x3
3
1
t 2 + 1 . dt
Por ser el límite superior x 3 necesitamos realizar un cambio de variable u = x 3
Derivando según la regla de la cadena:
dF ( x) dF ( x) d u
=
.
dx
du
dx
F´(x) =
F(x) =
x3
∫
t 2 + 1 .dt =
3
1
5.- F(x) =
∫
x2
1
∫
u
1
3
t 2 + 1 . dt.
u
du
. = ( ∫ 3 t 2 + 1 ).dt. 3 x 2 =
1
dx
3
u2 +1 . 3 x 2 =
1
. dt
1+ t2
Por ser el límite superior x 3 necesitamos realizar un cambio de variable u = x 2
Derivando según la regla de la cadena:
dF ( x) dF ( x) d u
=
.
dx
du
dx
F´(x) =
F(x) =
F´(x) =
∫
x2
1
u
du
1
1
. dt = ( ∫
. dt) .
2
2
1 1+ t
dx
1+ t
1
1
2x
.2x =
. 2x =
2
1+ u
1+ x4
1 + (x2 )2
6.- F(x) =
∫
senx
1
1
. dt
1− t2
Por ser el límite superior sen x necesitamos realizar un cambio de variable u = sen x
Derivando según la regla de la cadena:
-6-
3
x 6 + 1 .3 x 2
dF ( x) dF ( x) d u
=
.
= F´(u).u´(x)
dx
du
dx
F´(x) =
F(x) =
∫
senx
1
u
du
1
1
. dt = ∫
. dt
.
2
2
1 1− t
dx
1− t
1
1
1
. cos x =
. cos x =
2
2
cos x
1− t
1 − sen x
F´(x) =
13.6 .- Regla de Barrow
Nos dice que: si f(x) es continua en [ a, b], y G(x) es una de sus funciones primitivas, entonces:
∫
b
a
f ( x).dx = G(b) – G(a)
lo cual quiere decir que, para hallar el área limitada por la curva, el eje de abscisas y las rectas
x = a y x = b, comenzaremos buscando una primitiva cualquiera de f(x) y después hallaremos la diferencia de valores, G(b) – G(a), que toma dicha primitiva en los extremos del intervalo de integración.
13.7.- Fijando ideas
Hasta ahora habíamos dicho que el área limitada por una curva, el eje de abscisas y las rectas
x = a y x = b, la representábamos por
∫
b
a
f ( x).dx pero desconocíamos como encontrar su valor, sal-
vo en algunos casos sencillos, porque no siempre era posible calcular el límite de la sucesión de sumas
que obteníamos en la aproximación.
El Teorema fundamental nos da una pista: “ la función que describe el área, F(x), es una
primitiva de la curva que describe f(x)” pero aún así era necesario precisar más, de ahí la importancia de la Regla de Barrow que concreta, de manera precisa, cómo resolver el problema del área siempre y cuando seamos capaces de hallar G(x).
Ejemplo-1
Calcular
1
1
∫ 1+ x
0
2
. dx
La función que describe la curva es f(x) =
Una de sus funciones primitivas es G(x) =
1
1+ x2
1
∫1+ x
2
dx = arc tg x
El área buscada será pués G( 1 ) – G ( 0 ) = arc tg 1 – arc tg 0 =
-7-
π
4
Ejemplo 2 ( ejerc 63 pág 376
Ahora ya podemos proponer el siguiente ejemplo teorema del valor medio de la Integral definida
Dada la función y = x 2, halla el punto c € [ 0, 2] tal que el área
∫
2
0
x 2 dx sea igual a un rectángulo
de base 2 y altura f(c )
Solución
Área =
∫
2
0
2
x3
8
x dx =
=
3 0 3
2
Esta superficie equivale a un rectángulo 2 . f(c) de donde
2.f (c ) =
2 3
8
4
=> f (c ) =
= x 2 => x =
3
3
3
13.8.- Cálculo de áreas mediante integrales
En la figura adjunta hemos representado el área
encerrada por la función f(x) = x 3 – 2x2 – 6, el eje de abscisas y las rectas x = 1 y x = 4.
La parte marcada con ( - ) es una superficie negativa mientras que la parte marcada con (+) es positiva. Si
pretendiésemos calcular el área directamente hallando
∫
4
1
( x 3 − 2 x 2 − 6)dx cometeríamos un error porque al su-
mar las dos partes, el total, se reduciría ya que estaríamos
sumando dos cantidades de distinto signo. Para conseguir
la solución correcta debes proceder en la forma:
∫
b
•
Supongamos que queremos hallar
•
Resuelves la ecuación f(x) = 0 para hallar los puntos de corte de la curva con el eje OX. Conside-
a
f ( x)dx
remos, para fijar ideas, que las raíces son m < n.
•
Divides el intervalo de integración [a, b] en en la formas: [a, b] = [a, m] U [m, n] U [n, b]
•
Hallas una función primitiva G(x) de f(x)
•
Calculas las diferencias: |G(m) – G(a)|, | G(n) – G(m)| , | G(b) – G(n)|
•
Finalmente sumas los resultados obtenidos.
-8-
Ejemplos
1º.- Halla el área comprendida entre la función y = f(x) = x 3 – x 2 – 6x y el eje OX
Solución
Las raíces de f(x) son: - 2, 0 y 3
Primitiva de f(x) => G(x) =
3
2
∫ ( x − x − 6 x) dx =
x4 x3
- 3 x2
4
3
Cálculo de:
G(- 2) = 4 +
8
− 16
- 12 =
3
3
G(0) = 0
G(3) =
81
− 63
- 9 – 27 =
4
4
Área = | G(0) – G(-2)| + |G(3) – G(0)| =
|0 +
16
− 63
153
|+|
- 0| =
3
4
12
A la derecha se muestra la representación
gráfica del ejercicio
2º.- Calcula el área comprendida entre la curva f(x) = 3 x 2 – x + 1, el eje X y las rectas x = 0 y
x=4
Solución
Las raíces de f(x) son: No tiene
Primitiva de f(x) =
∫ (3x
2
− x + 1) dx = x 3 -
x2
+x
2
Cálculo de:
G( 0 ) = 0
G( 4 ) = 64 – 8 + 4 = 60
Área = | 60 - 0| = 60
La superficie pedida aparece de color verde en
la figura de la derecha
13.9.- Área comprendida entre dos curvas
El área entre las gráficas de y=f(x) , y=g(x) en el intervalo [a,b]
está dado por el valor de la Integral Definida de |f-g| en [a,b].
Consideraremos los casos siguientes:
a) Que f(x) y g(x) no se cortan ( figura adjunta)
-9-
El área será la diferencia de las encerradas, por cada una de las curvas, el eje de abscisas y las rectas
x = a y x = b ( superficie coloreada).
A=
∫
b
a
f ( x)dx -
∫
b
a
g ( x)dx
Que por las propiedades de la integral definida equivale a: A =
∫
b
a
( f − g )( x) dx
Es decir obtengamos la función diferencia ( f – g ) y obtengamos el área encerrada por esta curva entre
los límites x = a, x = b y el eje de abscisas.
Ejemplo
Hallar el área encerrada por la curva
y = x 2 – 2x + 1, la recta y = 1 y las rectas x =
3 y x = 5 ( superficie coloreada)
Función f – g = (x 2 – 2x + 1) – ( 1 ) = x 2 – 2x
A=
5
5
3
3
∫ ( f − g )( x) dx = ∫ ( x
2
− 2 x) dx =
x3
- x2
3
A(5) =
50
3
A(3) = 0
Área =
50
50
-0=
3
3
b) Que f(x) y g(x) se corten en dos puntos
⎧ y = f ( x)
que equivale a encontrar las
⎩ y = g ( x)
Para encontrar los puntos de corte se resuelve el sistema ⎨
soluciones de la ecuación f(x) – g(x) = 0
Las raíces de esta ecuación serán los límites de
integración, procediendo, acto seguido, como en el
apartado anterior.
Ejemplo .- Halla el área limitada por la curva
y = - x 2 + 3 x +4 y la recta y = 2x + 2
La función f(x) – g(x) = - x 2 + x +2
tiene como raíces x = - 1 y x = 2
el área pedida es pues
∫
2
−1
( f − g )( x)dx =
∫
2
−1
(− x 2 + x + 2)dx
- 10 -
Una primitiva es A(x) =
2
∫ (− x + x + 2)dx = -
A(2) = -
8
10
+2+4=
3
3
A(- 1) =
1 1
7
+
-2=3 2
6
Área A(2) – A( - 1) =
x3
x2
+
+ 2x
3
2
27
6
c) Que f(x) y g(x) se corten en más de dos puntos
En este caso, igual que en el apartado anterior, se buscan las raíces de la ecuación
f(x) – g(x) = 0.
Supongamos, para fijar ideas, que estas son m, n y p tales que:
a<m<n<p<b
Descomponemos el intervalo de integración [a, b] como unión de los subintervalos [a, m],
[m, n], [n, p] y [p, b] para después calcular el área en cada uno de ellos y tomar el valor absoluto de
la cantidad hallada.
El área total será la suma de las áreas parciales encontradas.
Ejemplo
Ejercicio: 5-d) libro texto pág 373
⎧ y = x( x − 1)( x − 2)
⎩y = 0
Calcula el área comprendida entre las curvas ⎨
Solución
Las raíces de la función f(x) – g(x) = x ( x – 1) ( x – 2) – 0 = x ( x – 1) ( x – 2) son: x = 0, x = 1 y x = 2
El área pedida es A02 = | A02 | + | A02 |
Buscamos una función primitiva, que será la misma para los dos sumandos.
A(x) =
∫
x4
( x – 3 x + 2 x) dx =
- x3 + x2
4
3
2
A(0) = 0
A(1) =
1
4
A(2) = 0
A02 = | A02 | + | A02 | = | A(1) – A(0) | + | A(2) – A(1) | =
- 11 -
1
1
1
+||=
4
4
2
La figura anterior es la representación gráfica del ejercicio. La función y = x ( x – 1) ( x – 2) está dibujada en color rojo mientras que y = 0 ( eje de abscisas) aparece en color negro
13.10.- Volumen de un cuerpo de revolución
Supongamos que a la gráfica de f(x) se la hace girar alrededor del eje OX. La figura obtenida
tiene un volumen que viene dado por:
V=
∫ [ f ( x)] .π .dx
b
2
a
Ejemplo
Se considera la circunferencia x 2 + y 2 = 25. Hallar el volumen de la esfera que se obtiene al girar
alrededor de uno de sus diámetros dicha circunferencia.
Solución
La función de giro es: f(x) =
25 − x 2
Límites de integración: 25 – x 2 = 0 => x = -5 y x = 5
Volumen
∫
5
−5
[ 25 − x ] .π .dx = ∫
2
2
5
−5
π (25 − x 2 ).dx
•
Función primitiva V(x) = π ( 25x -
•
V(5) = 125 -
•
V(- 5) = - 125 +
Volumen = π (
x3
)
3
125 250
=
3
3
125
250
=3
3
250
250
500
-())=π
3
3
3
- 12 -
Ejercicios
1º.- (ejerc 16 pág 373) Halla el área limitada por la función y = 2 x – x 2 y sus tangentes en los
puntos en los que corta al eje de abscisas.
Solución
•
Puntos de corte con el eje de abscisas 2 x – x 2 = 0 => x = 0 y x = 2
•
Rectas tangentes
y´= 2 – 2x => y´(0) = 2
e y´(2) = - 2
y = 2 x e y = - 2 ( x – 2 ) => y = - 2 x + 4
El área pedida aparece coloreada en la figura
Necesitamos hallar la abscisa de intersección de
ambas rectas tangentes
⎧ y = 2x
=> x = 1
⎨
⎩ y = −2 x + 4
Área azul
Función diferencia (2 x – x 2 ) – 2x = - x 2
x3
1
=> Área = A(1) – A(0) =
Área = ∫ − x .dx = > A(x) = 0
3
3
1
2
Área amarilla
Función diferencia (2 x – x 2 ) – ( - 2x + 4) = - x 2 + 4 x - 4
Área =
∫
2
1
(− x 2 + 4 x − 4).dx = >A(x) = -
Área total =
x3
− 20 − 1
13
+ 2 x – 4 x => Área = A(2) –A(1) =
-(
)=
3
3
3
3
1 13 14
+
=
3 3
3
- 13 -