TEMA 9: INTEGRALES. CÁLCULO DE ÁREAS
Anuncio
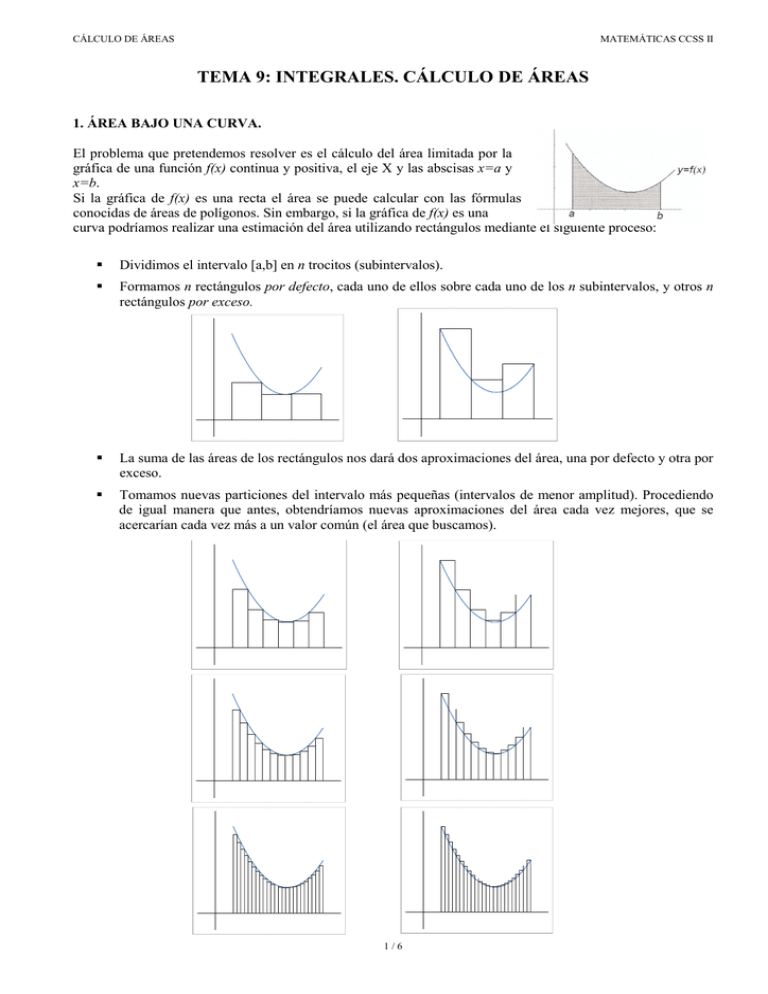
CÁLCULO DE ÁREAS MATEMÁTICAS CCSS II TEMA 9: INTEGRALES. CÁLCULO DE ÁREAS 1. ÁREA BAJO UNA CURVA. El problema que pretendemos resolver es el cálculo del área limitada por la gráfica de una función f(x) continua y positiva, el eje X y las abscisas x=a y x=b. Si la gráfica de f(x) es una recta el área se puede calcular con las fórmulas conocidas de áreas de polígonos. Sin embargo, si la gráfica de f(x) es una curva podríamos realizar una estimación del área utilizando rectángulos mediante el siguiente proceso: Dividimos el intervalo [a,b] en n trocitos (subintervalos). Formamos n rectángulos por defecto, cada uno de ellos sobre cada uno de los n subintervalos, y otros n rectángulos por exceso. La suma de las áreas de los rectángulos nos dará dos aproximaciones del área, una por defecto y otra por exceso. Tomamos nuevas particiones del intervalo más pequeñas (intervalos de menor amplitud). Procediendo de igual manera que antes, obtendríamos nuevas aproximaciones del área cada vez mejores, que se acercarían cada vez más a un valor común (el área que buscamos). 1/6 CÁLCULO DE ÁREAS MATEMÁTICAS CCSS II Se forman así dos sucesiones de áreas una por defecto y otra por exceso. El límite, cuando el número de puntos de la partición tiende a +∞ (o, lo que es lo mismo, cuando las amplitudes de los subintervalos tienden a 0), de ambas sucesiones coincide y es el área buscada. Si f(x) es una función continua en el intervalo [a,b] definimos la integral definida de la función en el intervalo [a,b] como el límite de las áreas por defecto y por exceso definidas anteriormente. Se representa: b ∫a f ( x)dx . En vez de rectángulos, pueden utilizarse trapecios, con los que se consigue una convergencia más rápida. Como es fácil de comprender, el método que acabamos de describir es muy engorroso a poco que la función f(x) se complique. En el siglo XVII, Isaac Barrow puso en conexión los conceptos de derivada e integral, al darse cuenta de que la derivada de la función que proporciona el área bajo una curva es la función misma que representa dicha curva. Por lo que el problema se reducía a buscar esa función “primitiva” que, al derivarla, nos diera la función que representa la curva. 2. PRIMITIVA DE UNA FUNCIÓN. El cálculo de la primitiva de una función es el proceso contrario al de derivación. Si derivamos la función f ( x) = x3 tenemos f ′( x) = 3 x 2 . Si presentamos la situación al revés y partimos de y = 3 x 2 diremos que x3 es una primitiva de 3x 2 . “Decimos que F(x) es una primitiva de f(x) si F ′( x) = f ( x) ” Nos planteamos el problema inverso al de obtener la derivada de una función: dada una función f(x), debemos encontrar una función F(x) cuya derivada sea f(x). Ejemplos: 1. Si f ( x) = cos x → F ( x) = senx , ya que F ′( x) = cos x 2. Si f ( x) = 2 x → F ( x) = x 2 , ya que F ′( x) = 2 x 1 2x 1 e , ya que F ′( x) = ⋅ e2 x ⋅ 2 = e 2 x 2 2 1 1 4. Si f ( x) = x → F ( x) = x 2 , ya que F ′( x) = ⋅ x ⋅ 2 = x 2 2 3. Si f ( x) = e 2 x → F ( x) = 2/6 CÁLCULO DE ÁREAS MATEMÁTICAS CCSS II También podría ser una primitiva de y = 3 x 2 cualquiera de las funciones x3 , x3 + 1, x3 + 8, x3 − 7 , .... , por eso en general si F(x) es una primitiva de f(x), también son primitivas de f(x) todas las funciones de la forma F(x)+C, siendo C ∈ R . 3. INTEGRAL INDEFINIDA. Llamaremos integral indefinida de f(x) al conjunto formado por todas las primitivas de la función f(x). Lo representaremos: f ( x) dx . ∫ Si F(x) es una primitiva cualquiera de f(x), la integral indefinida de f(x) es : ∫ f ( x)dx = F ( x) + C La constante C se denomina constante de integración. La función que se desea integrar, f(x), se llama integrando. La diferencial de x, dx, indica la variable respecto de la cual se integra. Notar que sin dx no se podría contestar a integrales como 2 = ? ; el resultado puede ser 2x, 2y, 2t,….según ∫ sea la variable que consideremos. ∫ 2dx = 2 x + C , ∫ 2dy = 2 y + C , o bien ∫ 2dt = 2t + C Integración f ( x) = 3x 2 F ( x) = x 3 Derivación 4. PROPIEDADES DE LA INTEGRAL INDEFINIDA. Son consecuencia directa de la propia definición de integral y de las reglas de derivación: 1. ∫ [ f ( x) + g ( x)] dx = ∫ f ( x)dx + ∫ g ( x)dx Ejemplo: 1 1 ∫ 2 x + x + cos x dx = ∫ 2 xdx + ∫ x dx + ∫ cos xdx = x = x 2 + ln x + senx + C 2. ∫ k ⋅ f ( x)dx = k ⋅ ∫ f ( x)dx Ejemplo: ∫ 3e dx = 3∫ e dx =3e x x x +C 3/6 2 + C1 + ln x + C2 + senx + C3 = CÁLCULO DE ÁREAS MATEMÁTICAS CCSS II 5. INTEGRALES INMEDIATAS. Por aplicación directa de las reglas de derivación se obtiene la siguiente tabla de integrales inmediatas: Funciones elementales F. identidad: F. potencial: ( n ≠ −1 )* Función compuesta ∫ dx = x + C n ∫ x dx = x n +1 +C n +1 ∫ f ( x)n ⋅ f ′( x) ⋅ dx = f ( x) n +1 +C n +1 1 1 * n = −1 ∫ x dx = ln x + C → ∫ f ( x) ⋅ f ′( x) ⋅ dx = ln F. exponencial: ∫ e dx = e ∫e Funciones trigonométricas: ∫ senxdx = − cos x + C ∫ f ′( x) ⋅ s en( f ( x))dx = − cos( f ( x)) + C ∫ cos xdx = senx + C ∫ f ′( x) ⋅ co s( f ( x))dx = s en( f ( x)) + C x x +C f (x) f ( x) + C ⋅ f ′( x)dx =e f ( x ) + C x n +1 +C . La regla de integración más importante que necesitamos es la de la potencia: ∫ x dx = n +1 n Utilizada junto con las propiedades 1 y 2 nos permite integrar (calcular la primitiva) de cualquier polinomio: Ejemplos: 1. 2 2 2 ∫ (5 x + x + 4)dx = ∫ 5x dx + ∫ xdx + ∫ 4dx = 5∫ x dx + ∫ xdx + 4∫ dx = 5 = 2. x3 x2 + + 4x + C = 3 2 5 x3 x 2 + + 4x + C 3 2 2 ∫ (3x + x + 4) dx = 3 x3 x 2 x2 + + 4 x + C = x3 + + 4 x + C 3 2 2 6. REGLA DE BARROW. Si f(x) es una función continua en [a,b], la integral definida de f(x) es ∫a f (x ) dx = F (b ) − F (a ) b siendo F(x) una función que cumpla F ′( x) = f ( x) , es decir, la función F(x) es una primitiva cualquiera de f(x). Si, además, f(x) es positiva en [a,b], la integral definida anterior da un resultado positivo que coincide con el área encerrada entre la gráfica de la función, el eje X y las rectas x=a y x=b. 4/6 CÁLCULO DE ÁREAS MATEMÁTICAS CCSS II Si f ( x) ≥ 0 en [a,b] b A = ∫ f ( x)dx + a En cambio, si f(x) es negativa en [a,b], la integral definida anterior nos da un resultado negativo, pero que es igual en valor absoluto al valor del área buscada. Si f ( x) ≤ 0 en [a,b] ∫ – b a f ( x)dx = − A En consecuencia, el valor absoluto de la integral definida nos dará el valor del área en ambos casos: A= ∫ b a f ( x)dx Si f(x) cambia de signo en [a,b], hemos de calcular por separado la integral de cada una de las zonas y sumar sus valores absolutos. Para ello hemos de hallar, en primer lugar, los puntos de corte de la función f(x) con el eje X (solamente tomaremos en consideración aquellos puntos de corte que se encuentren entre a y b). A= ∫ c a f ( x)dx + ∫ b c f ( x)dx Un procedimiento similar a este hemos de utilizar cuando integremos una función definida “a trozos”. Luego, no siempre la integral coincide con el área que deseamos calcular, sólo cuando f ( x) ≥ 0 . Ejemplos: 1) Área limitada por f ( x) = x 2 y el eje X desde x=1 hasta x=4: 4 ∫ 4 1 x3 43 13 64 1 x dx = + C = + C − + C = + C − − C = 21u 2 3 3 1 3 3 3 2 2) Calcula ∫ 4 0 x2 + 1 0 ≤ x < 2 f ( x)dx , f ( x) = : − x + 7 2 ≤ x ≤ 4 2 4 x3 − x2 f ( x ) dx = ( x + 1) dx + ( − x + 7) dx = + x + 7 x = + ∫0 ∫0 ∫2 3 0 2 2 8 38 −16 −4 14 = + 2 − 0 + + 28 − + 14 = + [ 20 − 12] = 3 2 2 3 3 4 2 2 4 5/6 CÁLCULO DE ÁREAS MATEMÁTICAS CCSS II Ejercicios: 1. Calcula el área comprendida por la curva de ecuación f(x)=x2+2, el eje OX y las rectas x=1 y x=4. 2. Halla el área de la superficie encerrada por la función f ( x) = − x 2 + x + 2 y el eje OX. 3. Calcula el área comprendida entre la curva de ecuación f(x)=x3 y las rectas x = 0 y x = 2 . ¿Qué ocurre si es de x = −2 hasta x = −1 ? ¿Y si es de x = −1 hasta x = 2 ? 4. Calcula el área de la siguiente figura, siendo la parábola y=x2 y la altura horizontal 16 5. Una chapa de plata tiene la forma y dimensiones que se indican en el dibujo, y la curva que la delimita superiormente es la parábola de ecuación y = 4 − x 2 . Determina el área de la chapa. 0≤ x<2 x+2 2 6. Dada la función: f ( x) = x − 6 x + 12 2 ≤ x < 4 −2 x + a 4< x≤8 a) Halla el valor de a para que la función y= f(x) sea continua en el intervalo [0,8]. b) Halla los máximos y mínimos absolutos de y= f(x) en el intervalo [0,4]. Justifica que los puntos encontrados son máximos y mínimos absolutos. c) Calcula el área de la región del plano limitada por las rectas de ecuación y=0 , x=0 , x=3 y la gráfica de y=f(x). − x 2 − 2 x + 3 si 0 ≤ x < 1 7. Dada la función f ( x ) = si 1 ≤ x ≤ 3 x −1 Estudia la continuidad de la función en el intervalo [0,3]. Calcula los máximos y mínimos absolutos de f(x). c) Calcula el área de la región determinada por la gráfica de la función y las rectas x=0 , y=0 y x=3. a) b) 6/6