02 Capitulo 2

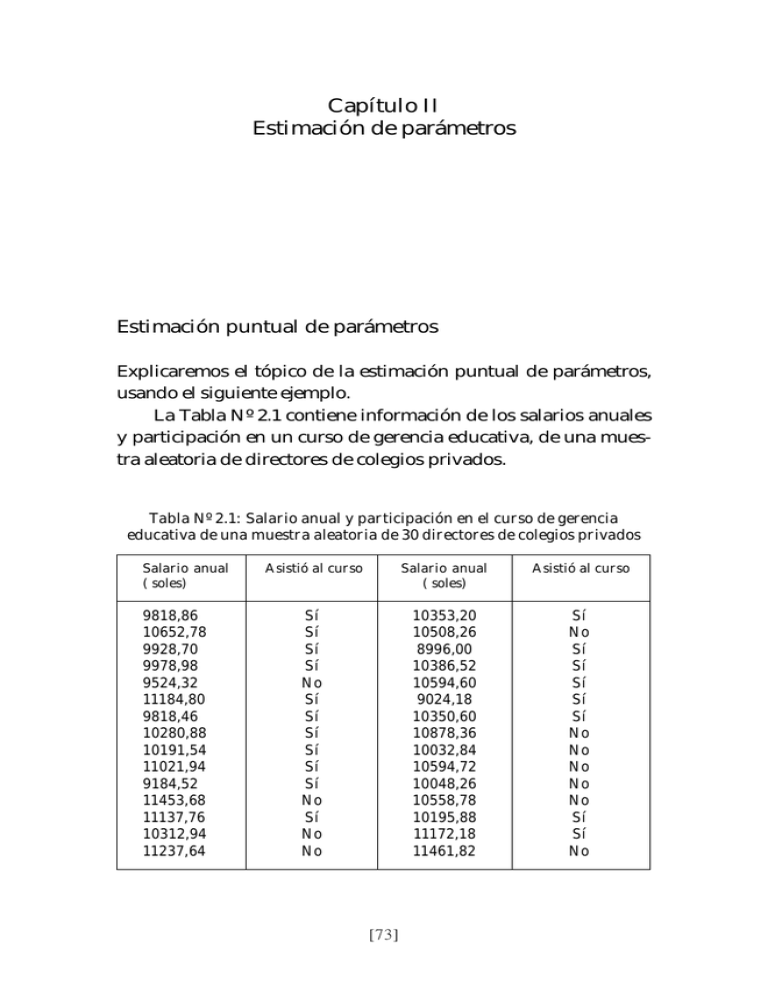
Capítulo II
Estimación de parámetros
Estimación puntual de parámetros
Explicaremos el tópico de la estimación puntual de parámetros,
usando el siguiente ejemplo.
La Tabla Nº 2.1 contiene información de los salarios anuales
y participación en un curso de gerencia educativa, de una muestra aleatoria de directores de colegios privados.
Tabla Nº 2.1: Salario anual y participación en el curso de gerencia
educativa de una muestra aleatoria de 30 directores de colegios privados
Salario anual
( soles)
9818,86
10652,78
9928,70
9978,98
9524,32
11184,80
9818,46
10280,88
10191,54
11021,94
9184,52
11453,68
11137,76
10312,94
11237,64
Asistió al curso
Salario anual
( soles)
Asistió al curso
Sí
Sí
Sí
Sí
No
Sí
Sí
Sí
Sí
Sí
Sí
No
Sí
No
No
10353,20
10508,26
8996,00
10386,52
10594,60
9024,18
10350,60
10878,36
10032,84
10594,72
10048,26
10558,78
10195,88
11172,18
11461,82
Sí
No
Sí
Sí
Sí
Sí
Sí
No
No
No
No
No
Sí
Sí
No
[73]
71
Se utiliza la notación x1 , x2 , etc., para indicar el salario anual
del primer director, del segundo, y así sucesivamente.
Por ejemplo, para estimar µ, la media de la población del salario anual de los directores y, σ, la desviación estándar del salario anual de los directores, se toman los datos de la Tabla Nº 2.1
para calcular los valores de los correspondientes estadísticos: la
media de la muestra X y la desviación estándar de la muestra S.
Así, tenemos que en la muestra observada, la media del salario
anual de los directores es:
∑x
310884
i
=
= 10362.80 ,
n
30
y la desviación estándar:
x=
s=
∑ (x − x ) =
i
n −1
448288.6381
= 669.54
29
Por otro lado, si en dicha muestra se calcula la proporción de
los directores que asistieron al curso de gerencia educativa, podemos estimar la proporción de directores en la población, π, que
terminaron el curso de gerencia educativa. La tabla Nº 2.1 indica
que 19 de los 30 directores de la muestra terminaron el curso, entonces la proporción en la muestra, representada por p, es:
19
= 0,63 ; que se usa para estimar el parámetro π de la
30
población.
p=
Al hacer los cálculos anteriores hemos efectuado el procedimiento estadístico denominado estimación puntual. Usamos los
datos de la muestra para calcular un valor de un estadístico de la
muestra que sirva como estimación de un parámetro de la población.
En la notación de la estimación puntual, se dice que X es el
estimador puntual de la media poblacional µ, S es el estimador
puntual de la desviación estándar poblacional σ, y que P es el estimador puntual de la proporción π poblacional. A los valores nu-
72
méricos de X , S o P, obtenidos en una determinada muestra se
les llaman estimaciones puntuales del parámetro y los hemos denotado con: X , s, p.
A continuación y para cualquier otro caso se resume la notación:
Parámetros
µ: Promedio o media
poblacional
Estimadores
(Funciones)
Estimación
X : Promedio o media
muestral
Valor numérico
obtenido para X
x=
π: Proporción poblacional
P: Proporción muestral
∑x
i
n
p: valor numérico de
la proporción muestra
∑ (x − x )
2
σ: Desviación estándar
poblacional
S: Desviación
estándar muestral
s=
i
n −1
valor de la desviación
estándar
X 1 , X 2 , … X n , es una muestra aleatoria desde la población
donde la variable aleatoria X tiene esperanza E (X ) = µ , y varianza σ 2 = E (X − µ )2 ; x1 , x2 , …, xn son valores observados de la
muestra aleatoria.
Así, para la muestra de 30 directores, la estimación puntual
de µ es de x = 10362.80 soles, la de σ es de 669.54 soles y la de P
es 0.63. La Tabla Nº 2.2 contiene un resumen de los resultados de
la muestra y compara las estimaciones puntuales con los valores
reales de los parámetros de la población.
Como se observa a continuación, ninguna de las estimaciones puntuales son exactamente iguales a los parámetros poblacionales correspondientes. Se esperaba esta variación porque se está
usando sólo una muestra y no la información de toda la población
para obtener la estimación.
73
Tabla Nº 2.2: Resumen de estimaciones puntuales obtenidas a partir de una
muestra Aleatoria simple de 30 directores de colegios
Parámetro de la
población
puntual
Valor del parámetro
µ: Promedio poblacional
Estimador
(en soles)
Estimación
puntual
11 000
X : Promedio
muestral del
salario anual
x = 10 362.8
σ: Desviación estándar
700
S: Desviación
estándar muestral
del salario anual
s = 669.54
π: Proporción poblacional
0.60
P: Proporción muestral
p = 0.63
del salario anual
poblacional del salario
anual
de directores que
terminaron el curso
de directores que
terminaron el curso
Error de muestreo. El valor absoluto de la diferencia entre
estimador insesgado y el parámetro poblacional correspondiente
se llama error de muestreo. Para la media muestral, la desviación
estándar y la proporción muestral, los errores de muestreo son
X − µ , S − σ y P − π , respectivamente. Por tanto, para la muestra de directores de colegios, los errores de muestreo son
x − µ = 10362.80 − 11000 = 637.20 soles, s − σ = 669.5 − 700 = 30.46
soles para la desviación estándar muestral y
P − π = 0.63 − 0.60 = 0.03 para la proporción muestral.
En este caso pudimos calcular los errores de muestreo porque hemos supuesto que conocemos los parámetros poblacionales. Sin embargo, en una aplicación real de muestreo no podemos
calcular de manera exacta el error de muestreo, porque no se conoce el valor del parámetro poblacional.
Propiedades de los estimadores puntuales
En la sección anterior hemos mostrado cómo se pueden usar las
estadísticas o estimadores: la media de la muestra X , la desviación estándar muestral S y la proporción muestral P como estima-
74
dores puntuales de sus correspondientes parámetros poblacionales, µ , σ y π . Resulta intuitivamente atractivo que cada uno de
esos estadísticos de muestra sea estimador puntual de su parámetro poblacional correspondiente. Sin embargo, antes de emplear
algún estadístico de muestra como estimador puntual, se debe
comprobar si tiene ciertas propiedades asociadas con los buenos
estimadores puntuales. En esta sección describiremos de manera
sucinta algunas propiedades de los buenos estimadores puntuales: insesgamiento, eficiencia y consistencia.
En vista que se pueden emplear diversas estadísticas como
estimadores puntuales de distintos parámetros poblacionales, en
esta sección usaremos la siguiente notación general:
θ : parámetro poblacional de interés
θˆ : estadístico de muestra o estimador puntual de θ .
La notación θ es la letra griega theta, y la notación θˆ se llama
"theta sombrero". En general, θ representa cualquier parámetro
de la población, como por ejemplo la media poblacional, la desviación estándar poblacional, la proporción poblacional, etc., θˆ
representa la estadística o estimador correspondiente, como la
media muestral, la desviación estándar muestral y la proporción
muestral.
Estimador insesgado
Si el valor esperado de la estadística es igual al parámetro poblacional que se estima, se dice que esa estadística es un estimador
insesgado del parámetro poblacional.
La estadística θˆ es un estimador insesgado del parámetro
poblacional θ , si:
()
()
E θˆ = θ ,
donde E θˆ es el valor esperado de la estadística θˆ .
Al describir las distribuciones muestrales de la media y la
proporción muestrales, dijimos que E X = µ y E (P ) = π . Enton-
( )
75
X como P son estimadores insesgados de sus parámetros poblacionales correspondientes, µ y π . También se pue-
ces, tanto
( )
2
2
de desmostrar que E S = σ , es decir, S 2 es un estimador inses-
gado de la varianza poblacional σ 2 , donde S 2 =
∑ Xi .
X =
n
∑ (X
i
−X
n −1
)
2
y
Estimador eficiente
Suponga que en una muestra aleatoria simple de n elementos se
tiene dos estimadores puntuales insesgados, θˆ1 y θˆ2 del mismo
parámetro poblacional θ , entonces, preferiremos usar el estimador puntual con la menor desviación estándar, porque tiende
a proporcionar una estimación más cercanas al parámetro poblacional.
() ( )
()
( )
Si E θˆ1 = E θˆ2 = θ y Var θˆ1 < Var θˆ2 → θˆ1 es más eficiente que θˆ2 . Se dice que θˆ1 es un estimador puntual insesgado
con menor desviación estándar y tiene mayor eficiencia relativa
que el estimador θˆ2 .
Estimador consistente
Una tercera propiedad asociada con los buenos estimadores puntuales es la consistencia. Hablando en términos generales, un estimador puntual es consistente si sus valores tienden a acercarse al
parámetro de la población conforme se incrementa el tamaño de
la muestra. En otras palabras, un tamaño de muestra grande tiende a proporcionar un mejor estimador puntual que un tamaño
pequeño. Observe que en el capítulo anterior se vio que la desviación estándar de la media muestral X , fue σ X =
σ
. Como σ X
n
se relaciona con el tamaño de la muestra, de tal manera que las
76
muestras mayores dan menores valores de σ X , llegamos a la conclusión que un tamaño de muestra mayor tiende a producir estimaciones puntuales más cercanas a la media de la población µ. En
este sentido, se dice que la media muestral, X , es un estimador
consistente de la media poblacional µ. Con el mismo razonamiento podemos llegar a la conclusión que la proporción muestral P es
un estimador consistente de la proporción poblacional π y S es un
estimador consistente de σ.
Estimación por intervalos en poblacones normales
Introducción
Aunque X es un buen estimador puntual de µ, es obvio señalar
que hay una discrepancia (error) entre X y µ,; entonces para confiar en X como estimador de µ, se debe conocer el error e = X − µ
y el riesgo de error; vale decir hay que encontrar la precisión del
estimador.
En este caso, la explicación para los estimadores se refiere a
los estimadores puntuales y el concepto se denomina estimación
puntual; es decir, dado un parámetro, por ejemplo µ, se estima
con un valor de X , x . Una deficiencia de los estimadores puntuales es que no están vinculados a un juicio de probabilidad y que no
se puede establecer la probabilidad que hay de que X sea igual a µ.
Otra manera de estimar µ, es que éste se encuentre entre dos
valores a y b, a lo que se llama estimación por intervalo.
Por ejemplo, se dirá que la calificación media de las notas del
curso de estadística está entre 15 y 18 puntos, de modo que
15 ≤ µ ≤ 18 .
La estimación por intervalos consiste en atribuir al parámetro que se desee estimar no un valor concreto sino un rango de
valores entre los que se espera que puede encontrarse el verdadero valor del parámetro con una probabilidad alta y conocida.
El rango de valores entre los cuales con determinada probabilidad se encuentra el parámetro, se denomina intervalo confi-
77
dencial y tiene por limites confidenciales a los valores LI (Límite
Inferior) y LS (Límite Superior).
Se llama nivel de confianza (1 − α ) a la probabilidad que el
intervalo construido incluya el verdadero valor del parámetro, por
ejemplo a µ.
Para construir intervalos de confianza, necesitamos saber la
distribución teórica de la estadística utilizada como estimador.
Conocida esta distribución podemos conocer la probabilidad asociada a cada uno de sus valores.
A continuación presentaremos la metodología para encontrar
los intervalos de confianza para algunos parámetros.
Intervalos de confianza para la media con varianza conocida
Consideremos una población con distribución normal donde está
definida una variable aleatoria X con media desconocida µ y varianza σ 2 conocida, cuya notación es N (0,1). Encontraremos un
intervalo de confianza para la media poblacional µ.
En el capítulo anterior hemos visto, que para una muestra aleatoria, X 1 ,..., X n , tomada de la población anterior, la variable aleatoria media muestra, X , se distribuye normalmente con media µ
y varianza
X −µ
σ2
. Por tanto, la variable estandarizada Z =
se
σ
/ n
n
distribuye N (0,1).
Para α > 0, es posible hallar el percentil z −α de la distribu(1
)
2
ción normal, para el cual:
P(− z(1−α / 2 ) ≤ Z ≤ z(1−α / 2 ) ) = 1 − α . Luego se tiene que:
− z(1−α / 2 ) ≤
X −µ
≤ z(1−α / 2 ) .
σ/ n
Así, el intervalo para µ con un nivel de confianza (1 − α ) es:
X − z(1−α / 2 )
78
σ
σ
≤ µ ≤ X + z(1−α / 2 )
.
n
n
Luego, un intervalo de confianza al nivel (1 − α ) , para la
media poblacional µ, cuando ya se observó la muestra de tamaño n es:
α
2
α
2
z(1−α
x − z(1−α / 2 )
2
)
z(1−α
2
)
σ
σ
≤ µ ≤ x + z1−(α / 2 )
,
n
n
(2.1)
Por ejemplo, al nivel de confianza del 95% ( α = 0,05 ), un intervalo de confianza para µ es:
x − 1.96
σ
σ
≤ µ ≤ x + 1.96
.
n
n
Al nivel de confianza del 99% ( α = 0,01 ), el intervalo de confianza para µ es:
x − 2.58
σ
σ
≤ µ ≤ x + 2.58
n
n
Observemos que cuando se observa la muestra los estimadores se reemplazan por las respectivas estimaciones.
Ejemplo 2.1
Una muestra aleatoria de 100 estudiantes de Administración Educativa respondió a una prueba de inteligencia espacial. En esa
muestra se obtuvo una media de 80 puntos y se conoció que en la
población la desviación típica era 1 punto. Obtendremos un intervalo de confianza para hallar la verdadera inteligencia espacial
79
media de los estudiantes de Administración Educativa, con un
nivel de confianza de 0.99.
Solución
Para α = 0.01 , en la tabla normal se obtiene z(1−α / 2 ) = zteórico = 2.58.
Se sabe que σ = 1 y x = 80 .
Reemplazando en (2.1) tenemos:
x − 2.58
σ
σ
≤ µ ≤ x + 2.58
n
n
(1)
80 − 2.58
100
≤ µ ≤ 80 + 2.58
(1)
100
80 − 0.258 ≤ µ ≤ 80 + 0.258
79.74 ≤ µ ≤ 80.26
Luego, la verdadera inteligencia espacial media de los estudiantes de Administración Educativa se encontrará entre 79.74 y
80.26, con un nivel de confianza del 99%.
Intervalo de confianza para la media poblacional cuando la varianza es
desconocida(muestras pequeñas)
En poblaciones normales con varianza desconocida, el intervalo
para estimar µ , al nivel de confianza de (1 − α ) , es:
X − t(1−α / 2 )
S
S
≤ µ ≤ X + t(1−α / 2 )
,
n
n
donde: t(1−α / 2 ) = tteórico es la abscisa de la distribución t-Student con
n − 1 grados de libertad, P[t(n −1) < t(1−α / 2 ) ] = 1 −
Ejemplo 2.2
80
α
y
2 S=
∑ (X
i
−X
n −1
)
2
.
Una muestra aleatoria de 20 estudiantes de la Facultad de Educación responden a una prueba de inteligencia espacial, obteniéndose una media de 70 y una desviación típica de 1 ¿Entre qué límites se hallará la verdadera inteligencia espacial media de los
estudiantes de Educación, con un nivel de confianza 0.95?. Suponga
que los puntajes medios de la prueba de inteligencia espacial se
distribuyen normalmente.
Solución
Si α / 2 = 0.025 en la tabla t-Student se encuentra: t(1−α / 2 ) = tteórico =
t( 0.975,19 ) = 2.091 y en la muestra observada se tiene: s = 1 x = 70 .
Luego, un intervalo de confianza del 95% para µ es:
x − t(1−α / 2 )
70 − 2.091
s
s
≤ µ ≤ x + t(1−α / 2 )
n
n
(2.2)
1
1
≤ µ ≤ 70 + 2.091
20
20
70 − 0.4676 ≤ µ ≤ 70 + 0.4676
69.53 ≤ µ ≤ 70.47
Luego, la verdadera inteligencia espacial media de los estudiantes de Educación se encuentra entre 69.53 y 70.47, con un nivel de confianza del 95%.
Intervalos de confianza para la media con varianza
desconocida en muestras grandes (cualquier distribución)
Cuando el tamaño de muestra que se toma es suficientemente grande (mayor que 30), aún cuando no se conozca la distribución de la
variable X , por el teorema del límite central:
Z=
X −µ
σ
n
y
t =
X −µ
S
n
81
tienen distribución aproximadamente normal y pueden usarse
para construir los intervalos de confianza referentes a la media
poblacional.
El intervalo de confianza al nivel (1 − α ) para la media poblacional µ, con σ desconocido y en muestras grandes es:
X − z(1−α / 2 )
S
S
≤ µ ≤ X + z(1−α / 2 )
.
n
n
Ejemplo 2.3
Para estimar el promedio de los salarios docentes de una universidad, se tomó una muestra aleatoria de 50 docentes, donde se
encontró que la media de los sueldos es 840.1 soles y la varianza
es 122.44 (soles)2.
Obtendremos un intervalo de confianza del 95% para estimar la media de los salarios de todos los docentes de esa universidad.
Solución
x = 840.1 soles,
n = 50
s = 122.44 = 11.07 soles.
A pesar que no se conoce la distribución poblacional de los
salarios, como la muestra es grande nos basamos en el teorema
del límite central. Así, para α = 0.05 el valor de z(1−α / 2 ) = 1.96.
Luego, un intervalo para µ, al nivel de confianza del 95% es:
x − z(1−α / 2 )
840.1 − 1.96
s
s
≤ µ ≤ x + z(1−α / 2 )
n
n
(2.3)
11.07
11.07
≤ µ ≤ 840.1 + 1.96
50
50
837.03 ≤ µ ≤ 843.17
El intervalo de confianza al nivel del 95% para la media de
82
los salarios de todos los docentes de esa universidad, es (837.03soles, 843.17 soles).
Ejemplo 2.4
Se diseñó un estudio de muestreo para estimar la deuda de tarjetas de crédito anual de los docentes universitarios peruanos. Una
muestra de 85 clientes docentes universitarios proporcionó los
balances de tarjetas de crédito que aparecen en la tabla siguiente.
Se va a construir un intervalo de confianza de 95% para la media
Tabla Nº 2.3. Balances de tarjeta de crédito en dólares anuales
para una muestra de 85 clientes docentes universitarios
9619
5994
3344
7888
7581
9980
5364
4652
13627
3091
12545
8718
8348
5376
968
943
7959
8452
7348
5998
4714
8762
2563
4935
381
7530
4334
1407
6787
5938
2998
3678
4911
6644
5071
5266
1686
3581
1920
7644
9536
10658
1962
5625
3780
11169
4459
3910
4920
5619
3478
7979
8047
7503
5047
9032
6185
3258
8083
1582
6921
13236
1141
8660
2153
5759
4447
7577
7511
8003
8047
609
4667
14442
6795
3924
414
5219
4447
5915
3470
7636
6416
6550
7164
poblacional del balance promedio poblacional de tarjetas de crédito por docente universitario.
Los cálculos para obtener la media y desviación estándar son
muy tediosos, por lo que nos auxiliaremos en el Software SPSS.
Los interesados en mayores detalles pueden remitirse a la biblio83
grafía: Estadística Descriptiva con soporte en SPSS y MATLAB
(Gómez et al., 2005).
Solución
a)
b)
Iniciar la sesión y activar SPSS.
Crear el archivo de datos con la variable balance, guardar y
ejecutar los siguientes comandos:
ANALIZE / DESCRIPTIVE STATISTICS / DESCRIPTIVES
/ Seleccionar la variable BALANCE / OPTIONS / activar
MEAN Y STD DEVIATION / CONTINUE / Y OK para ejecutar.
El output del SPSS es:
Mean
Std.
Deviation
5900
3058
donde la media y la desviación estándar en la muestra son:
x = 5900 y s = 3058 dólares.
El valor del cuantil z(1−α 2 ) de la distribución normal
z α = z0,975 = zteórico = 1.96 .
(1− )
2
Un intervalo para µ al nivel de confianza del 95% es:
x − z1−(α / 2 )
s
s
≤ µ ≤ x + z(1−α / 2 )
n
n
5900 − 1.96
3058
3058
≤ µ ≤ 5900 + 1.96
85
85
5900 − 650.78 ≤ µ ≤ 5900 + 650.78
5249.22 ≤ µ ≤ 6550.78
La media poblacional del valor de las tarjetas de crédito para
84
los docentes universitarios peruanos está entre 5249.22 y 6550.78
dólares anuales, con un nivel de confianza del 95%.
Intervalo de confianza para la proporción poblacional
Para estimar la proporción poblacional π, se usa el siguiente reπ −P
sultado: Por el capítulo 1 tenemos que P (1 − P ) ~ N (0,1) , a parn
tir del cual se construye el siguiente intervalo de confianza al nivel (1 − α ) , para la proporción poblacional π:
P − z(1−α / 2 )
P (1 − P )
P (1 − P )
≤ π ≤ P + z(1−α / 2 )
n
n
donde:
P es el estimador del parámetro proporción en la población, π;
z(1−α / 2 ) es el percentil de la distribución normal.
Ejemplo 2.5
En una encuesta de opinión, 320 estudiantes entrevistados de la
Facultad de Educación declararon estar a favor del candidato del
partido político de gobierno a la Presidencia de la República.
a. Hallar un intervalo de confianza, al nivel del 95% para estimar la proporción a favor.
b. Hallar un intervalo de confianza, al nivel del 99% para estimar la proporción a favor.
La muestra total fue de 400 estudiantes.
Solución
A un nivel de confianza del 95%, z(1−α / 2 ) = 1.96 .
La proporción de estudiantes que votan por el partido políti-
85
co en la muestra es p =
a 320
=
= 0.80 .
n 400
Un intervalo de confianza al nivel del 95%, para la proporción poblacional π es:
p − Z (1−α / 2 )
p (1 − p )
p (1 − p )
≤ π ≤ p + Z (1−α / 2 )
n
n
(2.4)
0.80(0.20 )
0.80(0.20 )
≤ π ≤ 0.80 + 1.96
400
400
0.80 − 1.96
0.7608 ≤ π ≤ 0.8392
El intervalo al nivel del 95% de confianza para la proporción
de estudiantes en la población que votan por el partido político es
( 76.08%, 83.92%).
Intervalo de confianza para la diferencia de medias de dos poblaciones
con varianzas conocidas
Si X 1 y X 2 son variables aleatorias independientes con distribu-
(
(
)
)
2
2
ciones N µ1 , σ 1 y N µ2 , σ 2 respectivamente; entonces, las me-
dias muestrales X 1 y X 2 , correspondientes a muestras aleatorias
 σ2 
de tamaño n1 y n2 , tienen las siguientes distribuciones N  µ1 , 1 
n1 

 σ2 
y N  µ2 , 2  . Luego, la variable aleatoria X 1 − X 2 es-tandarizan2 

da, Z =
(X
σ X 1− X 2 =
86
1
)
− X 2 − (µ1 − µ2 )
σ
σ2
+ 2
n1 n2
2
1
σ 12 σ 22
.
+
n1 n2
, tiene distribución N (0,1) , donde
Cabe señalar que si los tamaños de muestra son grandes, a
pesar de que las variables X 1 y X 2 no tienen distribución normal, la variable estandarizada, Z =
(X
1
)
− X 2 − (µ1 − µ2 )
tribución aproximadamente normal.
σ
σ2
+ 2
n1 n2
2
1
, tiene dis-
A partir de una muestra aleatoria de tamaño n1 para la variable X 1 y de una muestra de tamaño n2 para la variable X 2 , variables independientes, un intervalo para estimar la diferencia de
medias µ1 - µ2, al nivel de confianza del (1 − α )100% es:
x1 − x 2 − z(1−α / 2 )σ X 1 − X 2 ≤ µ1 − µ2 ≤ x1 − x 2 + z(1−α / 2 )σ X 1 − X 2 (2.5)
Ejemplo 2.6
En un sistema educativo se aplicaron dos métodos A y B para enseñar el curso de física. En un grupo de 80 estudiantes se aplicó el
método A y en el otro de 120 se aplicó el método B. Las medias de
las calificaciones obtenidas fueron 12.2 y 10.5 respectivamente.
¿Podemos admitir que los métodos de enseñanza no son diferentes y que las diferencias encontradas en las muestras se debe al
azar?. Experiencias anteriores dicen que las variables X 1 y X 2
que representan los rendimientos con los métodos A y B respectivamente, tienen distribución aproximadamente normal con desviaciones estándar σ 1 = 1.5 puntos y σ 2 = 0.5 puntos. α = 0.05 .
Construiremos un intervalo de confianza al 95% para la diferencia de los rendimientos promedio en la población.
Solución
Grupo 1
Grupo 2
n1 = 25
n2 = 20
x1 = 12.2 puntos
x 2 = 10.5 puntos
87
σ X 1− X 2
σ 12 σ 22
=
+
=
n1 n2
(15)2 + (0.5)2
25
20
= 0.09 + 0.0125 = 0.32
Basados en el teorema del límite central, el intervalo de confianza del 95% es:
x1 − x 2 − z(1−α / 2 )σ X 1 − X 2 ≤ µ1 − µ2 ≤ x1 − x 2 + z(1−α / 2 )σ X 1 − X 2 (2.6)
(12.2 − 10.5) + 1.96(0.32 ) ≤ µ1 − µ2 ≤ (12.2 − 10.5) + 1.96(0.32 )
1.7 − 0.6272 ≤ µ1 − µ2 ≤ 1.7 + 0.6272
1.0728 ≤ µ1 − µ2 ≤ 2.3272
Con una confianza del 95% la diferencia en los rendimientos
promedio de todos los estudiantes del curso de física está entre
1.07 puntos y 2.33 puntos.
Intervalo de confianza para la diferencia de medias de dos poblaciones
con varianzas desconocidas, muestras grandes (cualquier distribución)
Cuando se trata de muestras grandes con varianzas desconocidas, el intervalo de confianza al nivel (1 − α ) para la diferencia de
medias µ1 − µ2 es:
X 1 − X 2 − z(1−α / 2 ) S X 1 − X 2 ≤ µ1 − µ2 ≤ X 1 − X 2 + z(1−α / 2 ) S X 1 − X 2
donde:
S X 1− X 2 =
Ejemplo 2.7
88
S12 S22
+
.
n1 n2
En una muestra aleatoria de 36 alumnos de la maestría de
2
educación, la media de edades es x1 = 40 años y s1 = 9 años y
en otra muestra aleatoria de 49 alumnos en la maestría de ciencias
sociales, la media de edades de los alumnos es x1 = 35 años y des2
viación estándar s2 = 10 de años. Vamos a obtener el intervalo de confianza del 95% para la diferencia de medias en la población.
Solución
sX 1− X 2 =
s12 s22
9 10
+
=
+
= 0.6739
n1 n2
36 49
En muestras grandes, con el valor de y con los valores obtenidos
en la muestra se tiene:
( x1 − x2 ) − z(1−α / 2 ) s X 1 − X 2 < µ1 − µ2 < ( x1 − x 2 ) + z(1−α / 2 ) s X 1 − X 2 (2.7)
(40 − 35) − 1.96(0.6739 ) ≤ µ1 − µ2 ≤ ( 40 − 35) + 1.96(0.6739 )
3.679 ≤ µ1 − µ2 ≤ 6.321
Entonces, con un nivel de confianza del 95%, el intervalo para
la diferencia entre las medias de las edades de las dos poblaciones
de alumnos está entre 3.68 y 6.3 años.
Intervalo de confianza para la diferencia de medias de dos poblaciones
con varianzas desconocidas e iguales
(muestras pequeñas)
Como la varianza poblacional es desconocida, tiene que ser estimada y en lugar de la variable estandarizada Z, se tiene la variable aleatoria:
t=
( X 1 − X 2 ) − (µ1 − µ2 ) , cuya distribución es t-Student con
 1
1 
S p2  +


 n1 n2 
89
t
(n1 + n2 − 2 ) grados de libertad y se denota con ( n1+n2−2 ) . Como
hay n1 − 1 grados de libertad asociados con la muestra aleatoria
de la población 1, y n2 − 2 grados de libertad para la población 2,
la distribución t tendrá (n1 + n2 − 2) grados de libertad.
El estimador de la varianza poblacional es
S p2 =
(n − 1)S + (n − 1)S
n +n −2
2
1
1
1
1
2
2
.
2
2
Si S p es el estimador de σ 2 , entonces el estimador puntual
de σ X 1 − X 2 cuando σ 12 = σ 22 = σ 2 es S X X =
1− 2
1 1
S p2  +  .
 n1 n2 
Ahora se puede emplear la distribución t-Student para encontrar un intervalo de confianza para la diferencia entre las medias de las poblaciones.
Si se observa una muestra aleatoria de tamaño n1 para la variable X 1 y una muestra de tamaño n2 para la variable X 2 , donde
X 1 y X 2 son variables independientes con varianzas desconocidas, el intervalo para estimar la diferencia de medias µ1 − µ 2 , al
nivel de confianza (1 − α )100% es:
( x1 − x 2 ) − t(1−α / 2 ) s X 1 − X 2 ≤ µ1 − µ2 ≤ ( x1 − x 2 ) + t(1−α / 2 ) s X 1 − X 2 (2.8)
donde:
1 1
s X 1 − X 2 = s 2p  +  y para α > 0 , P (t( n1 +n2 −2 < tteórico ) = 1-α,
 n1 n2 
entonces en la tabla t-Student se encuentra el valor de t(1−α / 2 ) =
t(teórico) , la abscisa de la distribución t-Student con n1 + n2 − 2 grados de libertad.
Ejemplo 2.8
Con el fin de comparar los promedios de tiempo, en que los traba-
90
jadores de una determinada universidad de dos turnos diferentes
A y B, realizan una tarea, se registraron los tiempos correspondientes a 9 trabajadores de cada uno de los turnos. Para el turno A
se obtuvo:
32 min, 37min, 35min, 28min, 41min, 44min, 35min, 31min, 34min
y para el turno B: 35min, 31min, 29min, 25min, 34min, 40min,
27min, 32min, 31min.
Encontraremos un intervalo de confianza del 95% para la diferencia entre las medias de los tiempos de las tareas realizadas
por los trabajadores de los turnos A y B.
Solución
Supongamos que esos tiempos se distribuyen normalmente y que
las varianzas de los mismos son iguales. Utilizaremos el SPSS para
resolver encontrar las medias y varianzas de las muestras.
a) Iniciar la sesión y activarStatistics
SPSS.
Tiempo A
N
Mean
Std. Deviation
b)
Tiempo B
9
35.22
4.94
9
31.56
4.48
Crear el archivo de datos con las variables tiempoA y tiempoB. Después de crear la base de datos ejecutar los siguientes
comandos:
ANALIZE / DESCRIPTIVE STATISTICS / DESCRIPTIVES
/ Seleccionar las variables TIEMPOA y TIEMPOB/ OPTIONS / activar MEAN Y STD DEVIATION / CONTINUE / OK.
El output del SPSS nos muestra:
Se obtiene el valor de la varianza combinada:
s 2p =
(n1 − 1)s12 + (n2 − 1)s22
n1 + n2 − 2
=
8(4,94 ) + 8(4,48)
16
2
2
91
=
195.20 + 160.56 355.76
=
= 22.24 ,
16
16
y la estimación de la desviación estándar para la diferencia
de medias es:
1 1
1 1
s X 1 − X 2 = s 2p  +  = 22.24 +  = 4.89 = 2.21.
9 9
 n1 n2 
Con n1 + n2 − 2 = 9 + 9 − 2 = 16 grados de libertad, α = 0.05 ,
se cumple P t(16 ) < tteórico = 0.975, entonces en la tabla t-Student
(
)
se encuentra el valor de t(1−α / 2 ) = tteórico = 2.12 .
El intervalo de 95% de confianza para la diferencia de medias
poblacionales es:
( x1 − x 2 ) − t(1−α / 2 ) s X 1 − X 2 ≤ µ1 − µ2 ≤ ( x1 − x 2 ) + t(1−α / 2 ) s X 1 − X 2
(35.22 − 31.56) − (2.12)(2.21) ≤ µ1 − µ2 ≤ (35.22 − 31.56) + (2.12)(2.21)
− 1.03 ≤ µ1 − µ2 ≤ 8.35
Así, con un nivel de confianza del 95%, la diferencia de los
tiempos medios de las tareas realizadas para todos los trabajadores de los turnos A y B se encuentra entre -1.03 minutos y 8.3 minutos.
Intervalo de confianza para la diferencia entre las proporciones de dos
poblaciones
En las poblaciones 1 y 2, con respectivas proporciones poblacionales π 1 y π 2 (de estudiantes, profesores, etc., para ser más genéricos, de "unidades"), con determinados atributos; se desea encontrar un intervalo de confianza para la diferencia de proporciones
π1 − π 2 .
Los parámetros que son las proporciones poblacionales tienen como estimadores en cada una de las muestras: P1 =
92
A
y
n1
P2 =
B
, donde A es el número de elementos con el atributo de
n1
interés en la primera muestra y B es el número de elementos con
el mismo atributo en la segunda muestra. Cuando las muestras son
( P1 − P2 ) − (π 1 − π 2 )
tiene dis1 1
P (1 − P ) + 
nn1 P n+2 n P
tribución aproximadamente normal, donde P = 1 1  2 2 . Una
suficientemente grandes, la estadística
n1 + n2
n1 p1 + n2 p2
estimación común de π 1 = π 2 = π , es p =
.
n1 + n2
El intervalo de confianza (1 − α ) % para la diferencia de proporciones es:
( P1 − P2 ) − z(1−α / 2 ) S p ≤ π 1 − π 2 ≤ ( P1 − P2 ) + z(1−α / 2 ) S p ,
donde
1 1
S p = P(1 − P )  +  .
 n1 n2 
Ejemplo 2.9
Al Ministerio de Educación le interesa comparar la calidad del
trabajo que se realiza en las oficinas regionales rurales del norte y
del sur. Se seleccionan muestras aleatorias de expedientes de do-
Expedientes
Número expedientes analizados
Número de expedientes con errores
Oficina
regional norte
Oficina
regional sur
250
300
35
27
centes que trabajan en las áreas rurales norte y sur, que solicitan
traslado a áreas metropolitanas, para obtener un intervalo de confianza para la diferencia entre las proporciones de expedientes con
errores en las dos zonas rurales. A continuación se tiene el núme-
93
ro total de expedientes y el número de expedientes con errores en
cada una de las oficinas regionales.
Solución
π1: Proporción de expedientes con error en la oficina regional norte, en la población.
π2: Proporción de expedientes con error en la oficina regional sur,
en la población.
p1: Proporción de expedientes con error en la oficina regional norte, en la muestra.
p2: Proporción de expedientes con error en la oficina regional sur,
en la muestra.
p1 =
35
= 0.14
250
p2 =
27
= 0.09
300
p1 − p2 = 0.05
p=
sp =
n1 p1 + n2 p2
n1 + n2
p=
250(0.14) + 300(0.09)
= 0.1127
550
1 1
1
1 
p (1 − p )  +  = 0.1127 (0.8873) 
+
= 0.027

 250 300 
 n1 n2 
Para un nivel de confianza del 90%, en la tabla normal se
encuentra z(1−α / 2 ) = z0, 95 = 1.645 . Luego:
( p1 − p2 ) − z(1−α / 2 ) s p ≤ π 1 − π 2 ≤ ( p1 − p2 ) + z(1−α / 2 ) s p
(2.9)
( 0.14 − 0.09) − 1.645(0.0275) ≤ π 1 − π 2 ≤ ( 0.14 − 0.09) + 1.645(0.0275)
0.05 − 0.045 ≤ π 1 − π 2 ≤ 0.05 + 0.045
0.005 ≤ π 1 − π 2 ≤ 0.095
Con un nivel de confianza del 90%, la diferencia entre las tasas de errores de todos los trabajadores de las dos oficinas, se encuentra entre 0.5% y 9.5%.
Intervalo de confianza para la varianza de una población
94
En secciones anteriores describimos métodos de inferencia estadística, donde intervenían medias y proporciones poblacionales.
En esta sección ampliaremos el campo a casos donde intervienen
inferencias acerca de varianzas de la población.
En el capítulo anterior utilizamos la varianza muestral
S2 =
∑ (X
−X
n −1
i
) , como estimador puntual de la varianza pobla2
cional σ .
2
Figura Nº 3.1: Ejemplos de la Distribución Muestral de (n − 1)S 2 / σ 2
(Distribución Ji Cuadrado)
Con 2 grados de libertad
Con 5 grados de libertad
Con 10 grados de libertad
(n − 1)S 2
0
σ2
Siempre que se selecciona una muestra aleatoria simple del
tamaño n de una población normal, la expresión: (n − 1)
S2
, tiene
σ2
una distribución ji-cuadrado con n − 1 grados de libertad.
Usaremos el símbolo χα para representar el valor de la distribución Ji-cuadrado que da como resultado un área, o probabili2
Figura Nº 3.2: Distribución Ji cuadrado con
n − 1 grados de libertad
α /2
α /2
1−α
0
χα2 / 2
χ12−α / 2
95
dad, de α a la derecha del valor establecido.
2
Usando esta distribución se obtiene los percentiles χ (α / 2 ) y
χ (21−α / 2 ) de tal manera que cada una de las áreas que se indican en
la siguiente figura sean iguales a α / 2 .
Así que,

(n − 1)S 2 ≤ χ  = 1 − α
P  χα / 2 ≤
1−α / 2 
σ2


Luego, el intervalo para σ 2 , al nivel de confianza 1 − α , es:
(n − 1)S 2
≤σ
χ12−α / 2
2
(
n − 1)S 2
≤
χα2 / 2
,
donde los valores de χ son los percentiles de la distribución
chi-cuadrado con n − 1 grados de libertad, y 1 − α es el coeficiente
de confianza.
2
Ejemplo 2.10
Una muestra aleatoria de 20 estudiantes de la especialidad de biología ha rendido el examen de matemáticas, en el que ha obtenido
una media de x = 72 puntos con varianza s 2 = 16 puntos. Supondremos que las calificaciones se distribuyen normalmente y construiremos un intervalo de confianza para la varianza poblacional
de puntajes, σ 2 , con un nivel de confianza del 90%.
Solución
n = 20 ,
s 2 = 16 puntos2,
x = 72 puntos.
Para el nivel de confianza 1 − α = 0.95 , los valores de los per-
centiles de la distribución ji-cuadrado con n − 1 = 19 grados de libertad son χ 02.05 = 10.12 y χ 02.95 = 30.14 . Así:
(20 − 1)s 2
χ12−α / 2
96
≤σ2 ≤
(20 − 1)s 2
χα2 / 2
(2.10)
(20 − 1)16 ≤ σ 2 ≤ (20 − 1)16
30.14
10.12
10.09 ≤ ó 2 ≤ 30.04
Luego, con el nivel de confianza del 90%, la varianza poblacional de puntajes se encuentra entre 10.09 puntos2 y 30.04 puntos2.
Ejercicios
Para una muestra aleatoria de 6 estudiantes matriculados en el
curso de estadística se tiene los tiempos en horas semanales que
dedican a estudiar: 5 8 10 7 10 14
a. Defina la variable de interés.
b. Caracterice la media poblacional y la varianza poblacional.
c. ¿Cuál es el valor de la estimación puntual de la media de la
población? Interprete.
d. ¿Cuál es el valor de la estimación puntual de la desviación
estándar de la población?.
A una muestra aleatoria de 150 alumnos de la universidad,
se le preguntó si había estudiado el idioma inglés. 75 respondieron Sí, 55 respondieron No y 20 no opinaron.
a. ¿Cuál es el valor de la estimación puntual de la proporción
de la población que responde Sí?.
b. ¿Cuál es el valor de la estimación puntual de la proporción
de la población que respondió No?.
c. Encuentre el intervalo de confianza del 90% para la proporción poblacional que respondieron Sí.
Fuente de ingresos
Frecuencia
Propina sólo domingos
Quehaceres, dádivas y domingos
Quehaceres y dádivas, no domingos
Nada
149
219
251
165
Total
784
97
A una muestra aleatoria de 784 niños, cuyas edades fluctuaban de 9 a 14 años, se les preguntó en qué forma conseguían dinero de sus padres (Consumer Reports, enero de 1997). las respuestas fueron las siguientes:
a.
b.
c.
¿Qué proporción de niños recibe propina sólo los domingos?.
¿Qué proporción de niños recibe dinero por quehaceres y dádivas, pero no recibe los domingo?
¿Qué proporción de niños recibe dinero por quehaceres, dádivas y también domingos?
El departamento de transporte en Estados Unidos, publica
estadísticas de llegadas, antes o después del horario programado,
de los principales vuelos ( Associated Press, 8 de septiembre de
2000). Suponga que la proporción estimada de vuelos que llegan
a tiempo, para todas las aerolíneas, se basa en una muestra aleatoria de 1400 vuelos. Si 1117 llegan a tiempo, ¿cuál es la estimación
puntual de la proporción de vuelos que llegan a tiempo?.
Encuentre el intervalo de confianza del 90% para la proporción poblacional de vuelos que llegan a tiempo.
Louis Harris encuestó a una muestra aleatoria de 108 adultos
para conocer su opinión acerca de la educación (Education Week,
7 de agosto de 2000). Las respuestas fueron las siguientes:
595 adultos: la está mejorando
332 adultos: la educación permanece igual.
81 adultos: la educación está empeorando.
Encuentre la estimación puntual de los siguientes parámetros
de la población:
a. La proporción de adultos que opinan que la educación está
mejorando.
b. La proporción de adultos que piensan que la educación permanece igual.
c.
La proporción de adultos que piensan que la educación está
98
empeorando.
Para estimar la media del consumo (dólares) en el restaurante
de una gran universidad, se tomó una muestra de 49 profesores.
Suponga una desviación estándar poblacional de 5 dólares.
Si la media en la muestra fue 24.80 dólares mensuales. ¿Cuál
fue el intervalo de confianza del 95% para el consumo medio poblacional?.
En una muestra aleatoria de 20 alumnos en el curso de estadística aplicada a la educación, se encontró una media de 70 puntos y una desviación típica de 9 puntos en las calificaciones finales. Encuentre el intervalo de confianza del 90% para la media de
todas las calificaciones, suponiendo que se distribuyen normalmente.
Quince alumnos de un colegio fueron pesados, obteniéndose:
42.70 kg. 43.48 kg 49.68 kg. 42.78 kg. 43.18 kg. 42.56 kg. 42.76 kg.
42.87 kg. 42.95 kg. 43.39 kg. 42.01 kg. 43.06 kg. 41.60 kg. 43.20 kg.
43.10 kg. Suponiendo que los pesos se distribuyen normalmente,
obtenga el intervalo de confianza del 99% para la media de los
pesos de todos los estudiantes del colegio.
Los estudiantes de la Facultad de Educación de una universidad de prestigio pudieron elegir entre un curso de estadística sin laboratorio de tres horas semanales y otro curso de
estadística con laboratorio de cuatro horas semanales. El examen escrito final fue el mismo para las dos secciones. Si 12 estudiantes de la sección con laboratorio tuvieron una calificación promedio de 84 con una desviación estándar de 4, y 18 estudiantes de
la sección sin laboratorio alcanzaron una calificación promedio de
77 con una desviación estándar de 6, encuentre un intervalo de
confianza del 99% para la diferencia entre las calificaciones promedio de los dos cursos. Suponga que las poblaciones se distribuyen de manera aproximadamente normal con varianzas iguales.
En un estudio que realizó la universidad de Cornell acerca de
las diferencias salariales entre hombres y mujeres se dio a conocer
que una de las razones por las que los salarios de los hombres
sean mayores que los salarios de las mujeres es que, los hombres
99
Hombres
Mujeres
x1 = 14.9 años de trabajo
x 2 = 10.3 años de trabajo
s1 = 5.2
s2 = 3.8 años
n1 = 100
n2 = 85
tienden a acumular más años de experiencia que las mujeres (Business Wek, 28 de agosto de 2000). Se tomaron dos muestras aleatorias independientes y se encontró:
a.
b.
¿Cuál es la estimación puntual de la diferencia de medias
poblacionales de los salarios de hombres y mujeres?.
Encuentre el intervalo de confianza del 95% para la diferencia entre las dos medias poblacionales.
Un grupo de investigadores desea estimar la diferencia entre
las medias de los ingresos anuales de familias en dos zonas de
Zona 1
x1 = 15 700
s1 = 700
n1 = 8
soles
soles
Zona 2
x 2 = 14 500
soles
s2 = 14 500
soles
n2 = 12
Lima Metropolitana. En muestras aleatorias independientes de
familias residentes en las dos zonas se encontró los siguientes resultados:
a.
b.
c.
100
Encontrar la estimación puntual para la diferencia entre las
medias de los ingresos de las dos zonas
Determine un intervalo de confianza del 95% para esa diferencia?.
¿Qué suposiciones hizo para encontrar el intervalo en el
inciso b?.
Una encuesta de Gallup, en 1994, determinó que el 16% de
505 varones y 25% de 496 mujeres encuestados en una universidad, estuvieron a favor de prohibir la venta libre de cerveza, vinos y licores en el país. Encuentre un intervalo de confianza de
95% para la diferencia entre las proporciones de mujeres y varones de esa universidad que estuvieron a favor de la prohibición.
Usted es un inspector de escuelas públicas y realiza un experimento para investigar si la habilidad en lectura de los estudiantes
de primer año de secundaria ha mejorado o no. Si en una muestra
aleatoria de 185 estudiantes de esta población encuentra una habilidad media de lectura igual a 75 palabras por minuto, encuentre el
intervalo de confianza del 90% para la habilidad media en lectura
de todos los estudiantes de primer año de secundaria.
El Director Académico del centro pre universitario de la UFV
tiene la percepción que el rendimiento académico durante el primer año de estudios en la universidad, de los alumnos ingresantes a través de la institución que dirige, ha sufrido cambios en los
últimos años. Para confirmar su percepción llevó a cabo un estudio, para el que escogió una muestra aleatoria de 150 alumnos
que ingresaron el año 2004 a través del centro pre universitario y
pidió al sistema de matrícula el rendimiento de cada uno de estos
alumnos durante el año académico 2004. Para dicha muestra obtuvo de rendimiento promedio 14.5 puntos con desviación estándar 0.5 puntos. Suponga normalidad y encuentre el intervalo de
confianza del 90% para la media poblacional del rendimiento.
Caracterice con precisión los parámetros poblacionales.
Para determinar el efecto sobre el desarrollo psicológico de
los escolares que tienen que viajar a la escuela en ómnibus de servicio público, se tomó una prueba de ansiedad a un grupo de 40
escolares que usan este sistema de transporte y a 30 escolares que
en ómnibus
x1 = 145
caminando
x2 = 135
101
van caminando al colegio. Se sabe que las desviaciones estándar
en ambas poblaciones son 9 y 12 respectivamente.
Los resultados de la prueba de ansiedad son los siguientes:
Suponiendo normalidad, encuentre un intervalo de confianza del 90% para la diferencia entre las ansiedades medias. Use.
Antes de aplicar el Plan Huascarán en el distrito de Cajatambo, el rendimiento promedio de los estudiantes de primer año de
primaria era de 12 puntos. Para determinar si el Plan ha sido efectivo en el incremento del rendimiento de los estudiantes, se observaron al azar a 150 estudiantes después de aplicar el plan durante
un año académico, obteniéndose de rendimiento promedio 13.5
puntos con desviación estándar 2.1 puntos. Encuentre el intervalo
de confianza para el rendimiento promedio. Use la metodología
correspondiente para dar respuesta a la pregunta planteada y de
ser necesario suponga normalidad.
Un investigador en el campo educativo sostuvo que el módulo didáctico empleado en la enseñanza de matemáticas es uno de
los factores que influye y determina en el proceso de enseñanza
aprendizaje y por lo tanto, el módulo adoptado incide en el rendimiento académico de los estudiantes. Para verificar su hipótesis
realizó el siguiente experimento: durante un semestre se llevó a
cabo el trabajo lectivo para dos grupos de estudiantes de la misMétodo A
12
13
12
10
10
13
13
11
14
Método B
16
17
117
14
15
17
16
16
15
ma carrera en la misma universidad, empleando dos módulos (A
y B) de características bien diferenciadas. Al final del curso aplicó
el mismo examen y obtuvo las siguientes notas.
Suponiendo que las muestras provienen de poblaciones normales con varianzas iguales, construya el intervalo de confianza
del 90% para la diferencia de medias poblacionales.
102
Un grupo de 350 estudiantes fueron divididos aleatoriamente en dos subgrupos de 100 y 150 estudiantes. Los de la muestra 1
aprendieron determinado material en el cual se enuncia verbalmente el concepto de transitivitas de "más alto que", a continuación de lo cual se dieron varios ejemplos de la situación; a los estudiantes del grupo 2 se les expuso ejemplos tras de lo cual se
enunció verbalmente el concepto. Son dos las poblaciones subyacentes a las muestras y que hubieran podido participar en el experimento. Al finalizar el experimento, 62 estudiantes de la muestra
1 y 70 estudiantes de la muestra 2 dominaban el concepto de transitividad. Encuentre un intervalo de confianza del 95% para la diferencia de proporciones poblacionales. Previamente caracterice
los parámetros poblacionales.
103