( y ( (a) Determine las ecuaciones del plano BDG y de la recta EC
Anuncio
FACULTAD DE ARQUITECTURA – UNIVERSIDAD DE LA REPÚBLICA Examen de Matemática – 16 XII 2009
EJERCICIO I
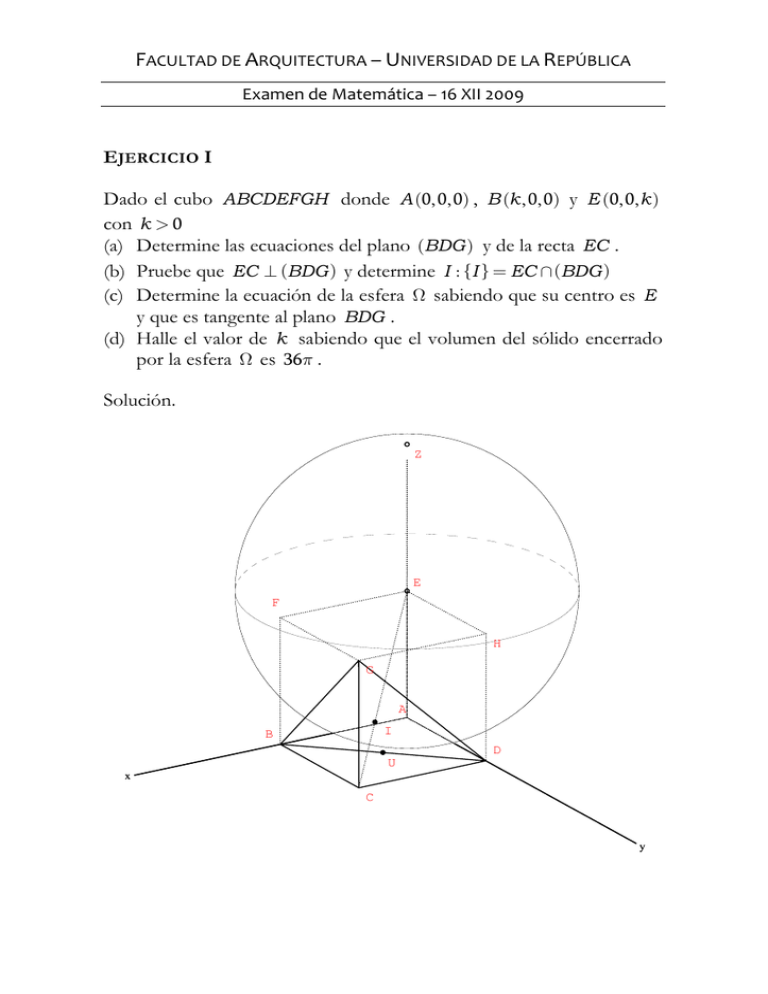
Dado el cubo ABCDEFGH donde A (0, 0, 0) , B (k , 0, 0) y E (0, 0, k )
con k > 0
(a) Determine las ecuaciones del plano (BDG ) y de la recta EC .
(b) Pruebe que EC ⊥ (BDG ) y determine I : {I } = EC ∩ (BDG )
(c) Determine la ecuación de la esfera Ω sabiendo que su centro es E
y que es tangente al plano BDG .
(d) Halle el valor de k sabiendo que el volumen del sólido encerrado
por la esfera Ω es 36π .
Solución.
Z
E
F
H
G
A
I
B
D
U
x
C
y
Solución Examen de Matemática – Diciembre 2009
Parte (a)
B (k , 0, 0) , D (0, k , 0) , G (k , k , k )
Plano (BDG ) : x + y − z = k
E (0, 0, k ) , C (k , k , 0)
Recta EC : x = λ , y = λ , z = k − λ , λ ∈ R
Parte (b)
G
G
n(BDG ) ⊥ (BDG ) , n(BDG ) = (1, 1, −1)⎪⎫⎪
G
G
⎬ ⇒ n(BDG ) = v EC ⇒ EC ⊥ (BDG )
G
G
⎪⎪⎭
v EC & EC , v EC = (1, 1, −1)
{I } = (BDG ) ∩ EC
⎧⎪x + y − z = k
⎪⎪
⎪⎪x = λ
2k
→ λ + λ − (k − λ) = k ⇒ 3λ = 2k ⇒ λ =
⎨
⎪⎪y = λ
3
⎪⎪
⎪⎩z = k − λ
⎛ 2k 2k k ⎞⎟
I = ⎜⎜ ,
,
⎝ 3 3 3 ⎠⎟⎟
Parte (c)
ρ : radio de Ω
ρ = dist (E , I )
⎛ 2k 2k k ⎞⎟ ⎛ −2k −2k 2k ⎞⎟
E − I = (0, 0, k ) − ⎜⎜ ,
, =⎜
,
, ⎟⎟
⎝ 3 3 3 ⎠⎟⎟ ⎝⎜ 3
3
3 ⎠
2k
⎛ 2k ⎞2
k > 0, ρ = 3 ⎜⎜ ⎟⎟⎟ = 3
⎝3⎠
3
⎛ 2k ⎞2
Ω : x 2 + y 2 + (z − k )2 = ⎜⎜ 3 ⎟⎟⎟
⎝
3 ⎠
Ω : x 2 + y 2 + (z − k )2 =
Parte (d)
VΩ =
4k 2
3
4 3
πρ
3
4 ⎛ 2k ⎞⎟3 4 ⎜⎛
8k 3 ⎞⎟ 32 3
3 3
⎟=
π ⎜⎜ 3 ⎟⎟ = π ⎜3 3
πk 3 = 36π ⇒ k =
3 ⎝
3⎠
3 ⎜⎝
27 ⎠⎟⎟
27
2
Facultad de Arquitectura – Universidad de la República
Página | 2
Solución Examen de Matemática – Diciembre 2009
EJERCICIO II
Sea R la región del plano XOY cuya área se expresa por
A (R ) =
Página | 3
(a)
(b)
(c)
(d)
∫
1
dx
0
∫
−2 x 2 + 4 x +2
1− 1−(x −1)2
dy +
∫
2
dx
1
∫
−3 x +7
1− 1−(x −1)2
dy
Represente la región R en un sistema de coordenadas cartesianas.
Plantee A (R ) invirtiendo el orden de integración.
Calcule A (R )
Realice un bosquejo del cuerpo cuyo piso es R y su techo está
dado por
z = 3 ∀y / y ≤ 1 ∧ z = 4 − y ∀ y / y > 1
(e) Plantee por integrales dobles el volumen de dicho cuerpo
(f) Calcule el volumen.
Solución
Parte (a)
y
x
Parte (b)
∫
1
0
dy
∫
1+ 1−(y −1)2
1− 1−(y −1)2
dx +
∫
1
2
dy
∫
7 −y
3
0
dx +
∫
4
2
dy
∫
7−y
3
1− 2−
y
2
dx
Facultad de Arquitectura – Universidad de la República
Solución Examen de Matemática – Diciembre 2009
Parte (c)
π 23
+
2
6
A (R ) =
Parte (d)
z
Página | 4
y
x
Parte (e)
V=
∫
2
dx
0
∫
1
1− 1−(x −1)2
3dy +
∫
1
0
dx
∫
−2 x 2 + 4 x +2
(4 − y )dy +
1
+
∫
1
2
dx
∫
−3 x +7
(4 − y )dy
1
Parte (f)
A=
3π 71
+
2 10
Facultad de Arquitectura – Universidad de la República
Solución Examen de Matemáttica – Diciembre 2009
EJER
RCICIO III
Se considera la rregión D de la figura
fi
adjunta.
Sus bordes estáán dados por las
l
siguientes
ecuaciones:
Página | 5
y = 4 − x 2 , y = 5 − 4 − x 2 , x = 2 , x = −2
(a) Plantee
P
por
in
ntegrales
dobless,
en
los
do
os
ordenes,
∫∫ f (x , y )dxdy .
D
(b) Determine,
D
justificcadamente, el valo
or de la integral doble
d
anterior
f (x , y ) = −x .
cuando
c
(c) Halle
H
el valor de
d la integral doble cuando f (x , y ) = y 2 . Se
recomienda
r
no callcular directamentee la integral.
∫∫ (2y − 5) dxddy < 4 ∫∫ y dxdyy
2
(d) Explique
E
por qué
sin calcular
2
D
D
las
l integrales.
Soluución
Partte (a)
∫∫
f (x , y )dydx =
∫∫
f (x , y )dxdy =
D
D
+
∫
∫
2
∫
2
−2
3
2
dx
dy
0
d
dy
∫
∫
∫
2
−2
5− 4−x 2
4 −x 2
− 4−y 2
−2
f (x , y )dy
f (x , y )dx +
f (x , y )dx +
∫
5
dy
3
+
∫
3
5
dy
∫
∫
∫
2
dy
0
∫
2
4−y 2
− 4−(y −5)2
−2
2
4−(y −5)2
f (x , y )dx +
f (x , y )dx +
f (x , y )dx
Facultad de Arrquitectura – Univversidad de la Repúública
Solución Examen de Matemática – Diciembre 2009
Parte (b)
∫∫ −xdxdy = −M
y
(D )
D
Como la región D es simétrica respecto al eje OY , M y (D ) = 0 ,
entonces
Página | 6
∫∫ −xdxdy = 0
D
Parte (c)
∫∫ y dxdy = I
2
x
(D )
D
Considerando D compuesta por figuras simples:
D1 rectángulo, D2 semicírculo de diámetro OX , D2 semicírculo de
diámetro incluido en la recta y = 5 , se obtiene
4 × 53
3
π × 24
I x (D2 ) =
= 2π
8
4 × 2 ⎞⎟2 ⎛ 4 × 2 ⎞⎟2 ⎤ ⎜⎛ π × 22 ⎞⎟
160
π × 24 ⎡⎛
⎟ = 52π −
I x (D3 ) =
+ ⎢⎜⎜5 −
⎟⎟ − ⎝⎜⎜
⎟⎟ ⎥⎥ ⎜⎜
⎟
⎢
⎟
⎝
⎠
⎠
8
3π
3π ⎦ ⎝ 2 ⎠
3
⎣
I x (D1 ) =
I x (D ) = I x (D1 ) − I x (D2 ) − I x (D3 )
I x (D ) = 220 − 54 π
Facultad de Arquitectura – Universidad de la República
Solución Examen de Matemática – Diciembre 2009
Parte (d)
Es conocido que
I xG (D ) < I x (D )
Planteando lo anterior utilizando la definición de momento de inercia
Página | 7
∫∫
D
5 ⎞2
⎛
⎜⎜y − ⎟⎟⎟ dxdy <
⎝
2⎠
∫∫ y dxdy
2
D
Desarrollando el integrando del primer miembro
∫∫
D
(2y − 5)2
dxdy <
4
∫∫ y dxdy
2
D
Por linealidad
1
4
∫∫ (2y − 5) dxdy < ∫∫ y dxdy
2
D
2
D
Multioplicando ambos miembros por 4
∫∫ (2y − 5) dxdy < 4 ∫∫ y dxdy
2
D
2
D
Facultad de Arquitectura – Universidad de la República