La parábola es el conjunto de puntos tales que la distancia de
Anuncio
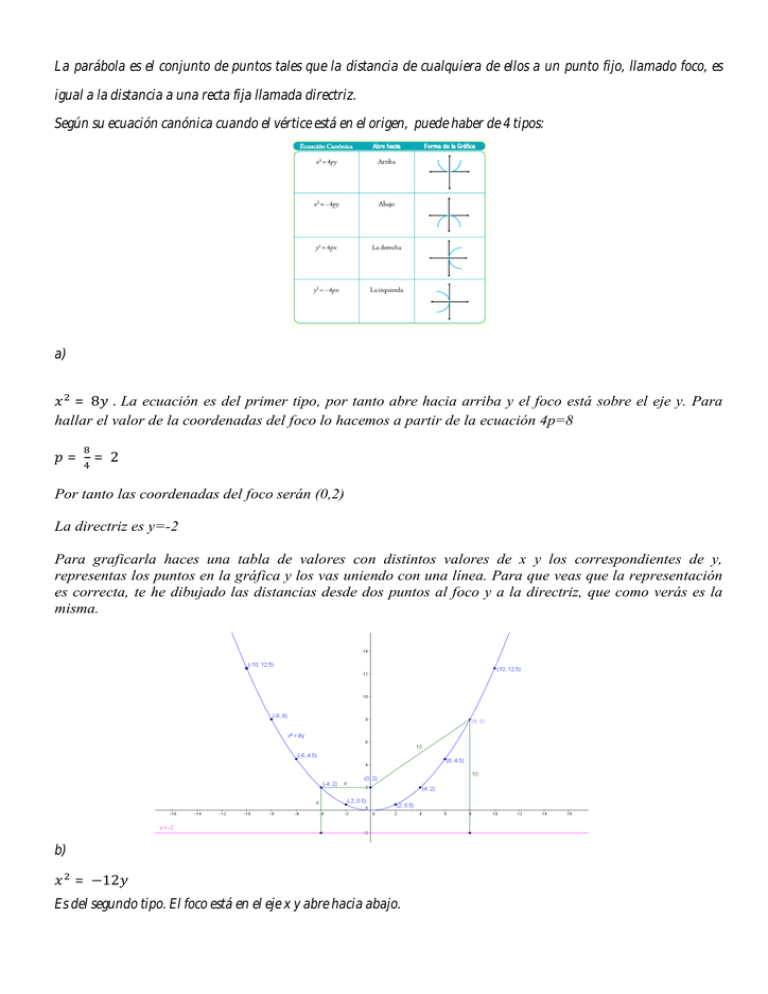
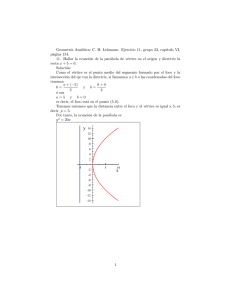
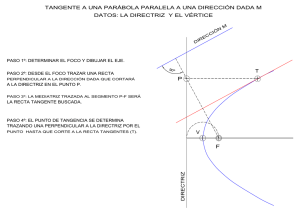
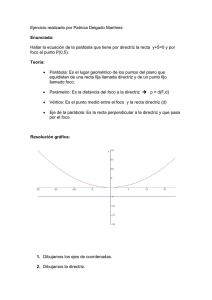
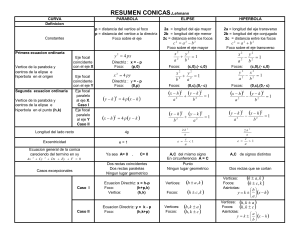
La parábola es el conjunto de puntos tales que la distancia de cualquiera de ellos a un punto fijo, llamado foco, es igual a la distancia a una recta fija llamada directriz. Según su ecuación canónica cuando el vértice está en el origen, puede haber de 4 tipos: a) = 8 . La ecuación es del primer tipo, por tanto abre hacia arriba y el foco está sobre el eje y. Para hallar el valor de la coordenadas del foco lo hacemos a partir de la ecuación 4p=8 = =2 Por tanto las coordenadas del foco serán (0,2) La directriz es y=-2 Para graficarla haces una tabla de valores con distintos valores de x y los correspondientes de y, representas los puntos en la gráfica y los vas uniendo con una línea. Para que veas que la representación es correcta, te he dibujado las distancias desde dos puntos al foco y a la directriz, que como verás es la misma. b) = −12 Es del segundo tipo. El foco está en el eje x y abre hacia abajo. 4 = −12 = = −3 Luego las coordenadas del foco son (0,-3) La recta directriz será y =3