resumen conicas

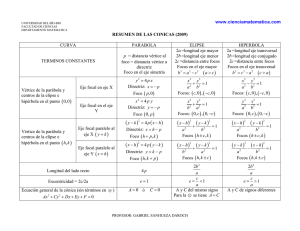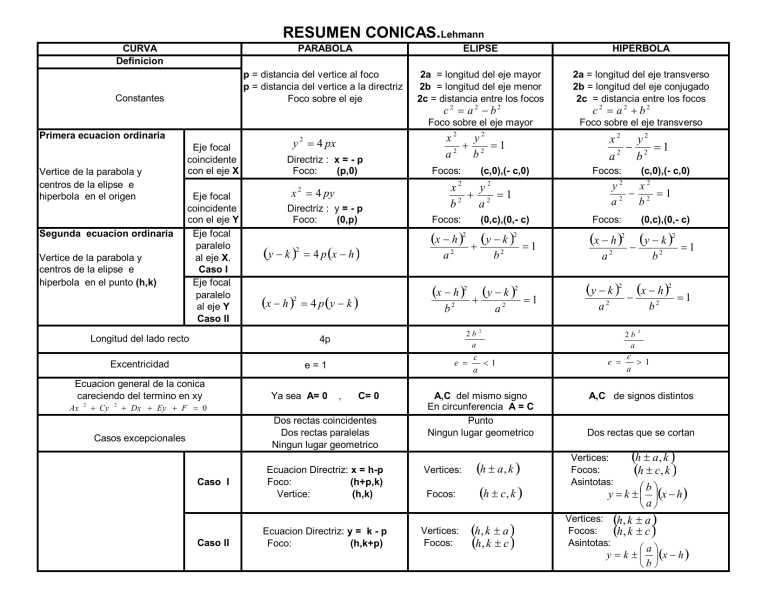
RESUMEN CONICAS.Lehmann
CURVA
Definicion
Constantes
PARABOLA
ELIPSE
HIPERBOLA
p = distancia del vertice al foco
p = distancia del vertice a la directriz
Foco sobre el eje
2a = longitud del eje mayor
2b = longitud del eje menor
2c = distancia entre los focos
2a = longitud del eje transverso
2b = longitud del eje conjugado
2c = distancia entre los focos
c2  a2  b2
c2  a2  b2
Foco sobre el eje mayor
Primera ecuacion ordinaria
Vertice de la parabola y
centros de la elipse e
hiperbola en el origen
Segunda ecuacion ordinaria
Vertice de la parabola y
centros de la elipse e
hiperbola en el punto (h,k)
Eje focal
coincidente
con el eje X
Eje focal
coincidente
con el eje Y
Eje focal
paralelo
al eje X.
Caso I
Eje focal
paralelo
al eje Y
Caso II
Longitud del lado recto
 Cy
2
Directriz : x = - p
Foco:
(p,0)
x 2  4 py
Directriz : y = - p
Foco:
(0,p)
y  k 2
2
x  h 
 4 p x  h 
 4 p y  k 
Ya sea A= 0
Focos:
,
C= 0
Dos rectas coincidentes
Dos rectas paralelas
Ningun lugar geometrico
Caso I
Caso II
Foco sobre el eje transverso
x2 y2

1
a2 b2
x
y
 2 1
2
a
b
(c,0),(- c,0)
Focos:
Focos:
y
x2

1
a2 b2
(0,c),(0,- c)
x  h 2  y  k 2
a2
b2
x  h 2
b2
1
2

y  k

a2
1
Focos:
c
1
a
A,C del mismo signo
En circunferencia A = C
Punto
Ningun lugar geometrico
Ecuacion Directriz: x = h-p
Foco:
(h+p,k)
Vertice:
(h,k)
Vertices:
h  a , k 
Focos:
h  c , k 
Ecuacion Directriz: y = k - p
Foco:
(h,k+p)
Vertices:
Focos:
(0,c),(0,- c)
x  h 2  y  k 2
a2
b2
y  k 2  x  h 2
a2
2
h, k  a 
h , k  c 
(c,0),(- c,0)
2
x2
y2

1
b2
a2
e 
 Dx  Ey  F  0
Casos excepcionales
2
2b
a
e=1
Ecuacion general de la conica
careciendo del termino en xy
2
y 2  4 px
4p
Excentricidad
Ax
2
b2
2b
a
e 
1
1
2
c
1
a
A,C de signos distintos
Dos rectas que se cortan
Vertices:
Focos:
Asintotas:
h  a , k 
h  c , k 
b
y  k   x  h 
a
Vertices: h , k  a 
Focos:
h , k  c 
Asintotas:
a
y  k    x  h 
b