Table of derivatives
Anuncio

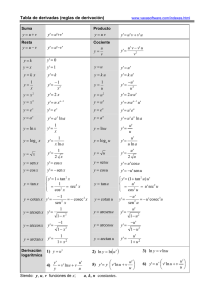
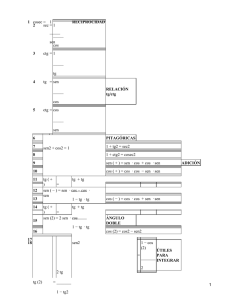
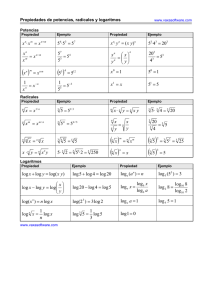
Table of derivatives www.vaxasoftware.com Addition y =u+v Multiplication y=uv y ' = u'+ v ' Subtraction y =u−v y ' = u ' v + v' u Division y ' = u'− v ' y= u v y' = u ' v − v' u v2 y=k y' = 0 y=x y' = 1 y=u y' = u' y=k x y' = k y=ku y' = k u' y = x2 −1 x2 y' = 2 x y = u2 − u' u2 y' = 2 u u' y = xn y ' = n x n −1 y = un y ' = n u n−1 u ' y = ex y' = e x y = eu y '= u ' eu y = ax y '= a x ln a y = au y '= u ' a u ln a y = ln x y' = 1 x y = ln u y' = y = log a x y' = 1 x ln a y = log a u y' = u' u ln a y= y '= y= u y '= u' 2 u y = sin u y ' = u ' cos u y = cos u y ' = −u ' sin u y= 1 x y= y' = x 1 y = sin x 2 x y ' = cos x y = cos x y ' = − sin x y = tan x ⎧ y ' = 1 + tan 2 x ⎪ 1 ⎨ 2 ⎪⎩ = cos 2 x = sec x y = cotan x y ' = y = arcsin x y ' = y = arccos x y' = y = arctan x y' = Generalized power rule −1 = − cosec2 x 2 sin x 1 1− x2 −1 1− x 2 1 1+ x2 1) y = u v 4) y' u' = v' ln u + v y u Where: y, u, v are functions of x; 1 u y' = u' u y = tan u ⎧ y ' = (1 + tan 2 u ) u ' ⎪ u' ⎨ 2 ⎪⎩ = cos 2 u = u ' sec u y = cotan u y' = y = arcsin u y' = y = arccos u y' = y = arctan u y' = − u' = − u ' cosec 2u 2 sin u u' 1 − u2 −u' 1 − u2 u' 1 + u2 2) ln y = ln( u v ) 3) ln y = v ln u u' ⎞ ⎛ 5) y ' = y ⎜ v' ln u + v ⎟ u ⎠ ⎝ u' ⎞ ⎛ 6) y ' = u v ⎜ v' ln u + v ⎟ u ⎠ ⎝ a, k, n are constants. www.vaxasoftware.com