Funciones hiperbólicas sinh x = cosh x = tanh x = y además cosech
Anuncio

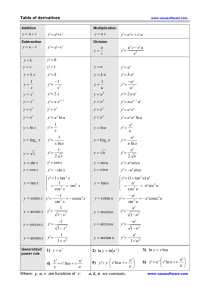
Funciones hiperbólicas
sinh x =
ex −e−x
2
cosh x =
ex +e−x
2
tanh x =
sinh x
cosh x
y además cosech x =
1
sinh x ,
sech x =
1
cosh x
y cotanh x =
1
tanh x .
Se tienen las siguientes igualdades:
cosh2 x − sinh2 x = 1, sech2 x + tanh2 x = 1 y cotanh2 x − cosech2 x = 1.
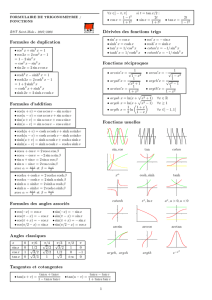
Primitivas
R
1. dx = x + C
R
n+1
2. xn dx = xn+1 + C si n ∈ R \ {−1}.
R
3. x1 dx = ln|x| + C.
R
n+1
4. tn dt = tn+1 + C si n ∈ R \ {−1}.
R
5. 1t dt = ln|t| + C.
R
6. et dt = et + C.
R
at
+ C.
7. at dt = lna
R
8. cost dt = sint + C.
R
9. sint dt = −costdt.
R
R
R
10. cos12 t dt = sec2 t dt = (1 + tan2 t) dt = tant + C.
R
R
11. sin12 t dt = cosec2 t dt = −cott + C.
R 1
12. √1−t
2 dt = arcsint + C.
R 1
13. 1+t2 dt = arctant + C.
R
14. cosht dt = sinht + C.
R
15. sinht dt = coshtdt.
R 1
16. cosh
2 t dt = tanht + C.
R 1
17. sinh2 t dt = cotht + C.
R 1
18. √1+t
dt = arcsinht + C.
2
R 1
19. √t2 −1 dt = arccosht + C.