AGRO 5005

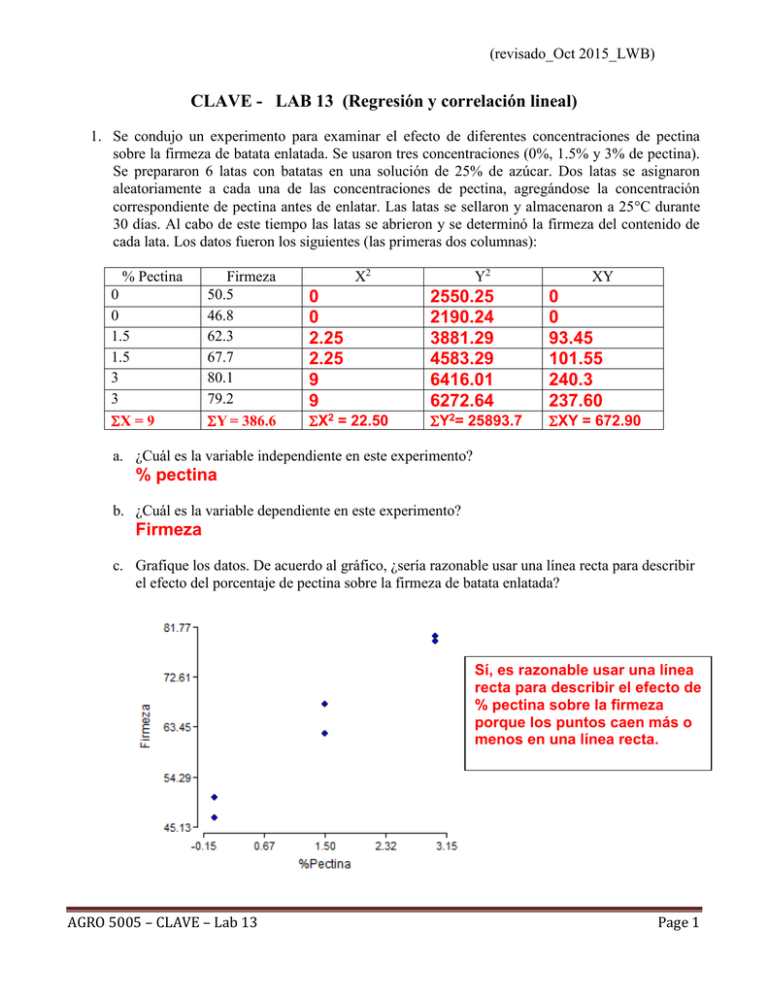
(revisado_Oct 2015_LWB)
CLAVE - LAB 13 (Regresión y correlación lineal)
1. Se condujo un experimento para examinar el efecto de diferentes concentraciones de pectina
sobre la firmeza de batata enlatada. Se usaron tres concentraciones (0%, 1.5% y 3% de pectina).
Se prepararon 6 latas con batatas en una solución de 25% de azúcar. Dos latas se asignaron
aleatoriamente a cada una de las concentraciones de pectina, agregándose la concentración
correspondiente de pectina antes de enlatar. Las latas se sellaron y almacenaron a 25C durante
30 días. Al cabo de este tiempo las latas se abrieron y se determinó la firmeza del contenido de
cada lata. Los datos fueron los siguientes (las primeras dos columnas):
% Pectina
0
0
1.5
1.5
3
3
X = 9
Firmeza
50.5
46.8
62.3
67.7
80.1
79.2
Y = 386.6
X2
Y2
XY
0
0
2.25
2.25
9
9
2550.25
2190.24
3881.29
4583.29
6416.01
6272.64
0
0
93.45
101.55
240.3
237.60
X2 = 22.50
Y2= 25893.7
XY = 672.90
a. ¿Cuál es la variable independiente en este experimento?
% pectina
b. ¿Cuál es la variable dependiente en este experimento?
Firmeza
c. Grafique los datos. De acuerdo al gráfico, ¿sería razonable usar una línea recta para describir
el efecto del porcentaje de pectina sobre la firmeza de batata enlatada?
Sí, es razonable usar una línea
recta para describir el efecto de
% pectina sobre la firmeza
porque los puntos caen más o
menos en una línea recta.
AGRO 5005 – CLAVE – Lab 13
Page 1
(revisado_Oct 2015_LWB)
d. Complete la tabla arriba con los valores indicados. Use estos valores para determinar las
siguientes cantidades:
i.
Sxx = la suma de cuadrados (“corregida”) de X = 9.00
ii.
Syy = la suma de cuadrados (“corregida”) de Y =983.79
iii.
Sxy = la suma de productos = XY – [(X)(Y)/n] =
672.90 –[(9)(386.6)/6] = 93
iv.
̅ = 1.5
𝑿
v.
̅ = 64.433
𝒀
vi.
̂ 1 = Sxy/ Sxx = 93/9.00 = 10.33 (pendiente o coeficiente de
𝜷
regresión)
vii.
̂0 = 𝒀
̂ 1𝑿
̅-𝜷
̅ = 64.433 – [10.33(1.5)] = 48.938 (intercepto)
𝜷
Para obtener los valores arriba, se puede hacer los cálculos a mano, o usar InfoStat para calcular
los valores de X2, Y2 y XY (usando la opción de “Formula”)
Luego, se puede determinar los valores de X, Y, X2, Y2, XY
Acuérdese que en InfoStat “Suma Cuad” refiere a la suma de los cuadrados (por ejemplo, X), mientras
que “SCC” (“suma de cuadrados corregidas” = S.C.) calcula los valores que normalmente llamamos
“suma de cuadrados” (la suma de cuadrados de desviaciones de la media)
AGRO 5005 – CLAVE – Lab 13
Page 2
(revisado_Oct 2015_LWB)
Variable
pectina
firmeza
pect_cuadrado
firm_cuadrado
pectxfirm
Suma
Suma Cuad.
SCC
9.00
22.50
9.00
386.60
25893.72
983.79
22.50
172.13
87.75
25893.72 127883082.50 16135626.59
672.90
133243.16
57777.42
e. ¿Cuál es la ecuación lineal estimada para estos datos?

 

Y  B0  B1 x , donde x=Pectina, Y =Firmeza
Yˆ  48.93  10.33x
f. Formule y pruebe las hipótesis de interés usando =.05.
Haciendo los cálculos a mano tenemos:
SCregresion
SCerror
SCtotal
̂ 1 Sxy = 10.33 * 93 = 960.69
=𝜷
= SCtotal - SCregresión = 983.79 – 960.69 = 23.1
= Syy = 983.79
CMregresión = SCregresión/GLregresión = 960.69/1 = 960.69
CMerror = SCerror/GLerror = 23.1/ 6-2 = 5.775
Fobservado = CMregresión/ CMerror = 960.69/5.775 = 166.353 (hay un poco de error de
redondeo)
Ftabular con 1gl y 4 gl = 7.71 (se rechaza la Ho – hay evidencia de una relación lineal)
En InfoStat:
AGRO 5005 – CLAVE – Lab 13
Page 3
(revisado_Oct 2015_LWB)
Análisis de regresión lineal
Variable
N
R² R² Aj ECMP AIC BIC
Firmeza
6
0.98 0.97 11.04 31.04 30.41
Coeficientes de regresión y estadísticos asociados
Coef
Est. E.E. LI(95%)
LS(95%)
T
p-valor
const
48.93 1.54
44.66
53.21
31.76 <0.0001
Pectina
10.33 0.80
8.12
12.54
12.99 0.0002
Cuadro de Análisis de la Varianza (SC tipo III)
F.V.
SC
gl
CM
F
Modelo
961.00
1
961.00
168.65
Pectina
961.00
1
961.00
168.65
Error
22.79
4
5.70
Total
983.79
5
CpMallows
136.12
p-valor
0.0002
0.0002
Regresión Lineal entre la Firmeza de la Batata empacada y diferentes porcentajes de Pectina
81.77
Firmeza
72.61
63.45
54.29
45.13
0.00
0.79
1.57
2.36
3.15
Pectina
Pruebas de hipótesis:
Pendiente (en regresión, típicamente nos interesa determinar si la pendiente es significativa):
Ho: 1  0 (No existe relación lineal entre las dos variables)
Ha: 1  0 (Hay relación lineal entre las variables)
Coeficientes de regresión y estadísticos asociados
Coef
Pectina
Est.
EE
LI(95%)
10.33 0.80
AGRO 5005 – CLAVE – Lab 13
8.12
LS(95%)
12.54
T
12.99
p-valor
0.0002
Page 4
(revisado_Oct 2015_LWB)
Probando la hipótesis usando el p-valor:
Como el p-valor es menor que nuestra alfa de 0.05, se rechaza la Ho; por lo tanto, hay evidencia de
que hay relación lineal entre las variables.
Probando la hipótesis comparando el T (observado o calculado) con t tabular (“crítico”):
La región de rechazo sería |tcalculado|> tα/2, glError=t0.025;4 = 2.776 (se usan los g.l. de error)
T (observado o calculado) cae en la región de rechazo (mucho mayor que t tabular); hay evidencia
para rechazar la hipótesis nula (o sea, hay una relación lineal de %pectina sobre la firmeza).
Haciendo los cálculos a mano tenemos:
𝒕𝒐𝒃𝒔 =
̂ 𝟏− 𝟎
𝜷
𝑺𝜺 /√𝑺𝒙𝒙
gl = n-2
̂ 𝑺
𝑺𝒚𝒚 − 𝜷
𝑺𝑪𝒓𝒆𝒔𝒊𝒅𝒖𝒂𝒍
𝒊 𝒙𝒚
= √𝑪𝑴𝑬𝒓𝒓𝒐𝒓 =
=
𝒏−𝟐
𝒏−𝟐
𝟐
(∑
𝒚
)
𝒊
𝑺𝒚𝒚 = ∑ 𝒚𝟐𝒊 −
𝒏−𝟐
𝑺𝒚𝒚 = 𝟗𝟖𝟑. 𝟕𝟗𝟑𝟑𝟑𝟑
𝑺𝟐𝜺 = √𝟓. 𝟕𝟕𝟓𝟖𝟑𝟑𝟐𝟓
𝑺𝟐𝜺
𝑺𝜺 = 𝟐. 𝟒𝟎𝟑𝟐𝟗𝟔𝟑𝟑
𝒕𝒐𝒃𝒔 = 𝟏𝟐. 𝟗𝟗
Por lo tanto hay evidencia de que hay relación lineal entre variables.
Finalmente, tenemos la opción de probar la hipótesis con una prueba de F, utilizando los cuadrados
medios del ANOVA:
Favor de notar que t 2  F : (12.99)2 = 168.74
Fobservado = CMregresión/ CMerror = 960.69/5.775 = 166.353 (no es exactamente el valor
que aparece en InfoStat debido al error de redondeo)
Ftabular con 1gl y 4 gl = 7.71
Fobs > Ftab; concluimos que hay evidencia para rechazar la Ho – hay evidencia de
una relación lineal)
g. ¿Es posible predecir la firmeza promedio que se obtendría usando 2% de pectina?, ¿y usando
6% de pectina? Si su respuesta es afirmativa, obtenga el valor predicho. De lo contrario,
justifique.
Sí, es posible predecir la firmeza para una concentración de pectina de 2%, puesto que este valor
se encuentra dentro de los valores de la variable.
Firmeza=48.33+10.33 (2)=69.59
No es posible predecir el valor de firmeza con una concentración de pectina del 6%, ya que sale
del rango de valores de x evaluados
AGRO 5005 – CLAVE – Lab 13
Page 5
(revisado_Oct 2015_LWB)
h. Construya un intervalo de confianza del 90% para 0. Interprete este intervalo en términos
del problema.
IC90%

: B0  t 
2
, glerror
S
X
OJO!!!!: Esta cantidad (el error
estándar del intercepto) puede ser
obtenido directamente de la salida de
InfoStat (en InfoStat se llama “E.E.”)
2
nS xx
𝟐𝟐. 𝟓
𝟒𝟖. 𝟗𝟑 ± 𝒕𝟎.𝟎𝟓,𝟒 √𝟓. 𝟕𝟕𝟓𝟖𝟑𝟑𝟐𝟓 √
𝟔(𝟗)
𝟐𝟐. 𝟓
𝟒𝟖. 𝟗𝟑 ± 𝟐. 𝟏𝟑𝟐 √𝟓. 𝟕𝟕𝟓𝟖𝟑𝟑𝟐𝟓 √
𝟔(𝟗)
Por ejemplo, aquí el E.E. del intercepto
es 1.54 (y el E.E. del pendiente es 0.80)
𝟒𝟖. 𝟗𝟑 ± 𝟑. 𝟑𝟎𝟕𝟒𝟏𝟔𝟔𝟎𝟕
(45.62 , 52.24)
Con una confianza de 0.90, el valor promedio de firmeza cuando no se agregue pectina estará
entre 45.62 y 52.24.
2. A efectos de estimar la productividad de un bosque, se desea estudiar la relación entre el área
basal de un árbol (x, en m2) y el volumen maderable del mismo (y, en m3). Se obtuvo una
muestra aleatoria de 12 árboles y para cada árbol se midió el área basal y el volumen maderable
luego de cortado.
Área
basal
Volumen
.3
.5
.4
.9
.7
.2
.6
.5
.8
.4
.8
.6
6
9
7
19
15
5
12
9
20
9
18
13
a. Utilizando InfoStat (Análisis de Correlación > Coeficientes de correlación), determine e
interprete el coeficiente de correlación lineal usando = 0.05.
Ho: ρ = 0 (no hay una asociación lineal entre X y Y)
Ha: ρ ≠ 0 (hay una asociación lineal entre X y Y)
r
AGRO 5005 – CLAVE – Lab 13
S XY
11.917

 0.97
S XX SYY
0.509(295.667)
Page 6
(revisado_Oct 2015_LWB)
No importa el orden de entrar las
variables
Coeficientes de correlación
Correlación de Pearson: coeficientes\probabilidades
Volumen_m3
Area Basal_m2
Volumen_m3
1.00
1.5E-07
Area Basal_m2
0.97
1.00
0.97 es el coeficiente de correlación. El cuadrado del coeficiente de
correlación se llama “el coeficiente de determinación (R2). El tamaño de
R2 es una indicación del ajuste del modelo de regresión. Es igual al
CMregressión/CMtotal. Valores cerca de 1.0 indican un “buen ajuste”
1.5E-07 (=0.00000015) es el p-valor del coeficiente de correlación. En
este caso, rechazamos la Ho porque es mucho menor que nuestra alfa.
b. Utilice InfoStat para conducir un análisis de regresión lineal. Interprete (si fuese posible) los
estimadores del intercepto y de la pendiente en términos de este problema. Formule y pruebe
las hipótesis de interés usando =.01. Indique sus conclusiones.
AGRO 5005 – CLAVE – Lab 13
Page 7
(revisado_Oct 2015_LWB)
Análisis de regresión lineal
Variable N
R² R² Aj ECMP AIC BIC
Volumen_m3 12
0.94 0.94 2.60 44.07 45.52
Coeficientes de regresión y estadísticos asociados
Coef
CpMallows
C
Const
A
Area Basal_m2
152.32
Est.
E.E.
-1.23 1.08
23.40 1.81
LI(95%)
-3.64
19.36
LS(95%)
1.17
27.45
Cuadro de Análisis de la Varianza (SC tipo III)
F.V.
SC
gl
CM
F
Modelo
278.90
1
278.90
166.35
Area Basal_m2
278.90
1
278.90
166.35
Error
16.77
10
1.68
Total
295.67
11
T
p-valor
-1.14 0.2798
12.90 <0.0001
p-valor
<0.0001
<0.0001
Ecuación lineal estimada

 

Y  B0  B1 x , donde Y es el volumen maderable (m3), x es el área basal (m2)
Volumen maderable= -1.23 + 23.40 Área basal
AGRO 5005 – CLAVE – Lab 13
Page 8
(revisado_Oct 2015_LWB)
Relación entre Volumen Maderable y Area Basal
20.75
Volumen_m3
16.22
11.69
7.16
2.63
0.17
0.36
0.55
0.74
0.94
Area Basal_m2
Ho: 1  0 (No existe relación lineal entre las dos variables)
Ha: 1  0 (Hay relación lineal entre las variables)
Coeficientes de regresión y estadísticos asociados
Coef
Área basal
Est.
EE
23.40 1.81
LI(95%)
19.36
LS(95%)
27.45
T
p-valor
12.90 <0.0001
Como el p-valor es menor que 0.01, se rechaza la Ho; por lo tanto, hay evidencia de que hay
relación lineal entre las variables.
Con el estadístico de prueba sería:
𝒕𝒐𝒃𝒔 =
̂ 𝟏− 𝟎
𝜷
𝑺𝜺 /√𝑺𝒙𝒙
=
𝟐𝟑.𝟒
𝟏.𝟐𝟗𝟔𝟕𝟔𝟓𝟐𝟏𝟐/√𝟎.𝟓𝟎𝟗𝟏𝟔𝟔
= 𝟏𝟐. 𝟗
La región de rechazo sería |tcalculado|> tα/2, glError=t0.005;10=3.169
Por lo tanto hay evidencia de que hay relación lineal entre variables.

El valor de B1 significa que por cada unidad (m2) de área basal que un árbol aumente se está
incrementando 23.40 m3 de volumen maderable del árbol. Esto es equivalente a decir, en valores
más cercanos a los estudiados, que al aumentar 0.1 m2 de área basal se incrementa el volumen
maderable del árbol en 2.34 m3.

El valor del intercepto ( B0 ) no se interpreta ni se prueba, puesto que no es posible registrar
valores de área basal (x) cero.
3. En el archivo de InfoStat reglin (que lo encontrará en Program Files>InfoStat>Datos) se
encuentran datos que estudian la relación entre el pH del medio de cultivo y la biomasa
producida (en g).
a. Utilice InfoStat para graficar los datos.
AGRO 5005 – CLAVE – Lab 13
Page 9
(revisado_Oct 2015_LWB)
Producción de Biomasa según el pH
1030
Biomasa
905
780
655
530
3
4
5
6
7
pH
b. Formule y pruebe las hipótesis apropiadas de regresión lineal.
Análisis de regresión lineal
Variable
Biomasa
N
45
R² R² Aj
0.95 0.95
ECMP
909.73
AIC
434.87
BIC
440.29
Coeficientes de regresión y estadísticos asociados
Coef
const
pH
Est.
313.95
95.56
E.E.
15.87
3.35
LI(95%)
281.94
88.80
LS(95%)
345.96
102.32
T
19.78
28.51
p-valor
<0.0001
<0.0001
Cuadro de Análisis de la Varianza (SC tipo III)
F.V.
SC
gl
CM
F
p-valor
Modelo
685876.59 1
685876.59 812.81
<0.0001
pH
685876.59 1
685876.59 812.81
<0.0001
Error
36284.63 43
843.83
Total
722161.23 44
AGRO 5005 – CLAVE – Lab 13
Page 10
(revisado_Oct 2015_LWB)
Regresión Lineal entre la Biomasa y el pH
1014.74
Biomasa
894.25
773.77
653.29
532.80
2.80
3.90
5.00
6.10
7.20
pH
Pendiente:
Ho: 1  0 (No existe relación lineal entre las dos variables)
Ha: 1  0 (Hay relación lineal entre las variables)
Coeficientes de regresión y estadísticos asociados
Coef Est. EE LI(95%)
const 313.95 15.87 281.94
pH
95.56 3.35
88.80
LS(95%)
345.96
102.32
T
p-valor
19.78 <0.0001
28.51 <0.0001
Como el p-valor es menor que 0.05, se rechaza el Ho; por lo tanto, hay evidencia de que hay
relación lineal entre las variables.
Si existe un efecto lineal significativo de pH del medio sobre la biomasa producida, estime la
ecuación que mejor describe esta relación.

 

Y  B0  B1 x donde x=pH, Y =Biomasa
Biomasa=313.95+95.56pH
d. Interprete, si fuese posible, los estimadores del intercepto y de la pendiente en términos de este
problema.

El valor de B0 no es interpretado puesto que no existe valores de pH igual a 0.
AGRO 5005 – CLAVE – Lab 13
Page 11
(revisado_Oct 2015_LWB)

El valor de B1 está indicando que por cada unidad de pH que se aumente, hay un incremento
promedio de biomasa de 95.56.
e. Construya un intervalo de confianza del 99% para β1.
α = 0.01 α/2 = 0.005
gl = n -2 = 43

IC99% : B1  t 
S
, glerror
S xx
29.048
95.56  t0.005,43
75.11
95.56  2.695(3.35)
95.56  9.028
(104.59;86.53)
2
4. Generalmente se considera que las personas más altas son mejores jugadores de baloncesto
porque son más capaces de introducir la bola en la canasta. Los datos que aparecen en la tabla de
basquetbol (en la página del curso) muestran las alturas de 25 atletas que no son jugadores de
baloncesto y el número de bolas que pudieron colocar en un período de 60 segundos.
a. Conduzca un análisis de regresión lineal que permita corroborar o no esta afirmación.
b. Interprete (si fuese posible) los estimadores del intercepto y de la pendiente en términos de este
problema.
c. Formule y pruebe las hipótesis de interés usando α=.01. Indique sus conclusiones.
d. Prediga, si es posible, la cantidad de bolas que colocaría un jugador de 60” de altura y uno de 77” de
altura.
Análisis de regresión lineal
Variable
Cestas
N
25
R²
0.94
R² Aj ECMP
0.93 0.81
AIC
BIC
63.95 67.61
Coeficientes de regresión y estadísticos asociados
Coef
Est.
CpMallows
const
-71.45
Altura_in
1.21
322.02
E.E.
LI(95%)
LS(95%)
4.83
0.07
-81.44
1.07
-61.47
1.35
Cuadro de Análisis de la Varianza (SC tipo III)
F.V.
SC
gl
CM
F
Modelo
216.49
1
216.49
334.93
Altura_in
216.49
1
216.49
334.93
AGRO 5005 – CLAVE – Lab 13
T
-14.80
18.30
p-valor
<0.0001
<0.0001
p-valor
<0.0001
<0.0001
Page 12
(revisado_Oct 2015_LWB)
Error
Total
14.87
231.36
23
24
0.65

 

donde x =Altura_in, Y = Cestas
Y  B0  B1 x
Cestas = -71.45 + 1.21 (Altura_in)
Cestasen un minuto según altura de personas no atletas
25
Cestas
22
19
16
13
10
68
70
72
74
76
78
80
Altura (")
Esta gráfica indica que existe una relación lineal entre la altura de una persona no atleta y
la cantidad de cestas que acierta, corroborando la afirmación establecida en el enunciado.
La prueba de hipótesis Ha: 1 ≠ 0 (hay relación lineal entre las variables) y 1 = 0 (no hay
relación lineal entre las variables), confirma la afirmación.
Como el p-valor es menor que 0.01, se rechaza la Ho; por lo tanto, hay evidencia de que hay
relación lineal entre las variables.
Con el estadístico de prueba sería:
𝒕𝒐𝒃𝒔 =
̂ 𝟏− 𝟎
𝜷
=
𝑺𝜺 /√𝑺𝒙𝒙
𝑺𝒙𝒙 = ∑ 𝒙𝟐𝒊 −
𝟏.𝟐𝟏
𝟎.𝟖𝟎𝟏𝟑𝟓𝟖/√𝟏𝟒𝟖
= 𝟏𝟖. 𝟑𝟔
Donde:
𝟐
(∑ 𝒙𝒊 )
𝒏
= 𝟏𝟒𝟖
𝟐
𝑺𝒚𝒚 =
∑ 𝒚𝟐𝒊
(∑ 𝒚𝒊 )
−
= 𝟐𝟑𝟏. 𝟑𝟔
𝒏−𝟐
𝑺𝒙𝒚 = ∑ 𝒙𝒊 𝒚𝒊 −
∑ 𝒙 𝒊 ∑ 𝒚𝒊
= 𝟏𝟕𝟗
𝒏
AGRO 5005 – CLAVE – Lab 13
Page 13
(revisado_Oct 2015_LWB)
𝑺𝟐𝜺
̂ 𝑺
𝑺𝒚𝒚 − 𝜷
𝑺𝑪𝒓𝒆𝒔𝒊𝒅𝒖𝒂𝒍
𝟏 𝒙𝒚
=
=
= 𝟎. 𝟔𝟒𝟐𝟏𝟕
𝒏−𝟐
𝒏−𝟐
𝑺𝜺 = 𝟎. 𝟖𝟎𝟏𝟑𝟓𝟖
La región de rechazo sería |tcalculado|> tα/2, glError=t0.005;23=2.808
Por lo tanto hay evidencia de que hay relación lineal entre variables.

El valor de B1 significa que por cada unidad (in) de aumento en altura de la persona, se
está incrementando en 1.21 el número de cestas que una persona puede acertar.El valor

del intercepto ( B0 ) no se interpreta ni se prueba, puesto que no es posible registrar valores
de altura igual a cero (las alturas de las personas estudiadas están entre 69 y 79).
Predicción:
Cestas = -71.45 + 1.21 (Altura_in)
Rango de alturas en los datos: 69 in a 79 in
No es posible calcular el número de cestas para una persona de 60 in de estatura, puesto que
este valor está por fuera de los calculados para la ecuación.
Para una persona de 77 in, la predicción de cestas es la siguiente:
Cestas = -71.45 + 1.21 (77) = 21.72 (aproximadamente 22)
AGRO 5005 – CLAVE – Lab 13
Page 14