Transparencias 7
Anuncio

Estadı́stica y sus aplicaciones en Ciencias Sociales
7. El modelo de regresión simple
Facultad de Ciencias Sociales - UdelaR
Índice
7.1 Introducción
7.2 Análisis de regresión
7.3 El Modelo de Regresión Lineal Simple
7.4 Métodos de estimación
7.5 Propiedades algebraicas de los estimadores
7.1 Introducción: ¿Qué es la econometrı́a?
I
La econometrı́a es la ciencia que aplica métodos matemáticos
y estadı́sticos de análisis de datos con el objetivo de dotar de
una base empı́rica a una teorı́a social (en particular
económica).
I
La metodologı́a aplicada en econometrı́a no ha sido utilizada
exclusivamente por la ciencia económica.
I
El principal problema que tienen las ciencias sociales es que la
mayor parte de los datos son no experimentales, siendo mucho
más compleja su recolección.
I
Metodologı́a:
1. Contar con una teorı́a social (o económica) que requiera
validez y su equivalente modelo econométrico.
2. Tener datos de la realidad que permitan estimar dicho modelo
para contrastarlo.
3. Realizar inferencia o pruebas de hipótesis que nos permitan
determinar si nuestros resultados son estadı́sticamente
significativos.
I
Si la respuesta es afirmativa podremos realizar
recomendaciones de polı́ticas asociadas.
Metodologı́a aplicada
Teoría Social (Económica)
Modelo Econométrico
Ecuación
Datos
Supuestos
Estimación
Inferencia y prueba de hipótesis
Sí
Predicciones y recomendaciones de política
No
7.2 Análisis de regresión: ¿Qué es una regresión?
I
En una regresión buscamos un modelo para representar la
dependencia de una variable respuesta, y , respecto a otra
variable explicativa, x.
I
El objeto es el de estimar el promedio poblacional de la
variable dependiente condicionando los valores de la variable
explicativa.
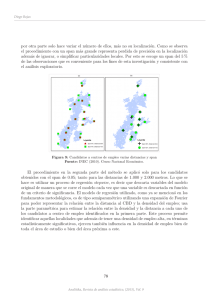
Ingresos y educación
3000
2500
Salario por hora
2000
1500
1000
500
0
6
7
8
9
10
11
Años de educación formal
12
13
14
15
I
Para cada año de educación formal tenemos un rango o
distribución de salario por hora y el promedio del salario
aumenta a medida que se incrementan los años de educación.
I
Si trazamos una recta que tome los valores promedio de
salario para cada año de educación observamos este hecho.
I
La recta corresponde a la recta de regresión y nos permite
predecir para cada año de educación formal el salario
promedio correspondiente.
Regresión vs. Causalidad
I
La regresión es una relación estadı́stica y no implica
causalidad a priori.
I
Una relación estadı́stica no puede por sı́ misma implicar en
forma lógica una causalidad.
Regresión vs. Correlación
I
El análisis de correlación está estrechamente ligado al de
regresión, aunque conceptualmente son cosas muy diferentes.
Correlación:
I
mide el grado de asociación lineal entre dos variables,
I
las variables son tomadas de forma simétrica.
Regresión:
I
estimamos el valor promedio de una variable dependiente , y ,
dada una variable explicativa, x,
I
las variables son tratadas de forma asimétrica: y es la variable
aleatoria de interés y x es la variable aleatoria que puede
influir en y .
Precauciones
I
El coeficiente de correlación mide una relación lineal
I
Correlación no implica causalidad, es sólo una relación
estadı́stica
I
Correlación puede indicar una relación espuria.
El análisis de correlación puede ayudarnos a determinar la ecuación
de estimación y si ésta realmente describe su verdadero
comportamiento.
7.3 El Modelo de regresión lineal simple
I
Sean y y x dos variables que representan una población.
I
Estamos interesados en explicar y en términos de x o estudiar
cómo varı́a y ante cambios en x.
I
Al crear un modelo que “explique y en términos de x”
tenemos varios problemas:
1. Dado que no existe una relación exacta entre dos variables:
¿cómo tomamos en cuenta otros factores que alteran a y ?
2. ¿Cuál es la relación funcional entre y y x?
3. ¿Cómo nos aseguramos de capturar una relación ceteris
paribus entre y y x (si eso queremos)?
7.3.1 El MRL
Consideremos la siguiente ecuación que relaciona y con x de la
siguiente forma:
y = β0 + β1 x + u
(1)
Esta es una representación del modelo de regresión lineal simple,
de dos variables o bivariada.
I
y se la denomina variable dependiente, explicada, de
respuesta, predicha, o regresando.
I
x se la denomina variable independiente, explicativa, de
control, predictora, o regresor.
I
La variable u, denominada término de error o perturbación de
la relación, representa los factores, aparte de x, que influyen
en y .
I
β0 es la magnitud que no es explicada por la variable
dependiente
I
β1 es el parámetro de la pendiente de la relación entre x e y si
se mantienen fijos en u los otros factores, o sea ∆u = 0:
∆y = β1 ∆x
si
∆u = 0
(2)
I
β1 también muestra la dependencia lineal (o correlación) entre
la variable dependiente e independiente.
I
Un cambio de una unidad en x tiene el mismo efecto en y
cualquiera que sea el valor inicial de x.
Ejemplo: Salarios y educación
I
Este modelo relaciona el salario de una persona con la
educación observada y otros factores no observados.
salario = β0 + β1 educ + u
I
salario se mide en pesos por hora y educ corresponde a la
cantidad de años de educación formal.
I
β1 mide el cambio en el salario por hora cuando se introduce
un año de formación adicional, manteniendo todos los demás
factores fijos.
I
Entre los demás factores se incluyen la experiencia en el
trabajo, la habilidad innata, la antigüedad en el empleo
actual, etc.
7.3.2 Supuesto fundamental del MRL
I
Para poder obtener conclusiones de como afecta x a y
debemos establecer algún supuesto de cómo se relacionan u y
x.
I
Dado que u y x son variables aleatorias, podemos definir la
distribución condicional de u dado cualquier valor de x.
I
En particular, para cualquier x, podemos obtener el valor
esperado (o promedio) de u.
I
El supuesto crucial es que el valor promedio de u no depende
de x (media condicional cero).
E (u|x) = 0
(3)
Este supuesto significa que para cualquier x, el promedio de los
factores inobservables es el mismo e igual al promedio de u para
toda la población.
I
Ejemplo salario y educ: si u es la habilidad innata, que se
cumpla (3) implica que el nivel de habilidad medio de la
población es el mismo para todos los niveles educativos. Si
pensamos que la habilidad media de las personas aumenta con
los años de educación (3) es falso.
I
Una consecuencia de este supuesto es:
E (y |x) = E (β0 + β1 x + u|x) = β0 + β1 x
I
Como observamos en el gráfico de la página 7 el salario por
hora es diferente para individuos con el mismo nivel educativo.
I
También observamos que en promedio, el salario se
incrementa con educ.
I
La unión de los valores esperados del salario condicionados a
los años de educación representa la función de regresión
poblacional (FRP):
E (y |x) = β0 + β1 x
I
El término poblacional refiere a que estamos trabajando con
toda la población.
I
La FRP la vamos a conocer en casos excepcionales, ya que
rara vez vamos a tener datos de toda la población.
I
La FRP es una función lineal de las x
E(y|x) = β0 + β1x
.
u4 {
y
y4
y3
y2
y1
u {.
2
.} u1
x1
I
.} u3
x2
x3
x4
x
La linealidad significa que un aumento de una unidad en x
cambia el valor esperado de y en la cantidad β1 .
7.3.3 Consecuencias del supuesto fundamental E (u|x) = 0
E (u) = 0
I
se obtiene de integrar E (u|x) para todo el recorrido de x,
como para todo valor de x es igual a cero, integrar 0 arroja el
valor esperado de u igual a cero.
Cov (u, x) = E [u − E (u)]E [x − E (x)] = E (ux) = 0
I
(4)
dado que el valor esperado de u no depende de x, no están
correlacionadas y su covarianza es cero.
(5)
7.4 Métodos de estimación
Los métodos que tenemos para estimar cómo influye una variable
dependiente sobre una independiente suelen ser:
7.4.1 Método de Momentos
7.4.2 Mı́nimos Cuadrados Ordinarios
Existen otros métodos de estimación que exceden los objetivos de
este curso.
7.4.1 Método de Momentos
La estimación de los parámetros del modelo a partir del método de
momentos consiste en utilizar los momentos correspondientes a los
errores:
E (u) = E [y − β0 − β1 x] = 0
E (xu) = E [x(y − β0 − β1 x)] = 0
I
Estas ecuaciones implican dos restricciones en la distribución
conjunta de x e y en la población.
I
Dado que hay dos parámetros desconocidos (β0 , β1 ) y dos
ecuaciones que cumplen con la condición podemos
identificarlos.
I
Consideremos una muestra de tamaño n: {yi , xi } con
i = 1, 2, ..., n, extraı́da aleatoriamente de la población.
I
Buscamos estimar los parámetros β0 y β1 que provienen del
MRL, por lo que podemos establecer:
yi = β0 + β1 xi + ui
I
Dada la muestra de datos, elegimos los valores estimados de
βˆ0 y βˆ1 para resolver las contrapartidas muestrales:
n
1X
[yi − βb0 − βˆ1 xi ] = 0
n
i=1
n
1X
n
i=1
[xi (yi − βb0 − βˆ1 xi )] = 0
I
Desarrollando la primera ecuación se obtiene:
n
n
n
1X
βb0 X
βb1 X
yi −
1−
xi = 0
n
n
n
i=1
I
I
i
Que se puede escribir como:
y − βb0 − βb1 x = 0
i
(6)
Una vez que tenemos el estimador de la pendiente βb1 es fácil
obtener el de la ordenada al origen βb0 , dados los promedios
muestrales y y x.
βb0 = y − βb1 x
(7)
I
Sustituyendo (7) en la segunda ecuación de las contrapartidas
muestrales, se obtiene:
n
1X
xi (yi − (y − βb1 x) − βb1 xi ) = 0
n
i=1
I
lo que reordenando da:
n
X
i=1
xi (yi − y ) = βb1
n
X
i=1
xi (xi − x)
I
Dado que:
n
n
X
X
yi − nxy = nxy − nxy = 0
(xyi − xy ) = x
i=1
i=1
I
y que:
n
X
(xxi − x 2 ) = x
Podemos sumar cero en la primer sumatoria:
n
X
xi (yi − y ) =
i=1
I
xi − nx 2 = nx 2 − nx 2 = 0
i=1
i=1
I
n
X
n
X
(xi yi − xi y − xyi + xy ) =
i=1
n
X
(xi − x) (yi − y )
i=1
Y sumar cero a la segunda sumatoria:
n
X
i=1
xi (xi − x) =
n
X
i=1
n
X
(xi − x)2
xi2 − xi x − xi x + x 2 =
i=1
Estimador de la pendiente
I
El estimador de la pendiente es:
Pn
(xi − x) (yi − y )
b
β1 = i=1
Pn
2
i=1 (xi − x)
(8)
I
El estimador de la pendiente es igual a la covarianza muestral
entre x e y , dividida por la varianza muestral de las x
(siempre positiva).
I
b
Si la covarianza
Pnentre x e y2 es positiva, β1 será positivo. Se
requiere que i=1 (xi − x) > 0
I
I
La “lı́nea de regresión” o función de regresión muestral
(FRM) es la recta ajustada yb = βb0 + βb1 x.
En el gráfico se representa con los puntos muestrales y los
residuos. Diferentes muestras generarán diferentes rectas
estimadas.
.
y4
û4 {
y = β 0 + β1 x
y3
y2
y1
û2 { .
.} û1
x1
I
.} û3
x2
x3
x4
x
El objetivo del análisis de regresión es estimar la FRP en base
a la FRM.
7.4.2 Mı́nimos cuadrados ordinarios
I
Podemos pensar a cada observación como compuesta de un
parte explicada y una parte inexplicada:
yi = ybi + ubi
I
Los MCO descomponen cada observación i en dos partes, un
valor ajustado ybi y un residuo ubi . El residuo ubi es
conceptualmente diferente del error.
I
El residuo de la observación i lo podemos escribir como:
ubi = yi − ybi = yi − βb0 − βb1 xi
I
Si queremos que la FRM sea lo más cercana posible a la FRP,
debemos tratar de elegir los coeficientes de regresión de tal
forma que los residuos sean lo más pequeños posibles.
I
De acuerdo a esto un criterio para escoger la FRM podrı́a ser
la de minimizar la suma de los residuos al cuadrado:
n
X
i=1
ubi2
n
n
X
X
2
=
(yi − ybi ) =
(yi − βb0 − βb1 xi )2
i=1
(9)
i=1
I
Se realiza la minimización de los cudarados para penalizar más
a los errores de las observaciones que se desvı́an de la FRP.
I
De esta forma, elP
método de MCO elige β̂0 y β̂1 tal que para
la muestra dada ni=1 ubi2 sea lo más pequeña posible.
I
Para resolver el problema de MCO se minimiza la ecuación
(9), obteniéndose las siguientes condiciones de primer orden:
∂
Pn
∂
∂ βb0
Pn
bi2
i=1 u
bi2
i=1 u
∂ βb1
= −2
= −2
n
X
[yi − βb0 − βb1 xi ] = 0
i=1
n
X
[xi (yi − βb0 − βˆ1 xi )] = 0
i=1
I
Que son las mismas ecuaciones que obtenı́amos del método de
momentos, por lo que los estimadores de la pendiente y el
intercepto son los mismos que por el método anterior.
I
Por lo tanto:
MCO
βb0
Método de Momentos
= βb0
MCO
βb1
Método de Momentos
= βb1
Ejemplo: Ingreso y consumo
Intentaremos estimar la siguiente relación entre consumo privado e
ingreso disponible:
C = β0 + β1 YD + u
Años
1970
1971
1972
1973
1974
1975
1976
1977
1978
1979
Promedio:
Consumo
privado (Y )
672.1
696.8
737.1
767.9
762.8
779.4
823.1
864.3
903.2
927.6
793.4
Ingreso
disponible (X )
751.6
779.2
810.3
864.7
857.5
874.9
906.8
942.9
988.8
1015.7
879.2
Ejemplo: se pide
1. Estimar la relación entre C e YD empleando MCO, es decir,
obtener los valores estimados del término constante y de la
pendiente.
P1979
i=1970 (xi − x)(yi − y )
βˆ1 =
P1979
2
i=1970 (xi − x)
βˆ0 = y − βˆ1 x
2. Comentar la dirección de la relación. ¿El término constante se
presta a una interpretación útil en este caso? Explicar la
respuesta.
3. Si el ingreso disponible asciende a 970 dólares en 1980, ¿cuál
será el consumo proyectado?
4. Calcular los valores ajustados y los residuos para cada
observación y comprobar que los residuos suman
(aproximadamente) cero.
Interpretación de la regresión
I
Cuando el ingreso disponible es 0, el consumo es menor a cero.
Esto no tiene sentido, lo que sucede es que esta muestra es
muy pequeña y la ecuación de regresión no tiene muy buenos
resultados para niveles de ingreso disponible muy bajos.
I
El valor estimado de la pendiente indica que con un peso más
de ingreso disponible se incrementa en 0.98 pesos el consumo.
I
¿Cuánto es el consumo predicho si el ingreso disponible se
duplica?
4b
y = βb1 4x ⇒ 4Cb = 0,9793 × 2 = 1,959
Efecto de la muestra en la estimación de los parámetros
1000
950
y = 0.9793x - 67.581
900
Consumo privado
y = 0.8632x + 39.12
850
FRM2
800
FRM1
Lineal (FRM2)
750
Lineal (FRM1)
700
650
600
720
770
820
870
920
Ingreso disponible
970
1020
1070
7.5 Propiedades algebraicas de los estimadores MCO
I
La suma y la media muestral de los residuos MCO es nula:
n
X
ubi = 0
(10)
i=1
I
La covarianza muestral entre los regresores y los residuos
MCO es nula:
n
X
xi ubi = 0
(11)
i=1
I
El punto (y , x) siempre pasa por la regresión MCO.
yb = βb0 + βb1 x = yb
(12)
7.5.1 Definiciones: Medidas de variación de la variable
dependiente
1. Suma de los cuadrados totales:
SCT ≡
n
X
(yi − y )2
(13)
i=1
2. Suma explicada de los cuadrados:
SEC ≡
n
X
(ybi − y )2
(14)
i=1
3. Suma de los cuadrados de los residuos:
SCR ≡
n
X
i=1
2
ubi =
n
X
i=1
(yi − yb)2
(15)
La SCT la podemos expresar como:
SCT
=
n
X
(yi − y )2
i=1
=
n
X
[(yi − ybi ) + (ybi − y )]2
i=1
=
=
n
X
i=1
n
X
[ubi + (ybi − y )]2
ubi 2 +2
n
X
ubi (ybi − y ) +
i=1
|i=1{z }
= SCR + 2
n
X
n
X
(ybi − y )2
|i=1 {z
ubi (ybi −y ) +
SEC
i=1
|
= SCR +
SCT
= SCR + SEC
{z
0
}
+
SEC
}
7.5.2 Bondad de ajuste
I
¿Qué tan bien se ajusta a los datos de nuestra muestra la
lı́nea de regresión muestral?
I
Se puede calcular la fracción de la suma de cuadrados total
(SCT) explicada por el modelo, a la que se llama R-cuadrado
de la regresión o coeficiente de determinación:
R2 =
I
SCR
SEC
=1−
SCT
SCT
Se interpreta como la fracción o porcentaje de la variación
muestral de y que es explicada por x.
Comentarios sobre R 2
I
R 2 ∈ [0, 1]
I
I
I
Si R 2 = 0 es porque β1 es cero, menos el término constante, la
FRM va a ser una recta horizontal. En este caso el valor
predicho de y es y , ya que desviaciones de x respecto a su
media no se traducen en una predicción diferente para y . x no
tiene poder explicativo en y .
Si R 2 = 1 ocurre si los valores de x y y están todos en el
mismo hiperplano (en una lı́nea recta) por lo que los residuos
son cero.
Es posible demostrar que R2 es igual al cuadrado del
coeficiente de correlación muestral entre yi y ybi . De aquı́
procede el término.
I
Obtener un R2 elevado no implica que el modelo es apropiado
ni que las estimaciones de los coeficientes son buenas.
I
Obtener un R2 bajo no implica que el modelo es inapropiado
ni que las estimaciones de los coeficientes son malas.
I
Depende de la construcción de nuestro modelo y de las
preguntas que deseamos responder con él.
7.5.3 Valor esperado y varianza de los estimadores MCO
Supuesto RLS1 (linealidad de los parámetros)
I
Supongamos que el modelo en la población es lineal en los
parámetros como en y = β0 + β1 x + u
Supuesto RLS2 (muestreo aleatorio)
I
Supongamos una muestra aleatoria de tamaño n,
{(yi , xi ), i = 1, 2, ...n}, del modelo poblacional. Entonces se
puede escribir el modelo como:
yi = β0 + β1 xi + ui ,
i = 1, 2, ...n
Supuesto RLS3 (Media condicionada nula)
I
Supongamos E (u|x) = 0 y por tanto E (ui |xi ) = 0.
Supuesto RLS4 (Variación muestral de la variable independiente)
I
Supongamos que hay variación en las xi (no son todas iguales
a una constante).
Comentario:
I
Los estimadores MCO son funciones de las observaciones xi ,
yi . Las propiedades estadı́sticas de los estimadores de MCO
son condicionales a los valores muestrales de las xi . Es como
tratar las xi como fijas en muestras repetidas.
I
La posibilidad de muestras repetidas no es muy realista en los
contextos no experimentales. Consecuencia: es necesario
prestar particular atención a la posible correlación entre las x
y las u y a las razones por las que esto puede suceder.
Insesgamiento: E (βbi ) = βi
E (βb1 ) = β1
E (βb0 ) = β0
I
El condicionamiento en los valores muestrales de la variable
independiente permite tomar a las funciones de las xi como no
aleatorias.
I
Los estimadores MCO de los parámetros β1 y β0 son entonces
insesgados.
I
Recordar que insesgamiento es una descripción del estimador
– en cada muestra podemos estar “cerca” o “lejos” del
parámetro verdadero.
Demostración insesgamiento para β1
Sabemos que:
Pn
(x − x)(yi − y )
i=1
b
Pn i
β1 =
(xi − x)2
Pn i=1
(xi − x)yi
= Pi=1
n
(xi − x)2
Pni=1
i − x)(β0 + β1 xi + ui )
i=1 (xP
=
n
2
i=1 (xi − x)
Pn
P
P
β0 i=1 (xi − x) + β1 ni=1 (xi − x)xi + ni=1 (xi − x)ui
Pn
=
(xi − x)2
Pni=1
Pn
β1 i=1 (xi − x)2
(xi − x)ui
β0 × 0
= Pn
+ Pn
+ Pi=1
n
2
2
2
(xi − x)
(xi − x)
i=1 (xi − x)
| i=1 {z
} | i=1 {z
}
Pn
(xi − x)ui
=
0
+
β1
+ Pi=1
n
2
i=1 (xi − x)
Por lo tanto:
Pn
xu −
i=1
Pni i
i=1 (xi
βb1 = β1 +
P
x ni=1 ui
− x)2
(16)
Tomando valor esperado, condicional en las observaciones:
Pn
E (βb1 |x) = E (β1 |x) +E
| {z }
=
β1
+
P
xi ui − x ni=1 ui
i=1
Pn
|x
2
i=1 (xi − x)
P
P
E ( ni=1 xi ui | x)
E ( ni=1 ui
Pn
P
−x n
2
i=1 (xi − x)
i=1 (xi −
|
=
β1
=
β1
+
{z
0
Es posible demostrar que E (βb0 |x) = β0
} |
+
{z
0
| x)
x)2
}
Comentarios sobre el insesgamiento
I
El insesgamiento es una caracterı́stica de las distribuciones
muestrales de βˆ1 y βˆ0 , que no dice nada sobre el valor
estimado que obtenemos para una muestra determinada. Si la
muestra que obtenemos es “tı́pica”, el valor estimado se
“aproxima” al valor poblacional.
I
Si el RLS3 no se cumple, obtendremos estimadores sesgados
de los parámetros poblacionales.
I
Las estimaciones sesgadas nos podrı́an llevar a
recomendaciones de polı́tica que no son correctas.
Varianza de los estimadores MCO
I
Sabemos que la distribución en el muestreo de nuestro
estimador está centrada en el parámetro. Quisiéramos saber
qué tan dispersa es ésta distribución.
I
Supuesto RLS5 (Homoscedasticidad)
Var (u|x) = E [u − E (u)|x]2
= E [u 2 |x]
= σ2
I
Este supuesto establece que la variación alrededor de la recta
de regresión es la misma para todos los valores de x. Esto
implica que la función de densidad del término de error u es la
misma.
Caso homoscedástico: Var (u | x) no depende de x
y
f(y|x)
.
x1
x2
. E(y|x) = β + β x
0
1
Varianza muestral de βb0 y βb1
I
Se puede demostrar que:
σ2
σ2
=
2
nVar (x)
i=1 (xi − x)
P
P
σ2 n x 2
σ2 n x 2
Var (βb0 |x) = Pn i=1 i 2 = 2 i=1 i
n i=1 (xi − x)
n Var (x)
Var (βb1 |x) = Pn
(17)
(18)
Varianza muestral del error
I
No conocemos la varianza del error, σ 2 , ya que no observamos
los errores, ui , sino los residuos, ubi .
I
Residuos y errores son diferentes:
ui
ubi
= yi − β0 − β1 xi
= yi − βb0 − βb1 xi
I
Los errores lo obtenemos de los parámetros poblacionales y
por tanto, nunca son observables.
I
Los residuos se obtienen de los parámetros muestrales.
I
Con los residuos es posible realizar una estimación de la
varianza del error.
ubi = yi − ybi = ui + β0 + β1 xi − βb0 − βb1 xi
I
Reordenando obtenemos:
ubi − ui = (βb0 − β0 ) − (βb1 − β1 )xi
I
Si bien el valor esperado de la diferencia entre error y residuo
es cero, no ocurre lo mismo con la diferencia simple.
I
Como E (u 2 ) = σ 2 , es natural intentar
σ 2 a partir de
Pnestimar
2
la suma de los residuos al cuadrado, i=1 ubi .
I
Un estimador de σ 2 serı́a:
2
σ
b =
Pn
2
i=1 ui
n
I
El problema es que no observamos ui , sino que lo debemos
estimar con ubi .
I
Es posible demostrar que el estimador insesgado de σ 2 es:
Pn
ubi 2
σ
b2 = i=1
(19)
n−2
Estimación de la varianza del error
I
El estimador insesgado de σ 2 no es simplemente el promedio
de los residuos al cuadrado, sino que su denominador está
“corregido por los grados de libertad”.
I
El P
denominador no es n sino (n − 2) porque
E ( ni=1 ubi2 ) = (n − 2)σ 2 .
I
La división por (n − 2) lleva a que σ
b2 sea insesgado para σ 2 .
√
b2 .
El estimador natural de σ es σ
b= σ
I