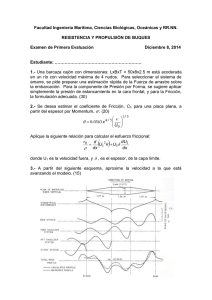
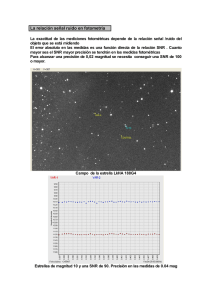
ω ϕ = ω μ η η

Control Intermedio de Teoría de la Comunicación
7 de Abril de 2010
1.5. Escribir la forma de la señal DBL y su envolvente compleja, ambas a la
entrada y salida del canal, especificando los valores de los parámetros. (1 pto.)
Para una señal paso banda genérica (la señal que se transmite al canal en el ejercicio es un
caso particular), la envolvente compleja y (t ) y se define de la siguiente manera:
La relación entre estas señales, todas ellas con características paso-bajo (excepto la propia
señal y(t)) es:
Para
el
caso
particular
de
nuestra
señal
DBL y (t ) = Ac x(t ) cos ωc t
y
px=0.5,
2
py=0.5W=Ac px/2 (→Ac=√2 V),
ϕ (t ) = 0, r (t ) = Ac x(t )
yI (t ) = Ac x (t ),
yQ (t ) = 0,
y (t ) = yI (t ) = r (t ) = Ac x(t )
La salida del canal, si Bx<=8KHz y fc=1018KHz, es
yc (t ) = M o Ac x(t − t g ) cos(ωc (t − t p ))
con M0=10-80/20 =10-4, t g =
−1 d < H c ( f )
2π
df
f = fc
= 10μ s de acuerdo a las gráficas. Puesto que no se
dan datos para tp, se puede hacer la suposición mas habitual tp=tg (aunque en el problema si se
hubiera puesto tp=0 también se habría dado por bueno).
La nueva envolvente compleja es: y c (t ) = Ac x(t − t g )e
− jωc t p
1.6. Calcular la relación señal ruido que se obtendría a la salida del sistema
total. ¿Cuál sería la snr si se hiciera el sistema en AM con una eficiencia de
potencia de 0.5?. (1 pto.)
Para calcular la relación señal-ruido hay que evaluar la fórmula de la snr a la salida del
sistema total, que en DBL es simplemente snr=prx/ηBx.
Para garantizar la calidad del sistema, hay que cumplir:
SNRo = Ptx [dBW ] − Acanal − 10 log10 η Bx = −3 − 80 − 10 log10 10−158103 = 27.96dB (=625)
Si el sistema fuera AM, la snr a la salida es snr=Ep prx/ηBx.
SNRo = Ptx [dBW ] − Acanal + 10 log10 E p − 10 log10 η Bx = −3 − 80 − 3 − 10 log10 10−158103 = 24.96dB
(=313)
Ingeniería de Telecomunicación, Escuela Politécnica Superior (UAM)
1