Geometría Analítica - Aprende Matemáticas

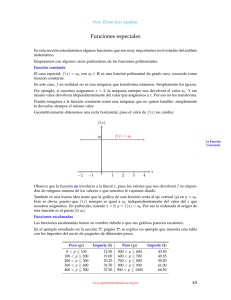
Profr. Efraín Soto Apolinar.
Circunferencia y secciones cónicas
El nombre «Secciones Cónicas» se derivó del hecho de que estas figuras se encontraron originalmente en un cono.
Cuando se hace intersectar un cono con un plano obtenemos distintas figuras. Cada una de ellas
es una cónica.
Cono
Un cono es el lugar geométrico que se forma al hacer girar una recta que pasa por el origen alrededor de
un eje. La recta que se hace girar siempre se considera distinta al eje y se conoce como generatriz.
z
tri
ra
e
n
Ge
Eje
O
Al cortar este cono con planos en diferentes posiciones obtenemos distintas figuras.
El corte para obtener una circunferencia se obtiene colocando el plano perpendicular al eje y,
obviamente que no pase por el origen del cono, porque en ese caso la intersección sería un punto.
Eje
O
Si el plano se coloca paralelo a una recta que se encuentre sobre el cono, de manera que lo corte,
obtenemos una parábola:
O
Eje
www.aprendematematicas.org.mx
1/3
Definición
1
Profr. Efraín Soto Apolinar.
Si el plano corta al cono en una de sus ramas y no es perpendicular al eje ni paralelo a una orilla
del cono, se forma una elipse:
O
Eje
Y si el plano corta ambas ramas del cono obtenemos una hipérbola:
O
Eje
Estos problemas pueden replantearse como la proporción entre las distancias desde un punto fijo
a una recta fija sobre el plano.
En estos casos, tenemos los siguientes planteamientos que originan los mismos lugares geométricos:
Parábola: Es el lugar geométrico de todos los puntos que equidistan de un punto fijo (llamado
foco) como de una recta fija (llamada directriz), ambos sobre el mismo plano.
Elipse: Es el lugar geométrico de todos los puntos que están k veces más alejados de una recta
fija (llamada directriz) que de un punto fijo (llamado foco).
Hipérbola: Es el lugar geométrico de todos los puntos que están k veces más cerca de una recta
fija (llamada directriz) que de un punto fijo (llamado foco).
De manera semejante, las dos últimas cónicas pueden definirse a partir de distancias medidas de
dos puntos fijos, que se denominan focos de la cónica.
Profesor:
Tarea
sugerida:
investigar y exponer por equipos
las
definiciones
de las cónicas
a partir de las
distancias a los
focos o a una
recta (parábola)
y ejemplos de
aplicación
de
cada una de ellas.
www.aprendematematicas.org.mx
2/3
Profr. Efraín Soto Apolinar.
Créditos
Albert
Einstein
Todo debe hacerse tan simple como sea posible, pero no más.
Este material se extrajo del libro Matemáticas I escrito por Efraín Soto Apolinar. La idea es compartir estos trucos para que más gente se enamore de las matemáticas, de ser posible, mucho más
que el autor.
Autor: Efraín Soto Apolinar.
Edición: Efraín Soto Apolinar.
Composición tipográfica: Efraín Soto Apolinar.
Diseño de figuras: Efraín Soto Apolinar.
Productor general: Efraín Soto Apolinar.
Año de edición: 2010
Año de publicación: Pendiente.
Última revisión: 31 de julio de 2010.
Derechos de autor: Todos los derechos reservados a favor de Efraín Soto Apolinar. México. 2010.
Espero que estos trucos se distribuyan entre profesores de matemáticas de todos los niveles y sean
divulgados entre otros profesores y sus alumnos.
Este material es de distribución gratuita.
Profesor, agradezco sus comentarios y sugerencias a la cuenta de correo electrónico:
efrain@aprendematematicas.org.mx
www.aprendematematicas.org.mx
3/3